Figures and data in Generating active T1 transitions through mechanochemical feedback

Figures
Tables
Additional files

8 figures, 2 tables and 1 additional file

Figures

Figure 1 with 2 supplements

Download asset Open asset

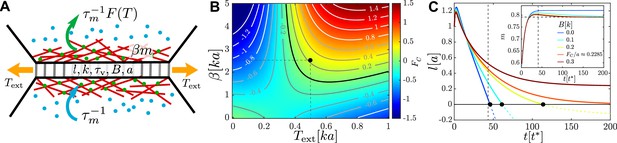
An active junction.

(A) An external pulling force of magnitude $T_{ext}$ induces tension $T$ in a cell–cell junction of length $l$ , which consists of passive viscoelastic and active components. The passive component consists of a Maxwell element with stiffness $k$ and viscous relaxation time $τ_{v}$ and a harmonic spring of stiffness $B$ and rest length $a$ connected to it in parallel. The active component is due to myosin motors (green and blue dots) with concentration $m$ that act to contract cortical actin filaments (red lines), exerting a force of magnitude $β m$ . Myosin motors bind to the actin cortex with association rate $τ_{m}^{- 1}$ and unbind with a tension-dependent dissociation rate $τ_{m}^{- 1} F (T)$ . (B) Heatmap plot of the contraction force $F_{C} (T_{e x t}, β)$ . For $B = 0$ , the junction contraction rate is $\dot{l} = F_{C} / ζ$ , where $ζ$ is the friction coefficient with the surrounding medium. The mechanochemical feedback loop is contractile in the top-right quadrant where $β > β_{c}$ , $T_{ext} > T^{*}$ , and $F_{C} > 0$ . Negative values of $F_{C}$ correspond to an extending junction. (C) Junction length vs. time for $T_{ext} = 0.5 k a$ , $β = 2.5 k a$ , $τ_{v} = τ_{m} = 10 t^{*}$ (black dot in B) for increasing values of the elastic barrier $B$ . An active $T 1$ corresponds to reaching $l = 0$ . Increasing $B$ slows down contractions, until, for $B \geq F_{C} / a$ , the equilibrium length $l \geq 0$ and no T1 is possible. Inset: myosin dynamics for the same set of junctions; the horizontal dashed line indicates $m_{eq} \cdot α = 1$ , $T^{*} = 0.3 k a$ , $k_{0} = 2 / T^{*}$ , and $m_{0} = 0.5$ . Length is measured in units of $a$ , time in units of $t^{*} = ζ / k$ , and force in units of $k a$ .

Figure 1—figure supplement 1

Download asset Open asset

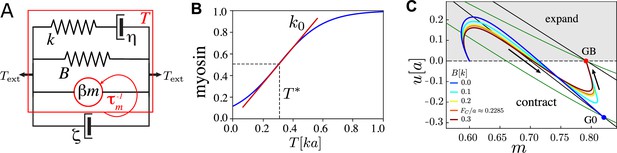
Key ingredients of the single active junction model.

(A) The junction is modelled as a Maxwell element with stiffness $k$ and viscosity $η$ (and the relaxation timescale $τ_{v} = η / k$ ) connected in parallel with the active forcing, and an elastic barrier with stiffness $B$ and rest length $a$ . It is coupled in parallel to a dashpot with viscosity $ζ$ modelling dissipation with the surrounding medium. The red arrow indicates the feedback loop between tension and myosin kinetics. (B) Myosin–tension response curve, for $F (T) = α + e^{- k_{0} (T - T^{*})}$ with $α = 1$ , $T^{*} = 0.3 k a$ , $k_{0} = 2 / T^{*}$ , $m_{0} = 0.5$ . (C) Trajectories in the $u - m$ plane for several values of $B$ , where $u = l - l_{0}$ . G0 (GB) is the fixed point with no ( $B > 0$ ) elastic barrier. Fixed points are located at the intersection of their respective $u$ (black) and $m$ (green) nullclines. Arrows indicate the direction of motion. $α = 1$ , $T^{*} = 0.3 k a$ , $k_{0} = 2 / T^{*}$ , and $m_{0} = 0.5$ . Length is measured in units of $a$ , time in units $t^{*} = ζ / k$ , and force in units of $k a$ .

Figure 1—figure supplement 2

Download asset Open asset

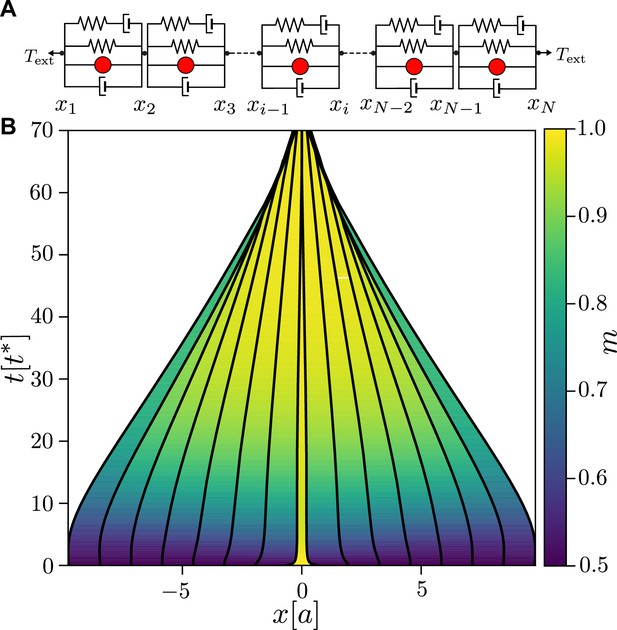
A linear chain of active junctions.

(A) Schematic of a linear chain for viscoelastic junctions with active tension feedback. The chain is formed by connecting in series the active viscoelastic elements shown in Figure 1—figure supplement 1A, with the pulling force of magnitude $T_{ext}$ applied to both ends. (B) Time evolution of a linear chain for $T_{ext} = 0.385 k a$ and $β = 2.5 k a$ with an initial pulse of myosin. The central contraction propagates rapidly outwards, resulting in a contraction and collapse of the chain. Activity and pulling force correspond to a point on the contraction–extension separatrix in Figure 1B, putting the system in a mechanically neutral state. The remaining parameters are the same as in Figure 1C.

Figure 2 with 14 supplements

Download asset Open asset

An active T1 transition event.

(A) Top panel: the mechanical anisotropy in the initial state is produced by applying pulling forces (green arrows) in the horizontal direction to the left and right boundaries. Bottom panel: the final state after the active T1 shows a clear convergence–extension deformation (red arrows). Cells are coloured by type: passive (light grey), buffer (medium grey), and active (dark grey). Junctions are coloured by junctional myosin. (B) Time sequence of the active T1 transition measured from the moment activity and viscoelasticity were switched on. Cells in the top row are coloured by type and junctions are coloured by tension. Cells in the bottom row are coloured by activated myosin $m_{act}^{C}$ , and junctions are coloured by myosin. Parameters: $A_{0} = \frac{3}{2} \sqrt{3} a^{2}$ , $P_{0} = 6 a$ , $β = 0.8 f^{*}$ (active), $β = 0.4 f^{*}$ (buffer), $β = 0$ (passive), $M = 6$ , $T^{*} = 0.3 f^{*}$ , $k_{0} = 2 / T^{*}$ , $τ_{v} = 20 t^{*}$ , $τ_{m} = 100 t^{*}$ , $α = 0.1$ , $f = 1$ , $f_{pull} = 0.15 f^{*}$ , with $n_{x} = 15$ ( $n_{y} = 11$ ) cells in the horizontal (vertical) direction. Units: length ( $a$ ), time ( $t^{*} = ζ / (Γ + k)$ ), force ( $f^{*} = (Γ + k) a$ ).

Figure 2—figure supplement 1

Download asset Open asset

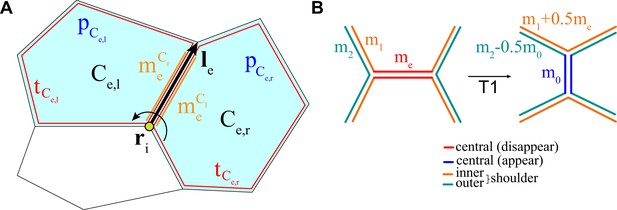
Schematic representation of the key ingredients in the vertex model with active junctions.

(A) The total force on vertex i can be expressed as a sum of forces due to junctions. For the junction $e$ , $C_{e, l}$ and $C_{e, r}$ are the cells to the left and the right, respectively, when looking in the direction of the vector $l_{e} \cdot m_{e}^{C_{1}} (m_{e}^{C_{r}})$ is the myosin attached to junction e due to the cell to the left (right) of it. The area ( $p_{C_{e, l / r}}$ ) and perimeter ( $t_{C_{e, l / r}}$ ) terms are defined in the text above. (B) Example of the redistribution of myosin after a T1 transition for one side of the junction, and one of its inner and outer shoulder junctions.

Figure 2—video 1

Download asset

posterframe for video — Simulation of a passive system with applied horizontal pulling for $f_{pull} = 0.15 f^{*}$ .

Left panel - junction and cell myosin; right panel - junction tension, cells are coloured by type, active (dark grey), buffer (intermediate grey), passive (light grey). In this video activity is turned off, and there is no difference between those three cell types.

Figure 2—video 2

Download asset

Figure 2—video 3

Download asset

Figure 2—video 4

Download asset

Figure 2—video 5

Download asset

Figure 2—video 6

Download asset

Figure 2—video 7

Download asset

Figure 2—video 8

Download asset

Figure 2—video 9

Download asset

Figure 2—video 10

Download asset

Figure 2—video 11

Download asset

Figure 2—video 12

Download asset

Figure 2—video 13

Download asset

Figure 3 with 1 supplement

Download asset Open asset

Junction dynamics during the active T1 transition shown in Figure 2.

(A) Definition of central (red/blue – junction that disappears/appears), inner (orange), and outer (blue-green) shoulder junctions through the T1 transition. (B) Central junction: myosin, $m$ (green; two curves for myosin on two sides of the junction), tension, $T$ (yellow), junction length, $l$ (black), and rest length l₀ (purple) vs. time. The vertical line indicates the T1 transition, at which point junctional myosin is redistributed according to the rules outlined in Figure 2—figure supplement 1B. (C) Same as in panel (A) but averaged over four shoulder junctions, with variance indicated as shade. (D) Polar histogram of the orientation of the first T1 event measured with respect to the pulling direction, from $n = 32$ simulations. Blue (red) indicates appearing (disappearing) junctions. Parameters are $β = 0.8 f^{*}$ and $f_{pull} = 0.15 f^{*}$ and as in Figure 2.

Figure 3—figure supplement 1

Download asset Open asset

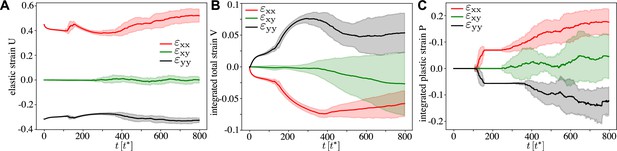
Continuous strain tensors through the active T1 transition, for $β = 0.8 f^{*}$ , $f_{pull} = 0.15 f^{*}$ , and the other parameters corresponding to Figure 2 and Figure 3.

(A) Statistical strain tensor $\hat{U}$ defined in Equation 20, with the initial undeformed state used as reference configuration. (B) Total strain, that is, integrated $\hat{V}$ tensor defined in Equation 24. (C) Integrated plastic strain tensor $\hat{P}$ defined in Equation 22. One can see that the active T1 proceeds at near constant elastic strain with cells elongated in the pulling direction, that is, $ε_{x x} > 0$ and $ε_{yy} < 0$ . Conversely, there is clear convergence–extension since $ε_{xx} < 0$ and $ε_{yy} > 0$ in the total strain. Here, the traces are an average over $n = 32$ simulations, and the shading corresponds to the error of the mean.

Figure 4

Download asset Open asset

Existence and timescales of T1 transitions in the vertex model with active junctions as a function of $f_{pull}$ and $β$ , averaged over $n = 32$ simulations with different realisations of the myosin noise.

(A) Probability of a central T1 transition. The red line is the 50% probability contour of any T1 occurring in the simulation. (B) Typical timescale for the T1 transition to occur, measured as the length of the contraction phase. The other parameters are the same as in Figure 2. (C) Magnitude of the convergence–extension deformation as a function of $f_{pull}$ and characterised by measuring $ε_{xx}^{tot} - ε_{yy}^{tot}$ induced by the T1 transition.

Figure 5

Download asset Open asset

Robustness of the T1 mechanism as a function of $τ_{v}$ and $τ_{m}$ for $β = 1.0 f^{*}$ and $f_{pull} = 0.15 f^{*}$ .

(A) Probability of a central T1 event, averaged over $n = 32$ simulations with different realisations of the myosin noise. The probability of any T1 event is 1 throughout. (B) Contraction time to collapse for the central T1 as a function of $τ_{v}$ , for different values of $τ_{m}$ , for points where a central T1 event occurred in at least 25% of simulations. (C) Peak of the total convergence extension strain $ε_{xx}^{tot} - ε_{yy}^{tot}$ , showing very weak dependence on viscoelastic and myosin timescales. Shading in panels (B) and (C) indicates the standard error of the mean.

Figure 6 with 2 supplements

Download asset Open asset

Disordered active tissue at time $t \approx 700 t^{*}$ as a function of the magnitude of the pulling force $f_{pull}$ and activity $β$ .

The region of convergence–extension is at the centre of the diagram, around $β \approx 0.4 - 0.6 f^{*}$ and $f_{pull} \approx 0.1 - 0.3 f^{*}$ . The remaining parameters are the same as in Figure 2.

Figure 6—video 1

Download asset

Figure 6—video 2

Download asset

Figure 7 with 3 supplements

Download asset Open asset

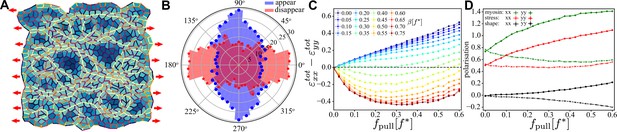
Characterisation of convergence-extension in a random tissue patch.

(A) Snapshot of a random tissue patch for $β = 0.5 f^{*}$ and $f_{pull} = 0.2 f^{*}$ at $t \approx 700 t^{*}$ ,that is during the convergence–extension flow. Red arrow indicates that a constant pulling force is applied throughout the entire simulation. (B) Angular histogram of T1 events for same values of $β$ and $f_{pull}$ . Cells and junctions are coloured as in Figure 6. (C) Magnitude of the convergence–extension deformation as a function of $f_{pull}$ characterised by measuring $ϵ_{x x}^{tot} - ϵ_{y y}^{tot}$ induced by the T1 transition. (D) Anisotropy along ( $x x$ , solid line) and perpendicular to ( $y y$ , dashed line) the direction of the external pulling force for myosin (green), mechanical stress (red), and shape tensor (black) as functions of $f_{pull}$ for $β = 0.5 f^{*}$ at $t \approx 700 t^{*}$ . In (C) and (D), each point was averaged over $n = 33$ independent samples and the error bar is smaller than the symbol size.

Figure 7—figure supplement 1

Download asset Open asset

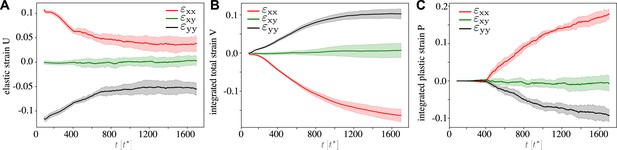
Continuous strain tensors for the fully active tissue at $β = 0.5 f^{*}$ , $f_{pull} = 0.2 f^{*}$ , and the other parameters corresponding to Figure 2 and Figure 3.

(A) Statistical strain tensor $\hat{U}$ defined in Equation 20, with the initial undeformed state used as reference configuration. (B) Total strain, that is, integrated $\hat{V}$ tensor defined in Equation 24. (C) Integrated plastic strain tensor $\hat{P}$ defined in Equation 22. Convergence–extension flow proceeds with cells elongated in the pulling direction, that is, $ε_{xx} > 0$ and $ε_{yy} < 0$ while $ε_{xx} < 0$ and $ε_{yy} > 0$ in the total strain. Here, the traces are an average over $n = 5$ simulations, and the shading corresponds to the standard deviation.

Figure 7—figure supplement 2

Download asset Open asset

Measuring T1 transitions in the fully active random patch.

A representative example taken from a sample of $n = 5$ simulations for $β = 0.5 f^{*}$ , $f_{pull} = 0.2 f^{*}$ . (A) Appearing and disappearing junctions as a function of simulation frame number and angle, before filtering. Inset: raw T1 histogram. (B) Same dataset after filtering procedure.

Figure 7—figure supplement 3

Download asset Open asset

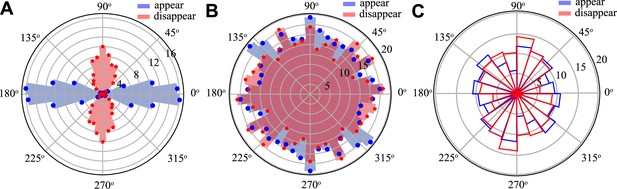
T1 histograms in the parameter range where no convergence–extension occurs.

(A) Passive tissue at $β = 0$ pulled with $f_{pull} = 0.2 f^{*}$ , T1s are passive and aligned along pulling direction. (B) Active tissue at $β = 0.5 f^{*}$ with no applied force $f_{pull} = 0.0 f^{*}$ , here T1s are distributed isotropically. (C) Experimental T1 distribution in the anterior region of the streak, strongly resembling the active isotropic case.

Figure 8 with 3 supplements

Download asset Open asset

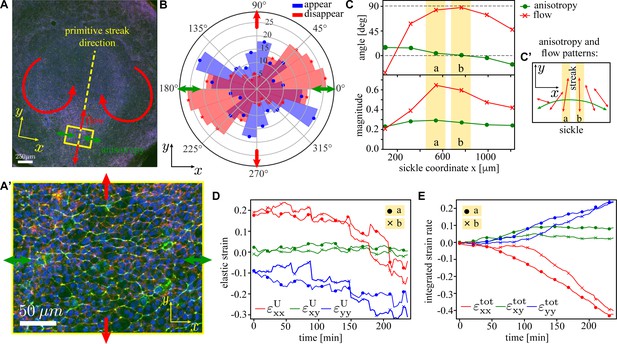
Analysis of the tissue flows in the early-stage chick embryo.

(A) Image of a typical early-stage chick embryo prior to the gastrulation (i.e. primitive streak formation). The primitive streak will form along the yellow dashed line. The direction of myosin anisotropy is shown by the green double-headed arrows, and the direction of the tissue flow is indicated by the red arrows. x-axis is chosen to coincide with the long direction of the sickle-shaped active region in the embryo’s posterior (Rozbicki et al., 2015). (A’) Zoom-in of the rectangular region on the posterior side of the embryo; myosin II (green), actin (red), and nuclei (blue). (B) Measured distribution of the orientation of T1 events in a circular patch of diameter ≈ 190 $μ m$ tracked over the period of ≈ 6 hr (cf. model distribution in Figure 7B). Blue (red) denotes junctions that appear (disappear); arrows have the same meaning as in (A). (C) Angle (red) and magnitude (green) of tissue shape anisotropy (dots) and tissue flow (crosses) for $n = 6$ rectangular patches along the sickle with corresponding anisotropy and flow patterns shown in (C’). Components of the elastic strain tensor $\hat{U}$ (D) and the total integrated strain tensor $\hat{V}$ (E; definition in Equation 24) as a function of time during first 4 hr of the streak formation for two central regions of the sickle (yellow stripes in C). Details of the analysis are given in ‘Materials and methods’.

Figure 8—figure supplement 1

Download asset Open asset

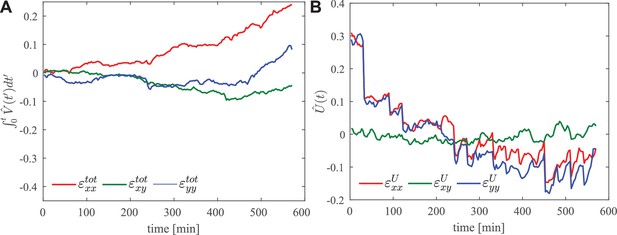
Region of interest in the anterior of the embryo.

(A) Integrated total strain ${\hat{ε}}^{tot} (t)$ and (B) elastic strain $\hat{U} (t)$ .

Figure 8—video 1

Download asset

Figure 8—video 2

Download asset

Tables

Table 1

Values of the parameters in the single-junction model.

Units: length ( $a$ ), time ( $t^{*} = ζ / k$ ), force ( $k a$ ).

Base
Parameter	Description
$k$	Spring constant
$a$	Barrier rest length
$ζ$	Friction with substrate
Model
Parameter	Description	Value range
$B$	Barrier spring constant	$0 - 0.2 k$
$T_{ext}$	Applied external tension	$0 - 1 k a$
$β$	Myosin activity	$0 - 3 k a$
$τ_{v}$	Viscoelastic time	$10 t^{*}$
$τ_{m}$	Myosin time	$10 t^{*}$
$m_{0}$	Myosin reference level	0.5
$T^{*}$	Threshold tension	$0.3 k a$
$k_{0}$	Slope of $m$ vs. $T$ at $T^{*}$	$2 / T^{*}$
$α$	Tension-independent myosin dissociation	1

Table 2

Values of the parameters used in the vertex model with active junctions.

Units: length ( $a$ ), time ( $t^{*} = ζ / (Γ + k)$ ), force ( $f^{*} = (Γ + k) a$ ).

Base
Parameter	Description
$a$	Hexagonal cell edge length
$Γ$	Perimeter modulus
$k$	Spring constant
$ζ$	Friction with substrate
Model
Parameter	Description	Value range
$κ$	Area modulus	$1 f^{*} / a^{3}$
$A_{0}$	Target cell area	$3 \sqrt{3} a^{2} / 2$
$P_{0}$	Target cell perimeter	$6 a$
$f_{pull}$	Pulling force	$0.0 - 0.3 f^{*}$
$β$	Myosin activity	$0.0 - 1.4 f^{*}$
$τ_{v}$	Viscoelastic time	$10^{0} - 10^{3} t^{*}$
$τ_{m}$	Myosin time	$10^{1} - 10^{3} t^{*}$
$T^{*}$	Threshold tension	$0.3 f^{*}$
$K_{0}$	Slope of $m$ vs. $T$ at $T^{*}$	$2 / T^{*}$
$m_{0}$	Myosin reference level	0.5
$M$	Total cell myosin	6
$f$	Variance of myosin fluctuations	1
$α$	Tension-independent myosin dissociation	0.1

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/79862/elife-79862-mdarchecklist1-v3.pdf
Download elife-79862-mdarchecklist1-v3.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Rastko Sknepnek
Ilyas Djafer-Cherif
Manli Chuai
Cornelis Weijer
Silke Henkes

(2023)

Generating active T1 transitions through mechanochemical feedback

eLife 12:e79862.

https://doi.org/10.7554/eLife.79862

Share this article

Cite this article

An active junction.

Key ingredients of the single active junction model.

A linear chain of active junctions.

An active T1 transition event.

Schematic representation of the key ingredients in the vertex model with active junctions.

Simulation of a passive system with applied horizontal pulling for fpull=0.15⁢f*.

Low activity system with no T1 transitions.

Active T1 transition.

System with low pulling force.

System with too high pulling force.

System with too high activity.

Active T1 transition with low τm and τv.

Active T1 transition with low τm.

Active T1 transition with low τv.

Active T1 transition at intermediate values of τm and τv.

Active T1 transition at high τv.

Active T1 transition at high τm.

Active T1 transition at high τm and τv.

Junction dynamics during the active T1 transition shown in Figure 2.

Continuous strain tensors through the active T1 transition, for β=0.8⁢f*, fpull=0.15⁢f*, and the other parameters corresponding to Figure 2 and Figure 3.

Existence and timescales of T1 transitions in the vertex model with active junctions as a function of fpull and β, averaged over n=32 simulations with different realisations of the myosin noise.

Robustness of the T1 mechanism as a function of τv and τm for β=1.0⁢f* and fpull=0.15⁢f*.

Disordered active tissue at time t≈700⁢t* as a function of the magnitude of the pulling force fpull and activity β.

Video of simulations of active contractions in disordered tissues for a range of activities, β, and magnitudes of the pulling force, fpull.

Active T1 transitons in a random patch.

Characterisation of convergence-extension in a random tissue patch.

Continuous strain tensors for the fully active tissue at β=0.5⁢f*, fpull=0.2⁢f*, and the other parameters corresponding to Figure 2 and Figure 3.

Measuring T1 transitions in the fully active random patch.

T1 histograms in the parameter range where no convergence–extension occurs.

Analysis of the tissue flows in the early-stage chick embryo.

Region of interest in the anterior of the embryo.

Image sequence taken at the base of the forming streak showing cell intercalations.

Image sequence taken in the region of epiblast in front of forming streak.

Values of the parameters in the single-junction model.

Values of the parameters used in the vertex model with active junctions.

MDAR checklist

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Simulation of a passive system with applied horizontal pulling for $f_{pull} = 0.15 f^{*}$ .

Active T1 transition with low $τ_{m}$ and $τ_{v}$ .

Active T1 transition with low $τ_{m}$ .

Active T1 transition with low $τ_{v}$ .

Active T1 transition at intermediate values of $τ_{m}$ and $τ_{v}$ .

Active T1 transition at high $τ_{v}$ .

Active T1 transition at high $τ_{m}$ .

Active T1 transition at high $τ_{m}$ and $τ_{v}$ .

Continuous strain tensors through the active T1 transition, for $β = 0.8 f^{}$ , $f_{pull} = 0.15 f^{}$ , and the other parameters corresponding to Figure 2 and Figure 3.

Existence and timescales of T1 transitions in the vertex model with active junctions as a function of $f_{pull}$ and $β$ , averaged over $n = 32$ simulations with different realisations of the myosin noise.

Robustness of the T1 mechanism as a function of $τ_{v}$ and $τ_{m}$ for $β = 1.0 f^{}$ and $f_{pull} = 0.15 f^{}$ .

Disordered active tissue at time $t \approx 700 t^{*}$ as a function of the magnitude of the pulling force $f_{pull}$ and activity $β$ .

Video of simulations of active contractions in disordered tissues for a range of activities, β, and magnitudes of the pulling force, $f_{pull}$ .

Continuous strain tensors for the fully active tissue at $β = 0.5 f^{}$ , $f_{pull} = 0.2 f^{}$ , and the other parameters corresponding to Figure 2 and Figure 3.