Figures and data in Evolution of cell size control is canalized towards adders or sizers by cell cycle structure and selective pressures

Version of Record

Accepted for publication after peer review and revision.

Download
Cite
Share
CommentOpen annotations (there are currently 0 annotations on this page).

Version of Record published: November 11, 2022 (This version)
Accepted Manuscript published: September 30, 2022 (Go to version)
Accepted: September 25, 2022
Received: May 2, 2022
Preprint posted: April 13, 2022 (Go to version)

Figures
Tables
Additional files

17 figures, 8 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

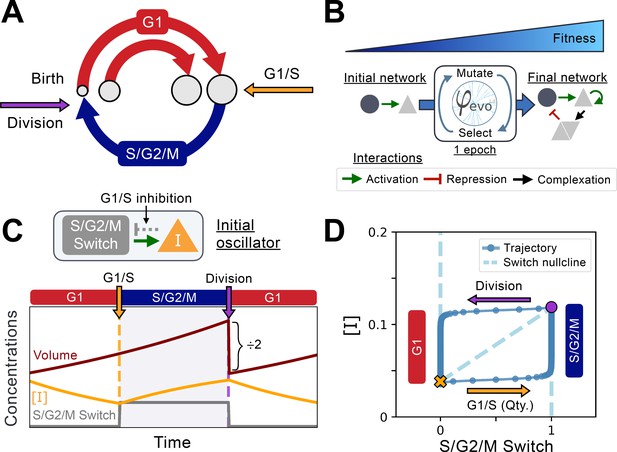
Implementation of the cell cycle seed network and evolution algorithm.

(A) Schematic representation of the coupling between cell size and cell cycle progression. The transition between G1 (red) and S phases of the cell cycle at the G1/S transition (orange) can evolve to depend on cell size, while the duration of the S/G2/M (blue) phase is independent of size. Cell division takes place instantaneously following mitosis (purple). (B) Schematic representation of the φ-evo algorithm implementation. The network generating tool takes an initial network topology as its starting point for evolution as well as a user-defined fitness function. φ-evo then goes through successive epochs of mutation and selection to extract a final optimized network. At each selection step, the fittest half of the networks are retained and duplicated for evolution in the subsequent epoch. Interactions permitted to be mutated by φ-evo include transcriptional activation (green arrow), transcriptional repression (red arrow) and protein-protein interactions responsible for complex formation (black arrow). (C) Schematic of our seed network topology implementing a simplified relaxation oscillator. Cell cycle state (G1 or S/G2/M) is encoded via a binary switch called *‘S/G2/M Switch’* that is 0 in G1 and 1 in S/G2/M. Transition between G1 and S is controlled by the quantity of an inhibitor of the G1/S transition that we call $I$ . The lower the quantity $I$ , the higher the chance of progression through the G1/S transition. This interaction is represented as the grey arrow in the network topology and cannot be mutated by φ-evo. After progressing through G1/S, cells enter S/G2/M which we model as a pure timer of fixed duration with some uniform noise. Cell volume grows exponentially and is divided symmetrically following mitosis. We then follow one of the daughter cells and disregard the other one. (D) Phase-space representation of the initial relaxation oscillator. The X-coordinate shows the S/G2/M Switch variable, and the Y-coordinate shows the concentration of $[I]$ . The oscillator runs counterclockwise with the left branch (x=0) corresponding to G1 and the right branch (x=1) corresponding to S/G2/M. The G1/S transition and division events are instantaneous in our simulations but are smoothly represented here for visualization purposes. From these transitions, we can extract the approximate shape of the $[I]$ nullcline that we plot under the oscillator with a dashed line. We note that the position of the G1/S transition in phase-space will vary as a function of the volume of the cell as it depends on the *quantity* of $I$ rather than its *concentration* $[I]$ .

Figure 2

Download asset Open asset

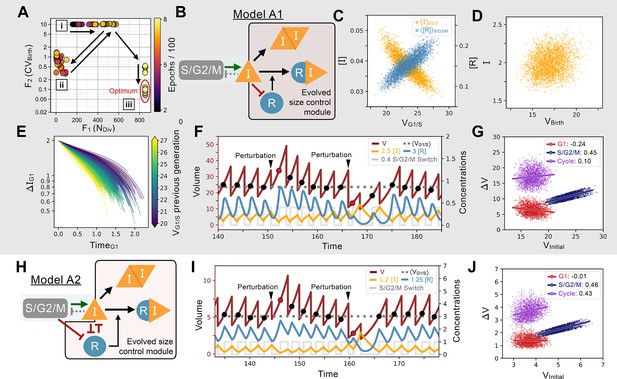
Evolution of feedback-based size control.

(A) Typical 2D fitness trajectory for an evolutionary run. Individual networks are dots color coded by their epoch within the evolutionary trajectory. Fitness function of the number of divisions of a cell lineage during a time interval of fixed length ( $F_{1} (N_{D i v})$ , X-coordinate) and fitness function of the coefficient of variation of the volume distribution at birth ( $F_{2} (C V_{B i r t h})$ , Y-coordinate). Optimal model behavior is located in the bottom right corner of the figure where networks produce cell lineages with many offspring and strong size control. First, there are several epochs without any size control; networks cluster in two regions of the Pareto front corresponding to volume going to the maximum allowed value (cluster [i]) or to the minimum value (cluster [ii]). Both cases are highly penalized in their fitness score. Evolution goes back and forth between the [i] and [ii] clusters with a slow increase in the number of divisions (X-coordinate). Eventually, some volume control evolves and networks transition in the [iii] cluster where their $C V_{B i r t h}$ is slowly optimized further until the end of the run. (B) Core network topology of the evolved Model A1 network that employs a feedback-based mechanism described in detail in panels C-F. (C) Concentration of $[I]$ at the G1/S transition (Y-coordinate, left axis, orange) and average concentration of the repressor protein $[R]$ in S/G2/M (Y-coordinate, right axis, light blue) as a function of the volume of the cell at G1/S (X-coordinate), that is, the beginning of S phase. We see here that $[R]$ acts as a direct size sensor of the volume at G1/S. (D) *Quantity* of inhibitor $I$ at birth as a function of volume of the cell at birth, which is independent of size due to titration by $[R]$ during S/G2/M. (E) Trajectories of quantity of inhibitor $I$ in G1 as a function of time. Trajectories are color coded as a function of the volume at G1/S during the previous generation’s cell cycle. For visualization purposes, trajectories are offset vertically to all begin at the average *quantity* of $I$ at birth (t=0) shown to be on average independent of volume in panel D. Larger cell volumes lead to greater titration of $[I]$ in G1 by $[R]$ . In turn, this ensures that G1 duration of the daughter cell cycle is shorter, which underpins the size control mechanism. (F) Characteristic dynamics of Model A1. Circles indicate volume at G1/S. Extrinsic perturbations are applied to the model by temporarily changing the division ratios which kicks the system out of equilibrium at the subsequent cycle such that $V_{N e x t G 1 / S}^{} = (1 \pm 0.5) ⟨ V_{G 1 / S} ⟩$ . The volume relaxation back to its homeostatic value takes ~2–3 generations, almost insensitive to the fact that the perturbation is applied towards higher or lower volumes. (G) Amount of volume added $Δ V$ in G1 (red), S/G2/M (dark blue), and over the whole cycle (purple) as a function of their initial volume at the beginning of these phases, *that is,* birth for G1 and cycle, and G1/S for S/G2/M, with the slope of linear fits indicated in legend. Slope of 1 corresponds to a Timer, slope of –1 to a Sizer and slope of 0 to an Adder. (H) Network topology of Model A2, a second evolved network that is similar to Model A1 albeit with different kinetic parameters and 2 additional interactions (see text). (I) Characteristic dynamics of Model A2. Extrinsic perturbations are applied like in (F). The volume relaxation back to its homeostatic value takes ~3–4 generations when applied towards the higher volumes but only 1 generation when applied towards the lower volumes. (J) Amount of volume added for different periods of the cell cycle for Model A2.

Figure 3

Download asset Open asset

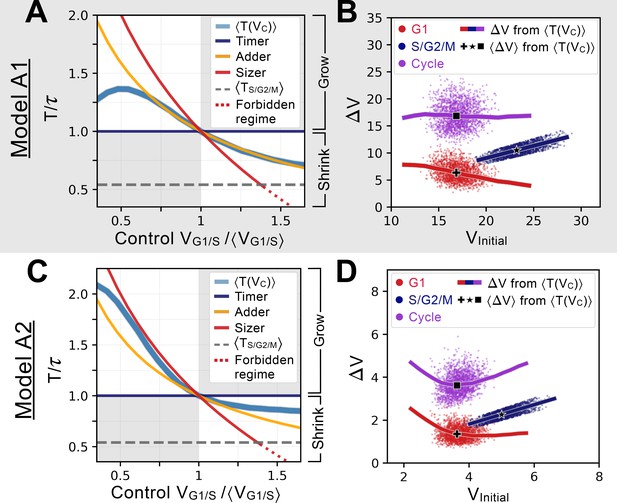
Characterizing and comparing evolved size control mechanisms.

(A) Average period $T (V_{C})$ of the oscillator of Model A1 as a function of the control volume $V_{C}$ at the G1/S transition. Period is normalized by $τ$ the doubling time of the cell, and volume is rescaled by $⟨ V_{G 1 / S} ⟩$ , which corresponds to $T (⟨ V_{G 1 / S} ⟩) = τ$ . Normalized periods larger than 1 indicate cell lineages that grow over time whereas normalized periods smaller than 1 indicate lineages that shrink over time. Periods for the sizer (red), adder (orange) and timer (dark blue) are shown for comparison. The S/G2/M timer period is incompressible and prevents a perfect sizer from existing in the large volume range as indicated by the red dotted line. Model A1 follows approximately the adder archetype over a large range of control volumes. (B) Added volumes $Δ V$ for different phases of the cell cycles for simulations of Model A1. Individual dots correspond to different cell cycles for a simulation at steady-state. The full line corresponds to the extrapolation from the $T (V_{C})$ curve shown in A for a restricted range of $V_{C}$ relevant to the scatter. The black cross, star and square indicate the average added volumes corresponding to when the system senses a volume corresponding to $⟨ V_{G 1 / S} ⟩$ at the G1/S transition. We see that the model is predicted to follow an adder over a large range of volumes. (C) Average period $T (V_{C})$ of the oscillator of Model A2, with similar conventions as for panel A. We note that the $T (V_{C})$ curve of this model is closer to the sizer at lower volumes and closer to a weak adder/timer at higher volumes relative to $⟨ V_{G 1 / S} ⟩$ . (D) Added volumes $Δ V$ for different phases of the cell cycles for simulations of Model A2, with similar conventions as for panel B. Here we see the predicted sizer behavior at lower volumes and the weak adder/timer behavior at higher volumes.

Figure 4

Download asset Open asset

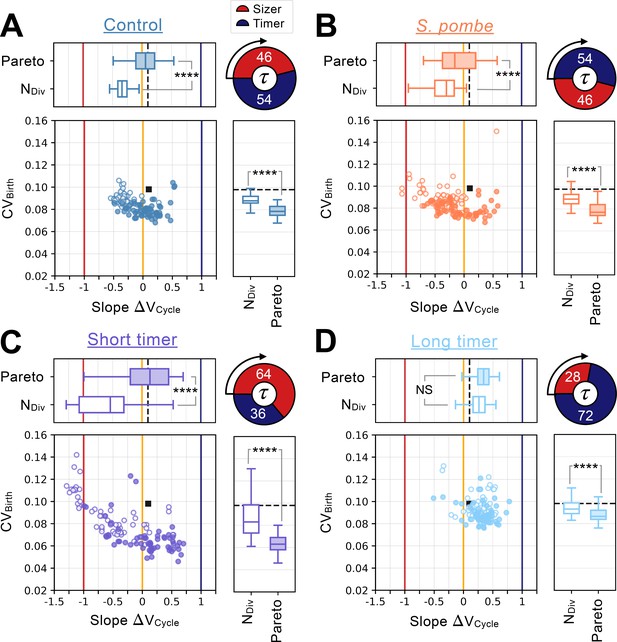
Distinct network constraints and selection pressures bias size control evolution towards adders or sizers.

Summary statistics for evolutionary simulations each having 500 epochs. Model A1 shown in Figure 2A-G was used as the initial seed network. 60 simulations were performed using Pareto optimization of the number of divisions ( $N_{D i v}$ ) and the CV of cell size at birth ( $C V_{B i r t h}$ ), are labeled *Pareto* and are shown in full colors. 60 more simulations were performed using only the number of divisions as the fitness function, are labeled *N_Div* and are shown in colored outlines only. Scatter plots show the coefficient of variation of the size distribution at birth ( $C V_{B i r t h}$ , Y-coordinate) as a function of the fitted added volume slope over the whole cycle as a function of volume at birth (Slope $Δ V_{C y c l e}$ , X-coordinate) for the most fit models evolved during each of the 120 independent simulations. Horizontal box plots above the scatter plots display the distributions of the added volume slopes for the *Pareto* and *N_Div* simulations. Timer (dark blue), adder (orange) and sizer (red) slopes are shown respectively at 1, 0, and –1 for comparison. Vertical box plots on the right of the scatter plots show the distributions of $C V_{B i r t h}$ for the *Pareto* and *N_Div* simulations. Asterisks represent p-values for the Welch’s t-Test between the distributions. For reference, $N S$ indicates $p > 0.05$ , * indicates $p < 0.05$ , ** indicates $p < 10^{- 2}$ , *** indicates $p < 10^{- 3}$ and **** indicates $p < 10^{- 4}$ . The values of $C V_{B i r t h}$ and Slope $Δ V_{C y c l e}$ for the initial seed Model A1 are shown as a black square in the scatter plot or as a dashed black line in the box plots. Each panel explores different cell cycle structures which are summarized by the pie charts. Cycles begin on the left of the pie charts and rotate clockwise, indicating the order of the sizer (red) and timer (dark blue) phases. The labels indicate each phase’s duration at equilibrium as a percentage of the doubling time $τ$ . (A) Identical evolutionary parameters as for Model A1 evolution shown in Figure 2A–G. G1 performs size control and has a duration $0.46 τ$ at equilibrium and S/G2/M is a timer of duration $0.54 τ$ . (B) Evolution results for a cell cycle structure where the sizer and the timer phases of the cell cycle are inverted akin to *S. pombe*. G1 is a timer of duration $0.54 τ$ and S/G2/M performs size control and has duration $0.46 τ$ at equilibrium. (C) Evolution results for a G1 size control of average duration $0.64 τ$ at equilibrium where S/G2/M is a timer of duration $0.36 τ$ . (D) Evolution results for a G1 size control of average duration $0.28 τ$ at equilibrium where S/G2/M is a timer of duration $0.72 τ$ .

Figure 5

Download asset Open asset

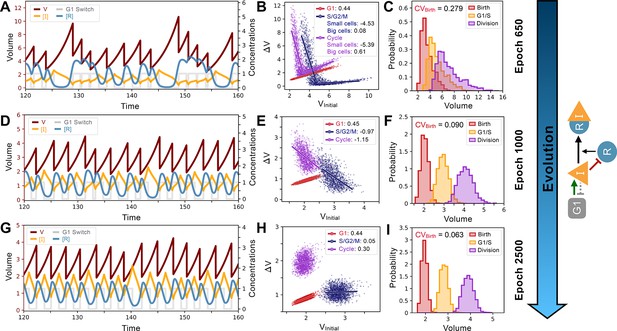
System and evolutionary dynamics of cell size control networks.

Snapshots of an evolutionary simulation of 2500 epochs initialized with the Model A1 network topology along with an *S. pombe*-like cell cycle structure with a timer in G1 followed by a sizer in S/G2/M (see Figure 4B). Pareto fitness optimization was performed using $N_{D i v}$ and $C V_{B i r t h}$ as fitness functions. Rows indicate simulation results for the fittest networks from evolutionary epochs 650 (Panels A-C), 1000 (Panels D-F), and 2500 (Panels G-I). Network topology remains the same throughout the evolutionary simulation and is shown on the right. Evolutionary dynamics continually reduce the selected for $C V_{B i r t h}$ and proceed through a noisy sizer to a less noisy adder. (A) Typical dynamics of the most fit model from epoch 650. (B) Added volumes $Δ V$ for different phases of the cell cycle for the most fit model from epoch 650. Fitted slopes are indicated in the legend. Fits for the S/G2/M and Cycle added volumes were split in two separate the size control for small and large cells. (C) Size distributions at birth (red), G1/S (orange), and division (purple) for the most fit model from epoch 650. The coefficient of variation of the volume distribution at birth $C V_{B i r t h} = 0.279$ . (D) Typical dynamics of the most fit model from epoch 1000. (E) Added volumes $Δ V$ for different phases of the cell cycle for the most fit model from epoch 1000. Fitted slopes are indicated in the legend. (F) Size distributions at birth (red), G1/S (orange), and division (purple) for the most fit model from epoch 1000. The coefficient of variation of the volume distribution at birth $C V_{B i r t h} = 0.090$ . (G) Typical dynamics of the most fit model from epoch 2500. (H) Added volumes $Δ V$ for different phases of the cell cycle for the most fit model from epoch 2500. Fitted slopes are indicated in the legend. (I) Size distributions at birth (red), G1/S (orange), and division (purple) for the most fit model from epoch 2500. We see here that the sizer behavior from epoch 1000 was abandoned for a weaker adder overall yielding lower $C V_{B i r t h} = 0.063$ .

Figure 6

Download asset Open asset

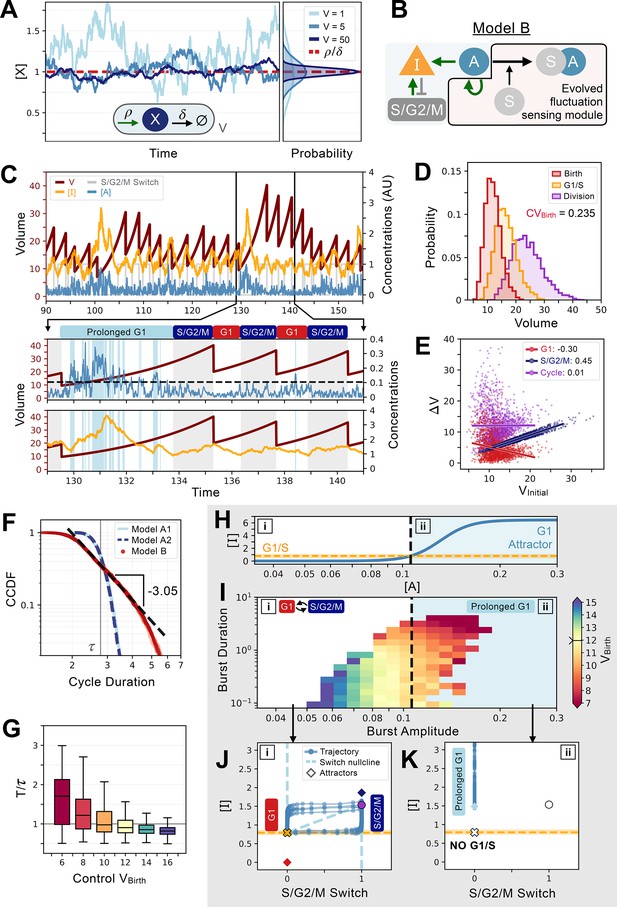
An evolved concentration fluctuation sensing size control model exhibits self-organized criticality.

(A) Size-dependent molecular noise arises due to Poissonian fluctuations in molecule number. Consider a protein production-degradation scheme for protein *quantity X* with production rate $ρ$ and degradation rate $δ$ contained in a volume V. At equilibrium, the concentration of $[X]$ will be given by a distribution with mean $\frac{ρ}{δ}$ and variance $\propto \frac{1}{V}$ . The effect of V on the molecular noise is shown on the time trajectories for simulations in a constant volume of V=1 (light blue), V=5 (medium blue), and V=50 (dark blue). Corresponding concentration distributions are shown on the right-hand side of the panel. (B) Network topology of Model B which evolved to sense fluctuations. Here, the G1/S transition is controlled by the *concentration* of $[I]$ and not its *quantity*. (C) Characteristic cell cycle dynamics of Model B. Trajectories of $[I]$ , $[A]$ , and S/G2/M Switch are rescaled with arbitrary units (AU) for visualization purposes. Below, we zoom-in on three cycles to show how a low-volume induced burst in $[A]$ leads to a massive production of $[I]$ inducing a temporarily prolonged G1 phase. Subsequently, cells become bigger and display lower molecular noise inducing a comparatively shorter G1 phase. (D) Volume distributions at birth (red), G1/S (orange), and division (purple) for Model B. The coefficient of variation of the volume distribution at birth $C V_{B i r t h} = 0.235$ . (E) Amount of volume added $Δ V$ in G1 (red), S/G2/M (dark blue), and over the whole cycle (purple) as a function of their initial volume at the beginning of these phases, *i.e.,* birth for G1 and cycle, and G1/S for S/G2/M, with the slope of linear fits indicated in legend. (F) Complementary cumulative distribution functions of the cycle duration (CCDF; probability that the cell cycle duration is larger than the value on the X-axis) for three models discussed in the main text: Model A1 (light blue), Model A2 (dashed dark blue), and Model B (red). The light grey line indicates the doubling time $τ$ . We see that Model B exhibits a long tail past the doubling time, which is consistent with a power-law scaling of the cycle duration probability. We find a criticality indicative scaling exponent of –3.05 for the CCDF after fitting the tail of the distributions of 5 independent realizations of the dynamics of Model B. (G) Box plots of the cycle length distributions as a function of control volume $V_{C}$ at birth. Cycle lengths are normalized by the doubling time $τ$ . Here, $V_{C}$ sets the molecular noise level to be equivalent to that of an exponentially growing cell born at $V_{C}$ but whose volume is reset to $V_{C}$ at each division. Note the very long tail of the distributions at small $V_{C}$ . (H) Position of the G1 attractor for inhibitor $[I]$ as a function of activator $[A]$ . The black dashed line corresponds to the level of $[A]$ which triggers a transition between two modes of growth and division as shown by the position of the G1 attractor for $[I]$ becoming equal to the concentration required to induce the G1/S transition. The two modes of growth are labeled [i] and [ii] and are also indicated in panels I-K. (I) Activator protein $[A]$ is synthesized in bursts whose amplitude and duration are a function of volume. We define the burst duration as the total time during which $[A]$ >0 for a cycle. The burst amplitude corresponds to the average level of $[A]$ during each G1 phase. Each burst is then color-coded as a function of the birth volume of the cell that induced it. We use a divergent colormap whose center value (light yellow) corresponds to the average volume of the cells at birth and is indicated by a notch on the colorbar. Here, [i] corresponds to the deterministic regime when volume is high and [ii] corresponds to the noisy regime when volume is low. Note that the average volume of the cells at birth is positioned close to the black dashed line. (J) Phase-space representation of the relaxation oscillator in the deterministic regime [i]. The X-coordinate shows the S/G2/M Switch variable, and the Y-coordinate shows the concentration of $[I]$ . Here, when volume is high, the position of the G1 attractor is *below* the $[I]$ concentration at which the G1/S transition happens. Thus, G1/S takes place and cells are in the cell cycle with a period of ~0.85. (K) Phase-space representation of the noisy regime [ii]. Here, when volume is low, the position of the G1 attractor becomes *greater* than the $[I]$ concentration at which the G1/S transition happens, and cells remain temporarily stuck in a prolonged G1 state and are unable to trigger the G1/S transition.

Appendix 1—figure 1

Download asset Open asset

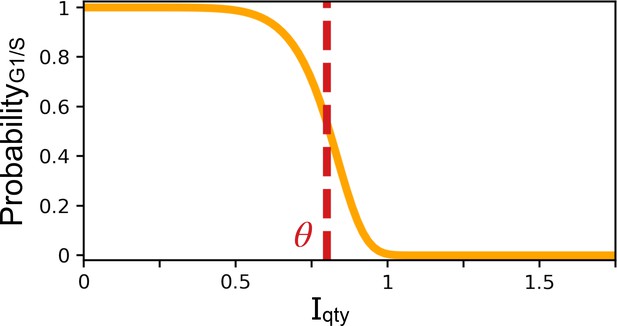
Probability of the G1/S transition occurring at the next time step.

X-coordinate is the quantity of the transcriptional regulator $I$ . Y-coordinate is the probability of the G1/S transition occurring at the next time step $Δ t$ . Parameters $θ = 0.8$ and $n_{θ} = 8$ .

Appendix 1—figure 2

Download asset Open asset

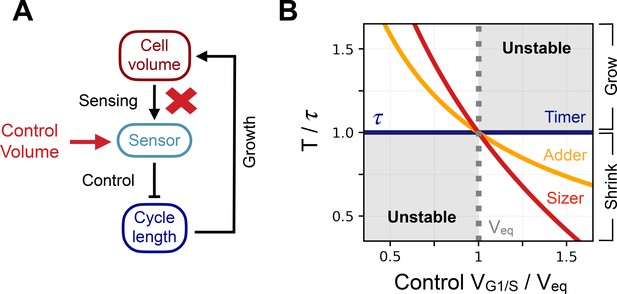
Control volume and archetype response curves.

(A) Schematic representation of the way we break the feedback in the system and impose a control volume $V_{C}$ (red arrow) at the G1/S transition in order to record the induced cell cycle period $T (V_{C})$ . (B) Response curve of the 3 size control archetypes. X-coordinate is the control volume at G1/S $V_{C}$ normalized by the equilibrium volume $V_{eq}$ . Y-coordinate is the response curve of the models $T (V_{C})$ normalized by the doubling time $τ$ . The dark blue curve is the response curve for the timer of length $τ$ , the orange curve the response curve for the adder, and the red curve the response curve for the sizer. The dotted grey line indicates the equilibrium volume $V_{eq}$ . The shaded region corresponds to the region where growth is unstable and volume diverges over successive generations.

Appendix 1—figure 3

Download asset Open asset

Response curves for the initial seed networks.

Columns indicate the size scaling assumption of the protein production rates as indicated above the figure. Rows indicate quantity or concentration sensing of inhibitor $I$ at the G1/S transition assumption as indicated on the left side of the figure. In each panel, we first show the seed network’s response curve $T (V_{C})$ as a function of control volume $V_{C}$ at G1/S. Sizer (red), adder (orange) and timer (dark blue) archetypes are shown for comparison. Second, we provide a schematic representation of the $[I]$ trajectory in G1. Schematic trajectories are shown for low volumes (light pink) and high volumes (dark red). (A) Quantity sensing of $I$ at G1/S with a size-dependent production rate in S/G2/M. Here, cells are born with a constant concentration $[I]$ . Because of the quantity sensing at G1/S, the concentration of $[I]$ at G1/S scales as $1 / V$ . Thus, the time spent in G1 scales with $V$ . This is the initial seed network we chose for most of our evolution experiments. (B) Quantity sensing of $I$ at G1/S with a size-independent production rate in S/G2/M. Here, cells are born with a concentration $[I]$ at birth that scales as $1 / V$ . Because of the quantity sensing at G1/S, we again find that the concentration of $[I]$ at G1/S scales as $1 / V$ . Thus, the time spent in G1 is constant. (C) Concentration sensing of $[I]$ at G1/S with a size-dependent production rate in S/G2/M. Here, cells are born with a constant concentration $[I]$ . Because of the concentration sensing at G1/S, we find that the concentration of $[I]$ at G1/S is constant. Thus, the time spent in G1 is constant. (D) Concentration sensing of $[I]$ at G1/S with a size-independent production rate in S/G2/M. Here, cells are born with a concentration $[I]$ that scales as $1 / V$ . Because of the concentration sensing at G1/S, we find that the concentration of $[I]$ at G1/S is constant. Thus, the time spent in G1 scales as $1 / V$ .

Appendix 1—figure 4

Download asset Open asset

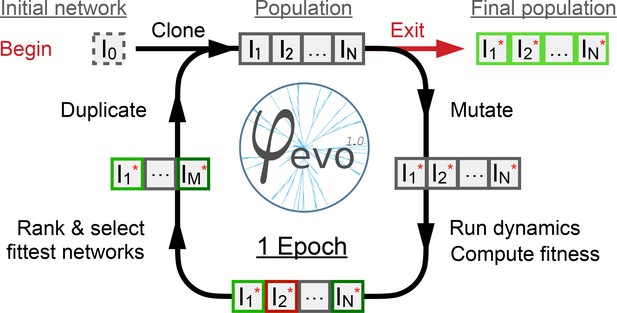
Schematic representation of the $φ$ -evo algorithm.

We begin with a user-defined initial seed network as starting point of the evolutionary process. The seed network is cloned to give a first population of networks. Individuals are then mutated randomly given the mutation parameters of the run. The dynamics and fitness scores of the networks are then computed and ranked. The best half of the population is selected and retained and the rest are discarded. The best half is then duplicated to maintain a constant population size $N$ . We then repeat these instructions for a predefined number of epochs, after which a final population of networks is extracted and analyzed.

Appendix 1—figure 5

Download asset Open asset

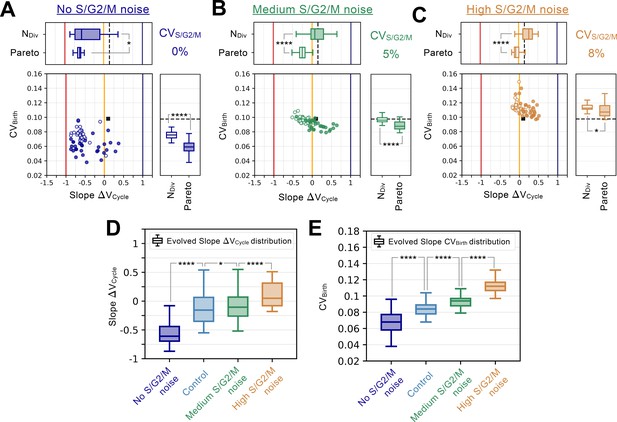
S/G2/M noise analysis.

Summary statistics for evolutionary simulations each having 500 epochs. Model A1 was used as the initial seed network. 30 simulations were performed using Pareto optimization of the number of divisions ( $N_{Div}$ ) and the CV of cell size at birth ( $C V_{Birth}$ ), are labeled Pareto and are shown in full colors. 30 more simulations were performed using only the number of divisions as the fitness function, are labeled $N_{Div}$ and are shown in colored outlines only. Scatter plots show the coefficient of variation of the size distribution at birth ( $C V_{Birth}$ , Y-coordinate) as a function of the fitted added volume slope over the whole cycle as a function of volume at birth (Slope $Δ V_{Cycle}$ , X-coordinate) for the most fit models evolved during each of the 60 independent simulations. Horizontal box plots above the scatter plots in A-C display the distributions of the added volume slopes for the Pareto and $N_{Div}$ simulations. Timer (dark blue), adder (orange) and sizer (red) slopes are shown respectively at 1, 0, and –1 for comparison. Vertical box plots on the right of the scatter plots in A-C show the distributions of $C V_{Birth}$ for the Pareto and $N_{Div}$ simulations. Asterisks represent p-values for the Welch’s t-Test between the distributions. For reference, $N S$ indicates $p > 0.05$ , * indicates $p < 0.05$ , ** indicates $p < 10^{- 2}$ , *** indicates $p < 10^{- 3}$ and **** indicates $p < 10^{- 4}$ . The values of $C V_{Birth}$ and Slope $Δ V_{Cycle}$ for the initial seed Model A1 are shown as a black square in the scatter plot or as a dashed black line in the box plots. Each panel explores different S/G2/M noise levels. (A) Evolution results for no noise in S/G2/M duration. (B) Evolution results for a noise level in S/G2/M duration equal to 5%. (C) Evolution results for a noise level in S/G2/M duration equal to 8%. (D) Evolved Slope $Δ V_{Cycle}$ distributions as a function of noise level in S/G2/M. For reference, noise level for the Control experiment from Figure 4 corresponds to 3%. Box plots in D-E represent the distributions for both the Pareto and $N_{Div}$ evolution experiments. Here, increased S/G2/M noise leads to loss of the sizer signature. (E) Evolved $C V_{Birth}$ distributions as a function of noise level in S/G2/M. Here, increased S/G2/M noise leads to increased variability in the cell size distributions at birth.

Appendix 1—figure 6

Download asset Open asset

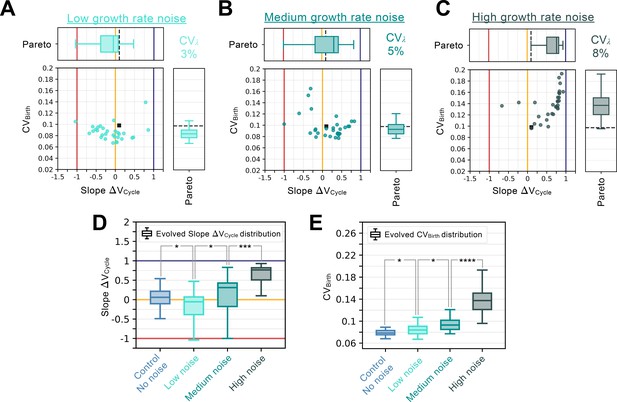
Growth rate noise analysis.

Summary statistics for evolutionary simulations each having 500 epochs. Model A1 was used as the initial seed network. Only 30 simulations were performed using Pareto optimization of the number of divisions ( $N_{Div}$ ) and the CV of cell size at birth ( $C V_{Birth}$ ), are labeled Pareto. Scatter plots show the coefficient of variation of the size distribution at birth ( $C V_{Birth}$ , Y-coordinate) as a function of the fitted added volume slope over the whole cycle as a function of volume at birth (Slope $Δ V_{Cycle}$ , X-coordinate) for the most fit models evolved during each of the 30 independent simulations. Horizontal box plots above the scatter plots in A-C display the distributions of the added volume slopes. Timer (dark blue), adder (orange) and sizer (red) slopes are shown respectively at 1, 0, and –1 for comparison. Vertical box plots on the right of the scatter plots in A-C show the distributions of $C V_{Birth}$ . Asterisks represent p-values for the Welch’s t-Test between the distributions. For reference, $N S$ indicates $p > 0.05$ , * indicates $p < 0.05$ , ** indicates $p < 10^{- 2}$ , *** indicates $p < 10^{- 3}$ and **** indicates $p < 10^{- 4}$ . The values of $C V_{Birth}$ and Slope $Δ V_{Cycle}$ for the initial seed Model A1 are shown as a black square in the scatter plot or as a dashed black line in the box plots. Each panel explores different growth rate noise levels. (A) Evolution results for low noise in growth rate with associated coefficient of variation at 3%. (B) Evolution results for medium noise in growth rate with associated coefficient of variation at 5%. (C) Evolution results for high noise in growth rate with associated coefficient of variation at 8% (D) Evolved Slope $Δ V_{Cycle}$ distributions as a function of noise level in the growth rate. For reference, noise level for the Control experiment from Figure 4 corresponds to no noise. Here, increased growth rate noise leads to rapid loss of the sizer signature. (E) Evolved $C V_{Birth}$ distributions as a function of noise level in the growth rate. Here, increased growth rate noise leads to increased variability in the cell size distributions at birth.

Appendix 1—figure 7

Download asset Open asset

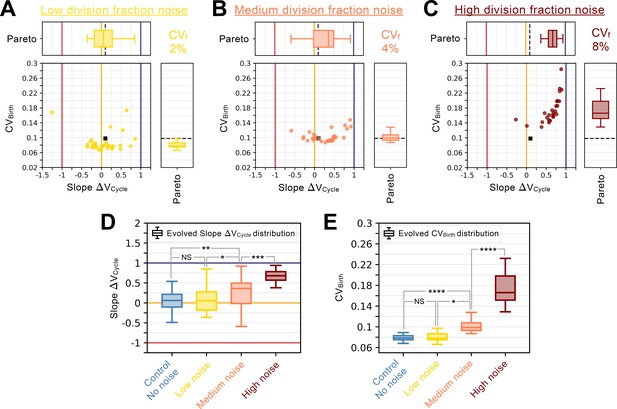
Division fraction noise analysis.

Summary statistics for evolutionary simulations each having 500 epochs. Model A1 was used as the initial seed network. Only 30 simulations were performed using Pareto optimization of the number of divisions ( $N_{Div}$ ) and the CV of cell size at birth ( $C V_{Birth}$ ), are labeled Pareto. Scatter plots show the coefficient of variation of the size distribution at birth ( $C V_{Birth}$ , Y-coordinate) as a function of the fitted added volume slope over the whole cycle as a function of volume at birth (Slope $Δ V_{Cycle}$ , X-coordinate) for the most fit models evolved during each of the 30 independent simulations. Horizontal box plots above the scatter plots in A-C display the distributions of the added volume slopes. Timer (dark blue), adder (orange) and sizer (red) slopes are shown respectively at 1, 0, and –1 for comparison. Vertical box plots on the right of the scatter plots in A-C show the distributions of $C V_{Birth}$ . Asterisks represent p-values for the Welch’s t-Test between the distributions. For reference, $N S$ indicates $p > 0.05$ , * indicates $p < 0.05$ , ** indicates $p < 10^{- 2}$ , *** indicates $p < 10^{- 3}$ and **** indicates $p < 10^{- 4}$ . The values of $C V_{Birth}$ and Slope $Δ V_{Cycle}$ for the initial seed Model A1 are shown as a black square in the scatter plot or as a dashed black line in the box plots. Each panel explores different division fraction $f$ noise levels. (A) Evolution results for low noise in division fraction with associated coefficient of variation at 2%. (B) Evolution results for medium noise in division fraction with associated coefficient of variation at 4%. (C) Evolution results for high noise in division fraction with associated coefficient of variation at 8%. 27/30 evolution runs succeeded and are shown here. (D) Evolved Slope $Δ V_{Cycle}$ distributions as a function of noise level in the division fraction. For reference, noise level for the Control experiment from Figure 4 corresponds to no noise. Here, increased noise leads to rapid loss of the sizer signature. (E) Evolved $C V_{Birth}$ distributions as a function of noise level in the division fraction. Here, increased noise leads to increased variability in the cell size distributions at birth.

Appendix 1—figure 8

Download asset Open asset

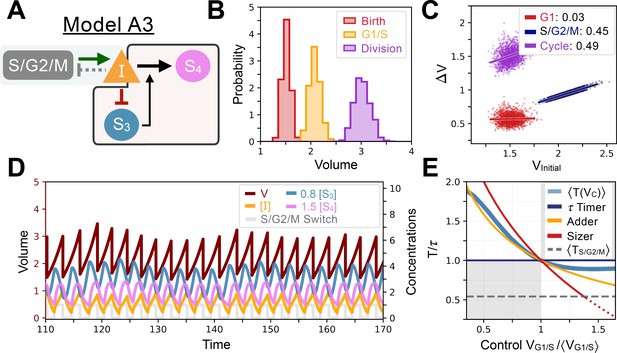
Model A3’s behavior.

(A) Network topology of the evolved Model A3. S₃ is as a size sensor and titrates $I$ in a size-dependent manner. (B) Size distributions at birth (red), G1/S (orange), and division (purple). (C) Added volumes in G1 (red), S/G2/M (blue) and over the whole cycle (purple) as a function of the volume at the beginning of those phases. (D) Temporal dynamics of the model, colors correspond to the variables in A. (E) Response curve $T (V_{C})$ as a function of control volume $V_{C}$ at the G1/S transition.

Appendix 1—figure 9

Download asset Open asset

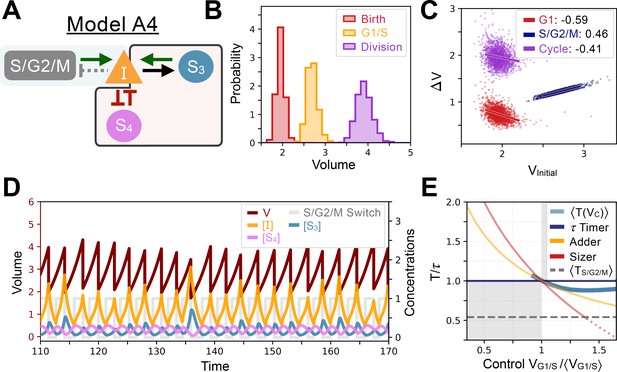
Model A4’s behavior.

(A) Network topology of the evolved Model A4. S₄ is the size sensor and represses the production of $I$ in a size-dependent manner. (B) Size distributions at birth (red), G1/S (orange) and division (purple). (C) Added volumes in G1 (red), S/G2/M (blue) and over the whole cycle (purple) as a function of initial volume at the start of those phases. (D) Temporal dynamics of the model, colors correspond to the variables in A. (E) Response curve $T (V_{C})$ as a function of control volume $V_{C}$ at the G1/S transition.

Appendix 1—figure 10

Download asset Open asset

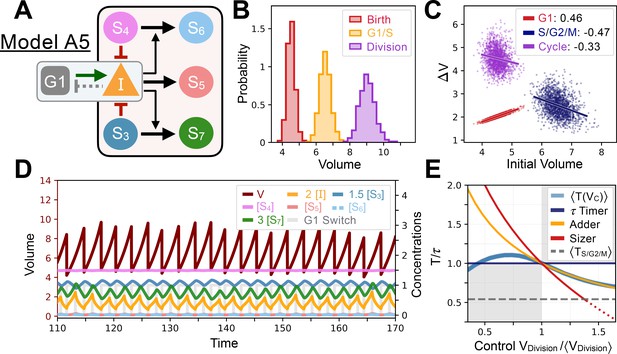
Model A5’s behavior.

(A) Network topology of the evolved Model A5. S₃ is the size sensor and represses the production of $I$ in a size-dependent manner. (B) Size distributions at birth (red), G1/S (orange) and division (purple). (C) Added volumes in G1 (red), S/G2/M (blue) and over the whole cycle (purple) as a function of initial volume at the start of those phases. (D) Temporal dynamics of the model, colors correspond to the variables in A. (E) Response curve $T (V_{C})$ as a function of control volume $V_{C}$ at division.

Appendix 1—figure 11

Download asset Open asset

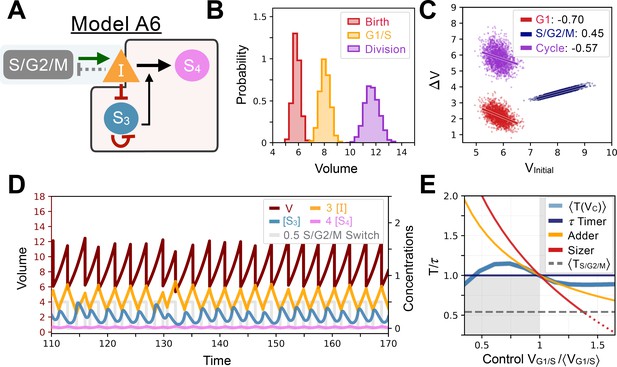
Model A6’s behavior.

(A) Network topology of the evolved Model A6. S₃ is the size sensor and represses the production of $I$ in a size-dependent manner. (B) Size distributions at birth (red), G1/S (orange) and division (purple). (C) Added volumes in G1 (red), S/G2/M (blue) and over the whole cycle (purple) as a function of initial volume at the start of those phases. (D) Temporal dynamics of the model, colors correspond to the variables in A. (E) Response curve $T (V_{C})$ as a function of control volume $V_{C}$ at the G1/S transition.

Tables

Appendix 1—table 1

Coefficients of variation: models and experiments.

Models		Data
Name	$C V_{Birth}$	Cell type	Time of size measure	$C V$
A1	0.098	Haploid budding yeast	Budding	0.17
A2	0.095	Haploid fission yeast	Fission	0.06
B	0.235	Mouse epidermal stem cell	Birth	0.17

Appendix 1—table 2

Model A1 parameter values.

Parameter	Value	Parameter	Value
p₂	0.369408	$δ_{3}$	0.4574764
$t_{1 : 2}$	1.104619	$k_{f 1}$	6.783001
$n_{1 : 2}$	3.215727	$k_{b 1}$	0.195168
$δ_{2}$	0.083827	$δ_{4}$	4.244007
p₃	0.703658	$k_{f 2}$	0.021174
$t_{2 : 3}$	0.044938	$k_{b 2}$	1.075146
$n_{2 : 3}$	3.266732	$δ_{5}$	1.1010876

Appendix 1—table 3

Model A2 parameter values.

Parameter	Value	Parameter	Value
$p_{2}$	1.915601	$n_{1 : 3}$	2.751652
$t_{1 : 2}$	0.17872	$t_{2 : 3}$	0.441106
$n_{1 : 2}$	2.09054	$n_{2 : 3}$	2.780297
$t_{3 : 2}$	0.962612	$δ_{3}$	0.045051
$t_{3 : 2}$	2.144666	$k_{f 1}$	0.839879
$δ_{2}$	0.019495	$k_{b 1}$	0.381067
$p_{3}$	1.944803	$δ_{4}$	0.913992
$t_{1 : 3}$	0.422939	0

Appendix 1—table 4

Model B parameter values.

Parameter	Value	Parameter	Value
p₂	4.968896	$n_{3 : 3}$	3.189190
$t_{1 : 2}$	2.569361	$δ_{3}$	0.246561
$n_{1 : 2}$	0.952178	p₄	4.674459
$t_{3 : 2}$	0.131057	$δ_{4}$	1.010978
$n_{3 : 2}$	9.219961	k_f	3.194116
$δ_{2}$	0.521437	k_b	4.634009
p₃	0.113586	$δ_{5}$	1.165439
$t_{3 : 3}$	2.183079	C₀	1

Appendix 1—table 5

Model A3 parameter values.

Parameter	Value	Parameter	Value
p₂	5.606156	$t_{2 : 3}$	1.410420
$t_{1 : 2}$	0.066136	$n_{2 : 3}$	3.434213
$n_{1 : 2}$	8.177965	k_f	1.930909
b₂	0.911279	k_b	3.871610
$δ_{2}$	0.257920	$δ_{3}$	0.013294
p₃	5.887584	$δ_{4}$	1.803926

Appendix 1—table 6

Model A4 parameter values.

Parameter	Value	Parameter	Value
p₂	5.6604334	$δ_{2}$	0.001059
$t_{1 : 2}$	0.408208	k_f	0.843408
$n_{1 : 2}$	1.769233	k_b	1.680321
$t_{3 : 2}$	0.887392	$δ_{3}$	0.825150
$n_{3 : 2}$	6.437683	p₄	4.674459
$t_{4 : 2}$	0.197495	$t_{2 : 4}$	0.744119
$n_{4 : 2}$	3.238633	$n_{2 : 4}$	3.451469
b₂	0.800255	$δ_{4}$	1.929584

Appendix 1—table 7

Model A5 parameter values.

Parameter	Value	Parameter	Value
p₂	2.379635	b₄	2.624939
$t_{1 : 2}$	0.142770	$δ_{4}$	1.499653
$n_{1 : 2}$	0.383384	$δ_{5}$	0.006318
$t_{3 : 2}$	0.714386	$δ_{6}$	0.983140
$n_{3 : 2}$	8.642875	$δ_{7}$	0.481592
$t_{4 : 2}$	1.754776	$k_{f 1}$	0.226150
$n_{4 : 2}$	7.783080	$k_{b 1}$	3.793388
b₂	0.195855	$k_{f 2}$	1.608325
$δ_{2}$	0.576282	$k_{b 2}$	3.322565
b₃	0.582449	$k_{f 3}$	2.999118
$δ_{3}$	0.318466	$k_{b 3}$	0.906997

Appendix 1—table 8

Model A6 parameter values.

Parameter	Value	Parameter	Value
p₂	0.369408	$δ_{2}$	0.093159
$t_{1 : 2}$	0.748731	$k_{f 1}$	0.533415
$n_{1 : 2}$	3.850889	$k_{b 1}$	3.141514
p₃	3.868044	$δ_{3}$	0.626507
$t_{2 : 3}$	0.082081	$k_{f 2}$	3.911233
$n_{2 : 3}$	3.638939	$k_{b 2}$	1.885120
$t_{3 : 3}$	0.599375	$δ_{4}$	0.821609
$n_{3 : 3}$	6.300643	$δ_{5}$	1.882484