A unified approach to dissecting biphasic responses in cell signaling
- Department of Chemical Engineering, Sargent Centre for Process Systems Engineering, Imperial College London, United Kingdom
- Institute for Systems and Synthetic Biology, Imperial College London, South Kensington Campus, United Kingdom
Figures
Figure 1 with 1 supplement
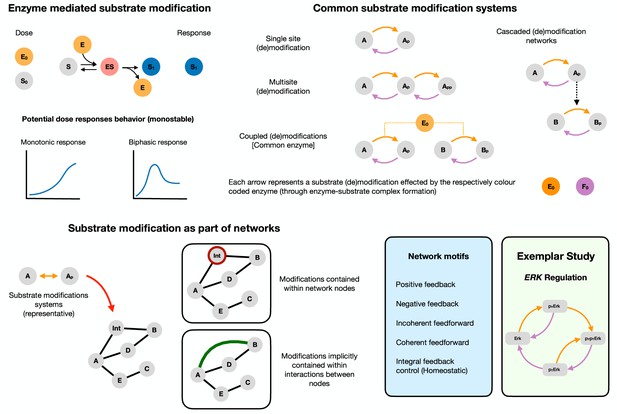
Biphasic dose responses in basic building blocks in cell signaling: from enzyme-mediated substrate modification systems to network motifs/modules Reversible enzyme-mediated substrate modification is an integral part of cellular signaling and is among its basic building blocks.
Top left shows the basic mechanism of substrate modification by an enzyme involving the following steps: the binding (and unbinding) of the substrate () with the enzyme () to form a substrate-enzyme complex (), which finally disassociates to give the modified substrate () and the free enzyme (). The reverse modification is not depicted for conciseness. The output of the system is the concentration of the modified substrate . There are two natural doses associated with this - total substrate amount and total enzyme amount ( and , respectively). The potential dose-response behavior in the simplest instance can thus be either (a) monotonic or (b) exhibit biphasic dependence of the modified substrate with the dose. Both substrate and enzyme doses can potentially elicit biphasic responses. Top right shows the schematics of commonly encountered substrate modification building block systems in cell signaling. Each arrow denotes a modification and involves binding, unbinding and catalytic action by the enzyme. Arrows of the same color indicate action by the same enzyme type (a kinase and a phosphatase for example). Bottom left These systems form key components of wider signaling networks in the cell. From a network perspective they can be incorporated in two ways. (1) They can either be explicitly described, for example as part of a node or (2) be implicitly present within an interaction between nodes (implicit in an arrow, which can be the sum of actions of species not explicitly defined). A fruitful way to study signaling networks is through the study of recurring signaling motifs (with characteristic input-output responses) such as feedback and feedforward structures. Bottom right lists canonical network motifs (positive and negative feedback, and coherent and incoherent feedforward, integral feedback control) that we study in our work. We complement our study of biphasic responses in biochemical building-block systems and network motifs by studying biphasic responses in a concrete exemplar system, the ErK signaling pathway. Detailed mathematical model descriptions of all the systems studied are discussed in the supplementary material, and a detailed reaction schematic of the models considered is shown in Figure 1—figure supplement 1.
Figure 1—figure supplement 1
Schematic representation of the various models considered in the manuscript.
Models M0-M1 represents the basic unit of (de)modification, the covalent modification cycle and its simple extension with the substrate forming an additional complex with the enzyme. Models M2-M5 represent different systems of ordered distributive double site modification of a substrate (by different or common enzymes acting on each modification site). Models M6-M7 represent other architectures of modification systems in chemical reaction networks, such as cascaded systems (with different and common enzymes affecting (de)modification) and coupled covalent modification networks (coupled through enzyme sharing in (de)modification). Models N0-N5, represent different networks and network motifs with biphasic dose-response subsumed in an interaction.
Figure 2 with 4 supplements
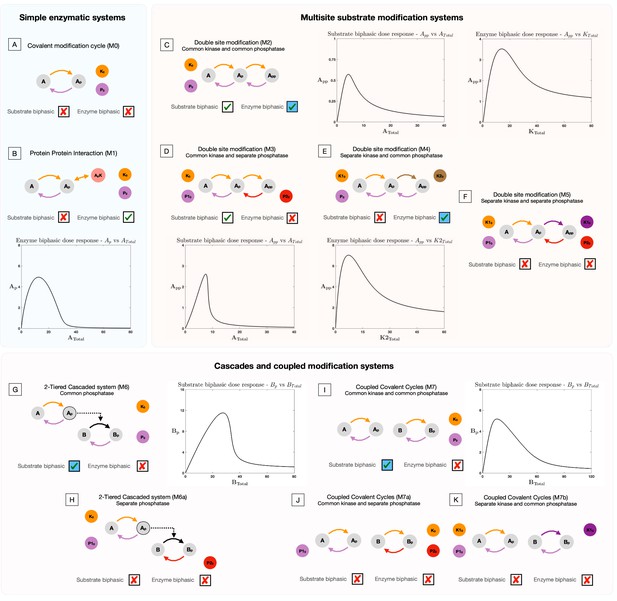
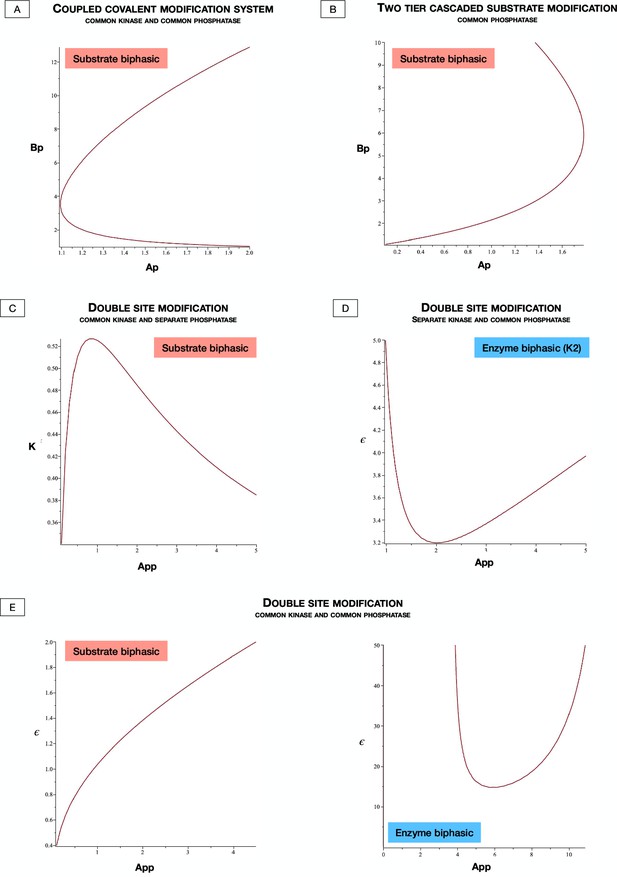
Presence and absence of substrate and enzyme biphasic dose responses in the commonly observed building blocks of cellular signaling systems.
An examination of a suite of substrate modification systems and different doses allows us to clearly ascertain the origin and necessary features of such systems to present enzyme and substrate biphasic dose responses. Where results denote a biphasic response is absent (indicated by a cross in a box), this is absent irrespective of kinetic parameter values and total amounts of substrate(s) and enzyme(s). This is established through analytical work (see Supplementary file 1). When a biphasic dose-response is present, it is shown in a bifurcation diagram where the relevant dose is the bifurcation parameter. The presence of specific dose-responses can be characterized in parameter space in the following way, either the behavior is (1) present for all intrinsic kinetic parameter values (accessible for some total amounts of substrate and enzyme, transparent boxes with a tick), or (2) present only for specific intrinsic kinetic parameter values (accessible for some total amounts of substrate and enzymes, blue-shaded boxes with a tick) - see text and analytical work for more details. (A) Covalent modification system. Absence of substrate and enzyme biphasic response. (B) Protein-Protein Interaction Model. Enzyme biphasic dose responses are seen in the protein-protein interaction model, but substrate biphasic responses are absent. In contrast to the covalent modification cycle which is incapable of biphasic responses, this result indicates how a single additional complex formation by the enzyme (and resulting sequestration) can generate enzyme biphasic dose responses. (C) Double site modification (DSP): common enzymes. Presence of enzyme and substrate biphasic response (enzyme biphasic responses only for certain ranges of intrinsic kinetic parameter values - see text). (D) DSP: common kinase and separate phosphatase. Presence and absence of substrate and enzyme biphasic response, respectively. (E) DSP: separate kinase and common phosphatase. Absence and presence of substrate and enzyme biphasic response, respectively (enzyme biphasic only with respect to the total amount of the second kinase, and only for certain ranges of intrinsic parameter values- see text). (F) DSP: separate kinase and separate phosphatase. Absence of both substrate and enzyme biphasic response. These results together show how commonality of both enzymes promotes biphasic responses with both doses, and in particular how commonality in phosphatase and kinase action enables enzyme and substrate biphasic responses, respectively. (G, H) Two-tier enzymatic cascades with common and separate phosphatases, respectively. Presence of substrate biphasic in the second-tier substrate of the two-tier cascaded enzymatic modification system with a common phosphatase. The first tier substrate is incapable of substrate biphasic in the same model. Both tier substrates are incapable of substrate biphasic responses when the phosphatases are distinct. Enzyme biphasic responses are absent in both systems. (I–K) Coupled covalent modification cycles with common and separate enzymes. Presence and absence respectively of substrate and enzyme biphasic responses in the system with common kinases and common phosphatases. The system with separate phosphatases and the system with separate kinases are incapable of substrate and enzyme biphasic responses. (G–K) indicates how commonality of enzymes can enable biphasic responses in covalent modification systems, which are either otherwise decoupled (I, J) or where they are part of a cascade (G, H). This highlights how such features emerge, even though the constituent modules (covalent modification cycles) are incapable of it.
Figure 2—figure supplement 1
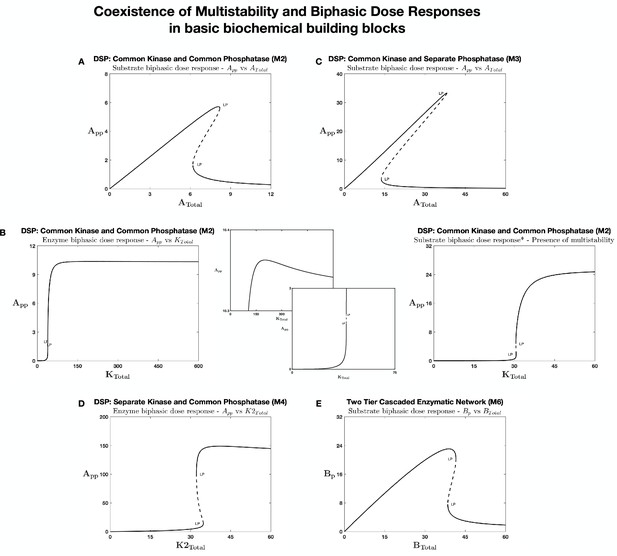
Coexistence of multi-stability and biphasic dose response in various enzymatic models for the same underlying kinetic regime.
The above panels illustrate computational evidence of the possibility of coexistence of biphasic response with multi-stability, in a 1D bifurcation along the respective dose (for the same/similar underlying kinetics), for the different networks considered. The results are shown for all models capable of biphasic response (from within our study) and multistability. Note that a coupled covalent system (with common kinase) while capable of substrate biphasic is incapable of multistabilty. (A) Double site modification (DSP) with common kinase and phosphatase: Substrate biphasic response and multistability for the same underlying kinetics. (B) DSP with common kinase and common phosphatase: Enzyme biphasic response and multistability - for different (but close) parameter regimes. Inset plots show magnified regions from the main figure. (C) DSP with common kinase and separate phosphatase. Substrate biphasic response and multistability for the same underlying kinetics. (D) DSP with separate kinase and common phosphatase. Enzyme biphasic response and multistability for the same underlying kinetics. (E) Two-tier cascaded enzymatic network. Substrate biphasic response and multistability for the same underlying kinetics. This shows how the enzymatic modification mechanism (and the associated sequestration and non-linearity in interaction) within these networks allows for not just the capacity to present biphasic dose response behavior but also to be present in conjunction with other qualitative signaling behaviors. [LP: saddle-node bifurcation, solid, and dotted lines denote stable and unstable steady states, respectively].
Figure 2—figure supplement 2
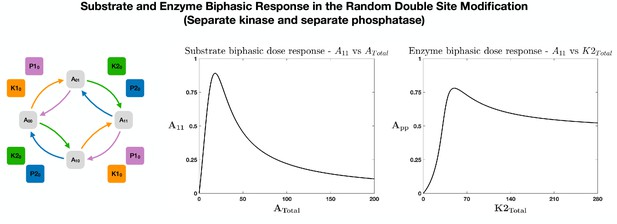
Biphasic responses in random double site modification network with separate enzymes effecting each modification.
While the ordered double site modification (DSP) with separate enzymes acting on each modification site is incapable of exhibiting any biphasic dose response, random ordered (de)modification exhibits both substrate (left) and enzyme (right) biphasic dose response. This illustrates how additional complexity (inherently) associated with enzyme-mediated substrate modification (random) can further expand the propensity for such networks containing them to generate biphasic dose response.
Figure 2—figure supplement 3
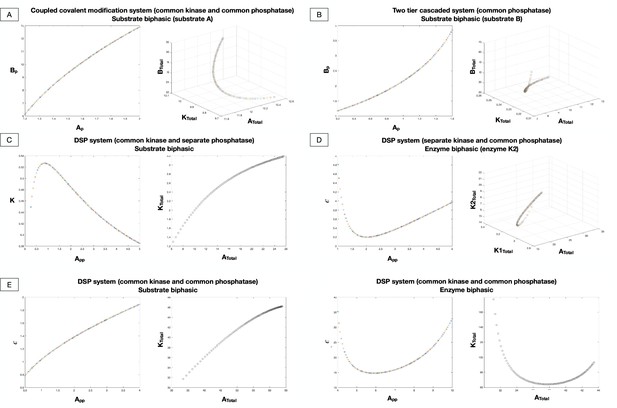
Exploration of the effect of species total amounts in allowing for biphasic responses in different modification systems.
There are two kinds of parameters in substrate modification systems: intrinsic rate constants and species total amounts. Analytical work has characterized the possibility or impossibility of obtaining biphasic responses and the dependence on intrinsic rate constants. Semi-analytical work (presented here and in Figure 2—figure supplement 4) provides further analysis into how species amounts can allow for biphasic responses. For each of the systems considered, we first fix intrinsic kinetic rate constants at or close to those seen experimentally in a reference system (see Witzel and Blüthgen, 2018). We then semi-analytically explore the steady state equations by systematically reducing them and requiring the presence of a biphasic response. In all cases, the presence of biphasic responses (or specifically the onset of biphasic responses, i.e. biphasic peak) is shown by a curve involving two concentration variables. Each point along this curve denotes a concentration variable pair, that will guarantee the onset of biphasic response at the given value. Using these concentrations, the total amounts of all relevant species can be back-calculated (for every point on this curve) easily to ascertain what total amounts are to be needed for the behavior (also see Figure 2—figure supplement 4). Sample calculations for a representative point on each curve is presented in the Supplementary file 2. It is shown by sampling a given point from each of these graphs, that the resulting total amounts of substrates and enzymes are also within the ranges of those accessible by experiments (see Supplementary file 2 for more detail). All concentrations shown are in µM (A) Coupled covalent modification cycles (B) Two-tier enzymatic cascade (C) Double site modification system with common kinase and separate phosphatase (D) Double site modification system with separate kinase and common phosphatase (E) Double site modification with common kinase and common phosphatase (note that ). The values of total amounts of one of the enzymes (and in where multiple enzymes (kinases/phosphatases) are involved, two of the enzymes), are fixed at levels in physiological ranges, and the total amounts of other species are explored. This is to allow for the creation and easy visualization of contour plots.
Figure 2—figure supplement 4
Semi-analytical approach for determining total amounts of species for realizing biphasic responses.
This figure provides complementary information to Figure 2—figure supplement 4 into how species total amounts can allow for biphasic responses. For each of the systems considered, as discussed in Figure 2—figure supplement 4 we first fix intrinsic kinetic rate constants at or close to those seen experimentally in a reference system. We then semi-analytically explore the steady state equations by systematically reducing them and requiring the presence of a biphasic response. In all cases, the presence of biphasic responses (or specifically the onset of biphasic responses i.e. biphasic peak) is shown by a curve involving two concentration variables in different ways. On one hand, we show the curve relating two concentration variables (as shown in Figure 2—figure supplement 4). On the other hand, the curve has also been translated into curves in total amounts and that is shown in a separate panel. This demonstrates that biphasic responses can be readily obtained for biologically reasonable total amounts (all total amounts and concentrations are in µM). (A) Coupled covalent modification cycles (B) Two-tier enzymatic cascade (C) Double site modification system with common kinase and separate phosphatase (D) Double site modification system with separate kinase and common phosphatase (E) Double site modification with common kinase and common phosphatase (). The values of total amounts of one of the enzymes (and in where multiple enzymes (kinases/phosphatases) are involved, two of the enzymes), are fixed at levels in physiological ranges, and the total amounts of other species are explored. This is to allow for the creation and easy visualization of contour plots.
Figure 3 with 2 supplements
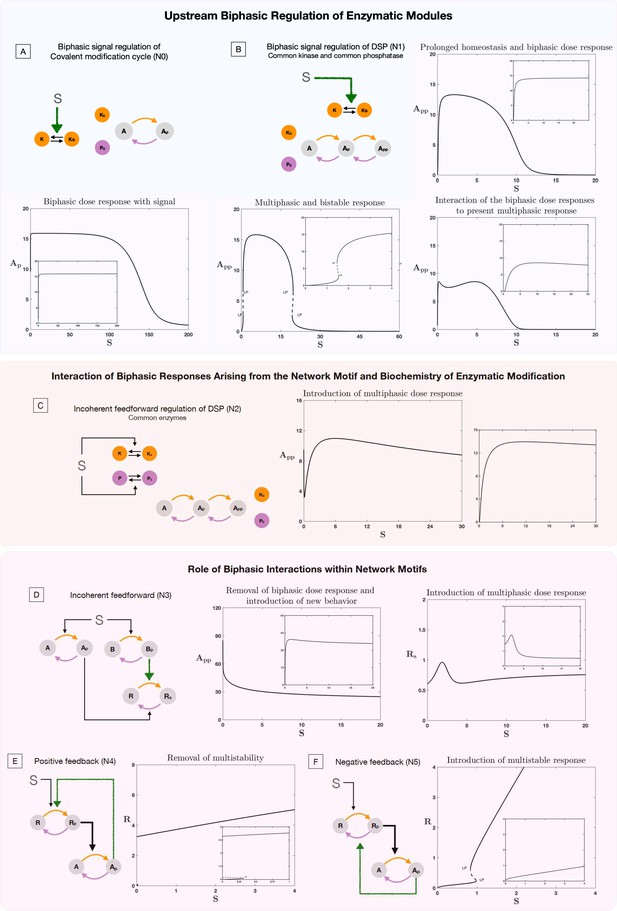
Role of biphasic interactions in network and motif response.
The results presented in this plot show the consequence of biphasic signal regulation and biphasic response within interactions in enabling network response. In each plot the inset image represents the basal behavior in the absence of biphasic signal regulation or biphasic interaction, for the same kinetic parameters of the system. (A–B). Role of biphasic signal regulation in perturbing behavior of enzymatic systems, (A) Covalent modification cycle and (B) double site modification (DSP) (common enzymes). (A) shows how biphasic signal regulation can enable homeostatic (prolonged flat region) and biphasic response from a covalent modification cycle (note that the response is an increasing function of dose for small signal values). (B) shows how biphasic signal regulation can enable not just biphasic behavior (top right panel) but multiphasic behavior (bottom right panel), and result in a dose response curve with multiple multistable regions (indicated by pairs of limit points) along with a biphasic response (bottom left panel). (C) contrasts this with the response from incoherent feedforward regulation of the DSP (a driver of biphasic responses), which can similarly present multiphasic responses (note that the curve decreases before increasing and decreasing again) (plot to the right shows behavior without incoherent feedforward regulation, where such behavior is absent). (D–F) Effect of biphasic interaction on common network regulatory motifs. Biphasic interaction can alter the fundamental feature of feedforward motifs in multiple ways. (D) In incoherent feedforward networks, it can destroy the expected biphasic response (left panel) and also enable the creation of multiphasic responses (right panel). Similarly, in feedback networks, it can destroy multi-stability in a positive feedback motif (E). On the other hand, it can erode homeostatic responses and enable multistability in negative feedback motifs (the later shown in F). [Colored straight arrows in network schematics represent biphasic interactions. LP: saddle-node bifurcation, solid lines, and dotted lines denote stable and unstable steady state, respectively].
Figure 3—figure supplement 1
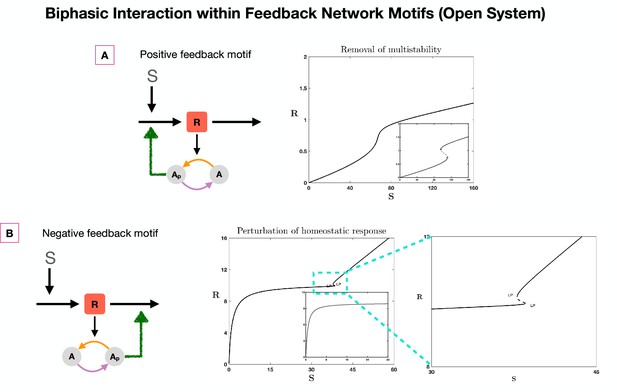
Effect of biphasic response in interactions within feedback network motifs (open systems): The figure shows the introduction of novel behavior (bistability in NFB, see (B)), and the removal of expected behavior (bistability in PFB, see (A)) even when the biphasic responses in interactions are present within open system feedback network motifs.
This complements our analysis in the paper where similar results were shown with motifs constructed with closed system (see Figure 3—figure supplement 1). The inset plots show basal behavior without the biphasic interaction. (B) shows expanded region in the aside main plot. [Brown arrows in the network schematics represent biphasic interactions. LP: saddle node bifurcation. Solid lines and dotted lines denote steady and unstable steady states, respectively.].
Figure 3—figure supplement 2
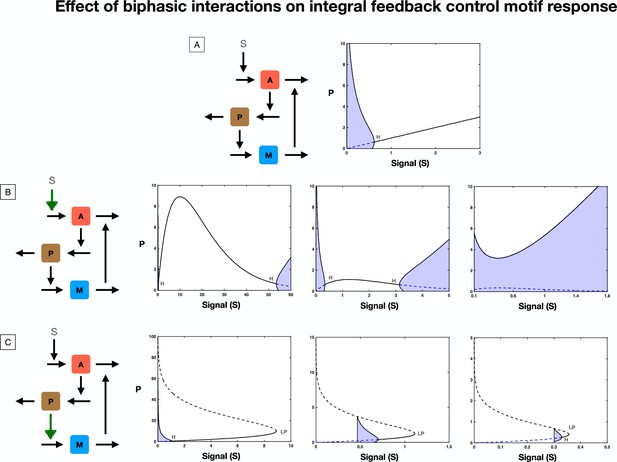
Effect of biphasic response in interactions within integral feedback control motif: perturbation of expected homeostatic response.
The simple integral feedback control motif is capable of exact homeostasis in the substrate form M, as signal (S) and substrate forms P and A change (see plot A, M not shown). The lower regions of signal activation are unstable for the system and oscillate. There exists a threshold of signal above which the single steady state is stable and there is steady exact homeostasis in M. In plots B and C, we show how the expected response from the motif can be affected by (1) biphasic signal regulation (B), (2) biphasic response in an interaction within the motif (C). (B) shows how upstream biphasic signal regulation can diminish the range over which stable steady state homeostatic response is seen (in the concentration of M - not shown), by making the system unstable through a hopf bifurcation leading to oscillations, for both low signal and high signal ranges. Depending on the nature and strength of the biphasic signal regulation (manipulated here by changing parameter values associated with the signal regulation), the stable steady state regime in signal can diminish and for a sufficiently strong biphasic signal regulation, the system can be completely unstable, completely undermining the exact homeostasis expected in M from the motif. (C) shows how biphasic responses in an interaction within the motif (indicated in the adjacent schematic with a brown arrow) can further arrest the expected biphasic response by ‘capping’ the signal range over which the motif can function (due to the saturating effect from the biphasic response - see text). Furthermore, the steady state of the system can lose stability even for lower signal ranges (on the existing stable branch), due to oscillations. Thus, biphasic interactions within even a robust homeostatic motif such as integral feedback control can fundamentally subvert expected motif response [Brown arrows in the network schematics represent biphasic interactions. LP: saddle node bifurcation. H: Hopf point bifurcation. Solid lines and dotted lines denote steady and unstable steady states, respectively. Regions shaded in blue represent oscillations.].
Figure 4
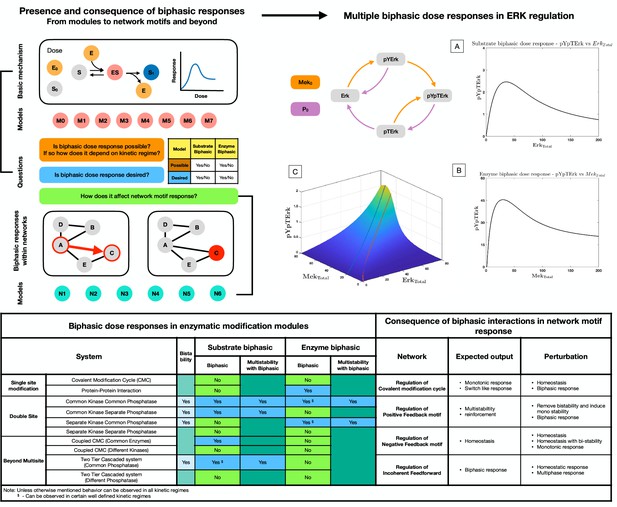
Presence and consequence of biphasic dose responses in cellular signaling arising from enzyme-mediated substrate modification: Top left hand panel: Schematic representation of the study.
The basic mechanism of enzyme-mediated substrate modification (when present in different reversible modification cycles) allows for simple biochemical systems to present biphasic dose-response behavior. This is analyzed in a series of commonly encountered biochemical building blocks of cell signaling (M0-M8, see Figure 1—figure supplement 1 for detailed schematic). In each case, we assess whether the system exhibits biphasic behavior with respect to variation of total amounts of enzyme and substrate as doses, and if it does so robustly. The table below provides a classification system to determine the different possibilities of biphasic responses (enzyme/substrate) vis-a-vis the desirability/undesirability of biphasic responses. This provides a framework (in synthetic biology) for determining what changes need to be made to a system, to obtain desirable characteristics. We then extend the study to consider the consequence of such biphasic dose responses in network motif structures (either within nodes, or in interactions–colored in red) and study how biphasic interactions can alter expected outcomes from these systems (N1–N5). Top right hand panel: Case study: Extracellular signal-regulated kinase (Erk) Regulation. The ERK regulatory network is capable of both exhibiting substrate and enzyme biphasic response in the double phosphorylated Erk (pYpTErk) in the steady state dose response with (Enzyme biphasic) and (Substrate biphasic). A-B shows an instance of enzyme and substrate biphasic response, respectively. (C) shows how the steady state concentration of pYpTErk changes with and (for a fixed kinetic parameter set). This indicates the presence of simultaneous substrate and enzyme biphasic response in the system (red and blue lines indicate the peak concentration of pYpTErk achieved for a given amount of total substrate and total enzyme amounts, respectively). Bottom panel. Table: Detailed summary of the various results discussed in the manuscript, including the possibility and impossibility of specific dose-response behaviors in a model, and the different ways in which the expected outcome of a network motif structure is undercut by biphasic responses within interactions. Note: These results discuss analytical results which can be found in Supplementary file 1.
Additional files
-
MDAR checklist
- https://cdn.elifesciences.org/articles/86520/elife-86520-mdarchecklist1-v2.docx
-
Supplementary file 1
PDF Version of Source code 1.
- https://cdn.elifesciences.org/articles/86520/elife-86520-supp1-v2.pdf
-
Supplementary file 2
PDF Version of Source code 2.
- https://cdn.elifesciences.org/articles/86520/elife-86520-supp2-v2.pdf
-
Source code 1
Analysis of models.
- https://cdn.elifesciences.org/articles/86520/elife-86520-code1-v2.zip
-
Source code 2
Further analysis of models.
- https://cdn.elifesciences.org/articles/86520/elife-86520-code2-v2.zip
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
A unified approach to dissecting biphasic responses in cell signaling
eLife 12:e86520.
https://doi.org/10.7554/eLife.86520
