Research Article

Neuroscience

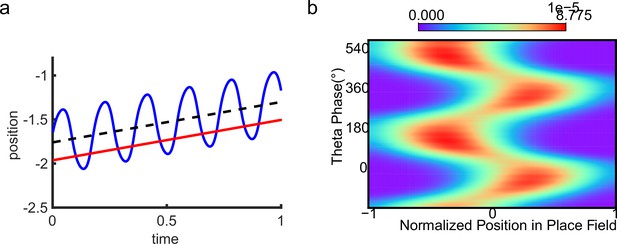
Firing rate adaptation affords place cell theta sweeps, phase precession, and procession

School of Psychological and Cognitive Sciences, IDG/McGovern Institute for Brain Research, Center of Quantitative Biology, Peking-Tsinghua Center for Life Sciences, Academy for Advanced Interdisciplinary Studies, Peking University, China
Institute of Cognitive Neuroscience, University College London, United Kingdom
Department of Psychology, Tsinghua University, China
Lyda Hill Department of Bioinformatics, O’Donnell Brain Institute, The University of Texas Southwestern Medical Center, United States
School of Computer Science, Peking University, China
Department of Neuroscience, Physiology and Pharmacology, University College London, United Kingdom

Jul 22, 2024

https://doi.org/10.7554/eLife.87055.4

Open access
Copyright information

Figures
Videos
Tables
Additional files

16 figures, 4 videos, 3 tables and 2 additional files

Figures

Figure 1

Download asset Open asset

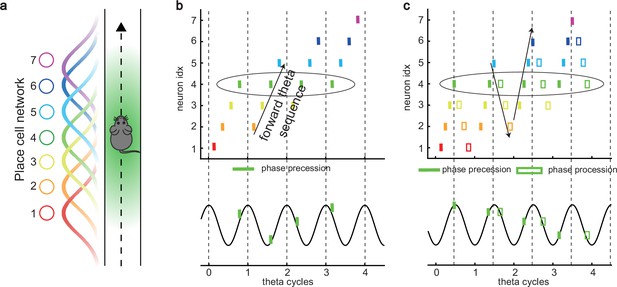
Theta sequence and theta phase shift of place cell firing.

(a) An illustration of an animal running on a linear track. A group of place cells each represented by a different color are aligned according to their firing fields on the linear track. (b) An illustration of the forward theta sequences of the neuron population (upper panel), and the theta phase precession of the fourth place cell (represented by the green color, lower panel). (c) An illustration of both forward and reverse theta sequences (upper panel), and the corresponding theta phase precession and procession of the fourth place cell (lower panel). The sinusoidal trace illustrates the theta rhythm of local field potential (LFP), with individual theta cycles separated by vertical dashed lines.

Figure 2

Download asset Open asset

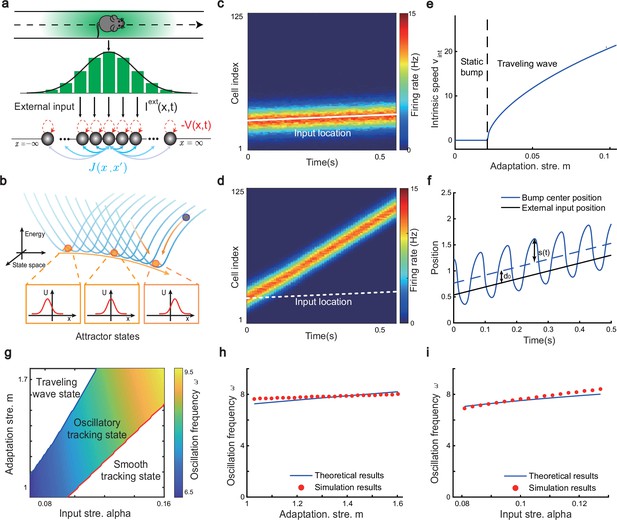
The network architecture and tracking dynamics.

(a) A one-dimensional (1D) continuous attractor neural network (CANN) formed by place cells. Neurons are aligned according to the locations of their firing fields on the linear track. The recurrent connection strength $J (x, x^{'})$ (blue arrows) between two neurons decays with their distance on the linear track. Each neuron receives an adaptation current $- V (x, t)$ (red dashed arrows). The external input $I^{e x t} (x, t)$ , represented by a Gaussian-shaped bump, conveys location-dependent sensory inputs to the network. (b) An illustration of the state space of the CANN. The CANN holds a family of bump attractors which form a continuous valley in the energy space. (c) The smooth tracking state. The network bump (hot colors) smoothly tracks the external moving input (the white line). The red (blue) color represents high (low) firing rate. (d) The traveling wave state when the CANN has strong firing rate adaptation. The network bump moves spontaneously with a speed much faster than the external moving input. (e) The intrinsic speed of the traveling wave versus the adaptation strength. (f) The oscillatory tracking state. The bump position sweeps around the external input (black line) with an offset $d_{0}$ . (g) The phase diagram of the tracking dynamics with respect to the adaptation strength $m$ and the external input strength $α$ . The colored area shows the parameter regime for the oscillatory tracking state. Yellow (blue) color represents fast (slow) oscillation frequency. (**h and i**) Simulated (red points) and theoretical (blue line) oscillation frequency as a function of the adaptation strength (h) or the external input strength (i).

Figure 3

Download asset Open asset

Oscillatory tracking accounts for theta sweeps and theta phase shift.

(a) Snapshots of the bump oscillation along the linear track in one theta cycle (0–140 ms). Red triangles indicate the location of the external moving input. (b) Decoded relative positions based on place cell population activities. The relative locations of the bump center (shown by the neural firing rates of 10 most active neurons at each timestamp) with respect to the location of the external input (horizontal line) in five theta cycles. See a comparison with experimental data in Wang et al., 2020, Figure 1a lower panel. (c) Upper panel: The process of the animal running through the firing field of the probe neuron (large black dot) is divided into three stages: the entry stage (green), the phase shift stage (red), and the departure stage (blue). Lower panel: The displacement between the bump center and the probe neuron as the animal runs through the firing field. The horizontal line represents the location of the probe neuron, which is $x = 0$ . (d) The firing rates of the probe neuron as the animal runs through the firing field. Colored points indicate firing peaks. The trace of the firing rate in the phase shift stage (the dashed box) is enlarged in the sub-figure on the right-hand side, which exhibits both phase precession (red points) and procession (blue points) in successive theta cycles. (e) The firing phase shift of the probe neuron in successive theta cycles. Red points progress to earlier phases from $π / 2$ to $- π / 2$ and blues points progress to later phases from $π / 2$ to $3 π / 2$ . The color of the dots represent the peak firing rates, which is also shown in (d).

Figure 4

Download asset Open asset

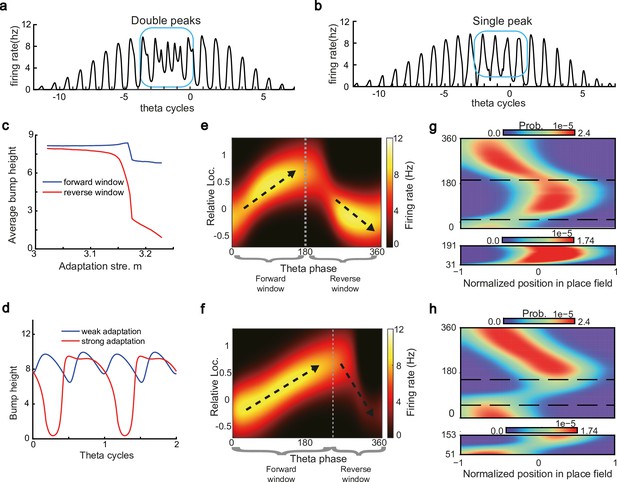
Different adaptation strengths account for the emergence of bimodal and unimodal cells.

(a) The firing rate trace of a typical bimodal cell in our model. Blue boxes mark the phase shift stage. Note that there are two peaks in each theta cycle. (b) The firing rate trace of a typical unimodal cell. Note that there is only one firing peak in each theta cycle. For a comparison to (a) and (b), see experiment data shown in Skaggs et al., 1996, Figure 6. (c) The averaged bump heights in the forward (blue curve) and backward windows (red curve) as a function of the adaptation strength $m$ . (d) Variation of the bump height when the adaptation strength is relatively small (blue line) or large (red line). (**e and f**) Relative location of the bump center in a theta cycle when adaptation strength is relatively small (e) or large (f). Dashed line separate the forward and backward windows. (**g and h**) Theta phase as a function of the normalized position of the animal in place field, averaged over all bimodal cells (g) or over all unimodal cells (h). –1 indicates that the animal just enters the place field, and 1 represents that the animal is about to leave the place field. Dashed lines separate the forward and backward windows. The lower panels in both (g and h) present the rescaled colormaps only in the backward window.

Figure 5

Download asset Open asset

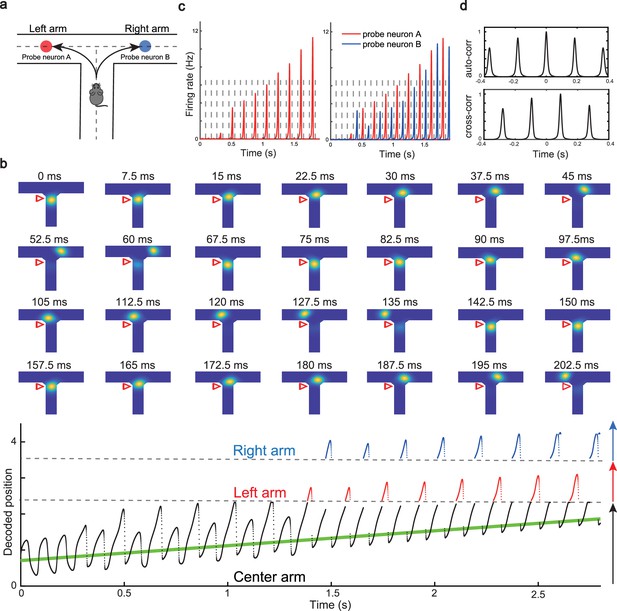
Constant cycling of future positions in a T-maze environment.

(a) An illustration of an animal navigating a T-maze environment with two possible upcoming choices (the left and right arms). (b) Upper panel: Snapshots of constant cycling of theta sweeps on two arms when the animal is approaching the choice point. Red triangle marks the location of the external input. Note that the red triangle moves slightly toward the choice point in the 200 ms duration. Lower panel: Constant cycling of two possible future locations. The black, red, and blue traces represent the bump location on the center, left, and right arms, respectively. The green line marks the location of the external moving input. (c) Left panel: The firing rate trace of a neuron A on the left arm when the animal approaches the choice point. Right panel: The firing rate traces of a pair of neurons when the animal approaches the choice point, with neuron A (red) on the left arm and neuron B (blue) on the right arm. Dashed lines separate theta cycles. (d) Upper panel: The auto-correlogram of the firing rate trace of probe neuron A. Lower panel: The cross-correlogram between the firing rate trace of neuron A and the firing rate trace of neuron B.

Figure 6

Download asset Open asset

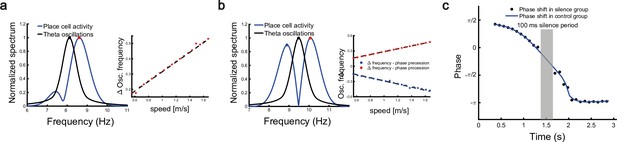
Robust phase coding of position.

(a) Left: normalized spectrum of bump oscillation (black curve) and the oscillation of a unimodal cell (blue curve). Right: linear relationship between the frequency difference and the running speed. (b) Same as (a) but for a bimodal cell. (c) Silencing the network activity for 100 ms (grey shaded area) when the external moving input passes through the center part of the place field of a unimodal cell. Theta phase shifts of the unimodal cell are shown with (black points) or without (blue curve) silencing the network.

Appendix 1—figure 1

Download asset Open asset

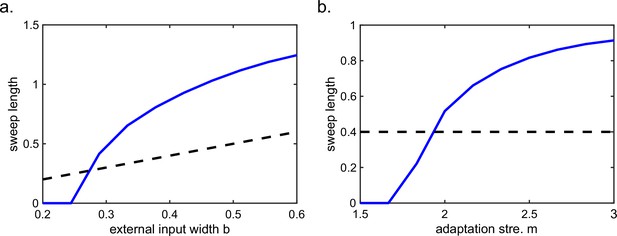
Sweep length is not bounded by the external input width.

(a) The sweep length is positively but not linearly related with the external input width. (b) With fixed external input width, increasing the adaptation strength the sweep length can exceed the external input width. This figure relates to Figure 2 in the main text.

Appendix 1—figure 2

Download asset Open asset

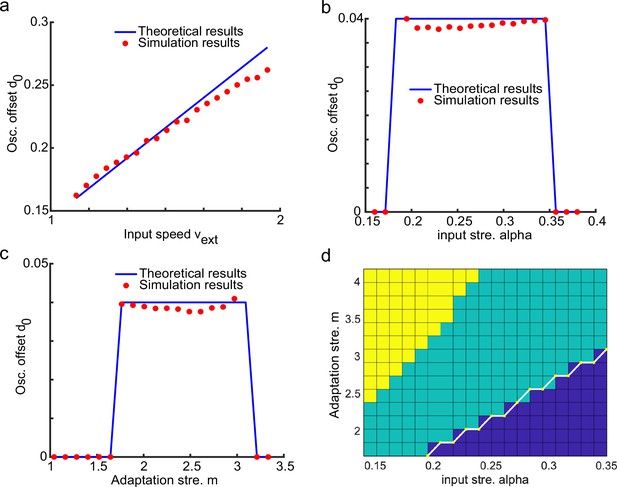
Verifying theoretical results with numerical simulations.

(**a–c**) Simulation results of the average offset $d_{0}$ as a function of $v_{e x t}$ , $α$ , and $m$ , respectively. (d) The phase diagram of network states. The yellow area represents the traveling wave state, the green area represents the oscillatory tracking state, and the blue area represents the smooth tracking state. The white line represents the theoretical boundary given by Equation A85. The parameters used in simulations are: $k = 5$ , $J_{0} = 1$ , $a = 0.4$ , $N = 512$ , $τ = 3$ ms, $τ_{v} = 144$ ms, $ρ = 20.37$ . This figure relates to Figure 2 in the main text.

Appendix 1—figure 3

Download asset Open asset

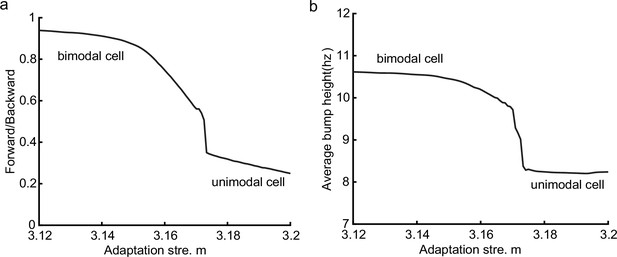
Activity bump height as a function of the adaptation strength.

(a) The ratio between the average bump height during forward window and the average bump height during backward window as function of the adaptation $m$ . When the adaptation strength is relatively small, the mean firing rate of place cells is approximately the same in the forward window as in the backward window. And the place cells exhibit bimodal cell properties. As the adaptation strength gets larger, the mean firing rates in the backward window gradually decrease and the place cells tend to exhibit ﬁring properties more like unimodal cells. (b) The average bump height as a function of the adaptation strength $m$ . Our model predicts that the bimodal cells fire at higher frequency than unimodal cells which can be testable in future experiments. The parameters are: $α = 0.19$ , $k = 5$ , $J_{0} = 1$ , $a = 0.4$ , $N = 512$ , $τ = 3 m s$ , $τ_{v} = 144 m s$ , $ρ = 20.37$ , $v_{e x t} = 0.51 m / s$ . This figure relates to Figure 4 in the main text.

Appendix 1—figure 4

Download asset Open asset

Persistent phase shift with variable silencing periods.

(a) Two examples of the persisting phase shift after transient silencing. Upper panel: The silencing duration is 60 ms. Upper panel: The silencing duration is 275 ms. (b) The phase interval before and after the silencing as a function of the duration of the silencing. The phase interval gradually increases with the silencing duration. The parameters are: $α = 0.19$ , $m = 3.23$ , $a = 0.4$ , $k = 5$ , $J_{0} = 1$ , $N = 512$ , $τ = 3 m s$ , $τ_{v} = 144 m s$ , $ρ = 20.37$ , $v_{e x t} = 1 m / s$ . This figure relates to Figure 6 in the main text.

Appendix 1—figure 5

Download asset Open asset

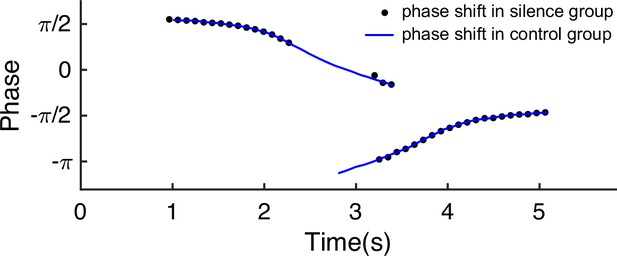
Persistent bimodal phase shift after transient silencing.

The parameters are: $α = 0.19$ , $m = 3.03$ , $a = 0.4$ , $k = 5$ , $J_{0} = 1$ , $N = 512$ , $τ = 3 m s$ , $τ_{v} = 144 m s$ , $ρ = 20.37$ , $v_{e x t} = 0.3 m / s$ . This figure relates to Figure 6 in the main text.

Appendix 1—figure 6

Download asset Open asset

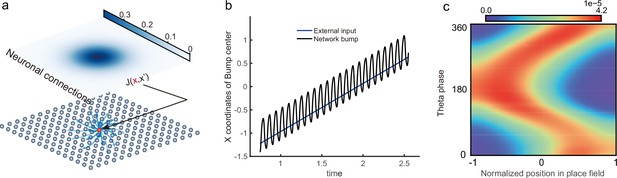
Theta sweeps and theta phase shift in a two-dimensional (2D) continuous attractor neural network (CANN).

(a) A demonstration of the 2D CANN. (b) The trajectory of the bump center and external input center when the input is moving along the x-axis in the 2D CANN. (c) Theta phase as a function of the normalized position of the animal in place field, averaged over all place cells that are placed on the x-axis. –1 represents that the animal just enters the place field, and 1 represents that the animal is about to leave the place field. The parameters are: $α = 0.2$ , $m = 4$ , $k = 6$ , $J_{0} = 1$ , $a = 0.3$ , $N = 16384$ , $τ = 3 m s$ , $τ_{v} = 150 m s$ , $ρ = 415.01$ , $v_{e x t} = 1 m / s$ . This figure relates to Figure 2 in the main text.

Appendix 1—figure 7

Download asset Open asset

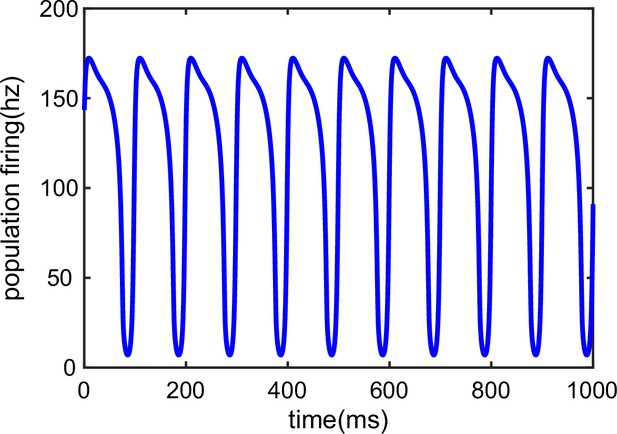
Theta oscillation of the population activities during the theta sweep state.

This figure relates to Figure 4 in the main text.

Appendix 1—figure 8

Download asset Open asset

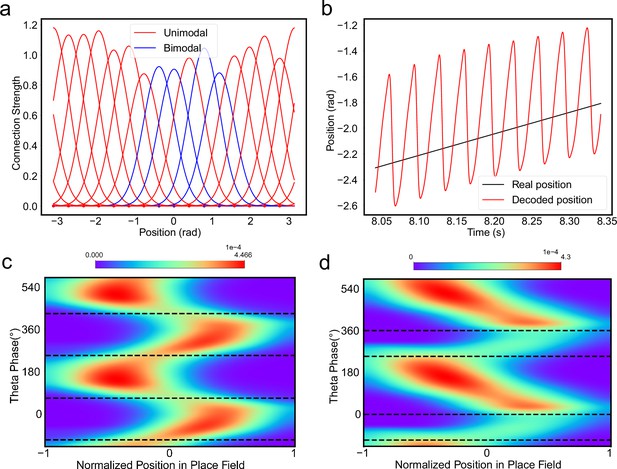
A-continuous attractor neural network (CANN) with heterogeneous connection strength generate oscillatory tracking to account for theta phase shift.

(a) The synaptic connection strength profile of the neurons in the network. The blue lines represent the synaptic strengths of the neurons which turn out to be bimodal neurons, while the red lines represent the unimodal neurons. (b) The oscillatory tracking trajectory of the bump center. (c) The phase shift distribution of the bimodal cells. (d) The phase shift distribution of the unimodal cells. The variations of the connection strength is 0.1, the average value is 1. Other parameters are the same with Figure 3 and Figure 4 in the main text. This figure relates to Figure 4 in the main text.

Appendix 1—figure 9

Download asset Open asset

Oscillatory tracking behavior accounts for theta phase shift with $τ = 10 m s$ .

(a) Oscillatory tracking behavior. (b) Bimodal phase shift of one example neuron. $τ = 10 m s, τ_{v} = 480 m s, α = 0.3, m = 6$ , Other parameters are set equal with the Figure 2 in the main text. This figure relates to Figure 2 in the main text.

Appendix 1—figure 10

Download asset Open asset

Spatiotemporal tracking dynamics when the adaptation strength is low (start from 0).

(a) The tracking behavior when the adaptation strength $m = 0$ ( $α = 0.02$ ). The network bump can generate a bump to track the external input stimuli smoothly but with a constant lagging distance which is proportional to the time constants $τ$ and the external input speed $v_{e x t}$ . (b) The tracking behavior when the adaptation strength $m = 0.1$ ( $α = 0.02$ ). Thanks to the intrinsic mobility introduced by SFA, the network bump anticipatively track the external input stimuli with a contant leading distance which is proportional to the adaptation strength $m$ and the external input speed $v_{e x t}$ . (c) A phase diagram that summarizes the spatiotemporal patterns of the A-CANN tracking behavior. Other parameters are set equal with Figure 2 in the main text. This figure relates to Figure 2 in the main text.

Videos

Video 1

Download asset

posterframe for video — The title of this video is: Three dynamical states of Adaptive Continous Attractor Neural Network.

Video 2

Download asset

Video 3

Download asset

Video 4

Download asset

Tables

Appendix 1—table 1

Commonly used parameter values in the simulation of the linear track environment.

Parameters	Values
Number of place cells: $N$	512
Time constant of neural firing: $τ$	3 ms
Time constant of spike frequency adaptation: $τ_{v}$	144 ms
Neuron density: $ρ$	$256 / π$
Recurrent connection range (Gaussian width): $a$	0.4 m
Width of external input (Gaussian width): $σ$	0.4 m
Recurrent connection strength: $J_{0}$	0.2
Gain factor: $g$	5
Global inhibition strength: $k$	5
Moving speed of the external input: $v_{e x t}$ (m/s)	1.5
Time interval: $δ t$	0.3 s
Simulation duration: $T$	10 s

Appendix 1—table 2

Figure-specific parameter values for input strength $α$ and adaptation strength $m$ .

Figures/parameters	$α$	$m$
An example of smooth tracking (Appendix 1—figure 2c)	0.19	0
An example of traveling wave (Appendix 1—figure 2d)	0	0.31
Intrinsic speed vs. adaptation strength (Appendix 1—figure 2e)	0	0:0.05:0.1
Phase diagram (Appendix 1—figure 2g)	0.05:0.001:0.16	0.9:0.01:1.8
Oscillatory tracking (bimodal) (Appendix 1—figure 4a, e, g)	0.19	3.02
Oscillatory tracking (unimodal) (Appendix 1—figure 4b, f, h)	0.19	3.125

Appendix 1—table 3

Parameters values in the simulation of the T-maze environment.

Parameters	Values
Number of cells central/left/right: $N_{1}, N_{2}, N_{3}$	3000/1500/1500
Time constant of neural firing: $τ$	3 ms
Time constant of spike frequency adaptation: $τ_{v}$	144 ms
Neuron density: $ρ$	${(128 / π)}^{2}$
Recurrent connection range (Gaussian width): $a$	0.3
Recurrent connection strength: $J_{0}$	1.25 ∗ 10^-2
Gain factor: $g$	20
Global inhibition strength: $k$	1.25
Moving speed of the external input: $v_{e x t}$ (m/s)	1.5
Input strength: $α$	2
Adaptation strength: $m$	3.96
Time interval: $δ t$	0.3 s
Simulation duration: $T$	3.3 s

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/87055/elife-87055-mdarchecklist1-v1.docx
Download elife-87055-mdarchecklist1-v1.docx
Source code 1 Modelling code for ‘Firing rate adaptation affords place cell theta sweeps, phase precession, and procession’.: https://cdn.elifesciences.org/articles/87055/elife-87055-code1-v1.zip
Download elife-87055-code1-v1.zip

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Tianhao Chu
Zilong Ji
Junfeng Zuo
Yuanyuan Mi
Wen-hao Zhang
Tiejun Huang
Daniel Bush
Neil Burgess
Si Wu

(2024)

Firing rate adaptation affords place cell theta sweeps, phase precession, and procession

eLife 12:RP87055.

https://doi.org/10.7554/eLife.87055.4

Figures

Theta sequence and theta phase shift of place cell firing.

The network architecture and tracking dynamics.

Oscillatory tracking accounts for theta sweeps and theta phase shift.

Different adaptation strengths account for the emergence of bimodal and unimodal cells.

Constant cycling of future positions in a T-maze environment.

Robust phase coding of position.

Sweep length is not bounded by the external input width.

Verifying theoretical results with numerical simulations.

Activity bump height as a function of the adaptation strength.

Persistent phase shift with variable silencing periods.

Persistent bimodal phase shift after transient silencing.

Theta sweeps and theta phase shift in a two-dimensional (2D) continuous attractor neural network (CANN).

Theta oscillation of the population activities during the theta sweep state.

A-continuous attractor neural network (CANN) with heterogeneous connection strength generate oscillatory tracking to account for theta phase shift.

Oscillatory tracking behavior accounts for theta phase shift with $τ = 10 m s$ .

Spatiotemporal tracking dynamics when the adaptation strength is low (start from 0).

Videos

The title of this video is: Three dynamical states of Adaptive Continous Attractor Neural Network.

The title of this video is: Neuronal activities during bi-directional oscillatory tracking state.

The title of this video is: Neuronal activities during uni-directional oscillatory tracking state.

The title of this video is: Bump oscillation in T-maze environment.

Tables

Commonly used parameter values in the simulation of the linear track environment.

Figure-specific parameter values for input strength $α$ and adaptation strength $m$ .

Parameters values in the simulation of the T-maze environment.

Additional files

MDAR checklist

Source code 1

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Theta sequence and theta phase shift of place cell firing.

The network architecture and tracking dynamics.

Oscillatory tracking accounts for theta sweeps and theta phase shift.

Different adaptation strengths account for the emergence of bimodal and unimodal cells.

Constant cycling of future positions in a T-maze environment.

Robust phase coding of position.

Sweep length is not bounded by the external input width.

Verifying theoretical results with numerical simulations.

Activity bump height as a function of the adaptation strength.

Persistent phase shift with variable silencing periods.

Persistent bimodal phase shift after transient silencing.

Theta sweeps and theta phase shift in a two-dimensional (2D) continuous attractor neural network (CANN).

Theta oscillation of the population activities during the theta sweep state.

A-continuous attractor neural network (CANN) with heterogeneous connection strength generate oscillatory tracking to account for theta phase shift.

Oscillatory tracking behavior accounts for theta phase shift with τ=10ms.

Spatiotemporal tracking dynamics when the adaptation strength is low (start from 0).

The title of this video is: Three dynamical states of Adaptive Continous Attractor Neural Network.

The title of this video is: Neuronal activities during bi-directional oscillatory tracking state.

The title of this video is: Neuronal activities during uni-directional oscillatory tracking state.

The title of this video is: Bump oscillation in T-maze environment.

Commonly used parameter values in the simulation of the linear track environment.

Figure-specific parameter values for input strength α and adaptation strength m.

Parameters values in the simulation of the T-maze environment.

MDAR checklist

Source code 1

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Oscillatory tracking behavior accounts for theta phase shift with $τ = 10 m s$ .

Figure-specific parameter values for input strength $α$ and adaptation strength $m$ .