Figures and data in The interplay between homeostatic synaptic scaling and homeostatic structural plasticity maintains the robust firing rate of neural networks

Figures
Tables
Additional files

9 figures, 8 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

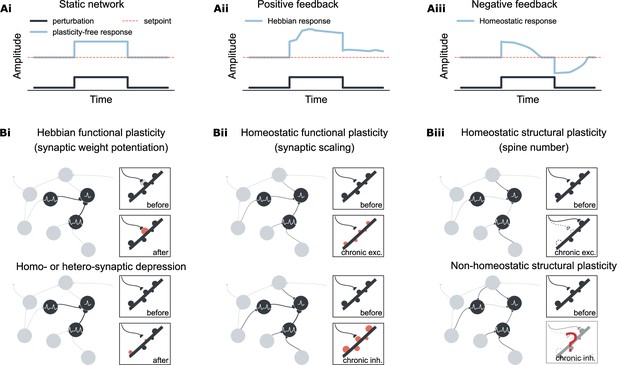
Overview of Hebbian and homeostatic plasticity.

(Ai) In a static network, neural activity is driven by external input. (**Aii**) Hebbian plasticity amplifies network response via a positive feedback mechanism, increasing sensitivity to external input. (**Aiii**) Homeostatic plasticity restores activity toward a setpoint through negative feedback, supporting firing rate homeostasis. (Bi) Hebbian plasticity is synapse-specific, strengthening recurrent connectivity by potentiating the weights of activated synapses. In contrast, synaptic depression can occur either in the same synapse (homosynaptic depression) or in neighboring synapses (heterosynaptic depression) depending on the stimulation protocol. (**Bii**) Homeostatic synaptic scaling is a cell-autonomous process involving proportional up- or down-scaling of all input synaptic weights in response to prolonged changes in postsynaptic activity. (**Biii**) Homeostatic structural plasticity is likewise cell-autonomous and involves compensatory spine loss during chronic excitation. In contrast, chronic inhibition can lead to divergent and sometimes non-homeostatic changes in spine density.

Figure 2

Download asset Open asset

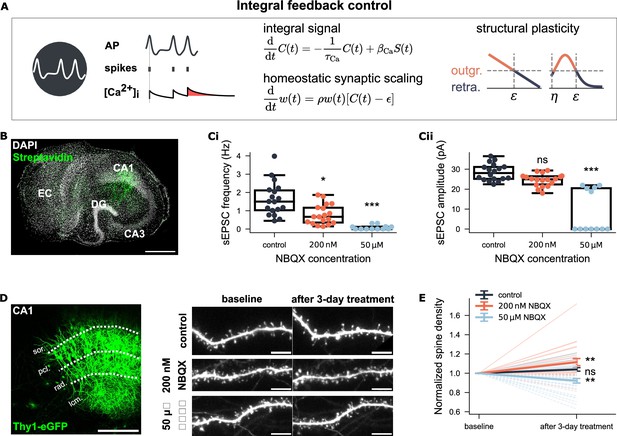
Non-monotonic spine density changes under NBQX inhibition support a biphasic structural plasticity rule.

(A) Integral feedback control framework for homeostatic synaptic scaling and structural plasticity. Both mechanisms use intracellular calcium concentration ( $[C a^{2 +}]_{i}$ , $C (t)$ ) to track neural activity (AP, action potential, $S (t)$ ). Calcium increases with each postsynaptic spike via calcium influx ( $β_{C a}$ ) and decays with a time constant $τ_{C a}$ . Synaptic scaling adjusts synaptic weights $w (t)$ multiplicatively using a scaling factor $ρ$ , based on the deviation of calcium from a setpoint $ϵ$ . Structural plasticity similarly uses $C (t)$ to regulate the growth and retraction of axonal boutons and dendritic spines. Two variants of the structural plasticity rule are illustrated: one with a linear and the other with a non-linear (biphasic) calcium dependency. (B) Example CA1 pyramidal neuron recorded and *post hoc* identified in an entorhinal-hippocampal tissue culture. Scale bar: 500 μm. (**Ci-Cii**) Group data of AMPA receptor-mediated sEPSC from three experimental groups (control: N=18; 200 nM NBQX: N=18; 50 μM NBQX: N=12). (D) Representative Thy1-eGFP culture and time-lapse imaging of dendritic segments in the stratum radiatum (rad.) before and after three-day treatment. Scale bars: 200 μm, 5 μm. (E) Spine density at baseline and after treatment. Values are normalized to the respective baseline per segment. Light-shaded lines show individual trajectories (solid = increase; dashed = decrease). Dark-shaded lines with error bars represent group means and SEM for each group (control: N=19; 200 nM NBQX: N=24; 50 μM NBQX: N=33).

Figure 3 with 1 supplement

Download asset Open asset

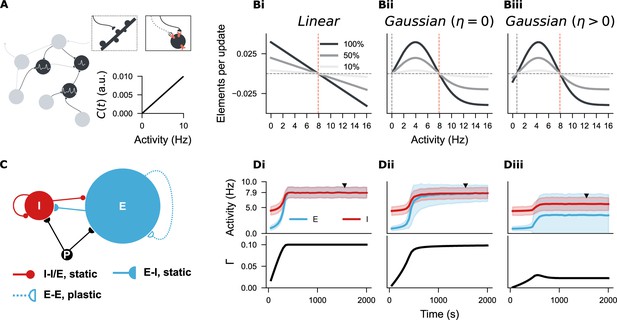
Establishing a spiking neural network with three distinct structural plasticity rules.

(A) A network of point neurons was used to study structural plasticity. Dendritic spines are visualized as pink sticks on the soma, and axonal boutons are represented by half-circles–––solid or empty depending on their growth state. An empty half-circle with a dashed line denotes a retracting axon. In this model, intracellular calcium concentration $C (t)$ is linearly correlated with neural firing rate, so neural activity is used throughout this study as a proxy for ‘firing rate homeostasis’, given its physical unit compared to the arbitrary unit (a.u.) of calcium concentration. (**Bi-Biii**) Three structural plasticity growth rules regulate changes in synaptic element numbers. (Bi) Linear rule with a single setpoint ( $ϵ = 7.9$ , orange line). (**Bii**) Gaussian rule with two setpoints, one at zero ( $η = 0$ , grey line; $ϵ = 7.9$ , orange line). (**Biii**) Gaussian rule with two non-zero setpoints ( $η = 0.7$ , grey line; $ϵ = 7.9$ , orange line). Three shades represent 100%, 50%, or 10% of the original growth rate ( $ν$ ), with positive and negative values indicating the rate of synaptic element growth and loss, respectively. (C) Network architecture based on the Brunel network model, consisting of 10000 excitatory (E, blue) and 2500 inhibitory neurons (I, red), receiving external Poisson input (P). Synapses among I-I, I-E, and E-I populations are hard-wired with a fixed 10% probability. E-E synapses are subject to structural plasticity rules. (**Di-Diii**) Temporal evolution of neural activity and network connectivity ( $Γ$ ) during network growth, guided by the three plasticity rules. Unless otherwise stated, the curves and shaded areas represent the mean and standard deviation of firing rates in E and I populations. An equilibrium state ( $Γ = 10 %$ ) was reached under the linear and zero-Gaussian rules (**Di, Dii**), but not with the biphasic Gaussian rule (**Diii**). Firing rate distributions and network connectivity matrices at the marked time points (solid triangles) are shown in Figure 3—figure supplement 1 for **Di-Dii**, and in Figure 4 for **Diii**.

Figure 3—figure supplement 1

Download asset Open asset

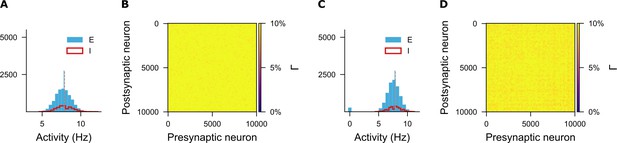
Firing rate distributions and connectivity matrices at the corresponding time points shown in Figure 3.

Panels A and B show results for the linear growth rule; panels C and D for the *zero Gaussian rule* ( $η = 0$ ).

Figure 4

Download asset Open asset

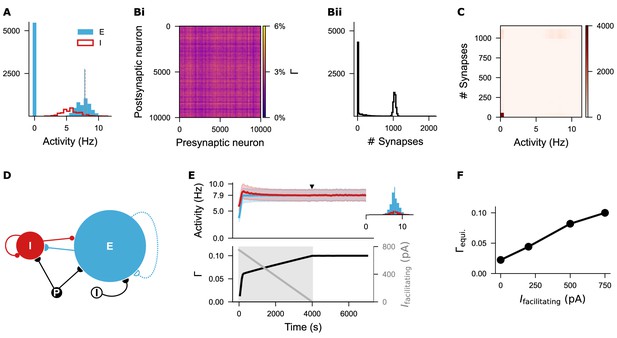
Silent neurons remain isolated under the biphasic Gaussian rule.

(A) Histogram of firing rates for excitatory and inhibitory neurons sampled at the time point indicated in Figure 3Diii. Nearly half of the excitatory neurons remained silent. The blue vertical line marks the mean firing rate of non-silent excitatory neurons, while the orange dashed line indicates the target firing rate ( $ϵ = 7.9 H z$ ). (**Bi-Bii**) Network connectivity matrix and distribution of synapse numbers across individual excitatory neurons. (C) Correlation heatmap showing the relationship between neural activity and synapse number per excitatory neuron. Silent neurons failed to form synapses, whereas active neurons fired around the target rate and formed approximately 1000 synapses with other active excitatory neurons. (D) Network architecture after introducing a damping facilitating current ( $I_{f a c i l i t a t i n g}$ ) to promote network development. (E) Temporal dynamics of firing rate (mean and standard deviation) and network connectivity after current injection. The inset displays firing rate distributions for excitatory and inhibitory neurons at the time point indicated by the solid triangle. The facilitating current started at 750 pA and decayed linearly to zero over 4000 s. (F) Different initial amplitudes of the facilitating current led to distinct levels of network connectivities. An initial value of 750 pA was used consistently throughout the study.

Figure 5

Download asset Open asset

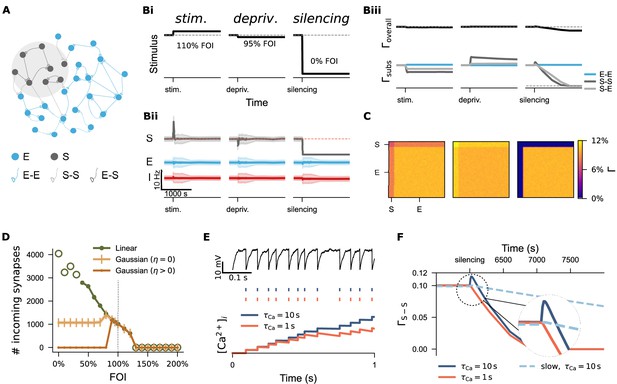
Divergent regulation of network connectivity under stimulation and deprivation via three structural plasticity rules.

(A) A subpopulation (S) comprising 10% excitatory neurons (E) was subject to activity perturbation. All E-E, S-S, and E-S synapses were governed by the biphasic Gaussian rule. (Bi) Activity perturbation protocol. Three levels of input intensity, expressed as a percentage of the original Poisson input (fold of intensity, FOI), were used: *stimulation* (110% FOI), *mild deprivation* (95% FOI), and *silencing* (0% FOI). (**Bii**) Temporal dynamics of mean firing rates and standard deviation for the S, E, and inhibitory population (I) under each protocol. (**Biii**) Temporal evolution of overall network connectivity ( $Γ_{o v e r a l l}$ ) and subpopulation-specific connectivity ( $Γ_{s u b s}$ ) under each condition. Due to the symmetric application of plasticity rules to spines and boutons, the connection probabilities from E to S and S to E are equivalent. Therefore, only S-E traces are shown unless otherwise noted. (C) Final network connectivity matrices following stimulation, mild deprivation, or silencing. (D) Average number of incoming synapses to neurons in S subpopulation across a range of FOIs. Empty green circles indicate values from networks exposed to extreme stimulation or inhibition, where both activity and network connectivity were unstable. (E) Examples of two neurons receiving identical external input but with different calcium decay time constants ( $τ_{C a}$ ). The upper panel shows membrane potential traces; the middle panel displays spike trains, and the lower panel illustrates integrated calcium concentration over time. (F) Connectivity trajectories of silenced subnetwork under three different conditions. The dashed circle highlights a region shown at higher magnification.

Figure 6

Download asset Open asset

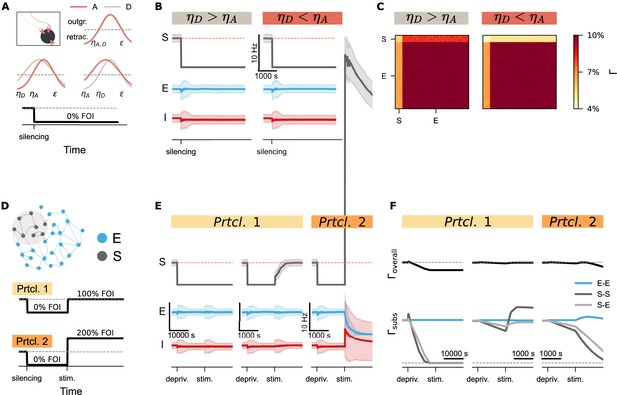
Activity perturbation and recurrent connectivity jointly shape the evolution of network connectivity.

(A) Structural plasticity rules applied to both axonal boutons (A, light brown curve) and dendritic spines (D, pink curve), using identical growth functions with $η_{A} = η_{D}$ (upper inset). Variations with asymmetric parameters (different $η$ values could be used for axonal and dendritic elements, such as $η_{A} > η_{D}$ or $η_{A} < η_{D}$ ) are conceptually possible. A silencing protocol was implemented using a fold of original input intensity (FOI). (B) Temporal dynamics of neural activity (mean and standard deviation) for the silenced subpopulation (S), excitatory neurons (E), and inhibitory neurons (I) under two different conditions. (C) Final network connectivity matrices at the end of the silencing protocol under the same two conditions shown in B. (D) Experimental protocols used to assess the combined effects of recurrent connectivity and external stimulation. External stimulation was introduced to the deprived subnetwork under conditions of varying recurrent connectivity. In Protocol 2 (Prtcl. 2), the external stimulation intensity was doubled relative to Protocol 1 (Prtcl. 1). The same structural plasticity rule was applied to both axonal and dendritic elements ( $η_{A} = η_{D}$ ). (E) Temporal trajectories of neural activity (mean and standard deviation) following silencing and external stimulation. The network in the left panel was simulated with a structural growth rate 10 times faster than that in the middle and right panel, resulting in lower recurrent connectivity. (F) Corresponding evolution of overall connectivity ( $Γ_{o v e r a l l}$ , top) and subnetwork-specific connectivity ( $Γ_{s u b s}$ , bottom) for excitatory-excitatory (E–E), subpopulation (S–S), and cross-population (S–E) connections.

Figure 7 with 1 supplement

Download asset Open asset

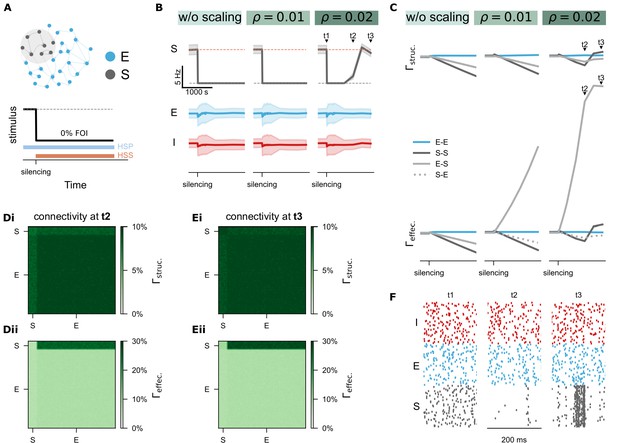
Homeostatic synaptic scaling (HSS) shapes effective connectivity and interacts with homeostatic structural plasticity (HSP).

(A) Protocol of silencing (0% FOI) was applied to a subpopulation of excitatory neurons (S) and synaptic scaling was activated with three different strengths: $ρ = 0$ (no scaling), $ρ = 0.01$ (weak scaling), and $ρ = 0.02$ (strong scaling). (**B-C**) Time courses of network activity (mean and standard deviation) and network connectivity. $Γ_{s t r u c .}$ denotes structural connectivity and $Γ_{e f f e c .}$ refers to effective connectivity. (**Di-Dii**) Structural and effective connectivity matrices of the entire network at time point $t 2$ . (**Ei-Eii**) Structural and effective connectivity matrices at time point $t 3$ . (F) Raster plots of spiking activity for 100 representative neurons at the time points $t 1$ , $t 2$ , and $t 3$ , including inhibitory (I, red), excitatory (E, blue), and silenced excitatory neurons (S, grey).

Figure 7—figure supplement 1

Download asset Open asset

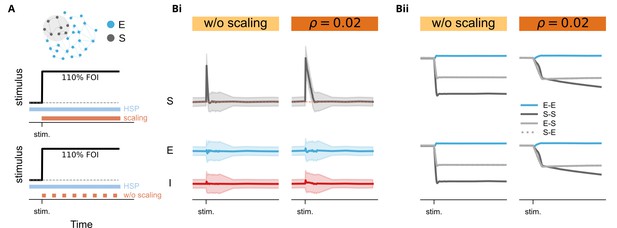
Time courses of network activity (Bi), structural connectivity (Bii, upper panels), and effective connectivity (Bii, lower panels) under the stimulation protocol, with and without the homeostatic synaptic scaling rule.

A scaling factor of $ρ = 0.02$ was applied, and stimulation was delivered at 110% FOI (fold of the original intensity).

Figure 8 with 1 supplement

Download asset Open asset

Spine size analysis suggests interactions between functional and structural plasticity.

(A) Activity trajectories and average incoming excitatory synaptic weights of two representative excitatory neurons: one from the deprived subpopulation (N1, grey) and one from the non-deprived group (N2, blue). The gray dashed line in the upper panel indicates the target activity setpoint. Shaded areas represent the standard deviation of incoming synaptic weights. Synapses were categorized based on their source: from the deprived subpopulation (S, grey) or from non-deprived excitatory neurons (E, blue). Triangles in the middle panel indicate the time points used for synaptic weight distribution analyzed in B. (B) Distributions of synaptic weights for neuron N1 *before* and *after* activity deprivation. Numbers above the plots indicate the total synapse count per source type at each time point. (C) Normalized synapse numbers over time of neuron N1 (solid line) and the averaged across all deprived neurons (dashed line). (Di-Diii) Baseline spine size distributions for three groups: control (N=489), 200 nM-NBQX treated (N=736), and 50 μM-NBQX treated (N=675). (E) Cumulative distribution functions (cdf) of spine sizes before and after the three-day treatment. The inset shows average normalized spine sizes across conditions. (F) Normalized spine size changes grouped by initial spine size. The $x$ -axis denotes the upper limit of each bin. Data points above the dashed line represent spine enlargement; points below indicate shrinkage. Error bars in the inset of E and in F represent SEM for each group.

Figure 8—figure supplement 1

Download asset Open asset

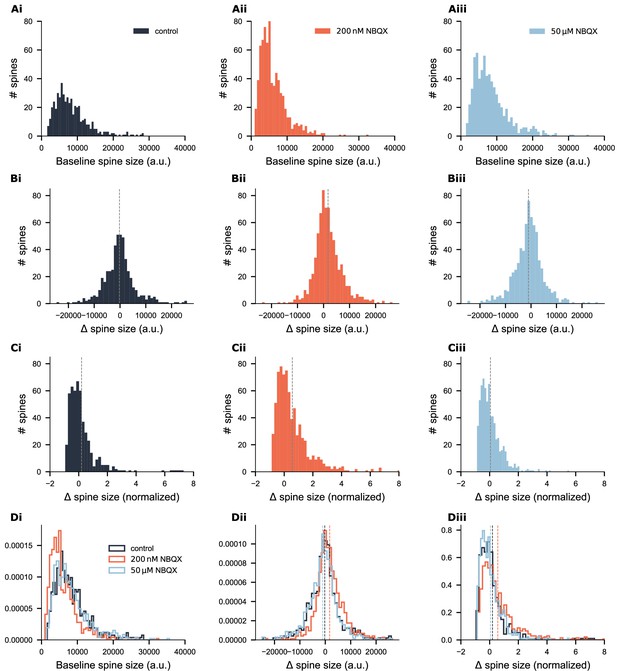
Distributions of baseline spine sizes and spine size changes over the three-day treatment period across all three groups.

(A) Distributions of baseline spine sizes prior to treatment. (**B-C**) Distributions of absolute spine size changes and size changes normalized to initial spine size, respectively. Vertical lines indicate group mean values. (D) Probability density functions summarizing the corresponding values across all groups. Colored vertical lines indicate the mean for each group.

Figure 9 with 3 supplements

Download asset Open asset

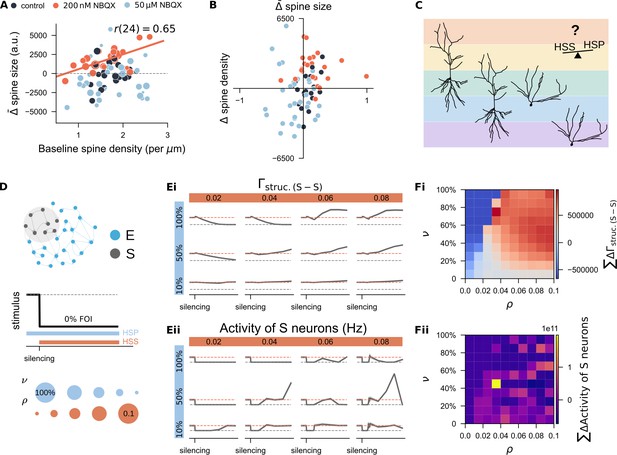
Systematic study of the interaction between homeostatic synaptic scaling and structural plasticity in response to activity silencing.

(A) Correlation between each dendritic segment’s average change in spine size and its initial spine density. Marker size reflects the net change in spine density over the three-day period. (B) Correlation between each dendritic segment’s average changes in spine size and its change in spine density. (C) Conceptual hypothesis: Different combinations of homeostatic synaptic scaling (HSS) and homeostatic structural plasticity (HSP) may form a spectrum, allowing individual neuron types or even distinct dendritic segments within the same neuron to be governed by unique rule combinations. This framework could account for the variability observed in experimental studies of structural plasticity. Sample neuron reconstructions are based on CA1 pyramidal cells (left two) and dentate gyrus granule cells (right two) recorded in our lab. (D) Simulation protocol used to explore the interaction between homeostatic synaptic scaling and structural plasticity. The growth rate of the HSP rule ( $ν$ ) and the strength of the HSS rule ( $ρ$ ) were systematically varied. (**Ei-Eii**) Example time course of structural connection probability and neural activity in the deprived subpopulation (S) under selected combinations of ( $ν$ ) and ( $ρ$ ). (**Fi-Fii**) Quantification of deviations in connectivity and firing rate under different parameter combinations. Deviations were computed as the area between the actual trajectory and either the equilibrium connection probability (10%) or the target firing rate ( $ϵ$ ) over the silencing period. Results represent the mean from 11 independent trials.

Figure 9—figure supplement 1

Download asset Open asset

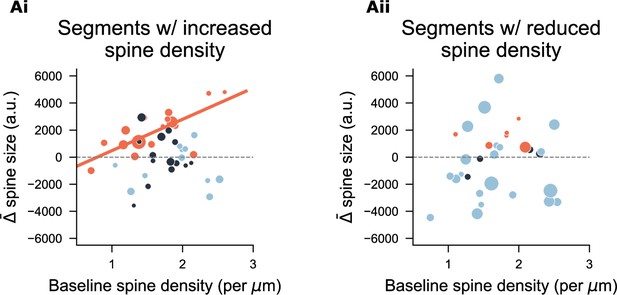
Relationship between average spine size change and initial spine density for individual dendritic segments.

This figure expands on Figure 2G by categorizing segments based on whether spine density increased or decreased over the 3-day treatment. Marker size indicates the net change in spine density. A significant positive correlation was observed in the 200 nM NBQX-treated group for segments with increased density ( $r (18) = 0.74$ , $p = 0.0005$ , Pearson’s correlation).

Figure 9—figure supplement 2

Download asset Open asset

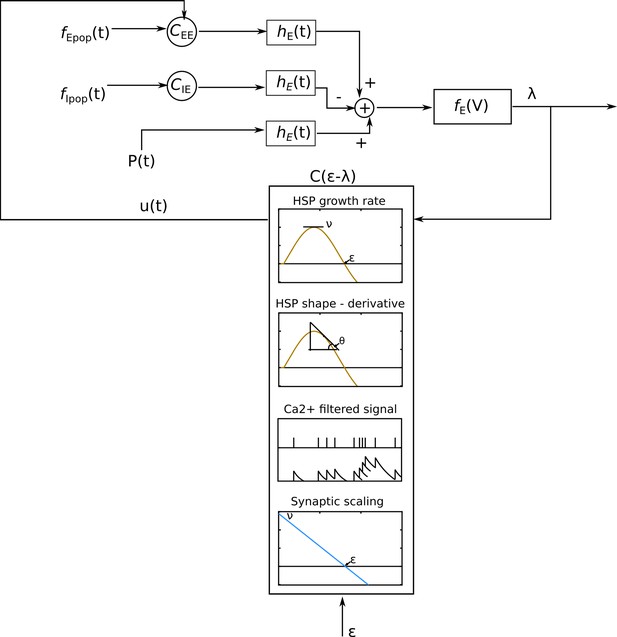
Schematic representation of the plasticity rules used in this study, framed within a control theory perspective.

In the diagram, $h_{E} (t)$ denotes the transfer function of synaptic inputs to an excitatory neuron E, whose dynamics are described by $f_{E} (V)$ , where $V$ is the membrane potential. The connectivity matrices $C_{E E}$ and $C_{I E}$ represent synaptic connections within an excitatory population $f_{E p o p}$ and from an inhibitory population $f_{I p o p}$ , respectively. $P (t)$ indicates Poissonian input noise representing external network activity not explicitly modeled. The error between the neuron’s instantaneous firing rate $λ$ and a predefined target rate $ϵ$ serves as the control signal for the homeostatic structural plasticity and synaptic scaling mechanisms, implemented as a controller $C$ , which generates an output signal $u (t)$ governs the rate of synaptic element creation or deletion and modulates the excitatory connectivity matrix $C_{E E}$ . While $u (t)$ is not a synaptic element itself, it reflects the error signal processed via calcium dynamics as a proxy for firing rate. Due to the Gaussian-like shape of the structural plasticity rule, $u (t)$ also depends on the rate of change in synaptic element turnover. The slope of the structural rule critically influences the stability of the system and its ability to converge toward a network configuration that supports the target firing rate. Collectively, the plasticity mechanisms function analogously to a proportional-integral-derivative (PID) controller.

Figure 9—figure supplement 3

Download asset Open asset

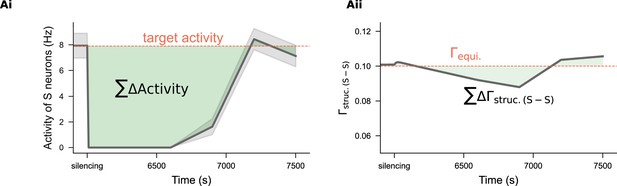
Quantification of $Δ A c t i v i t y$ in S neurons and $Δ Γ_{s t r u c . (S - S)}$ used to generate the heatmap shown in Figure 8E and F.

Orange lines indicate the target values for firing rate and structural connectivity. Discrepancies from these targets were computed and integrated over several time steps following the onset of the silencing protocol.

Tables

Key resources table

Reagent type (species) or resource	Designation	Source or reference	Identifiers	Additional information
Strain, strain background (mice)	C57BL/6 J mouse	Jackson Laboratory	RRID:IMSR_JAX:000664
Strain, strain background (mice)	Thy1-eGFP mouse	Jackson Laboratory	RRID:IMSR_JAX:007788
Peptide, recombinant protein	Streptavidin*	Invitrogen	Cat#: S32354 RRID:AB_2315383	Post hoc labeling (1:1000)
Chemical compound, drug	Paraformaldehyde (PFA)	Carl Roth	Cat#: 0335.3	Final concentration: 4% (w/v) in PB or PBS
Chemical compound, drug	NBQX	Tocris Bioscience	Cat#: 1044	Final concentrations: 200 nM and 50 µM
Chemical compound, drug	DAPI (1 mg/ml in water)	Thermo Fisher Scientific	Cat#: 62248	Post hoc labeling (1:2000)
Software, algorithm	Python	Python Software Foundation	RRID:SCR_008394
Software, algorithm	NEST simulator	NEST Initiative	RRID:SCR_002963
Software, algorithm	Clampfit^†	Molecular Devices	RRID:SCR_011323
Software, algorithm	Image J	NIH ^‡	RRID:SCR_003070
Software, algorithm	Prism (Graphpad)	GraphPad Software	RRID:SCR_002798
Other	OCT ^§	Method described in Del Turco and Deller, 2007	N/A

*

Alexa Fluor 488-Conjugate.
†

pClamp software package.
‡

National Institutes of Health.
§

Organotypic entorhinal-hippocampal tissue cultures.

Table 1

Parameters for the point neuron model.

$τ_{m}$	$t_{r e f}$	$V_{0}$	$V_{r e s e t}$	$V_{t h}$	$C_{m e m}$
$20.0 m s$	$2.0 m s$	$0.0 m V$	$10.0 m V$	$20.0 m V$	$250 p F$

Table 2

Parameters for the network model.

$N_{E}$	$N_{I}$	$Γ_{E - I}$	$Γ_{I - E}$	$Γ_{I - I}$	$J_{E}$	$J_{I}$	$r_{e x t}$
10000	2500	10%	10%	10%	$0.1 m V$	$- 0.8 m V$	$30 k H z$

Varied values for r_ext were used for activity perturbation.

Table 3

Parameters for the linear structural plasticity model.

$ϵ$	$ν$	$τ_{C a}$	$β_{C a}$
0.0079	0.00395 s⁻¹	10 s	0.0001

Table 4

Parameters for the zero Gaussian structural plasticity model.

$ϵ$	$η$	$ν$	$τ_{C a}$	$β_{C a}$
0.0079	0	0.004 s⁻¹	10 s	0.0001

Table 5

Parameters for the biphasic Gaussian structural plasticity model.

$ϵ$	$η$	$ν$	$τ_{C a}$	$β_{C a}$
0.0079	0.0007	0.004 s⁻¹	10 s	0.0001

Table 6

Parameters for the synaptic scaling model.

$ϵ$	$ρ$
0.0079	[0, 0.1]

Table 7

Protocols for numeric stimulation.

	plasticity rules	$η$	growth rate	$I_{f a c i l i t a t i n g}$	FOI	$τ_{C a}$	$ρ$
Figure 3Bi, Di	linear	-	100%, 50%, 10%			10 s	-
Figure 3Bii, Dii	Gaussian	0	100%, 50%, 10%			10 s	-
Figure 3Biii, Diii	Gaussian	0.0007	100%, 50%			10 s	-
Figure 4A-C	Gaussian	0.0007	100%	750 pA		10 s
Figure 4E	Gaussian	0.0007	100%	750 pA		10 s	-
Figure 4F	Gaussian	0.0007	100%	0, 200, 500, 750 pA		10 s	-
Figure 5B and C	Gaussian	0.0007	100%	750 pA	110%,95%, 0%	10 s	-
Figure 5D	Gaussian	0.0007	100%	750 pA	[0%, 200%]	10 s	-
Figure 5E	-	-	-	-	-	1 s, 10 s	-
Figure 5F, orange	Gaussian	0.0007	100%	750 pA	0%	1 s	-
Figure 5F, dark blue	Gaussian	0.0007	100%	750 pA	0%	10 s	-
Figure 5F, light blue	Gaussian	0.0007	10%	750 pA	0%	10 s	-
Figure 6B and C	Gaussian	0.0007 for D,0.0004 or0.001 for A	10%	750 pA	0%	10 s	-
Figure 6E and F	Gaussian	0.0007	10%, 100%	750 pA	0% to100% or0% to200%	10 s	-
Figure 7B–F	Gaussian +scaling	0.0007	10%	750 pA	0%	10 s	0, 0.01, 0.02
Figure 8C–F	Gaussian +scaling	0.0007	[0%, 100%]	750 pA	0%	10 s	[0, 0.1]

The column FOI summarizes the percentages of original intensities used for external activity perturbation.
For Figure 5D, FOI values ranging from 0% to 200% were used for the systematic study.
Figure 5E was performed in a single neuron model without any plasticity.

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/88376/elife-88376-mdarchecklist1-v1.pdf
Download elife-88376-mdarchecklist1-v1.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Han Lu
Sandra Diaz-Pier
Maximilian Lenz
Andreas Vlachos

(2025)

The interplay between homeostatic synaptic scaling and homeostatic structural plasticity maintains the robust firing rate of neural networks

eLife 12:RP88376.

https://doi.org/10.7554/eLife.88376.3

Share this article

Cite this article

Overview of Hebbian and homeostatic plasticity.

Non-monotonic spine density changes under NBQX inhibition support a biphasic structural plasticity rule.

Establishing a spiking neural network with three distinct structural plasticity rules.

Firing rate distributions and connectivity matrices at the corresponding time points shown in Figure 3.

Silent neurons remain isolated under the biphasic Gaussian rule.

Divergent regulation of network connectivity under stimulation and deprivation via three structural plasticity rules.

Activity perturbation and recurrent connectivity jointly shape the evolution of network connectivity.

Homeostatic synaptic scaling (HSS) shapes effective connectivity and interacts with homeostatic structural plasticity (HSP).

Time courses of network activity (Bi), structural connectivity (Bii, upper panels), and effective connectivity (Bii, lower panels) under the stimulation protocol, with and without the homeostatic synaptic scaling rule.

Spine size analysis suggests interactions between functional and structural plasticity.

Distributions of baseline spine sizes and spine size changes over the three-day treatment period across all three groups.

Systematic study of the interaction between homeostatic synaptic scaling and structural plasticity in response to activity silencing.

Relationship between average spine size change and initial spine density for individual dendritic segments.

Schematic representation of the plasticity rules used in this study, framed within a control theory perspective.

Quantification of ΔActivity in S neurons and ΔΓstruc.(S−S) used to generate the heatmap shown in Figure 8E and F.

Parameters for the point neuron model.

Parameters for the network model.

Parameters for the linear structural plasticity model.

Parameters for the zero Gaussian structural plasticity model.

Parameters for the biphasic Gaussian structural plasticity model.

Parameters for the synaptic scaling model.

Protocols for numeric stimulation.

MDAR checklist

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Quantification of $Δ A c t i v i t y$ in S neurons and $Δ Γ_{s t r u c . (S - S)}$ used to generate the heatmap shown in Figure 8E and F.