Inferring control objectives in a virtual balancing task in humans and monkeys
- Department of Biology, Northeastern University, United States
- Department of Electrical and Computer Engineering, Northeastern University, United States
- Department of Mechanical Engineering, Northern Arizona University, United States
- Institute for Experiential Robotics, Northeastern University, United States
- Department of Bioengineering, and Center for the Neural Basis of Cognition, University of Pittsburgh, United States
- Department of Physics, Northeastern University, United States
Figures
Figure 1
Experimental setup for monkeys and humans performing the CST.
Monkeys (A) and humans (B) controlled an unstable cursor displayed on a screen using lateral movements of their right hand. The hand movements were recorded using motion capture; the data were used in real-time to solve for the cursor position and velocity through the CST dynamics equation. Timeseries of the hand (red) and cursor (blue) movements shown for four example trials from monkeys (C) and humans (D).
Figure 2
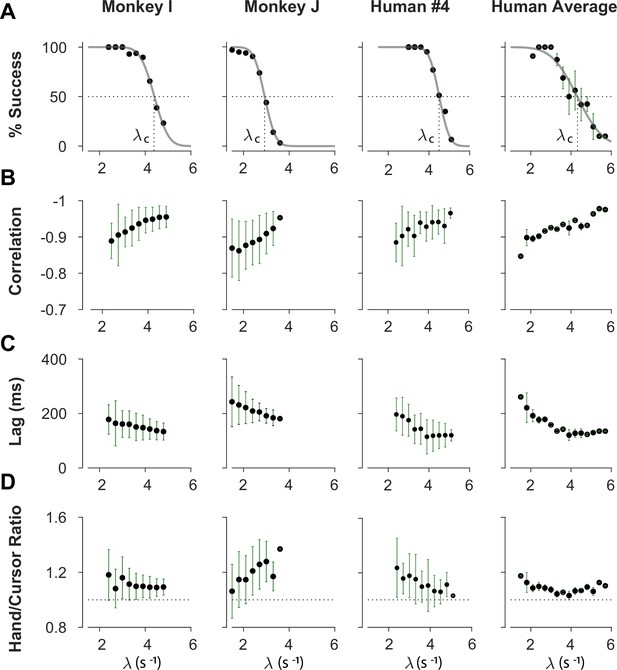
Overall behavioral characteristics of CST performance as a function of task difficulty ().
Data is shown for two individual monkeys (first two columns from left) from a previous study (Quick et al., 2018), as well as an example human individual (third column from left) and the average across human subjects (right-most column; n=6). For the individual subjects, each data point and its corresponding error bars represent the mean ± SD across trials for any given difficulty level, respectively. For the human average plot, the data points and their corresponding error bars represent the mean ± SE across individuals for each difficulty level. (A) Psychometric curves for success rate (%) as a function of task difficulty (). The difficulty level at which the success rate crossed 50% was considered as the critical stability point (), indicating the individual’s skill level in task. (B) Correlation between the hand and cursor position trajectories during CST. (C) Sensorimotor lag between the cursor and the hand movements. (D) Ratio of hand RMS over the cursor RMS calculated for each trial, representing the strength of the hand response relative to the cursor displacement.
Figure 3
A generative model to perform the CST.
(A) An optimal feedback controller generates motor commands based on two control objectives, position and velocity control. The motor command leads the movement of the effector (hand), which performs the CST. The cursor position and velocity are provided as feedback from which all the states are estimated and fed back to the controller. (B, C) Example trials simulated under the two control objectives for different difficulty levels: keeping the cursor at the center (B; Position Control) and keeping the cursor still (C; Velocity Control).
Figure 4
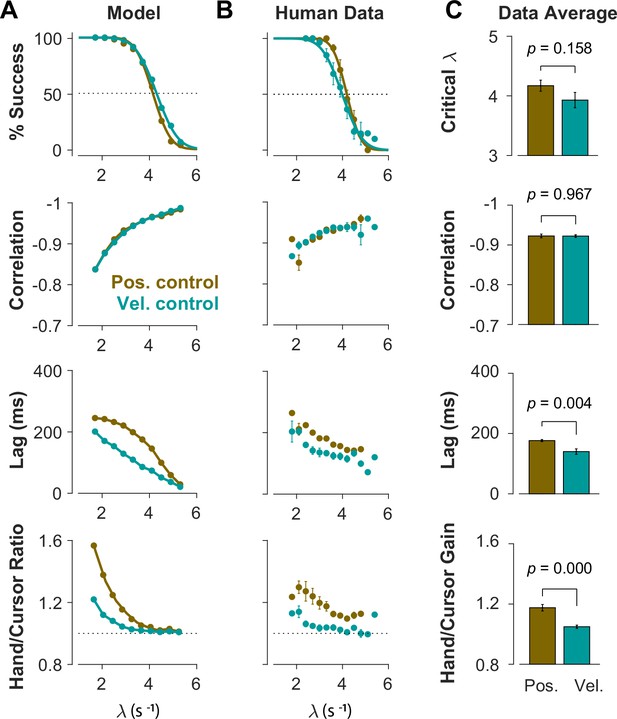
Different control objectives result in measurably different behavior.
Overall performance of the model (A) and human subjects (B) for two control objectives, Position Control and Velocity Control. The four rows show success rate (first row), correlation between hand and cursor position (second row), sensorimotor lag between cursor and hand position (third row), and the hand/cursor RMS ratio, defined as the RMS of hand movement over the RMS of cursor movement during each trial (last row). The error bars on the human average data indicate the standard error of the mean across subjects for each group (n=6 per group). (C) The average performance across difficulty levels and subjects within each group. The critical (first row) indicates the difficulty level at which the success rate crosses 50%. The p-values are produced using unpaired t-test.
Figure 5
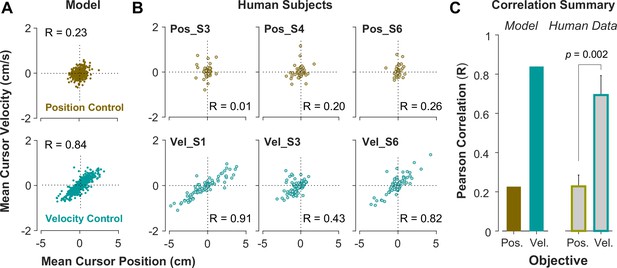
State-space distribution of trials reveals different control strategies.
(A) Mean cursor velocity plotted against mean position for each trial, shown for the position control objective (top) and velocity control objective (bottom). Each data point represents one successful trial and was simulated for a range of difficulty levels up to the critical value (corresponding to 50% success rate). (B) Three example human subjects from the position control group (top row) and velocity control group (bottom row). Each data point represents one successful trial. The data represents an ensemble of trials ranging in difficulty levels up to the critical value for each subject. R indicates the correlation between the trial position and velocities. (C) Pearson correlation coefficient between cursor mean position and velocity for each control objective in the model (left) and human data (right). The human data shows the mean (± SE) across subjects for each control objective group (n=6 per group). The p-value is produced using an unpaired t-test.
Figure 6
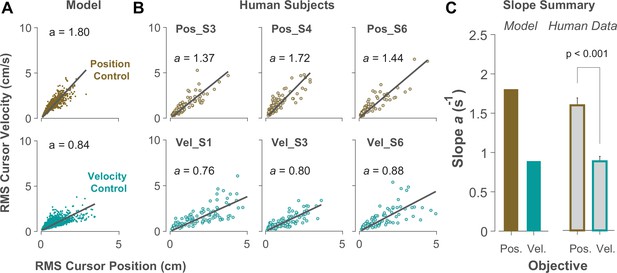
Identifying control objective based on magnitude of cursor movement in the state space.
(A) Magnitude of cursor movements quantified by the RMS of position and cursor velocity for each trial, plotted against each other; position control objective (top) and velocity control objective (bottom). Each data point represents one successful trial and was generated based on the model simulations for a range of difficulty levels up to the critical value (corresponding to 50% success rate). (B) Performance of three example subjects from the position control group (top row) and velocity control group (bottom row). Each data point represents one successful trial. The data represents an ensemble of trials ranging in difficulty level up to the critical value for each subject. The values of the regression slopes are also shown. (C) Summary of the regression slopes for the RMS plots, shown for each control objective in the model (left) and human data (right). The human data shows the mean (± SE) across subjects for each control group (n=6 per group). The p-value is produced using an unpaired t-test.
Figure 7
Classifying control objectives in humans who received explicit instructions.
(A) Simulated data in the RMS space of cursor movement used as training set for a classifier to determine the control objective of each trial. (B) Data from three example subjects in each group, where each trial was classified as Position Control (brown), Velocity Control (cyan), or Uncertain as to the control objective (grey). To obtain the control objective of each trial, the classifier (a support vector machine; see Methods) obtained the probability of that trial performed with Position Control, where P(pos)>95% was classified as Position Control, P(pos)<5% was classified as Velocity Control, and everything else was classified as uncertain. The average of P(pos) across all trials for each individual is shown inside the respective plot. (C) Overall probability of Position Control summarized for all subjects instructed in the position and Velocity Control groups of Experiment 2.
Figure 8
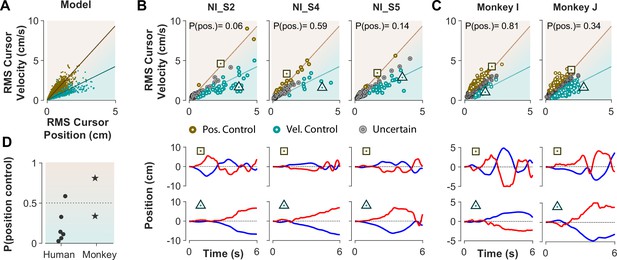
Inferring control strategies in monkeys and humans who received no instructions.
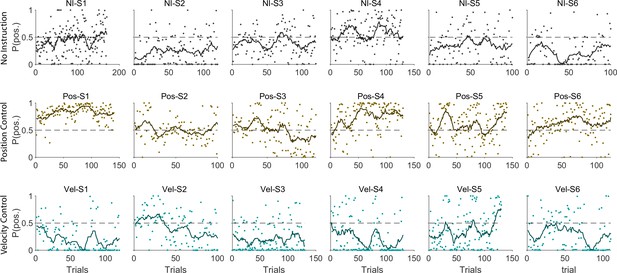
(A) Simulated data in the RMS space of cursor movement was used as training set for a classifier to determine the control objective of a trial without explicit instructions. (B) Data from three example human subjects with no instructions (NI) about the control objective. Each trial (data point) is classified based on the probability of Position Control, P(pos), obtained for each trial from the classifier. Trials with P(pos) >95% and P(pos) <5% were, respectively, labeled as Position Control (brown) and Velocity Control (cyan), while other probabilities were labeled as Uncertain (grey). Two example trials, one from each control objective, are shown in the bottom row. (C) The classifier was used on data from two monkeys (Monkey I and J) who performed the CST. Similarly, trials for each monkey were categorized as Position Control (brown), Velocity Control (cyan), or Uncertain (grey). (D) Overall probability of an individual preferring Position Control, shown for six humans and two monkeys. This measure was obtained for each individual as the average probability of Position Control across all trials.
Appendix 1—figure 1
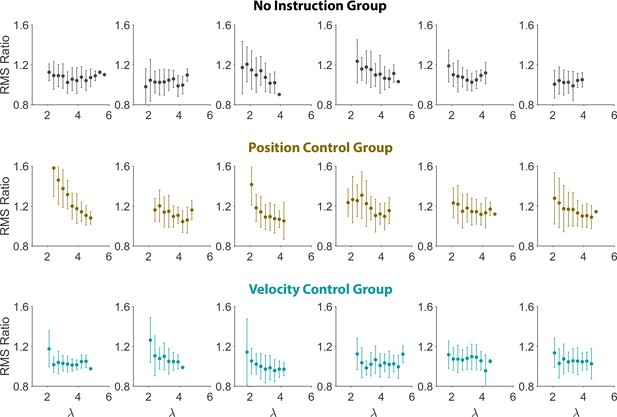
Hand/Cursor RMS ratio for individual participants in all three groups (n=6 per group):.
Top: No Instruction group, Middle: Position Control group, and Bottom: Velocity Control group. The error bars indicate the standard deviations (SD) across trials for each difficulty level.
Appendix 1—figure 2
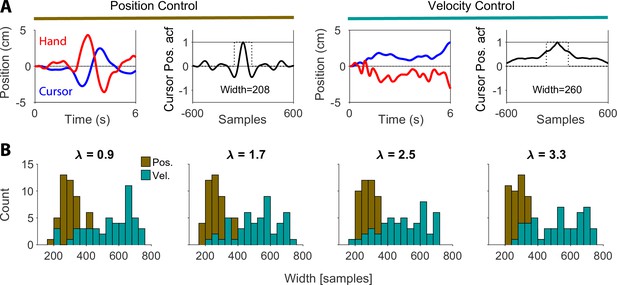
Autocorrelation analysis.
(A) Sample trials with autocorrelation functions (acf) of cursor position shown for position control (columns 1 and 2), and velocity control objectives (columns 3 and 4). The dotted rectangle in the acf plots shows the acf width (see text for definition). (B) Histograms of the acf width shown for Position (brown) and Velocity (cyan) control objectives. Each panel shows the results for a different value of as indicated.
Appendix 1—figure 3
Distribution of hand/cursor RMS ratio over trials, calculated for simulated trials under Position Control (brown) and Velocity Control (cyan), for different values.
Appendix 1—figure 4
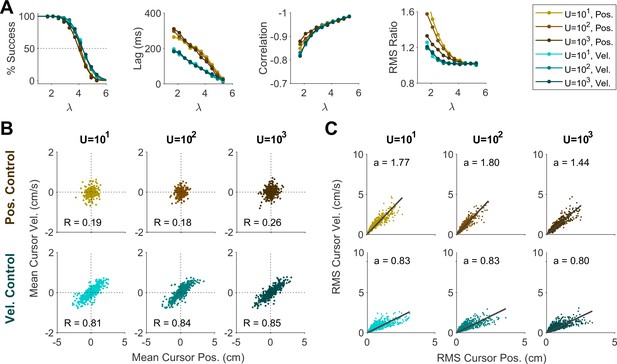
Effect of effort cost on control behavior represented by the (A) Aggregate performance measures, (B) Distribution of mean cursor movement, and (C) Distribution of RMS of cursor movement.
Appendix 1—figure 5
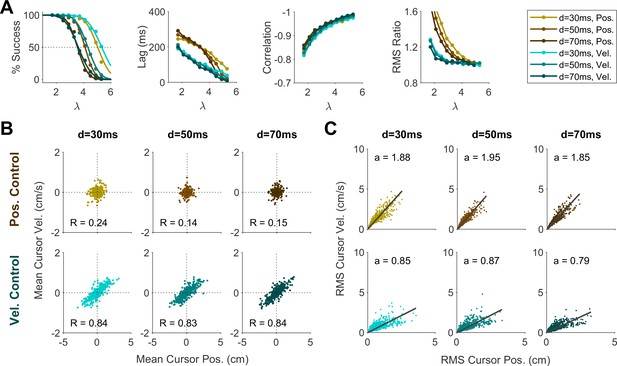
Effect of sensory delay on control behavior represented by the (A) Aggregate performance measures, (B) Distribution of mean cursor movement, and (C) Distribution of RMS of cursor movement.
Appendix 1—figure 6
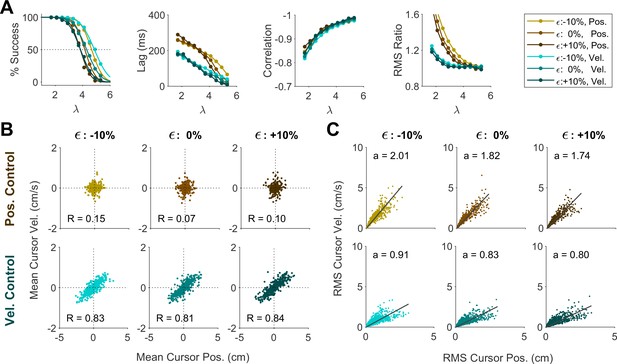
Effect of changing motor noise (10% reduction to 10% increase) on control behavior represented by the (A) Aggregate performance measures, (B) Distribution of mean cursor movement, and (C) Distribution of RMS of cursor movement.
Appendix 1—figure 7
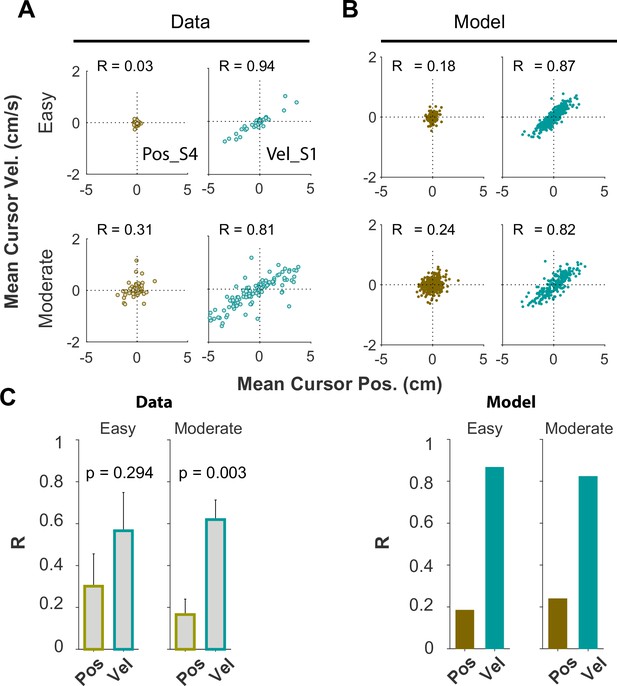
Joint distributions of cursor mean position and cursor mean velocity, separated into two difficulty levels: Easy ( ≤ 70% ), Moderate ().
(A) Experimental data and (B) Model data. (C) Correlation coefficient R between cursor mean position and mean velocity for different difficulty levels, plotted for data (left) and model (right). The error bars indicate standard error across subjects for each control objective group (n=6 per group).
Appendix 1—figure 8
Probability of each trial performed under Position Control for each individual and group (top: Position Control group; bottom: Velocity Control group).
Appendix 1—figure 9
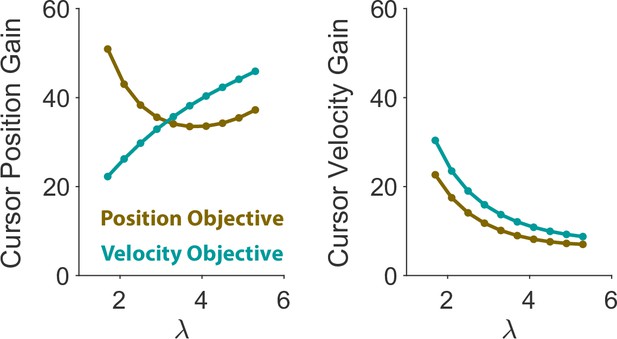
Optimal control gains corresponding to cursor position (left) and cursor velocity (right), obtained under Position Control (brown) and Velocity Control (cyan).
Appendix 1—figure 10
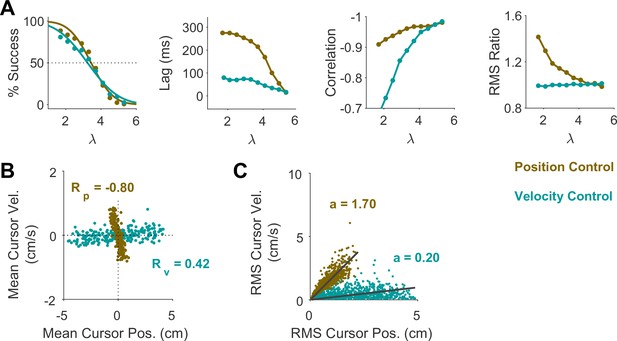
Model simulations of the CST task when introducing perturbations (random cursor jumps) at the start of each trial.
(A) Aggregate performance of success rate, hand/cursor lag, correlation and RMS ratio as a function of difficulty level, shown for each control objective (brown: Position Control; cyan: Velocity Control). (B) Joint distribution of cursor mean position and cursor mean velocity under different control objectives. (C) Distribution of cursor RMS position and RMS velocity under different control objectives.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Inferring control objectives in a virtual balancing task in humans and monkeys
eLife 12:RP88514.
https://doi.org/10.7554/eLife.88514.3
