Structural basis for the preservation of a subset of topologically associating domains in interphase chromosomes upon cohesin depletion
- Department of Chemistry, University of Texas at Austin, United States
- Department of Physics, University of Texas at Austin, United States
Figures
Figure 1
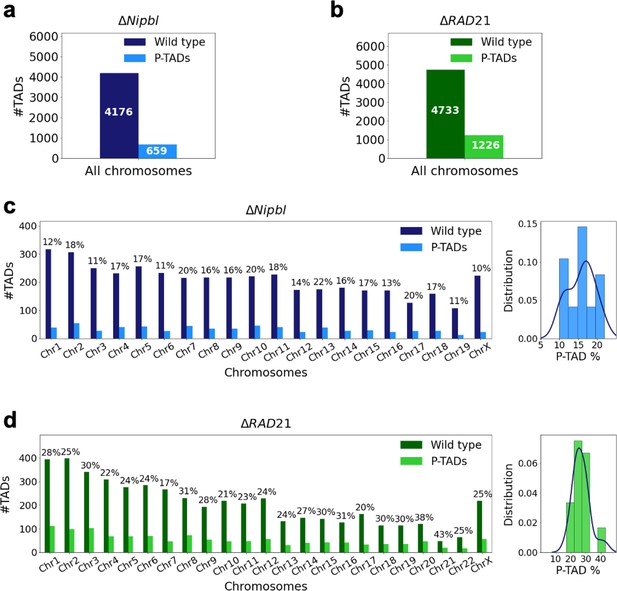
Fate of the topologically associating domains (TADs) in chromosomes upon cohesin deletion.
(a) The number of TADs in all the chromosomes, identified by the TopDom method (Shin et al. 2015), in the wild-type (WT) cells and the number of preserved TADs (P-TADs) after deleting cohesin loading factor (ΔNipbl) in mouse liver. (b) Same as (a) except the experimental data are analyzed for HCT-116 cell before (WT) and after RAD21 deletion. (c) The total number of TADs and the number of P-TADs for each chromosome calculated using the mouse liver Hi-C data. The number above each bar is the percentage of P-TADs in each chromosome. (d) Same as (c) except the results are for chromosomes from the HCT-116 cell line. The percentage of P-TADs is greater in the HCT-116 cell line than in mouse liver for almost all the chromosomes, a feature that is more prominent in the distribution of P-TAD proportions (right).
Figure 2
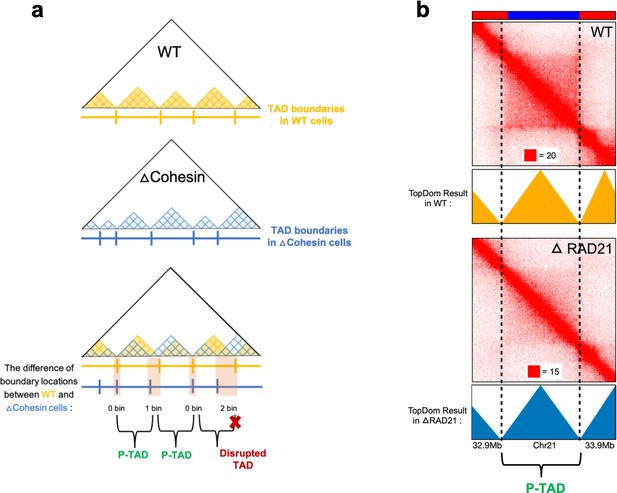
Identification of preserved topologically associating domains (P-TADs) from the contact map using the TopDom method.
(a) Schematic representation used to determine the P-TADs. Yellow (blue) triangles represent the TADs identified using the TopDom method in wild-type (WT) (cohesin-depleted) contact maps at 50 kb resolution. Small square within each triangle represents a single locus (50 kb size). The boundaries of a TAD detected in the WT contact map within ± one bin (50 kb) from a position of boundaries in cohesin-depleted cells are deemed to be a P-TAD. (b) P-TAD upon cohesin loss in HCT-116 cell. The bar plots above the contact maps show the epigenetic states. Red (blue) color represents the active (inactive) state. The TAD between gray dashed lines is preserved upon cohesin loss. The parameter (with red square) displayed at each left bottom indicates the color scale when plotting contact maps used in Juicebox (Robinson et al., 2018).
Figure 3
Chromosome copolymer model (CCM) simulations reveal characteristics of preserved topologically associating domains (P-TADs).
(a) The number of TADs in the simulated Chr10 and Chr13 chromosomes for . The number of P-TADs after CTCF loop depletion () is also shown. (b) The number of P-TAD with epigenetic switches (blue) and those identified by the peaks in the boundary probability (green). (c–e) Comparison between contact maps for the region of Chr13 with upper (lower) triangle with (). The black circles at the corner of the TADs are the CTCF loop anchors. The bars above the contact map are the epigenetic states with red (blue) representing A (B) loci. Arrows above the bar show the epigenetic switch. (c) After loop deletion, TAD structures disappear. (d) TAD whose boundaries are marked by epigenetic switches are preserved. (e) TAD lacking at least one epigenetic switch is disrupted after loop loss. (f–h) Comparison of the contact map and the mean spatial distance matrices for the 2.5 Mb genomic regions (25.7–28.2 Mbp, 73.3-75.8 Mbp, and 102–104.5 Mbp, respectively) with (upper) and without (lower) loop anchors. Bottom graph shows the boundary probability, with the high values indicating population averaged TAD boundary. Purple circles in the boundary probability graph represent the preferred boundaries. A subset of P-TADs boundaries matches epigenetic switches (blue lines). P-TADs with high boundary probability is shown by the green line. The magenta line describes P-TADs, which are not accounted for by epigenetic switch or physical boundary in 3D space but are found using the TopDom method.
Figure 4
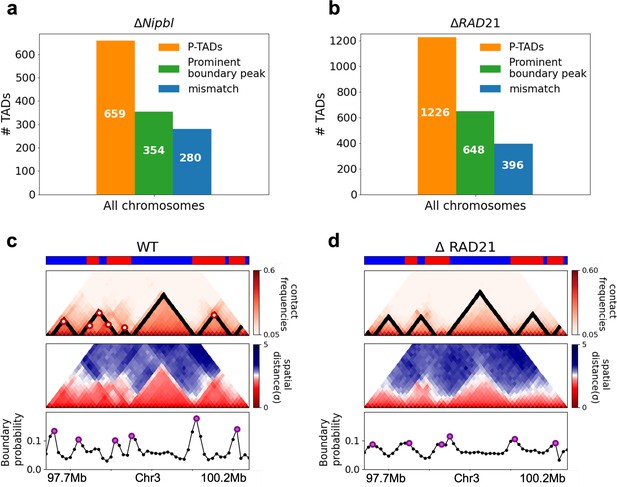
Classification of preserved topologically associating domains (P-TADs) from Hi-C maps from two cell lines and link between boundary probability peak and epigenetic switch.
(a) The number of P-TADs in all the chromosomes (orange bar taken from Figure 1a) that are accounted for by epigenetic switches (blue bar) as well as peaks in the boundary probability (green bar) after Nipbl loss in mouse liver. (b) Same as (a) except the analyses is done using experimental data are for HCT-116 cell after ΔRAD21. (c) Example of P-TAD in the WT 97.7–100.2 Mb region of Chr3 from HCT-116 cell line. The mean distance matrices calculated using the 3D structures are shown in the middle panel. The dark-red circles at the boundaries of the TADs in the contact maps are loop anchors detected using HiCCUPS (Durand et al., 2016). The peaks in the boundary probability (bottom panel) are shown by purple circles. Epigenetic switch coincides with peak in the boundary probability (compare top and bottom panels). Bottom plot shows the probability for each genomic position to be a single-cell domain boundary. (d) Same as (c) except the results correspond to the absence of RAD21. Although not as sharp, there is discernible peak in the boundary probability when there is an epigenetic switch after removal of RAD21.
Figure 5
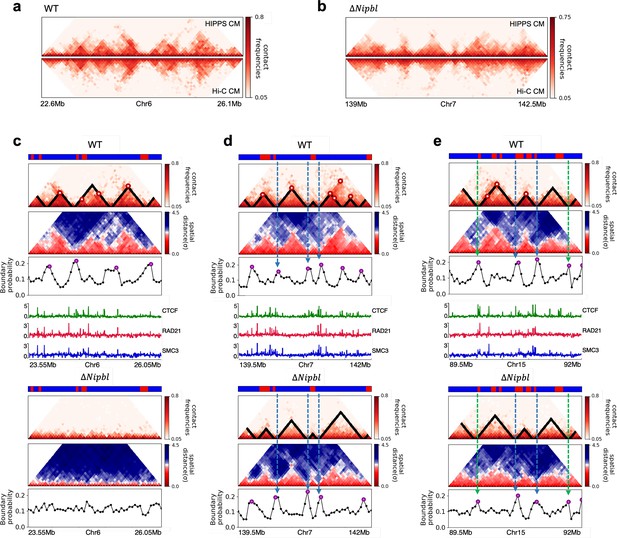
Fate of topologically associating domains (TADs) after ΔNipbl in mouse liver cells.
(a, b) Comparison between Hi-C (lower) and calculated contact maps (upper) using the 3D structures obtained from the Hi-C-polymer-physics-structures (HIPPS) method for the 3 Mb genomic regions (Chr6: 22.6–26.1 Mb in WT cells and Chr7: 139–142.5 Mb in Nipbl-depleted cells), respectively. The distance threshold for contact is adjusted to achieve the best agreement between HIPPS and experiments. Calculated contact maps are in very good agreement with Hi-C data for both WT and Nipbl-depleted cells. (c) Complete loss (Chr6: 23.55–26.05 Mb) of TADs in ΔNipbl. (d, e) Preserved topologically associating domains (P-TADs) (Chr7: 139.5–142 Mb and Chr15: 89.5–92 Mb). The plots below the scale on top, identifying the epigenetic states (Ernst and Kellis, 2012), compare 50-kb-resolution Hi-C contact maps for the genomic regions of interest with Nipbl (upper) and without Nipbl (lower). Mean spatial distance matrices, obtained from the Hi-C contact matrices using the HIPPS method (Shi and Thirumalai, 2021), are below the contact maps. The dark-red circles at the boundaries of the TADs in the contact maps are loop anchors detected using HiCCUPS (Rao et al., 2014). ChIP-seq tracks for CTCF, RAD21, and SMC3 in the WT cells (Schwarzer et al., 2017) illustrate the correspondence between the locations of the most detected loop anchors and the ChIP-seq signals. Bottom plots give the probabilities that each genomic position is at a single-cell domain boundary in the specified regions. Purple circles in the boundary probability graph represent the physical boundaries. A subset of physical boundaries in P-TADs coincides with epigenetic switches (blue lines), indicating that the probabilities of contact at these boundaries are small. P-TADs in (e), demarcated by green lines, have high peaks in the boundary probability in the absence of epigenetic switch.
Figure 6
Calculated 3D structures produce topologically associating domain (TAD)-like structures found in imaging experiments.
On the left panels are results for wild-type (WT) (ΔRAD21) for (Chr21: 34.6–37.1 Mb). For visualization purposes, we adopted the color scheme used in the imaging study (Bintu et al., 2018). (a) Hi-C contact maps with (left) and without RAD21 (Rao et al., 2017). (b) Mean distance matrices calculated from the Hi-C-polymer-physics-structures (HIPPS)-generated 3D structures. (c) Examples of calculated single-cell distance matrices with (left) and without (right) RAD21. Schematic of structures for the two cells under the two conditions are given below. (d) Distribution of the boundary strengths, describing the steepness in the changes in the spatial distance across the boundaries. The left is for the WT (ΔRAD21) cells. The blue (purple) histogram was calculated using HIPPS (experiments). (e) Position-dependent boundary probability for the WT (left) RAD21- deleted cells (right). The curve in blue (purple) is the calculated (measured) boundary probability for the WT cells. The orange (green) curve is from the calculations (experiments). The plots show that the location of prominent peaks in the calculated boundary probability is in excellent agreement with experiments for the WT cells (left panel). Without RAD21, high peaks are absent in both cases (right panel).
Figure 7
Certain topologically associating domains (TADs) enriched in enhancer–promoter/promoter–promoter (E–P/P–P) interactions at the boundary are preserved upon cohesin deletion.
(a) Comparison between 5 kb Micro-C contact maps in the region (Chr8: 72.24–72.57 Mb) for the wild-type (WT) (left panel) and cohesin-depleted (right panel) mouse embryonic stem cells (mESC) cells (Hsieh et al., 2022). Location of cohesin loops (green square) and E–P/P–P (blue circles) plotted in the WT contact maps are from experiments (Hsieh et al., 2022). Bars above the contact map show epigenetic states (red: active; blue: inactive) annotated based on ChromHMM results (Pintacuda et al., 2017). The cohesin-dependent (green dashed lines) and independent (blue dashed lines) TADs were detected in the WT cells using the TopDom method with default parameter (w = 5). P-TADs (blue dashed lines) are also found in cohesin-deleted cells. (b, c) Comparison between 20 kb Micro-C contact maps and mean distance maps spanning the regions, Chr19: 8.66–9.2 Mb and Chr12: 56.4–56.9 Mb, respectively, in the presence (upper) and absence (lower) of cohesin. Bottom graph, below the distance maps, shows the boundary probability calculated from 10,000 3D structures. P-TADs between gray dashed lines were detected using the TopDom method (w = 5). A P-TAD with high boundary peak, without epigenetic switches, is enriched due to E–P/P–P interactions at the boundaries.
Figure 8
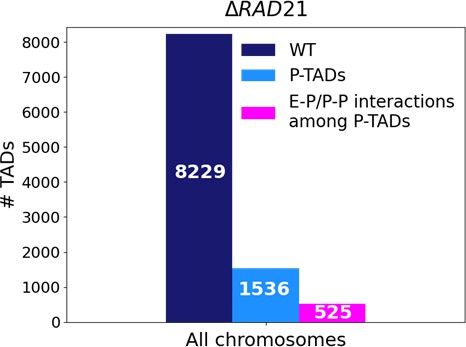
Statistics of the topologically associating domains (TADs) in chromosomes upon cohesin loss using Micro-C contact data.
The number of TADs in all the chromosomes in the wild-type (WT, dark blue bar), total number of preserved TADs (P-TADs, light blue bar) after deleting RAD21, and number of P-TADs whose boundaries coincide with enhancer–promoter/promoter–promoter (E–P/P–P) interactions (magenta bar) in mESC. About a third of the P-TADs are associated with E–P/P–P interactions.
Appendix 5—figure 1
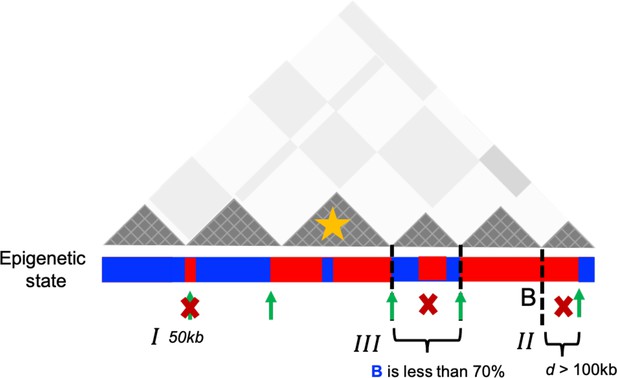
Schematic representation used to identify the preserved topologically associating domains (P-TADs) with epigenetic switches.
Dark gray triangles represent the P-TADs in contact map. Small square within each triangle represents a single locus (50 kb). Red (blue) color indicates the active (inactive) state in the bar below the contact map. A transition between A and B epigenetic states is referred to as epigenetic switch (green arrows). We examined whether each P-TAD has an epigenetic switch at the boundaries ±100 kb (II). If P-TADs have only one locus (50 kb) switch near their boundaries (I) or comprise <70% of sequences in identical epigenetic state (III), they are excluded. The TAD (yellow star) is a P-TAD with epigenetic switch at the TAD boundary.
Appendix 5—figure 2
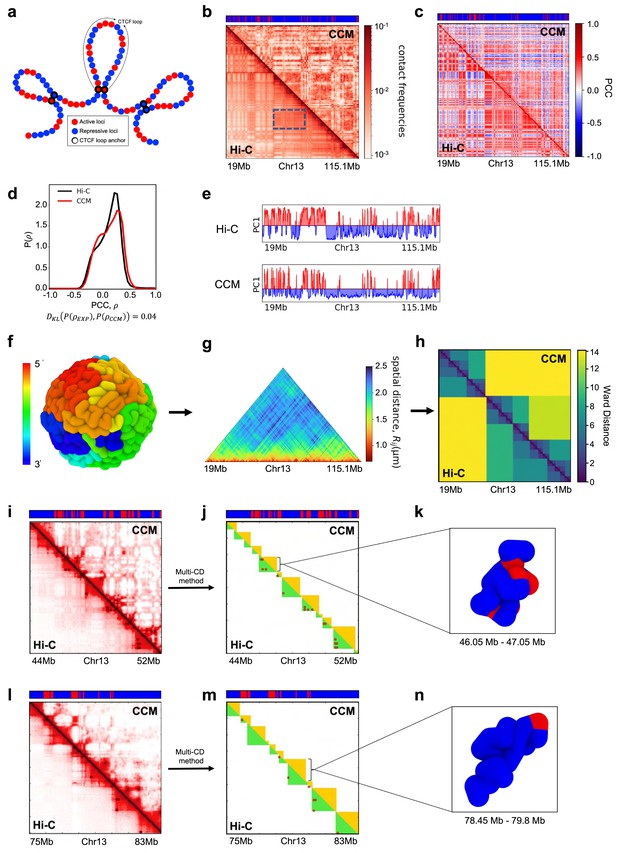
Chromosome copolymer model (CCM) simulations for chromosome 13 (Chr13) from the GM12878 cell line.
(a) In the CCM, red (blue) spheres represent active (repressive) loci. The black open circles are the CTCF loop anchor locations. (b) Comparison of the simulated (, top half) and Hi-C contact maps (bottom half). The bar above marks the epigenetic states with red (blue) representing active (repressive) loci. The values of the contact frequencies, converted to a scale, are shown on the right. (c) Comparison between the Pearson correlation maps consisting of for all loci pairs from simulations (top half) and experimental data (bottom half). The scale for the Pearson correlation coefficient (PCC) is on the right. (d) Distribution of the PCC, , for all pairs from simulations and experiment (1 is positive correlation, 0 is no correlation, and –1 corresponds to anti-correlation). The Kullback–Leibler, , value between CCM prediction and experiment is small. (e) First eigenvector values (PC1) from principal component analysis (PCA) using the correlation matrix for CCM. The compartments A and B are defined by positive (red) and negative (blue) values. (f) Snapshot of the folded Chr13. The color corresponds to genomic distance from one end point, ranging from red to green to blue. (g) Ensemble averaged distance map obtained from simulations. (h) Ward linkage matrix (WLM) comparison between simulations and the one computed using Hi-C data. The PCC between the two distance matrices is ∼0.83, indicating reasonable agreement between simulations and experiments. (i) Contact map for the 8 Mbp region ((44–52) Mb) with the upper (lower) triangle corresponding to simulations (experiments). (j) On the right is an Illustration of the TADs, identified using the Multi-CD method (Bak et al., 2021). The dark-red circles are the positions of the loop anchors detected in the Hi-C experiment, which are formed by two CTCF motifs. A subset of TADs is defined by the CTCF loops, whereas others are not associated with loops. These could arise from segregation between the chromatin states of the neighboring domains in certain experimental studies (Rowley et al., 2017; Beagan and Phillips-Cremins, 2020; Rao et al., 2017). The average sizes of the TADs detected using Multi-CD method from Hi-C and simulated contact maps are ∼750 kbs and ∼700 kbs, respectively. (k) Snapshot of the TAD, marked in (j). (m) Same as (j) except the TADs were calculated for the region ((75–83) Mb) in (l). (n) Snapshot of the TAD, marked in (n).
Appendix 5—figure 3
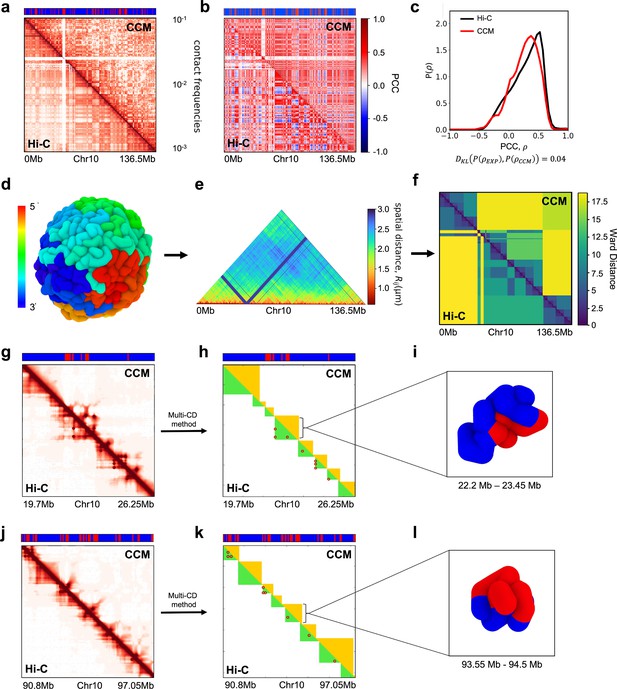
Organizational features of Chr10 from human cell line GM12878.
(a) Comparison between the simulated contact map (, top half) and Hi-C experiments (bottom half). The bar above the contact map shows the epigenetic states with red (blue) representing active (repressive) loci. (b) Experimental (lower triangle) and the simulated (upper triangle) Pearson correlation maps. (c) The distribution of the Pearson correlation coefficient (PCC), for each pair of from simulations and experiment. The value of the Kullback–Leibler (KL) divergence at the bottom is obtained by comparing the distributions obtained in the simulations and experiments. (d) A conformation of the folded Chr10 (N = 2712) obtained using the chromosome copolymer model (CCM) simulations. The colors correspond to genomic distance from the 5′ to 3′ end. (e) Ensemble averaged distance map calculated using the simulated structures. (f) Experimental (lower triangle) and simulated (upper triangle) Ward linkage matrices (WLMs). The PCC between the two WLMs is ∼0.75. The agreement between simulations and experiments is fair. (g) Hi-C map for the region (19.7–26.25) Mb, with the upper (lower) triangle corresponding to simulations (experiments). (h) Right is an illustration of the topologically associating domains (TADs). The dark-red circles are the positions of the loop anchors detected in the Hi-C experiment, formed by two CTCF motifs. (i) Snapshot of the TAD, marked by the black line in (h). (k) Same as (h) except the TADs were calculated for a region (90.8–97.05) Mb in (j). (l) Snapshot of the TAD, marked by the black line in (k). The diversity of TAD structures is apparent.
Appendix 5—figure 4
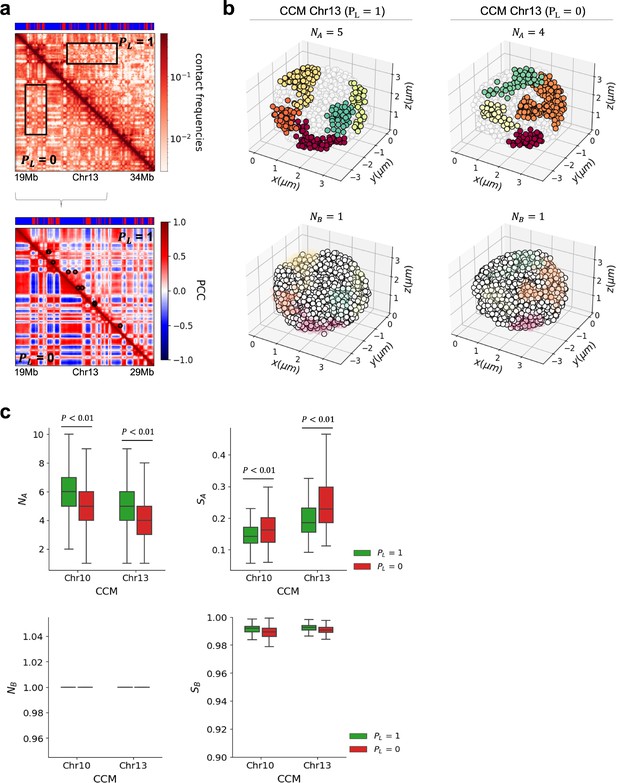
Clustering of A and B loci is stronger after loop (cohesin) loss.
(a) Comparison between simulated contact maps using chromosome copolymer model (CCM) (19–34 Mb, upper panel) and Pearson correlation maps (19–29 Mb, lower panel) for Chr13 (GM12878 cell line). Upper triangle (lower triangle) was calculated with (without) CTCF loops. The black circles in the upper triangle are the positions of the CTCF loop anchors detected in the Hi-C experiment (Rao et al., 2014). The bar on top marks the epigenetic states with red (blue) representing active (repressive) loci. Upon CTCF loop loss, the plaid patterns are more prominent, and finer details of the compartment organization emerge. (b) 3D snapshots of A and B clusters identified using the density-based spatial clustering of applications with noise (DBSCAN) algorithm, with (left panel) and (right panel) computed from simulations of Chr13 with and without loops, respectively. Five A clusters (upper panel; red, orange, yellow, dark-green, light-green) and one B cluster (lower panel; white) were detected in this 3D structure with . Four A clusters and one B cluster were detected for . The size of a locus σ50K ≈ 243 nm (Shi and Thirumalai, 2021). (c) Box plot of the number (left) and average size (right) of A (B) clusters determined using 10,000 individual 3D structures for and for simulated Chr10 and Chr13. The size of the A (B) cluster, (), is defined as (the number of A (B) loci within the cluster)/(the total number of A (B) loci within the chromosome). Boxes depict median and quartiles. The black line with caps describes the range of values in the number and size. Loop loss creates a smaller number (enhancement in compartment strength) of A-type clusters whose sizes are larger (upper). Two-sided Mann–Whitney U test was performed for the statistical analysis. There is no change in the number and size of B clusters after loop deletion (lower).
Appendix 5—figure 5
Clustering of A and B loci is stronger after loop (cohesin) loss.
(a, b) Same as Appendix 5—figure 4c except the results were determined using 10,000 3D structures generated with the Hi-C-polymer-physics-structures (HIPPS) method from the experimental Chr11 and Chr19 contact maps (Chr6 and Chr15 contact maps) from mouse liver for the wild-type (WT) and ∆Nipbl (Schwarzer et al., 2017) (HCT-116 in WT and ∆RAD21 cells [Rao et al., 2017]), respectively. The number of A clusters decreases by 18 and 27% after Nipbl loss in Chr11 and Chr19, respectively. (c, d) Pearson correlation matrix derived from 3D structures for Chr11 and Chr19 of mouse liver, respectively. Two loci, separated by a distance smaller than 1.75σ, are in contact (σ is the mean distance between and loci for WT and ∆Nipbl, respectively). The black circles in the upper triangle are loop anchors detected in Hi-C map (Schwarzer et al., 2017) using HiCCUPS (Rao et al., 2014). (e) The percentage of decrease in the number of A (B) clusters after CTCF loop or cohesin loss for some chromosomes in simulations and experiments as a function of the percentage of A (B) loci within the chromosome. When the proportion of B loci is much larger than A loci, there is no change in B clusters despite loop or cohesin deletion (upper panel).
Appendix 5—figure 6
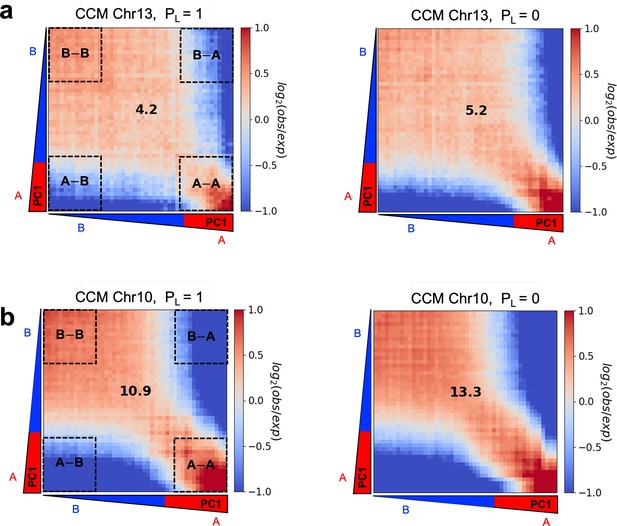
Enhancement of compartmentalization upon CTCF loop loss.
Compartmentalization saddle plots are shown for (a) Chr13 and (b) Chr10 with (left) and (right). Observed/expected matrix bins are arranged based on PC1, obtained from the contact maps without loops. Numbers at the center of the maps represent compartment strengths defined as the ratio of ((AA) and (BB) interactions) to ((AB) and (BA) interactions) using the mean values from the corners. The increase in the compartment score (4.2–5.2 for Chr13 and 10.9–13.3 for Chr10) shows that the compartment features are accentuated in (loop deletion) compared to , which accords well with the conclusions in the main text that uses a different method.
Appendix 5—figure 7
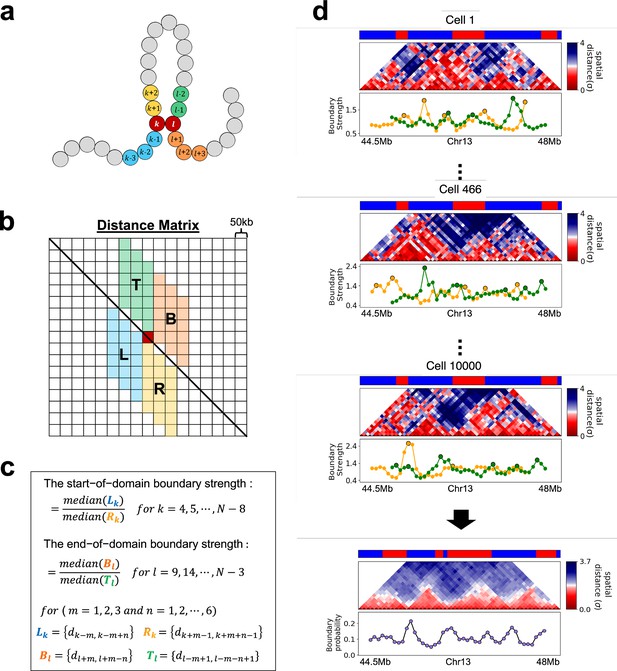
Calculation of boundary strength and boundary probability from the distance matrix at 50 kb resolution.
(a) A schematic describing the chromosome model. (b) Each small square of size (=50 kb) represents distance, between two loci and . The red square is used to illustrate the idea. (c) Definition of the start and end of domain boundary strengths in the N × N distance matrix. The distance between the loci is represented as arcs in various colors. (d) The distance maps in 10,000 cells are calculated using the 3D structures using the HIPPS method (Shi and Thirumalai, 2021) with Hi-C contact map from Schwarzer et al., 2017 as input. Local maxima above a defined threshold at the start/end of domain boundary strengths (yellow and green lines, respectively) are defined as domain boundaries in the WT Chr13. The start/end boundary probabilities for each locus are calculated as the proportion of cells in which the corresponding locus is a boundary location. The average of the start and end boundary probabilities covers 10,000 cells and is defined as the boundary probability for a given locus.
Appendix 5—figure 8
ChromHMM chromatin state annotation in HCT-116 cells.
Appendix 5—figure 9
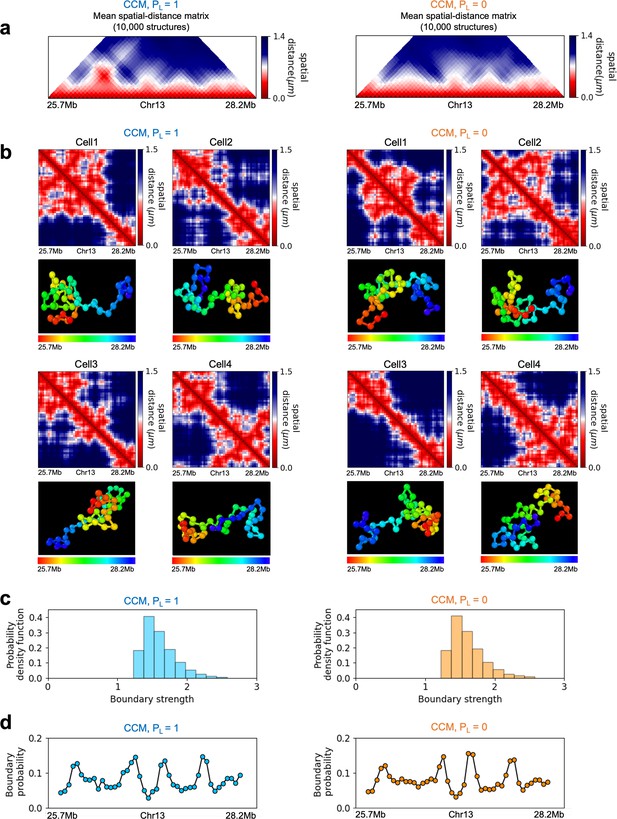
Single-cell topologically associating domain (TAD)-like structures are exhibited in both and .
(a) Mean spatial distance matrix for the genomic region (25.7–28.2 Mbps) in chromosome copolymer model (CCM) Chr13 without (left) and with (right) CTCF loops. (b) Examples of single-cell spatial distance matrices calculated from the simulated 3D structures. TAD-like structures vary from cell to cell in both (left) and (right). Schematic of structures for the four cells under the two conditions is given below. (c) Distribution of the boundary strengths before (left) and after (right) CTCF loop loss, describing the steepness in the changes in the spatial distance across the boundaries. (d) The probability for each locus to be a single-cell domain boundary in cells for (left) and (right).
Appendix 5—figure 10
Same as Appendix 5—figure 9 except the results are for the genomic region (123.5–126 Mb) in Chr4 of mouse liver (Schwarzer et al., 2017) with (left) and without (right) cohesin loading factor Nipbl.
Hi-C-polymer-physics-structures (HIPPS)-generated single-cell spatial distance matrices using Hi-C contact maps as inputs.
Appendix 5—figure 11
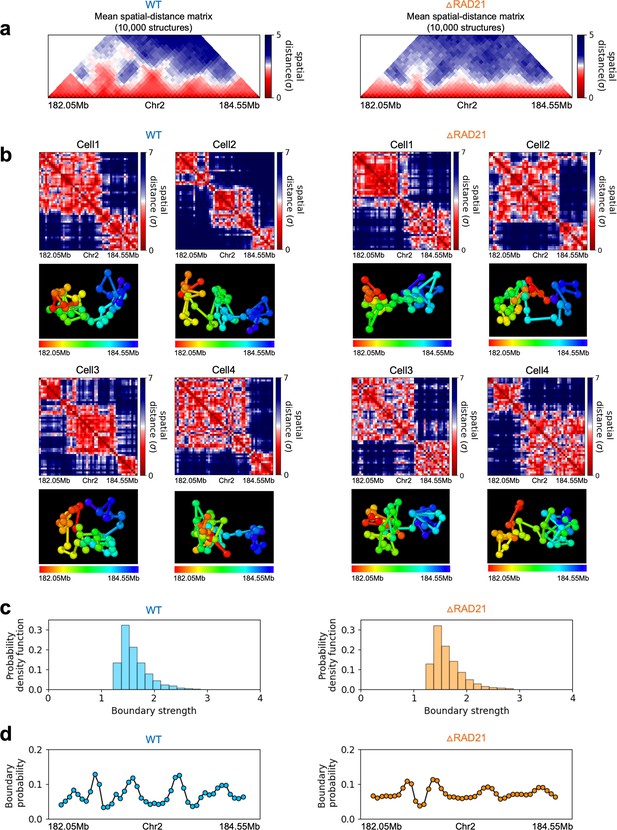
Same as Appendix 5—figure 9 except the results are for the genomic region (182.05–184.55 Mb) in Chr2 of HCT-116 (Rao et al., 2017) with (left) and without (right) a core component of the cohesin complex, RAD21.
Single-cell 3D structures were calculated from Hi-C contact maps using Hi-C-polymer-physics-structures (HIPPS).
Appendix 5—figure 12
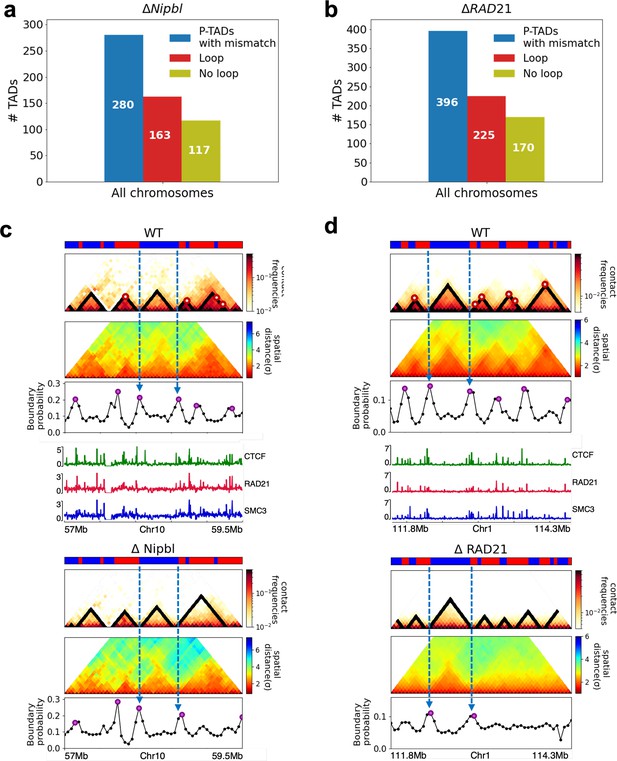
Epigenetic states contribute to the formation of domain boundaries.
Preserved topologically associating domain (P-TAD) does not always have corner dots at their boundaries in the wild-type (WT) cells. (a) The number of P-TADs (after ΔNipbl) whose boundaries coincide with both epigenetic switches and corner dots (CTCF loop anchors) (red color) and only epigenetic switches (olive color) in the WT chromosomes from mouse liver. (b) Same as (a) except the results are obtained using experimental data from HCT-116 cell. (c) Chr10: 57–59.5 Mb in mouse liver and (d) Chr1: 111.8–114.3 Mb in HCT-116 cells, respectively. Comparison between 50-kb-resolution contact maps for the 2.5 Mb region with (upper) and without (lower) Nipbl (RAD21). The panels below show the mean distance maps obtained from the 3D structures. ChIP-seq tracks for CTCF, RAD21, and SMC1 in WT cells (Schwarzer et al., 2017; Rao et al., 2014) illustrate the correspondence between the locations of the detected loop anchors and the ChIP-seq signals. Comparison of the contact maps and boundary probabilities in (c) and (d) shows that the P-TAD boundaries (blue dotted lines) correspond well with epigenetic switch (blue line) even without corner dots in WT cells. Purple circles in the boundary probability graph represent the preferred boundaries.
Appendix 5—figure 13
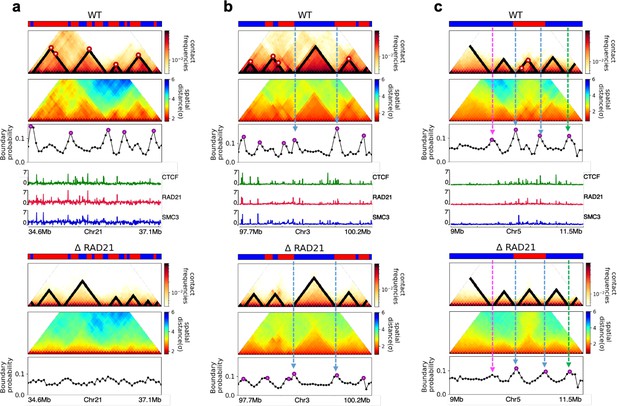
Fate of topologically associating domain (TAD) structures after loss of RAD21 in HCT-116 cells.
(a) Complete loss (Chr21: 34.6–37.1 Mb). (b, c) Preserved (Chr3: 97.7–100.2 Mb and Chr5: 9–11.5 Mb). 50-kb-resolution contact maps for the 2.5 Mb genomic regions of interest with (upper) and without (lower) RAD21 are shown in the middle panels. The dark-red circles at the boundaries of the TADs in the contact maps are loop anchors detected using HiCCUPS (Durand et al., 2016). The mean distance maps calculated using the 3D structures with and without RAD21 are compared in the top and bottom panels. ChIP-seq tracks for CTCF, RAD21, and SMC1 in WT cells (Rao et al., 2014) illustrate the correspondence between the locations of the detected loop anchors and the ChIP-seq signals. Bottom plots are the probability for each genomic position to be a single-cell domain boundary in the regions for cells. Purple circles in the boundary probability graph represent the preferred boundaries. Some P-TAD boundaries match epigenetic switch (blue lines). P-TADs have only high peaks in boundary probability (green line) without evidence for epigenetic switch. The magenta line shows discordance between TopDom and boundary probability.
Appendix 5—figure 14
Examples of discordance between TopDom and boundary probability predictions in mouse liver (Schwarzer et al., 2017).
In all cases, the plots show contact maps with TopDom results, mean spatial distance matrix, and boundary probability for the 2.5 Mb region (a) (Chr1: 172–174.5 Mb), (b) (Chr4: 137.5–140 Mb), and (c) (Chr10: 8.7–11.2 Mb) with (top) and without (bottom) Nipbl. Purple circles in the boundary probability indicate the prominent physical boundary in 3D structures. The magenta lines represent discordance between TopDom and boundary probability.
Tables
Table 1
Parameters for bonding potentials.
| 2.497 | 5.199 | 24.97 | 3.916 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Structural basis for the preservation of a subset of topologically associating domains in interphase chromosomes upon cohesin depletion
eLife 12:RP88564.
https://doi.org/10.7554/eLife.88564.3
