MotorNet, a Python toolbox for controlling differentiable biomechanical effectors with artificial neural networks
- Western Institute for Neuroscience, University of Western Ontario, Canada
- Department of Psychology, University of Western Ontario, Canada
- Department of Physiology & Pharmacology, Schulich School of Medicine & Dentistry, University of Western Ontario, Canada
- Robarts Research Institute, University of Western Ontario, Canada
Figures
Figure 1
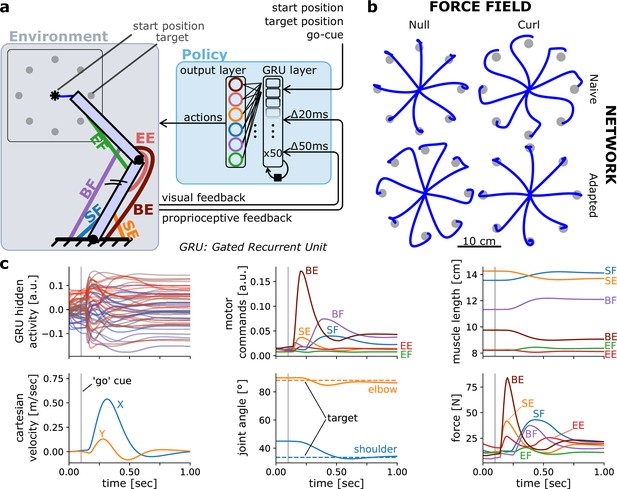
Controlling an arm-like effector in a centre-out reaching task with a curl field.
(a) Schematic of the environment (containing the effector) and policy. (b) Endpoint trajectories of centre-out reaching movements in a null and curl field, for a policy recurrent neural network (RNN) that is untrained (naive) and then trained to reach in that curl field. The effector was as defined in Kistemaker et al., 2010. (c) Different variables over time during a rightward reaching movement.
Figure 2
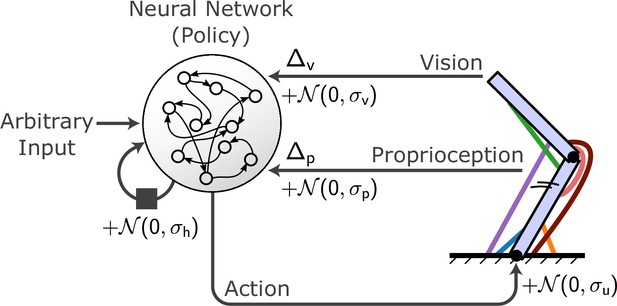
Conceptual organization of a MotorNet model.
A policy artificial neural network (ANN) receives arbitrary input as well as recurrent connections from itself and sends action signals to an effector embedded in an environment, which in turn sends sensory feedback information. Typically, this feedback will be visual and proprioceptive, and can contain feedback-specific time delays Δp and Δv. Gaussian noise can be added to the recurrent connection, action signal, and proprioceptive and visual feedback, with specific standard deviation σh, σu, σp, and σv.
Figure 3
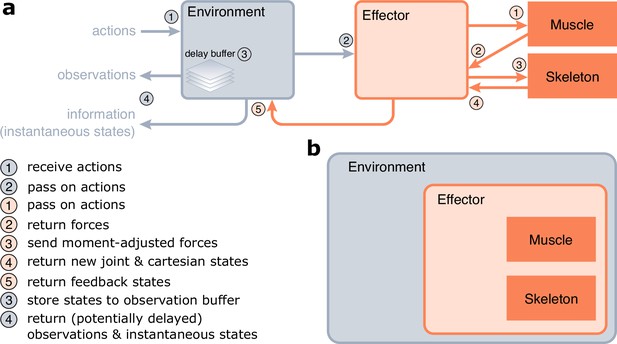
Implementation of MotorNet.
(a) Information flow of a MotorNet model during runtime. (b) Declarative structure of a MotorNet object. Each object instance is held in memory as an attribute of another according to this hierarchical representation, except for the Muscle, and Skeleton instances.
Figure 4
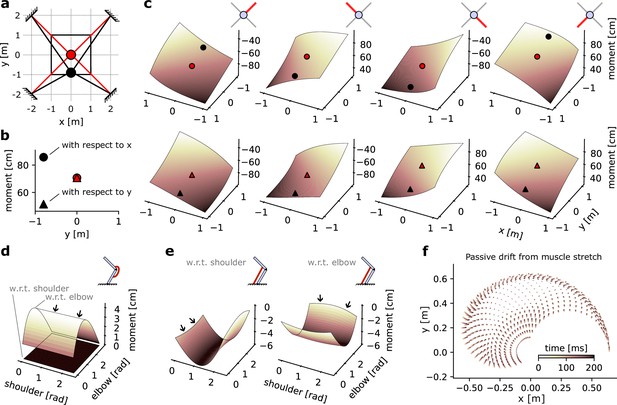
Geometrical properties of an Effector object.
(a) Schematic of a point-mass in two positional configurations within a square workspace. The point-mass Skeleton was linked to four muscles in a ‘X’ configuration. (b) Moment arm values for the lower left muscle for each of the positional configurations represented in (a), with respect to x and y. (c) Complete moment arm function over the position space for each muscle (columns) and with respect to each degrees of freedom (DoF). The upper and lower rows indicate the moment arm with respect to the x and y positions, respectively. (d) Moment arms of a mono-articular extensor muscle on an arm26. (e) Moment arms of a bi-articular flexor muscle on an arm26. (f) Passive drift in endpoint position of an arm26 similar to Figure 1c due to passive force developed by overstretch Hill-type muscles.
Figure 5
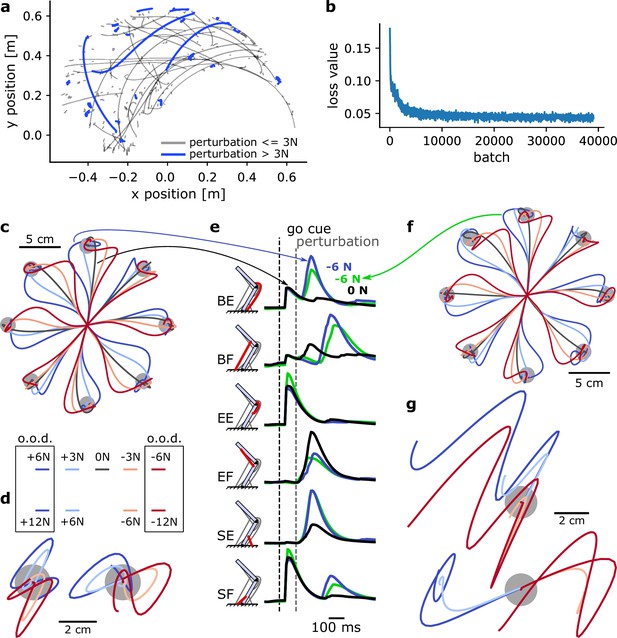
A MotorNet model can learn a control policy that generalizes to out-of-distribution perturbations.
(a) Example endpoint trajectories produced by a network after training. (b) Loss function over training iterations, with a batch size of 1024. (c) Trajectories in a centre-out reaching task with mechanical perturbations applied at the arm’s endpoint 120 ms after the ‘go’ cue. The perturbations were orthogonal to the reaching axis passing from the starting position to the target. o.o.d.: out-of-distribution. (d) Same as (c) for a postural control task. In this task, the network was not provided with a target and therefore only had to remain in the starting position against the perturbations. Mechanical perturbations were in the vertical (left) or horizontal (right) axis. (e) Muscle activation over time for two trajectories in (c) (black and blue lines) and a trajectory in (g) (green line). BE: bi-articular extensor; BF: bi-articular flexor; EE: elbow extensor; EF: elbow flexor; SE: shoulder extensor; SF: shoulder flexor. (f) Reaching task as in (c) for a network never exposed to mechanical perturbations during training. (g) Postural task as in (d) for the same network as in (f). Perturbations were in the vertical (top) or horizontal (bottom) axis.
Figure 6
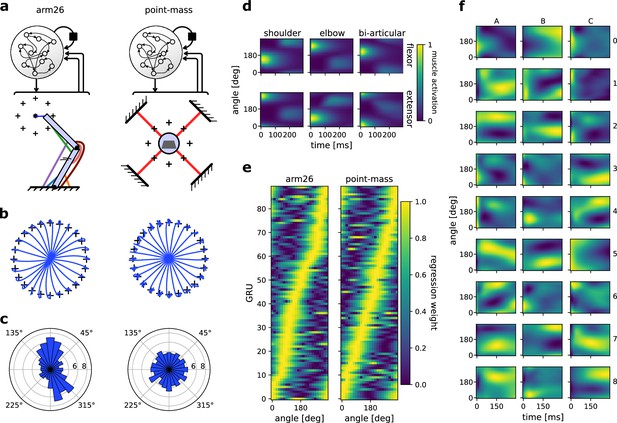
The distribution of preferential movement direction (PMD) tuning is sensitive to the geometry of the effector.
(a) Schematic of the two models compared. The recurrent neural networks (RNNs) and their architecture were identical, but the effector differed, with one RNN controlling a two-joint arm26 (left) and the other controlling a point-mass (right). (b) Centre-out reaching trajectories to 24 targets for the arm26 (left) and point-mass (right) model. (c) Distribution of PMDs for the arm26 (left) and point-mass (right) model. The PMDs were determined by regression of each gated recurrent unit’s (GRU) hidden activity averaged over time against reach angle (see Methods for details). (d) Normalized muscle activations across reaching angles and for the 300 ms following the ‘go’ cue for the arm26 model. (e) Normalized β coefficients of the regression models used for (c). The GRUs were ordered according to the angle of their maximum β value. Note that the ‘ridge’ of maximum β yields roughly a straight line for the point-mass model, while it yields a crooked line for the arm26, indicative of a representation bias. (f) Hidden activity over time and across reaching angles for a random sample of GRUs in the arm26 model.
Figure 7
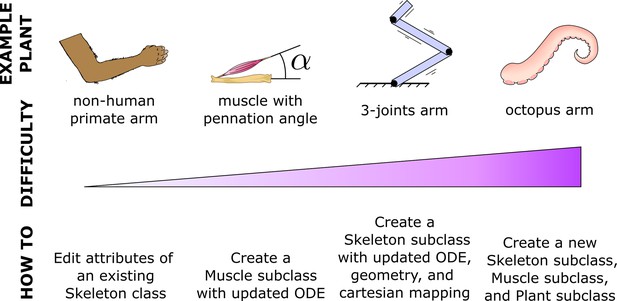
MotorNet is expandable.
MotorNet allows for new features to be implemented through subclassing.
Figure 8
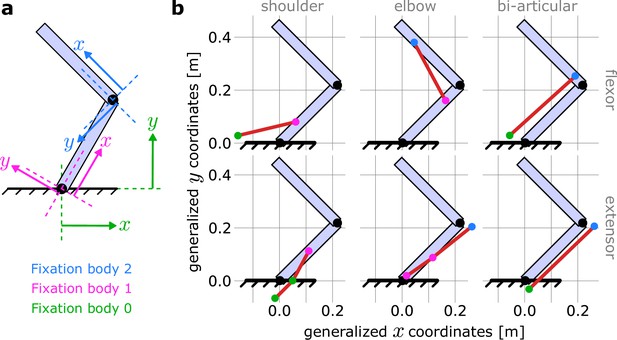
Coordinate frames for declaring muscle paths in MotorNet.
(a) MotorNet handle muscle paths using coordinate frames relative to the bone on which a fixation point is. The world space is indexed as the fixation body ‘0’ and its coordinate frame is the general coordinate system. (b) Schematic illustration of the muscle paths used for the arm26 model with no moment arm approximation described in section ‘Biomechanical properties of the effector’ and Table 5, for a shoulder and elbow angle of 45° and 90°, respectively.
Tables
Table 1
Overview of Python base classes and their respective pre-built subclasses in MotorNet.
GRU: gated recurrent unit.
| Subclass | Description | |
|---|---|---|
| Skeleton | PointMass | A skeleton with one bone of null length evolving in a plane. |
| TwoJointArm | A planar, two-segment skeleton with one hinge joint between the segments and the remaining end of one segment anchored to the world space. | |
| Muscle | ReluMuscle | An actuator that produces forces according to a linear piece-wise function of activation. The lower bound of force production is 0. |
| RigidTendonHillMuscle | A Hill-type muscle according to the formalization in Kistemaker et al., 2010, adjusted for rigid-tendon dynamics. | |
| RidigTendonHillMuscleThelen | A Hill-type muscle according to the formalization in Thelen, 2003, adjusted for rigid-tendon dynamics. | |
| CompliantTendonHillMuscle | A Hill-type muscle according to the formalization in Kistemaker et al., 2010. | |
| Effector | ReluPointMass24 | A planar (2D) PointMass with four ReluMuscle actuators. |
| RigidTendonArm26 | A TwoJointArm with six RigidTendonHillMuscle actuators. | |
| CompliantTendonArm26 | A TwoJointArm with six CompliantTendonArm26 actuators. | |
| Environment | CentreOutReach | A centre-out reaching task. |
| DelayedReach | A reaching task where movement initiation is signified by the appearance of a ‘go’ cue. | |
| DelayedMultiReach | A reaching task where movement initiation is signified by the appearance of a ‘go’ cue, and several targets appear in sequence for each trial. | |
| Policy | PolicyGRU | An RNN network comprising a user-defined number of layers containing a user-defined number of GRUs. |
Table 2
Skeleton parameters for the arm26 model, taken from Nijhof and Kouwenhoven, 2000.
The skeleton was actuated by six rigid-tendon versions of Hill-type muscle actuators: a shoulder flexor, a shoulder extensor, an elbow flexor, an elbow extensor, a bi-articular flexor, and a bi-articular extensor. Their parameter values are defined in Table 3.
| Parameter | Upper arm | Forearm |
|---|---|---|
| Mass (kg) | 1.82 | 1.43 |
| Centre of gravity (m) | 0.135 | 0.165 |
| Inertia (kg·m2) | 0.051 | 0.057 |
| Length (m) | 0.309 | 0.333 |
Table 3
Parameters for the Hill-type muscle actuators used in the arm26, taken from Kistemaker et al., 2010.
| Muscle | Maximum isometric force (N) | Tendon length (m) | Optimal muscle length (m) |
|---|---|---|---|
| Shoulder flexor | 838 | 0.039 | 0.134 |
| Shoulder extensor | 1207 | 0.066 | 0.140 |
| Elbow flexor | 1422 | 0.0172 | 0.092 |
| Elbow extensor | 1549 | 0.187 | 0.093 |
| Bi-articular flexor | 414 | 0.204 | 0.137 |
| Bi-articular extensor | 603 | 0.217 | 0.127 |
Table 4
Parameters used to compute moment arms in the arm26 models with moment arm approximation, taken from Kistemaker et al., 2010.
| Muscle | ||||
|---|---|---|---|---|
| Shoulder flexor | 0.151 | 0 | −0.03 | 0 |
| Shoulder extensor | 0.2322 | 0 | 0.03 | 0 |
| Elbow flexor | 0.2859 | −0.014 | 0 | −4.0e−3 |
| Elbow extensor | 0.2355 | 0.025 | 0 | −2.2e−3 |
| Bi-articular flexor | 0.3329 | −0.016 | −0.3 | −5.7e−3 |
| Bi-articular extensor | 0.2989 | 0.03 | 0.03 | −3.2e−3 |
Table 5
Muscle paths for the arm26 model with no moment arm approximation.
| Muscle | Fixation point | Fixation body | First coordinate (m) | Second coordinate (m) |
|---|---|---|---|---|
| SF | 1 | 0 (world) | −0.15 | 0.03 |
| 2 | 1 (upper arm) | 0.094 | 0.017 | |
| SE | 1 | 0 (world) | −0.013 | −0.07 |
| 2 | 0 (world) | 0.05 | 0 | |
| 3 | 1 (upper arm) | 0.153 | 0 | |
| EF | 1 | 1 (upper arm) | 0.23 | 0.001 |
| 2 | 2 (forearm) | 0.231 | 0.01 | |
| EE | 1 | 1 (upper arm) | 0.03 | 0 |
| 2 | 1 (upper arm) | 0.138 | −0.019 | |
| 3 | 2 (forearm) | −0.04 | −0.017 | |
| BF | 1 | 0 (world) | −0.052 | 0.033 |
| 2 | 2 (forearm) | 0.044 | 0.001 | |
| BE | 1 | 0 (world) | 0.02 | −0.028 |
| 2 | 2 (forearm) | −0.04 | −0.017 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
MotorNet, a Python toolbox for controlling differentiable biomechanical effectors with artificial neural networks
eLife 12:RP88591.
https://doi.org/10.7554/eLife.88591.4
