Figures and data in Structural constraints on the emergence of oscillations in multi-population neural networks

Figures
Tables
Additional files

5 figures, 11 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

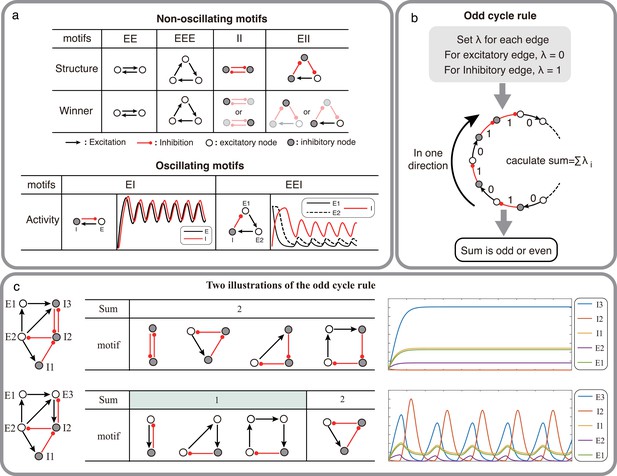
Structural condition for oscillations: odd inhibitory cycle rule and its illustrations.

(a) Examples of oscillating motifs and non-oscillating motifs in Wilson-Cowan model. Motifs that cannot oscillate show features of Winner-take-all: the winner will inhibit other nodes with a high activity level. Inversely, the oscillatory ones all show features of winner-less competition, which may contribute to oscillation. (b) The odd inhibitory cycle rule for oscillation prediction with the sign condition of a network. (c) Illustrations of oscillation in complex networks. Based on the odd inhibitory cycle rule, Network I can’t oscillate, while Network II could oscillate by calculating the sums of their motifs. The red or black arrows indicate inhibition or excitation, respectively. Hollow nodes and solid nodes represent excitatory and inhibitory nodes, respectively.

Figure 2

Download asset Open asset

The intuitive explanations of Theorem 1 and 2.

(a) A visual representation of why directed cycles are important in network oscillation. By rearranging all nodes, any network without directed cycles can be seen as a feed-forward network which will make the system reach a stable fixed point. (b) An intuitive explanation of the odd inhibitory cycle rule by showing the activities of two 6-node-loops. Odd inhibitory connections (bottom) can help the system oscillate, while even inhibitory connections has the opposite effect.

Figure 3 with 3 supplements

Download asset Open asset

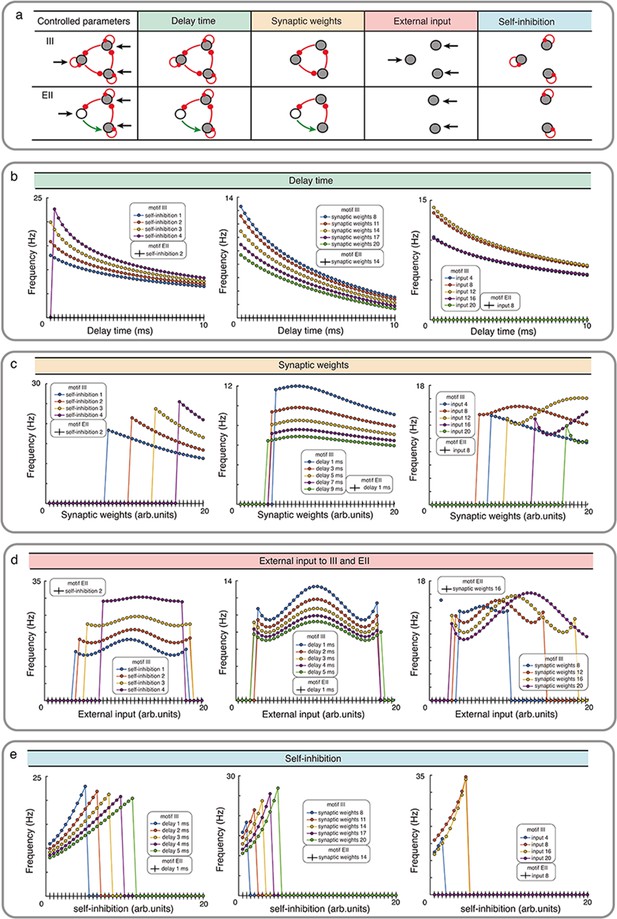
Influence of network properties on the oscillation frequency in motifs III and EII with Wilson-Cowan model.

(a) The changed network parameters are shown in the table. Red (green) connections are inhibitory (excitatory) and black arrows are the external inputs. (**b-e**) We systematically varied the synaptic delay time b, synaptic weights c, external input d, and self-connection e. These parameters were varied simultaneously for all the synapses i.e. in each simulation all synapses were homogeneous. Green, orange, red and turquoise respectively show the effect of synaptic delay, synaptic strength, external input and self-inhibition. See the Figure 3—figure supplement 1 and Figure 3—figure supplement 3 for more detailed results about III and EI network motifs.

Figure 3—figure supplement 1

Download asset Open asset

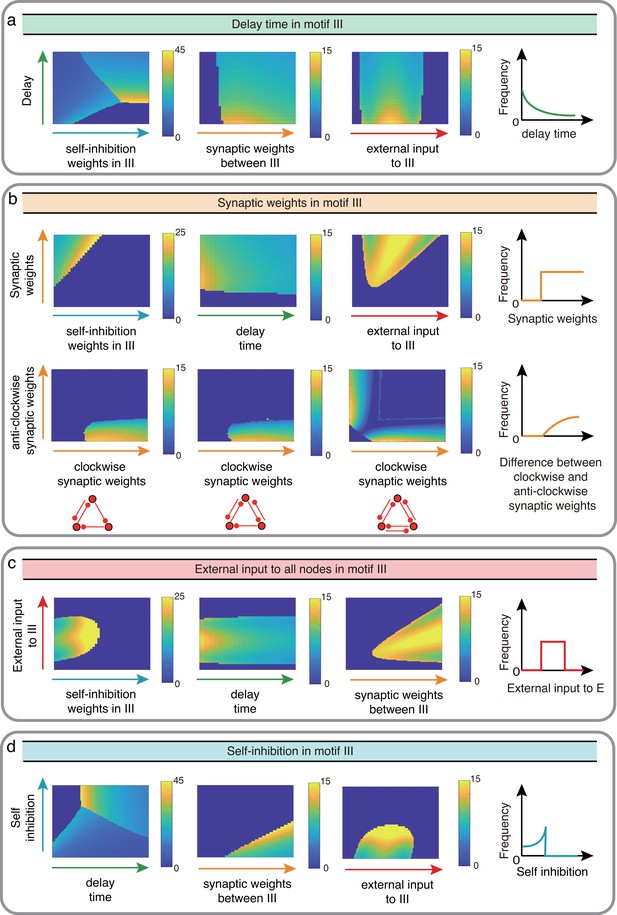
Influence of III network properties on the oscillation frequency in Wilson-Cowan model.

The controlled properties in motif III, including delay time a, synaptic weights b, external input c, and self-connection d, are denoted successively by green, orange, red and blue. We controlled two factors once at a time to observe the reaction of oscillation frequency with sketch maps on the right as conclusions.

Figure 3—figure supplement 2

Download asset Open asset

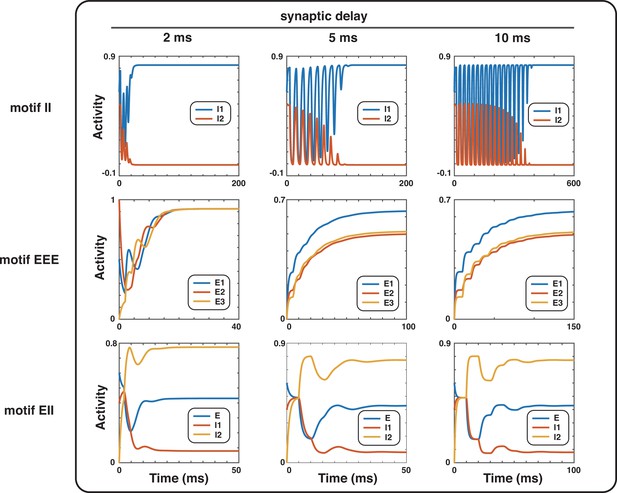
Effect of synaptic delays on motifs with even inhibition in the Wilson-Cowan model.

The synaptic delays are varied from 2ms to 10ms in motifs II, EEE, and EII, with corresponding external inputs to nodes being [4, 4], [2.2, 2, 1.8], and [3, 3, 3].

Figure 3—figure supplement 3

Download asset Open asset

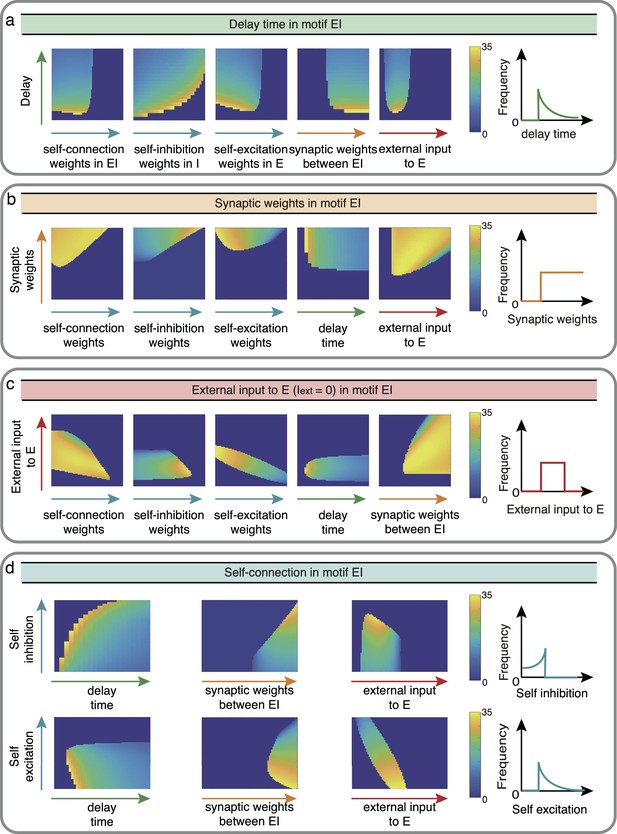
Influence of EI network properties on the oscillation frequency in Wilson-Cowan model.

The controlled properties in motif EI, including delay time a, synaptic weights b, external input c, and self-connection d, are denoted successively by green, orange, red and blue. We controlled two factors once at a time to observe the reaction of oscillation frequency with sketch maps on the right as conclusions.

Figure 4 with 6 supplements

Download asset Open asset

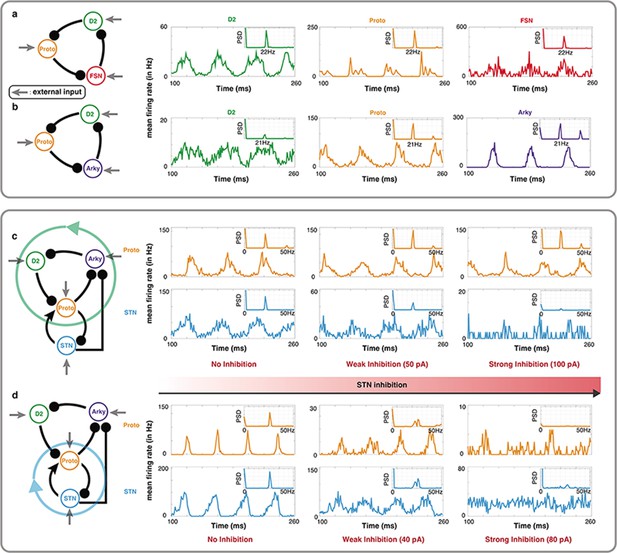
Schematic of CBG network model with potential oscillators and the interaction between two oscillators in Wilson-Cowan model.

(a) CBG structure with red lines denoting inhibition and green lines denoting excitation, along with five potential oscillators based on the odd inhibitory cycle rule. (b) Oscillation in all BG motifs from 2 nodes to 6 nodes based on the odd inhibitory cycle rule. Each grid represents a separate motif. We use different colors to mark potential oscillators in each motif in BG, and each color means an oscillator from panel a. For more details, see Figure 4—figure supplements 1–6. (c) The reaction of oscillation frequency to different external inputs to D2 and STN in a BG subnetwork. External inputs to Proto and Arky are 1 and 3, respectively. (d) Same thing as c but ruining the connection from D2 to Proto. (e) Same thing as c but destroying the connections from STN and increasing the input to Proto from 1 to 4.

Figure 4—figure supplement 1

Download asset Open asset

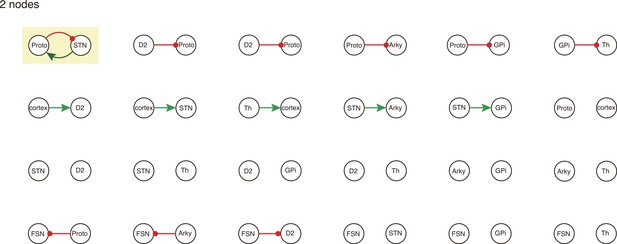
All 2-node-motifs in CBG network.

Potential oscillating motifs behind these subnetworks are marked with different colors. Yellow: motif Proto-STN; Orange: motif STN-GPi-Th-cortex; Blue: motif Proto-Arky-D2; Green: motif Proto-FSN-D2; Purple: motif Proto-GPi-Th-Cortex-D2.

Figure 4—figure supplement 2

Download asset Open asset

All 3-node-motifs in CBG network.

Potential oscillating motifs behind these subnetworks are marked with different colors. Yellow: motif Proto-STN; Orange: motif STN-GPi-Th-cortex; Blue: motif Proto-Arky-D2; Green: motif Proto-FSN-D2; Purple: motif Proto-GPi-Th-Cortex-D2.

Figure 4—figure supplement 3

Download asset Open asset

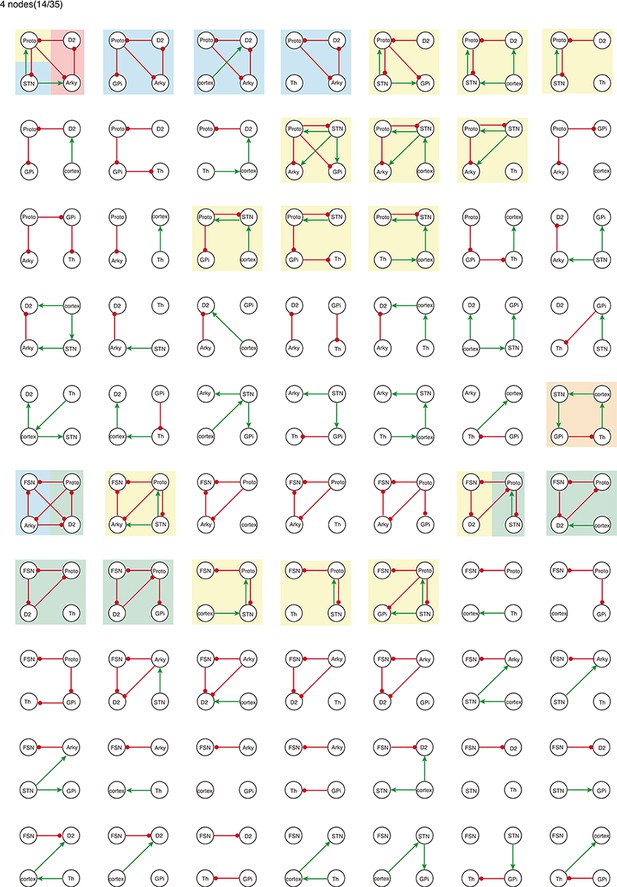
All 4-node-motifs in CBG network.

Potential oscillating motifs behind these subnetworks are marked with different colors. Yellow: motif Proto-STN; Orange: motif STN-GPi-Th-cortex; Blue: motif Proto-Arky-D2; Green: motif Proto-FSN-D2; Purple: motif Proto-GPi-Th-Cortex-D2.

Figure 4—figure supplement 4

Download asset Open asset

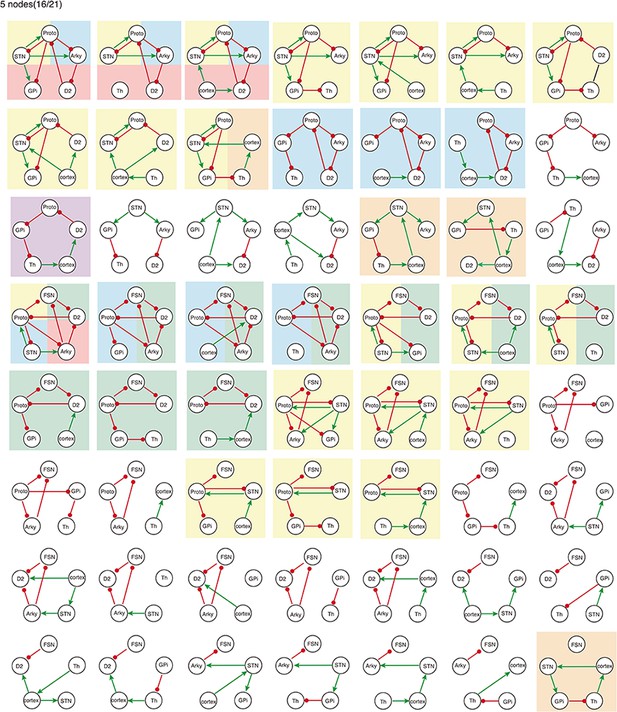
All 5-node-motifs in CBG network.

Potential oscillating motifs behind these subnetworks are marked with different colors. Yellow: motif Proto-STN; Orange: motif STN-GPi-Th-cortex; Blue: motif Proto-Arky-D2; Green: motif Proto-FSN-D2; Purple: motif Proto-GPi-Th-Cortex-D2.

Figure 4—figure supplement 5

Download asset Open asset

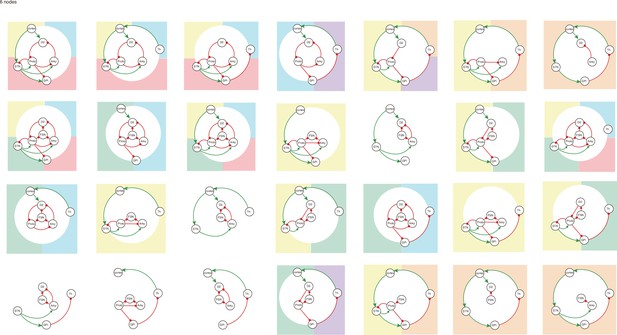
All 6-node-motifs in CBG network.

Potential oscillating motifs behind these subnetworks are marked with different colors. Yellow: motif Proto-STN; Orange: motif STN-GPi-Th-cortex; Blue: motif Proto-Arky-D2; Green: motif Proto-FSN-D2; Purple: motif Proto-GPi-Th-Cortex-D2. labelfig:bg6nodes.

Figure 4—figure supplement 6

Download asset Open asset

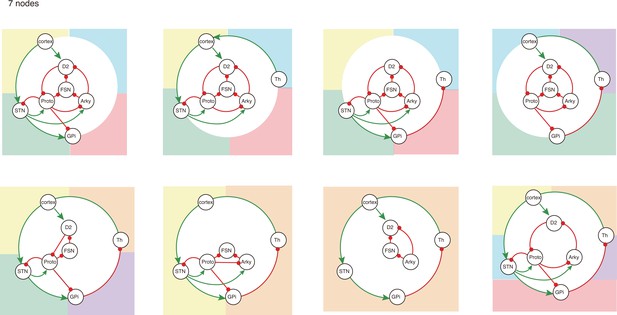
All 7-node-motifs in CBG network.

Potential oscillating motifs behind these subnetworks are marked with different colors. Yellow: motif Proto-STN; Orange: motif STN-GPi-Th-cortex; Blue: motif Proto-Arky-D2; Green: motif Proto-FSN-D2; Purple: motif Proto-GPi-Th-Cortex-D2.

Figure 5

Download asset Open asset

Oscillations in a leaky integrate-and-fire (LIF) spiking neuronal network model of specific BG motifs.

(a-b) Average peristimulus time histograms (PSTH) of all neurons in a Proto-FSN-D2 and (b) Proto-Arky-D2 motifs under Parkinson condition with power spectral density (PSD) at the top right. (c) PSTH of Proto and STN in a BG subnetwork with motif Proto-Arky-D2 as the oscillator during different STN inhibition. (d) Same thing as (c) but changing the oscillator from Proto-Arky-D2 to Proto-STN.

Tables

Table 1

Parameters of III network for Figure 3, Figure 3—figure supplement 1.

Populations	Synaptic weights			External input	Delay
Populations	I1	I2	I3	External input	Delay
I1	0(−20−0)	0	−15(−20−0)	6(0−20)	0(0−10)
I2	−15(−20−0)	0(−20−0)	0	6(0−20)	0(0−10)
I3	0	−15(−20−0)	0(−20−0)	6(0−20)	0(0−10)

Note: The range in parentheses indicates the variety of parameters when controlled.

Table 2

Parameters of EII network for Figure 3.

Populations	Synaptic weights			External input	Delay
Populations	E1	I1	I2	External input	Delay
E1	0	0	−15(−20−0)	6	0(0−10)
I1	−15(−20−0)	0(−20−0)	0	6(0−20)	0(0−10)
I2	0	−15(−20−0)	0(−20−0)	6(0−20)	0(0−10)

Note: The range in parentheses indicates the variety of parameters when controlled.

Table 3

Parameters for Figure 4 (Wilson-Cowan model).

Populations	Synaptic weights				External input	Delay
Populations	(D2)	(Arky)	(Proto)	(STN)	External input	Delay
(D2)	0	−15	0	0	4(0−20)	2
(Arky)	0	0	−15	15	3	2
(Proto)	−15	0	−8	15	1/4	2
(STN)	0	0	−15	5	4(0−20)	2

The external input to Proto is 1 in Figure 4c and 4d while it was changed into 4 in Figure 4e to help motif Proto-Arky-D2 oscillate.

Appendix 2—table 1

Parameters for the EI network in Figure 3 (Wilson-Cowan model).

Populations	Synaptic Weights (E)	Synaptic Weights (I)	External Input	Delay
E	10 (0–20)	–15 (−20–0)	6 (0–20)	2 (0–10)
I	15 (0–20)	–10 (−20–0)	0	2 (0–10)

Appendix 2—table 2

Parameters of D2-SPN neurons (LIF model with conductance-based synapses).

Name	Value	Description
$V_{r e s e t}$	–85.4 mV	Reset value for $V_{m}$ after a spike
$V_{t h}$	–45 mV	Spike threshold
$τ_{s y n}^{e x}$	0.3ms	Rise time of excitatory synaptic conductance
$τ_{s y n}^{i n}$	2ms	Rise time of inhibitory synaptic conductance
$E_{L}$	–85.4 mV	Leak reversal potential
$E_{e x}$	0 mV	Excitatory reversal potential
$E_{i n}$	–64 mV	Inhibitory reversal potential
$I_{e}$	0 pA	External input current
$C_{m}$	157 pF	Membrane capacitance
$g_{L}$	6.46 nS	Leak conductance
$t_{r e f}$	2ms	Duration of the refractory period

Appendix 2—table 3

Parameters of FSN neurons (LIF model with conductance-based synapses).

Name	Value	Description
$V_{r e s e t}$	–65 mV	Reset value for $V_{m}$ after a spike
$V_{t h}$	–54 mV	Spike threshold
$τ_{s y n}^{e x}$	0.3ms	Rise time of excitatory synaptic conductance
$τ_{s y n}^{i n}$	2ms	Rise time of inhibitory synaptic conductance
$E_{L}$	–65 mV	Leak reversal potential
$E_{e x}$	0 mV	Excitatory reversal potential
$E_{i n}$	–76 mV	Inhibitory reversal potential
$I_{e}$	0 pA	External input current
$C_{m}$	700 pF	Membrane capacitance
$g_{L}$	16.67 nS	Leak conductance
$t_{r e f}$	2ms	Duration of the refractory period

Appendix 2—table 4

Parameters of STN neurons (LIF model with conductance-based synapses).

Name	Value	Description
$V_{r e s e t}$	–70 mV	Reset value for $V_{m}$ after a spike
$V_{t h}$	–64 mV	Spike threshold
$τ_{s y n}^{e x}$	0.33ms	Rise time of excitatory synaptic conductance
$τ_{s y n}^{i n}$	1.5ms	Rise time of inhibitory synaptic conductance
$E_{L}$	–80.2 mV	Leak reversal potential
$E_{e x}$	–10 mV	Excitatory reversal potential
$E_{i n}$	–84 mV	Inhibitory reversal potential
$I_{e}$	1 pA	External input current
$C_{m}$	60 pF	Membrane capacitance
$g_{L}$	10 nS	Leak conductance
$t_{r e f}$	2ms	Duration of the refractory period

Appendix 2—table 5

Parameters of Proto and Arky neurons (LIF model with AdEx).

Name	Proto	Arky	Description
a	2.5 nS	2.5 nS	Subthresholded adaptation
b	105 pA	70 pA	Spike-triggered adaptation
$Δ_{T}$	2.55ms	1.7ms	Slope factor
$τ_{w}$	20ms	20ms	Adaptation time constant
$V_{r e s e t}$	–60 mV	–60 mV	Reset value for $V_{m}$ after a spike
$V_{t h}$	–54.7 mV	–54.7 mV	Spike threshold
$τ_{s y n}^{e x}$	1 ms	4.8ms	Rise time of excitatory synaptic conductance
$τ_{s y n}^{i n}$	5.5ms	1 ms	Rise time of inhibitory synaptic conductance
$E_{L}$	–55.1 mV	–55.1 mV	Leak reversal potential
$E_{e x}$	0 mV	0 mV	Excitatory reversal potential
$E_{i n}$	–65 mV	–65 mV	Inhibitory reversal potential
$I_{e}$	1 pA	12 pA	Constant input current
$C_{m}$	60 pF	40 pF	Membrane capacitance
$g_{L}$	1 nS	1 nS	Leak conductance
$t_{r e f}$	2ms	2ms	Duration of the refractory period

Appendix 2—table 6

Synaptic conductance weight and delay parameters in LIF model.

Synapse	Value (nS)	Delay	Value (ms)
$J_{D 2}^{D 2}$	-0.35	$Δ_{D 2}^{D 2}$	1.7
$J_{D 2}^{F S N}$	-2.6 nS	$Δ_{D 2}^{F S N}$	1.7
$J_{D 2}^{A r k y}$	-0.04 nS	$Δ_{D 2}^{A r k y}$	7
$J_{F S N}^{F S N}$	-0.4 nS	$Δ_{F S N}^{F S N}$	1.7
$J_{F S N}^{A r k y}$	-0.25 nS	$Δ_{F S N}^{A r k y}$	7
$J_{F S N}^{P r o t o}$	-1 nS	$Δ_{F S N}^{P r o t o}$	7
$J_{P r o t o}^{P r o t o}$	-1.3 nS	$Δ_{P r o t o}^{P r o t o}$	1
$J_{P r o t o}^{D 2}$	-1.08 nS	$Δ_{P r o t o}^{D 2}$	7
$J_{P r o t o}^{S T N}$	0.175 nS	$Δ_{P r o t o}^{S T N}$	2
$J_{A r k y}^{A r k y}$	-0.11 nS	$Δ_{A r k y}^{A r k y}$	1
$J_{A r k y}^{P r o t o}$	-0.35 nS	$Δ_{A r k y}^{P r o t o}$	1
$J_{A r k y}^{S T N}$	0.24 nS	$Δ_{A r k y}^{S T N}$	2
$J_{S T N}^{P r o t o}$	-0.3 nS	$Δ_{S T N}^{P r o t o}$	1

Appendix 2—table 7

Number of connections on each neuron and constant input current for Figure 5c (LIF model).

Populations	D2	Arky	Proto	STN	Constant input current (pA)
D2	504	100	0	0	0
Arky	0	5	50	30	50
Proto	500	0	25	30	50
STN	0	0	30	0	1/–49/–99

Note: To simulate the increasing inhibition to STN, the constant input current to STN was changed from 1 pA to –49 pA and then to –99 pA.

Appendix 2—table 8

Number of connections on each neuron and constant input current for Figure 5d (LIF model).

Populations	D2	Arky	Proto	STN	Constant input current (pA)
D2	504	10	0	0	0
Arky	0	5	25	30	1
Proto	500	0	25	150	–10
STN	0	0	150	0	30/–10/–80

Note: To simulate the increasing inhibition to STN, the constant input current to STN was changed from 30 pA to –10 pA and then to –50 pA.

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/88777/elife-88777-mdarchecklist1-v1.pdf
Download elife-88777-mdarchecklist1-v1.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Jie Zang
Shenquan Liu
Pascal Helson
Arvind Kumar

(2024)

Structural constraints on the emergence of oscillations in multi-population neural networks

eLife 12:RP88777.

https://doi.org/10.7554/eLife.88777.3

Share this article

Cite this article

Structural condition for oscillations: odd inhibitory cycle rule and its illustrations.

The intuitive explanations of Theorem 1 and 2.

Influence of network properties on the oscillation frequency in motifs III and EII with Wilson-Cowan model.

Influence of III network properties on the oscillation frequency in Wilson-Cowan model.

Effect of synaptic delays on motifs with even inhibition in the Wilson-Cowan model.

Influence of EI network properties on the oscillation frequency in Wilson-Cowan model.

Schematic of CBG network model with potential oscillators and the interaction between two oscillators in Wilson-Cowan model.

All 2-node-motifs in CBG network.

All 3-node-motifs in CBG network.

All 4-node-motifs in CBG network.

All 5-node-motifs in CBG network.

All 6-node-motifs in CBG network.

All 7-node-motifs in CBG network.

Oscillations in a leaky integrate-and-fire (LIF) spiking neuronal network model of specific BG motifs.

Parameters of III network for Figure 3, Figure 3—figure supplement 1.

Parameters of EII network for Figure 3.

Parameters for Figure 4 (Wilson-Cowan model).

Parameters for the EI network in Figure 3 (Wilson-Cowan model).

Parameters of D2-SPN neurons (LIF model with conductance-based synapses).

Parameters of FSN neurons (LIF model with conductance-based synapses).

Parameters of STN neurons (LIF model with conductance-based synapses).

Parameters of Proto and Arky neurons (LIF model with AdEx).

Synaptic conductance weight and delay parameters in LIF model.

Number of connections on each neuron and constant input current for Figure 5c (LIF model).

Number of connections on each neuron and constant input current for Figure 5d (LIF model).

MDAR checklist

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)