Implications of variable synaptic weights for rate and temporal coding of cerebellar outputs
- Department of Neurobiology, Harvard Medical School, United States
- Department of Neural and Behavioral Sciences, Pennsylvania State University College of Medicine, United States
Figures
Figure 1
The amplitudes of Individual Purkinje cell (PC) to cerebellar nuclei (CbN) inputs are highly variable.
Unitary PC-CbN IPSCs were recorded in brain slices. The data in (a–c) were obtained for this study. The histogram of input sizes in (d–e) were based on new experiments (d, n = 44; e, n = 39), on Turecek et al., 2017 (e, n = 44), and Khan et al., 2022 (d, n = 30). (a) Example of a small PC-CbN input (P27). Top: responses evoked with the same stimulus intensity are superimposed for 40 trials (gray), and the average of successes (black) and failures (blue) is shown. Bottom: IPSCs’ amplitudes are plotted as a function of trial number. (b) As in (a), but for a medium-size input onto the same cell. (c) As in (a), but for a large-size input onto the same cell. (d) Distribution of input sizes for PC-CbN IPSCs in young mice (P10–P20, n = 74). (e) Distribution of input sizes for PC-CbN IPSCs in juvenile mice (P10–P20, n = 83). (f) Normalized cumulative plot of conductances. The distributions of unitary input sizes in P10–20 animals and P23–32 animals were significantly different (p<0.0001) with a Kolmogorov–Smirnov test.
-
Figure 1—source data 1
PC-CbN unitary IPSCs and conductances.
- https://cdn.elifesciences.org/articles/89095/elife-89095-fig1-data1-v1.xlsx
Figure 2 with 3 supplements
Large Purkinje cell (PC) inputs powerfully influence cerebellar nuclei (CbN) neuron firing.
Dynamic clamp experiments and simulations were conducted with variable distribution of PC input sizes. (a) The corrected distributions of PC-CbN input sizes in juvenile animals (f, red) were approximated with 16 small inputs (3 nS, green), 10 medium inputs (10 nS, blue), and 2 large inputs (30 nS, red). Raster plots are shown for the spike times of the 16 small (green), 10 medium (blue), and 2 large (red) inputs used in dynamic clamp experiments. (b) The total conductance waveform is shown (black) along with contributions from small (green), medium (blue), and large (red) inputs. (c) Spikes in a CbN neuron evoked by the total conductance in (b) in dynamic clamp experiments. (d) The normalized cross-correlograms of input spiking and CbN neuron spiking for small, medium, and large inputs for dynamic clamp experiments. Different cells (n = 6, gray) are shown along with the average cross-correlograms (colored traces). (e) Summary of the excitation (e), inhibition (i), and half-decay time (t1/2), as defined in the inset for the data in (d). Inset shows how the parameters are determined. (f) Cumulative histogram of all recorded inputs from Figure 1 for P23–32 mice corrected for depression and internal solution (red), the simplified input distribution used in dynamic clamp studies in a (gray), and inputs drawn from that distribution that were used in a simulation (black). (g) Calculated cross-correlograms (normalized) for each of the different inputs used in a simulation. (h) Summary of the excitation (e), inhibition (i), and half-decay time (t1/2), for a simulation as defined in the inset for the simulated cell in (g) (black), and for inputs to nine other simulated cells with different distributions of inputs (gray). The summary data are shown as the mean ± SEM.
-
Figure 2—source data 1
Cross-correlograms and input sizes.
- https://cdn.elifesciences.org/articles/89095/elife-89095-fig2-data1-v1.xlsx
Figure 2—figure supplement 1
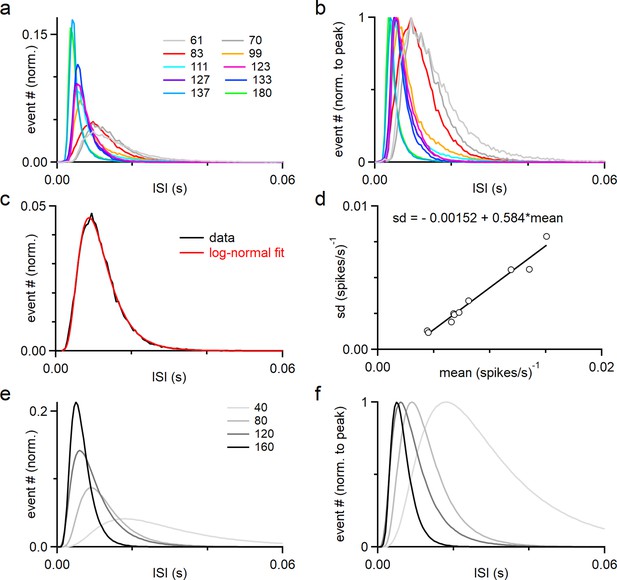
Interspike interval (ISI) histograms of Purkinje cells (PCs) firing used in this study.
(a) Normalized ISI histograms of 10 PCs recorded in vivo from our previous studies (Han et al., 2020), with their average firing rates indicated in the legend. (b) As in (a) but normalized to the peak. (c) Example of a lognormal distribution fitting (red) to the ISI histogram of one PC recorded in vivo (black, 83 Hz). Similar fittings were performed for the other nine PCs. (d) The standard deviation (sd) as a function of the mean of the lognormal distribution fits to the 10 PCs was fitted as a linear function. Fits were performed in IGOR Pro to the function.. The values of μ and σ for standard lognormal distribution are computed from and width using equations: μ = , σ = The values of mean and sd of the lognormal distribution fits were computed from μ and σ using equations: mean = and sd = . This linear function was used to determine the parameters for a PC firing ISI lognormal distribution with a desired firing rate. (e) Four lognormal distributions representing artificial PC firing ISI distributions with different firing rates generated with the mean and sd from the linear function in (d). (f) As in (e) but normalized to the peak.
Figure 2—figure supplement 2
Further explanations of the dynamic clamp experiments and simulations.
(a) Related to Figure 2a. Raster plots of 16 small inputs (green), 10 medium inputs (blue), and 2 large inputs (red) that fire at 83 Hz. (b) Related to Figure 2b. Unitary Purkinje cell–cerebellar nuclei (PC-CbN) input waveforms with the indicated sizes. The spikes from each different-size inputs in (a) were convolved with the respective waveform to obtain the total inhibitory conductance shown in Figure 2b. (c) Similar as (a) but for a simulation with 19 inputs, with their size distributed indicated in Figure 2f. (d) Unitary PC-CbN input waveforms with the largest size and smallest size from the simulation. The raster plot of each PC input was convolved with the appropriate size conductance waveform to obtain its contribution to the inhibitory conductance, and the total inhibitory conductance was computed by summing the conductances of all inputs.
Figure 2—figure supplement 3
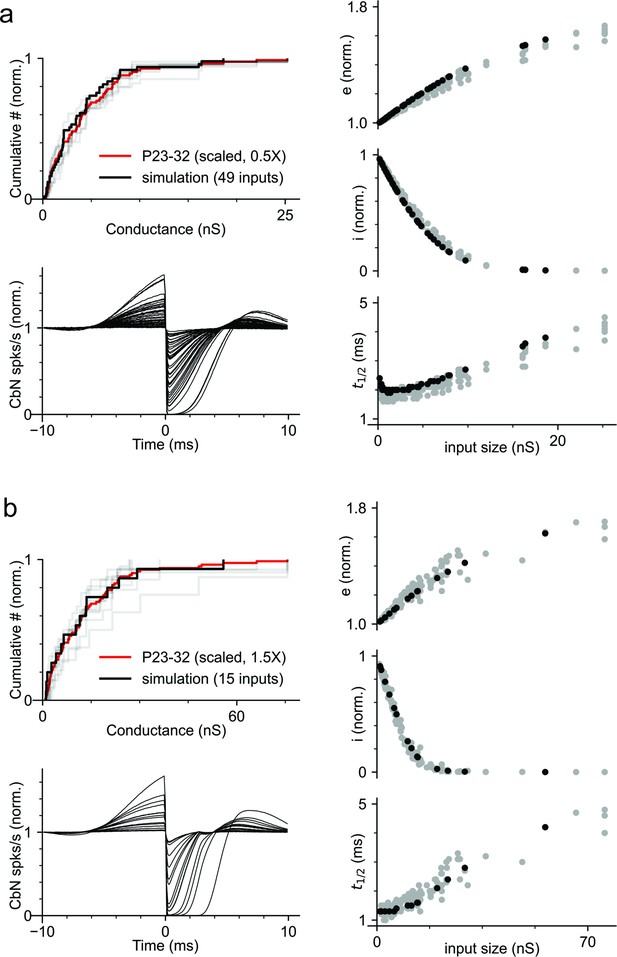
Extra simulations with different scaling factors of the unitary Purkinje cell–cerebellar nuclei (PC-CbN) conductances.
(a) Similar to the simulation in Figure 2f–h, but with a scaling factor of 0.5. (b) Similar to the simulation in Figure 2f–h, but with a scaling factor of 1.5.
Figure 3 with 1 supplement
Autocorrelation of Purkinje cell (PC) firing leads to excitation prior to inhibition of cerebellar nuclei (CbN) neurons.
Dynamic clamp experiments were conducted using PCs with different firing statistics. (a) Interspike interval (ISI) histograms for three different PCs recorded in vivo (left), and for an artificial Poisson input lacking a refractory period (right). (b) Autocorrelation functions for the ISI distributions in (a). At 0 ms, all graphs peak at 1 and graphs are truncated to allow better visualization. (c) Calculated spike-triggered average inhibitory conductances for different cases (12 × 20 nS at 49 Hz, 9 × 20 nS at 83 Hz, 6 × 20 nS at 122 Hz, and 9 × 20 nS for Poisson inputs), with ISIs drawn from the corresponding distributions in (a). (d) Cross-correlograms are shown for PC inputs and CbN spiking for dynamic clamp experiments that used the distributions in (a).
Figure 3—figure supplement 1
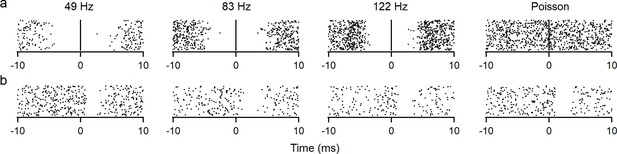
Raster plots of the autocorrelations and cross-correlations.
(a) Relevant to Figure 3b. Raster plots showing 500 sweeps of autocorrelations of Purkinje cells (PCs) firing at different frequencies and PCs firing in a Poisson fashion. The refractoriness of PC firing reflects their firing statistics. (b) Relevant to Figure 3d. Raster plots showing 500 sweeps of the spike trains of a cerebellar nuclei (CbN) neuron surrounding same-sized PC inputs firing at different frequencies and PCs firing in a Poisson fashion. The elevation of CbN neuron firing prior to the timing of the PC input is most apparent for rapidly firing inputs and is absent from the Poisson input that lacks a refractory period.
Figure 4
The amplitudes and fluctuations of the total inhibitory conductance both regulate the firing of cerebellar nuclei (CbN) neurons.
Dynamic clamp experiments and simulations were conducted with varied amplitudes and fluctuations in the total inhibitory conductance. (a) CbN neuron spiking observed for constant inhibitory conductances of the indicated amplitudes. (b) Summary of CbN neuron firing rates (n = 7 cells) during constant inhibitory conductances as in (a). (c) Inhibitory conductances with the same average conductance (56 nS) are shown for a constant conductance (far left) and for different cases with the numbers and sizes of inputs varied. (d) CbN neuron spiking is shown for dynamic clamp experiments with the inhibitory conductances in (c). (e) The coefficient of variation (CV) of the inhibitory conductance is plotted as a function of the input size. (f) CbN firing rate is plotted as a function of input size. (g) CbN firing rate is plotted as a function of the CV of the inhibitory conductance. (h) Normalized cumulative plots of conductances of three different input distributions (solid lines) drawn from the observed distribution (Figure 2f, red) and for the 40 × 5 nS inputs (dashed line). (I) CbN firing rates in dynamic clamp experiments that used the inhibitory conductances in (h) are plotted as a function of the CV of the inhibitory conductance. (j) Simulated CbN firing rates based on 1000 different input distributions randomly drawn from the observed distribution of input sizes (filled gray) and for 40 × 5 nS inputs (open circle) are plotted as a function of the CV of the inhibitory conductance. The three distributions used in dynamic clamp experiments in (i) are highlighted. The summary data are shown as the mean ± SEM.
-
Figure 4—source data 1
Different distributions and CbN neuron firing rates.
- https://cdn.elifesciences.org/articles/89095/elife-89095-fig4-data1-v1.xlsx
Figure 5 with 2 supplements
Purkinje cell (PC) inputs effectively convey an inverse rate code.
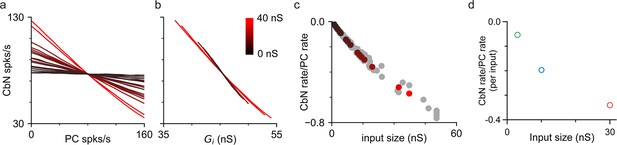
Simulations and dynamic clamp experiments were conducted with the firing rates of PC inputs varied. (a) Simulations with different-size inputs drawn from the distribution in Figure 2f and the firing rates of each input were varied. The firing rates of cerebellar nuclei (CbN) neurons are plotted as a function of the firing rate of the varied PC input, with the color indicating the input size. (b) The firing rates of CbN neurons in (a) are plotted as a function of the total inhibitory conductance (Gi) resulting from varying the firing rate of each PC input. The color scale is the same as in (a). (c) The slopes of CbN output firing rates vs. PC input firing rates are plotted for different-size inputs for the simulated CbN neuron in (a) and (b) (black), and nine other neurons with different input size distributions (gray). (d) Dynamic clamp experiments were performed with small (16 × 3 nS, green), medium (10 × 10 nS, blue), and large (2 × 30 nS, red) inputs. The firing rates of either all small, all medium, or all large inputs were varied (Figure 5—figure supplement 2). The slope of CbN output firing rate vs. PC input firing rate divided by the number of inputs is plotted for different-size inputs.
-
Figure 5—source data 1
Simulations and dynamic clamp experiments for rate codes.
- https://cdn.elifesciences.org/articles/89095/elife-89095-fig5-data1-v1.xlsx
Figure 5—figure supplement 1
Simulations with different scaling factors of the unitary Purkinje cell–cerebellar nuclei (PC-CbN) conductances.
(A) Similar to the simulation in Figure 5a–c, but with a scaling factor of 0.5 for the input sizes. (a) Simulations with different-size inputs drawn from the distribution in Figure 2f and the firing rates of each input were varied. (b) The firing rates of CbN neurons in (a) are plotted as a function of the total inhibitory conductance (Gi) resulting from varying the firing rate of each PC input. (c) The slope of CbN output firing rate vs. PC input firing rate is plotted for different inputs for the simulated CbN neuron in (a) and (b) (black), and for nine other neurons with different input distributions (gray). (B) As in (A), but with a scaling factor of 1.5 for the input sizes.
Figure 5—figure supplement 2
Dynamic clamp experiments with small (16 × 3 nS, green), medium (10 × 10 nS, blue), and large (2 × 30 nS, red) inputs.
The firing rates of either small, medium, or large Purkinje cell (PC) inputs were varied from 0 to 160 spikes/s. (a) The firing rates of either small (green), medium (blue), or large (red) inputs were varied every 2 s while the firing rates of the other inputs were maintained at 80 spikes/s. (b) The resulting average inhibitory conductances for the three different conditions are shown. (c) The resulting average coefficient of variation (CV) of the inhibitory conductances is shown. (d) The firing rates of cerebellar nuclei (CbN) neurons with the conductances in (a–c) are shown as individual cells (n = 9, gray) and their average (black). (e) Quantification plot for (b). Total inhibitory conductance is plotted as a function of the firing rate of the varied PC inputs. Elevating the firing rates of all size inputs increased the amplitude of the total inhibitory conductance. Varying the firing rate of all medium inputs had larger effects because of their larger contribution to the inhibitory conductance. (f) Quantification plot for (c). The CV of the total inhibitory conductance is plotted as a function of the firing rate of the varied PC inputs. Eliminating the firing of either the small or medium inputs increased the CV of the inhibitory conductance, whereas eliminating the firing of the large inputs decreased the CV of the inhibitory conductance. (g) Quantification plot for (d). The firing rates of CbN neurons are plotted as a function of the firing rate of the varied PC inputs. (h) The firing rates of CbN neurons are plotted as a function of the total inhibitory conductance (Gi). (I) The firing rates of CbN neurons are plotted as a function of the CV of total inhibitory conductance (Gi CV). The summary data are shown as the mean ± SEM.
Figure 6
The influence of Purkinje cell (PC) synchrony on the firing rates of cerebellar nuclei (CbN) neurons for uniform- and variable-size PC inputs.
Dynamic clamp experiments were conducted with either uniform (a) or variable inputs (b) in which the conductance was kept constant, but the synchrony of the inputs was varied. (a) (i) The extent of synchrony of uniform-size inputs (40 × 5 nS) is varied. (ii) The inhibitory conductance in which the synchrony of inputs is varied as in (a). (iii) The coefficient of variation (CV) of the inhibitory conductance. (iv) CbN neuron firing rate with the conductance (average, black; individual cells, n = 14, gray). (v) The normalized firing rate for the cells in (iv). (b) Similar experiments were performed on the same cells as in (a), but for inputs of variable-sizes (small: 16 × 3 nS, green; medium: 12 × 8 nS, blue; large: 2 × 30 nS, red). In some cases, all types of inputs were synchronized (purple), in others only the small inputs (green) or the medium inputs (blue) were synchronized. (c) CbN neuron firing rate as a function of the percentage of synchronous inputs. (d) CbN neuron firing rate as a function of the total amplitude of synchronous inputs. (e) The normalized CbN firing rates as a function of the amplitude of the synchronized inputs. (f) CbN neuron firing rate as a function of the CV of the inhibitory conductances. (g–j) Similar plots to (c–f), but for simulations with different-size inputs (dark purple, based on a single distribution, light purple based on nine other different distributions) and uniform inputs (40 × 5 nS, black circles). (k) Violin plots showing the simulated CbN neuron firing rate with 100 different distributions of different-size inputs (not syn), and the two largest inputs or the two smallest inputs synchronized. (l) As in (k) but normalized to the nonsynchronized firing rate. The summary data are shown as the mean ± SEM.
-
Figure 6—source data 1
Dynamic clamp experiments and simulations for syncrony.
- https://cdn.elifesciences.org/articles/89095/elife-89095-fig6-data1-v1.xlsx
Figure 7
The influence of Purkinje cell (PC) synchrony on the spike timing of cerebellar nuclei (CbN) neurons for uniform- and variable-size PC inputs.
(a) Top: the cross-correlograms of PC input and CbN neuron spiking for nonsynchronous inputs (left) and 50% synchronous inputs (right) with uniform-size inputs. Individual cells (gray) and averages (black) are shown. Lower: as above, but normalized to the baseline firing rate. (b) As in (a) but for different-size inputs (as in Figure 6). The cross-correlograms of small (green), medium (blue), and large (red) inputs for unsynchronized inputs (left) and 50% synchronous inputs (right, purple) are shown. (c) Summary plots of the excitation (e), inhibition (I) as a function of the amplitude of synchronized inputs. (d) As in (c) but for half-decay time (t1/2). (e, f) As in (c, d), but for simulations. The summary data are shown as the mean ± SEM.
-
Figure 7—source data 1
Cross-correlograms for synchrony.
- https://cdn.elifesciences.org/articles/89095/elife-89095-fig7-data1-v1.xlsx
Figure 8
The influence of Purkinje cell (PC) pauses on the firing of cerebellar nuclei (CbN) neurons for uniform- and variable-size PC inputs.
Dynamic clamp experiments and simulations were conducted with either uniform or variable inputs in which different percentages of PC inputs were paused for 2 ms. (a) Normalized cumulative plots of conductances of PC inputs for a uniform (40 × 5 nS, dashed line) and a variable distribution (purple). (b) Raster plot shows example spiking for 40 PC inputs with spikes eliminated in a 2-ms period (gray region) in 50% of the PCs. (c) Normalized histograms showing the relative changes in CbN neurons firing for uniform (black) and variable (colored) PC inputs, when PC inputs were paused for 2 ms in 25 and 50% of the inputs. For variable inputs, three different populations of inputs were paused: the smallest, those in the middle of the distribution, and the largest inputs. Average values (bold) and individual cells (faint lines, n = 8) are shown. (d) The normalized CbN firing rates as a function of the percentage of paused inputs for uniform (black symbols fit with solid black line) and variable inputs (colored). (e) The normalized CbN firing rates as a function of the total amplitude of paused inputs for uniform (black) and variable inputs (colored). Fits are shown for uniform inputs (solid black line) and variable inputs (dashed line). (f) As in (e), but for simulations where different subsets of PC inputs were paused for 2 ms. (g) The normalized overall CbN firing rates as a function of the total amplitude of paused inputs for uniform (black) and variable (purple) inputs from a simulation where different subsets of PC inputs were paused for 2 ms every 50 ms. Fits are shown for uniform inputs (solid black line) and variable inputs (dashed purple line). The summary data are shown as the mean ± SEM.
-
Figure 8—source data 1
Dynamic clamp experiments and simulations for PC pauses.
- https://cdn.elifesciences.org/articles/89095/elife-89095-fig8-data1-v1.xlsx
Figure 9
The main consequences of having variable-size Purkinje cell–cerebellar nuclei (PC-CbN) synaptic inputs.
(a) Left: schematic showing that CbN neurons are innervated by numerous PCs that have very different input strengths. Right: examples of unitary inhibitory conductances from PCs that range in size from very weak (green), medium-sized (blue), to strong (red) (adapted from Figure 1a–c). (b) CbN neuron firing rate as a function of input PC firing rate showing linear rate code conveyed by a weak (green) and a strong (red) PC input. (c) PC-CbN neuron cross-correlograms show the effects of a weak (green) and a strong (red) PC input. A single strong PC input is highly effective at controlling CbN neuron firing on rapid time scales. As expected, PCs transiently suppress CbN neuron firing, but there is also a preceding increase in CbN firing that arises from the statistics of PC firing and their refractory periods. (d) For the same total inhibition, the variability of the total inhibitory conductance is much larger for variable-size inputs than for uniform input sizes. (e) Compared to uniform-sized inputs, variable PC input sizes increase the baseline firing rate of CbN neurons as a result of elevated variability in the total inhibitory conductance (d). This has important secondary consequences. For variable PC input sizes, elevated basal CbN neuron firing rates reduce the ability of synchronizing or transiently pausing PC firing to promote CbN neuron firing.
Tables
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Strain, strain background (Mus musculus) | C57BL/6 | Charles River Laboratories | N/A | |
| Chemical compound, drug | NBQX disodium salt | Abcam | Ab120046 | |
| Chemical compound, drug | (R,S)-CPP | Abcam | Ab120160 | |
| Chemical compound, drug | Strychnine hydrochloride | Abcam | Ab120416 | |
| Chemical compound, drug | SR95531 (gabazine) | Abcam | Ab120042 | |
| Chemical compound, drug | CGP 55845 hydrochloride | Abcam | Ab120337 | |
| Chemical compound, drug | QX-314 chloride | Abcam | Ab120118 | |
| Software, algorithm | Igor Pro | WaveMetrics (https://www.wavemetrics.com/order/order_igordownloads6.htm) | RRID:SCR_000325 | Version 6.37 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Implications of variable synaptic weights for rate and temporal coding of cerebellar outputs
eLife 13:e89095.
https://doi.org/10.7554/eLife.89095
