Using recurrent neural network to estimate irreducible stochasticity in human choice behavior
- Sagol School of Neuroscience, Tel Aviv University, Israel
- TAD, Center of AI & Data Science, Tel Aviv University, Israel
- School of Psychological Sciences, Tel Aviv University, Israel
Figures
Figure 1
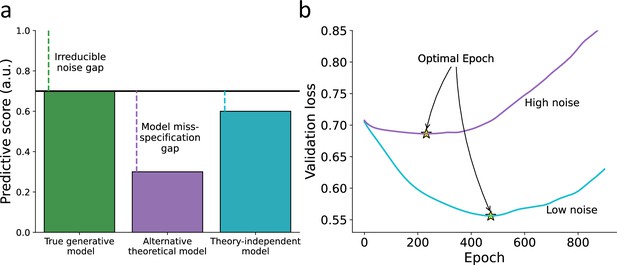
Hypothetical illustration for using theory-independent models to explore the fit of theoretical models to human behavior.
(a) Predictive performance – we illustrate the predictive gap for three hypothetical models: first, the true data-generating model (i.e., forever unknown to the researcher; green) where the remaining gap is due to an irreducible noise component in the individual’s behavior. Second, a hypothetical alternative theoretical model (e.g., specified by a researcher; purple), where the remaining predictive gap reflects both irreducible noise and model misspecification. Finally, a hypothetical theory-independent model (turquoise) is assumed to reflect a predictive gap that is mainly due to model misspecification compared with the alternative model, yet does not provide a clear theoretical interpretation. We, therefore, assume that theory-independent models can be used to inform researchers about the amount of improvement that can be further gained by assembling additional theoretical models. (b) Point of early stopping – when training a network, we can examine its performance against a validation set as a function of the number of epochs used for training the parameters (x-axis). The point of early stopping reflects the maximum number of training epochs with the best predictive performance, just before the network starts to overfit the data (i.e., learn patterns that are due to noise; indicated by a yellow star). Here, we illustrate two hypothetical learning curves reflecting the point of early stopping for low-noise (purple line) and high-noise (blue line) datasets. Specifically, we illustrate the notion that the point of early stopping can reflect the amount of noise in the data, so a lower point of early stopping reflects noisier data (considering a fixed number of observations for the two datasets and network size).
Figure 2 with 2 supplements
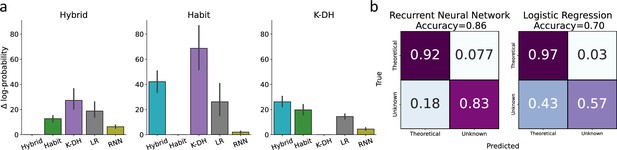
Classification of model misspecification using the predictive performance of theory-independent models.
Here, we tested our ability to identify model misspecification of theoretical models using recurrent neural network (RNN) and logistic regression. (a) Across three theoretical models (Hybrid, Habit, K-DH),we simulated 100 agents and predicted agents’ actions using the same three theoretical models, RNN and logistic regression. We present on the y-axis differences in negative log-probability estimates for each fitted model against the true generative model. For example, the left panel depicts the difference in log-probability estimates across all five models for 100 agents simulated using the hybrid model. As expected, across all three generative theoretical models, RNN achieved the best performance score, second only to the true generative theoretical model (black lines represent 95%CI). (b) We calculated a confusion matrix for a hypothetical lab that is familiar only with one theoretical model and uses RNN or logistic regression to try and conclude whether a certain agent shows a high predictive gap due to model misspecification. Each cell represents the average value across three classification rounds. We assumed one lab theoretical model as the true data-generating model in each round. Agents were then classified into two classes (assumed lab model or unknown model) based on the difference in predictive scores between the assumed theoretical model and a theory-independent model. For example, the top-left cell in the left confusion matrix indicates the percentage of agents (averaged over three classification rounds) better predicted by their true data-generating model than by the RNN. Results show good classification by RNN (accuracy ≈ 0.86), and logistic regression (accuracy ≈ 0.70), with better performance for RNN compared with logistic regression. Overall, these results suggest that RNN/logistic regression can be used to some extent to inform researchers regarding model misspecification when using theoretical computational modeling.
Figure 2—figure supplement 1
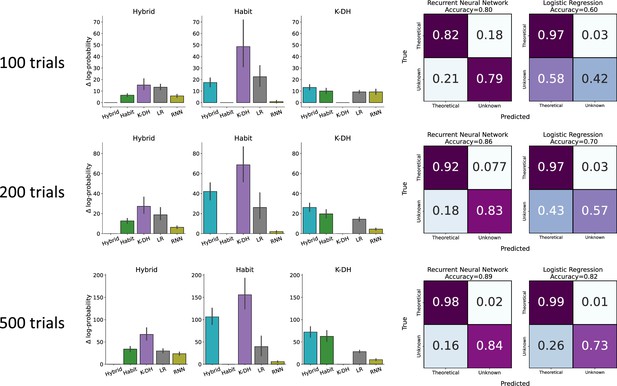
Action prediction and agent classification for different lengths of simulated trials.
Similar to Figure 2. The difference in the negative log probability obtained by each model to each group of agents (left) and classification of each agent (right) for various simulated trial lengths [100, 200 (Figure 2), 500]. Overall recurrent neural network (RNN) outperformed the logistic regression (LR) model in both predictive score and classification accuracy.
Figure 2—figure supplement 2
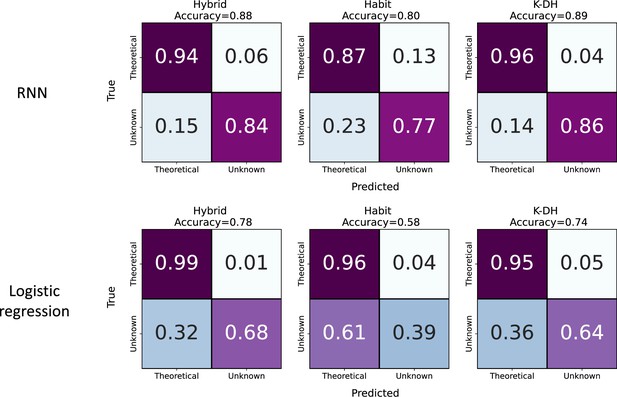
Agent classification of each hypothetical lab.
Same as Figure 2b but for each classification round (i.e., hypothetical lab) separately. Classification by recurrent neural network (RNN) (top) and classification by logistic regression (LR) (bottom). Across all theoretical models (Hybrid, Habit, and K-DH), RNN achieved a higher true negative rate (bottom-right square) compared to lLR. In addition, although RNN achieved a lower true positive rate (upper left square) compared to LR, the overall classification accuracy of the RNN model is higher.
Figure 3 with 3 supplements
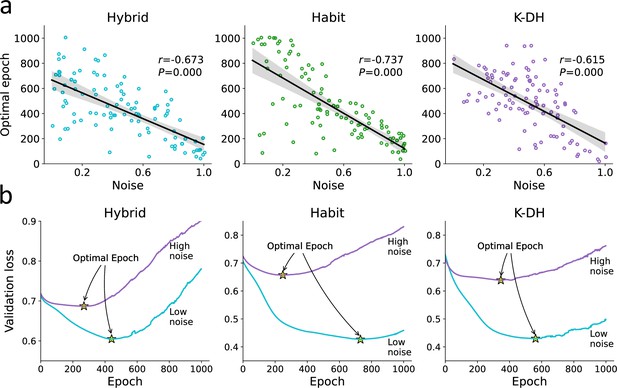
Optimal epoch relation to true noise.
For each agent, we iteratively trained the recurrent neural network (RNN) while examining its predictive ability. We then recorded for each agent the number of optimal epochs, which is the number of RNN training iterations that minimized underfitting and overfitting. (a) We found a strong association between the number of optimal RNN training epochs (y-axis) and the agent’s true noise level. This result demonstrates that the number of optimal RNN epochs can be used as a proxy for the amount of information in a certain dataset (given a fixed number of observations and network size). (b) For illustration purposes, we plotted the RNN loss curves for agents with low vs. high levels of noise. Specifically, we present loss curves where for each RNN training epoch (x-axis) we estimate the predictive accuracy using a validation dataset. We estimated the loss curves of 300 artificial agents (from three theoretical models) and divided them into two groups according to their true noise (high vs. low). We show that the point of optimal epoch (early stopping; denoted yellow star) was higher to agents with low internal noise.
Figure 3—figure supplement 1
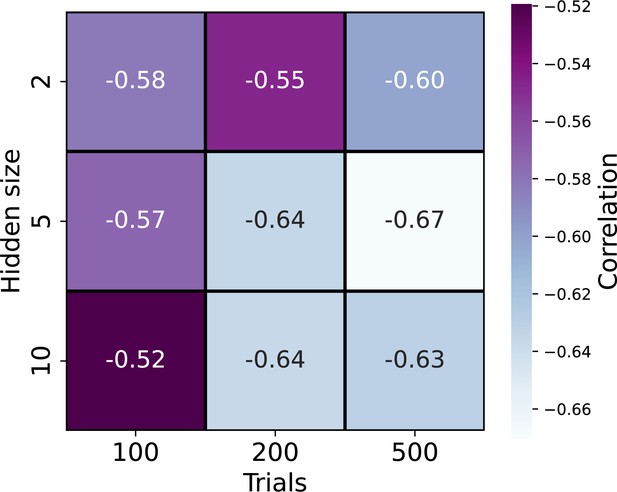
Correlation matrix between optimal epoch and the true noise.
To test how the network’s hidden size and the number of simulated trials affect the relationship between the number of optimal epochs and the true noise each agent holds, we conducted a repeated analysis similar to Study 1. Each square denotes the Pearson correlation between the number of optimal epochs and the true noise each agent holds. For each square, the correlation was calculated using agents that were simulated for 100, 200, or 500 trials (x-axis) and the recurrent neural network (RNN) model hidden layer consists of 2, 5, or 10cells in the hidden GRU layer (y-axis). We found across all combinations a negative relation such that longer training was most beneficial in predicting the action of agents with low levels of true noise.
Figure 3—figure supplement 2
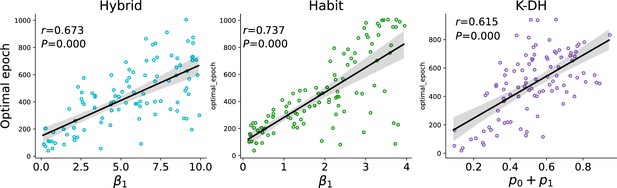
Optimal epoch relation to true noise.
Same as Figure 3a, with the noise parameter value unscaled.
Figure 3—figure supplement 3
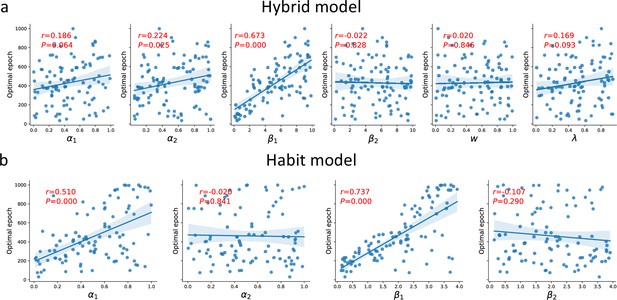
Associations between all model parameters and the optimal number of epochs.
(a) Hybrid model (parameters left to right): α learning rates in both stages, inverse-temperature β parameters (both stages), MF-MB weight parameter, and eligibility trace. (b) Habit model (parameters left to right): α learning rates in both stages and inverse-temperature β parameters (both stages). Note that recurrent neural network (RNN) was fitted only for first-stage choices; therefore, we expected only first-stage parameters to predict the number of optimal epochs.
Figure 4
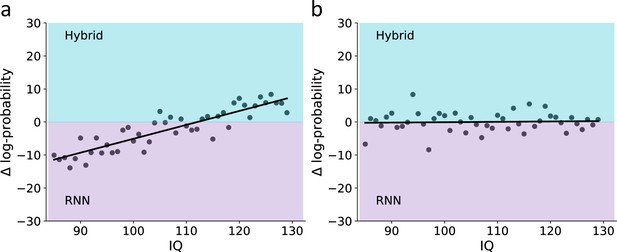
Prediction scenarios for the use of recurrent neural network (RNN) to examine model misspecification as a function of IQ.
To demonstrate the ability to use RNN to identify model misspecification, we illustrate two hypothetical associations between IQ and the difference in predictive performance for a theoretical hybrid model vs. RNN. (a) Prediction for a scenario where there is a higher frequency of model misspecification among low vs. high IQ individuals: here, we assume that low IQ participants are more frequently misspecified by the theoretical hybrid model compared with high IQ individuals. Therefore, the prediction here is that for low IQ individuals the RNN will provide higher predictive gap improvement compared with high IQ individuals. (b) Prediction for a scenario where there is equal frequency of model misspecification among low vs. high IQ individuals: here, we assume that the frequency of model misspecification is similar across levels of IQ. Therefore, we predict no association between IQ and the change in predictive accuracy for RNN vs. the theoretical hybrid model.
Figure 5 with 1 supplement
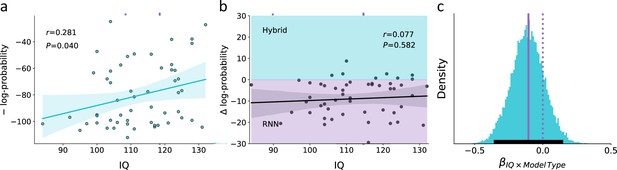
Empirical association of the predictive score for the theoretical hybrid model, recurrent neural network (RNN), and IQ.
(a) Association between IQ and the predictive score obtained from a theoretical hybrid model, showing that low IQ individuals are associated with lower predictive accuracy (shaded area corresponds to the 95% confidence interval for the regression line). We assumed that if this association is mostly due to higher rates of model misspecification in low compared with high IQ individuals, then RNN should overcome this difficulty and show similar predictive accuracy across both models. (b) Difference in the predictive score for the theoretical hybrid model vs. RNN. Across different IQ scores, we found no significant difference in the predictive score of one of the models over the other. This finding suggests that the lower predictive score of low IQ individuals is not due to systematic model misspecification, but rather due to noisier behavior (shaded turquoise/purple areas signify better predictive score of the Hybrid/RNN models, respectively; shaded dark area corresponds to the 95% confidence interval for the regression line). (c) Posterior distribution for the interaction term from a Bayesian regression, suggesting no effect for the paired interaction of model type (hybrid vs. RNN) and IQ on the model’s predictive score. This null effect suggests that the association between IQ and predictive accuracy was similar for both hybrid and RNN models (soiled/dashed purple lines indicate median/zero, respectively; lower solid black line indicates 95%HDI). These results suggest that the higher predictive gap of the theoretical model for low compared with high IQ individuals is mostly due to individual differences in the levels of behavioral noise rather than systematic model misspecification.
Figure 5—figure supplement 1
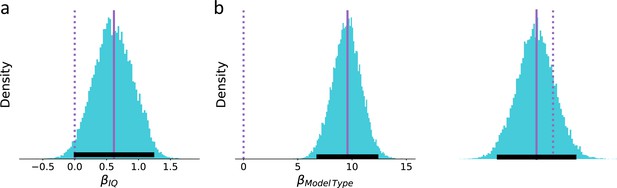
Posterior distribution for the regression coefficient.
(a) Individual’s IQ score and (b) model type on predictive log-probability scores (soiled/dashed purple lines indicate median/zero, respectively; lower solid black line indicates 95%HDI). We found two main effects of individual’s IQ and model type on predictive log-probability scores such that low IQ participant’s choices are less predictable than high IQ participant’s and that on average the recurrent neural network (RNN) model reaches a better predictive score than the hybrid model.
Figure 6
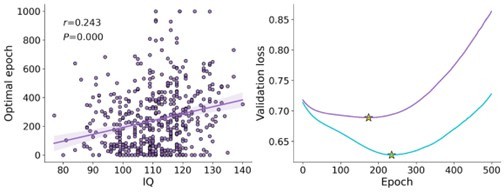
Association between IQ and individual’s optimal epoch estimates.
(a) Relation between the number of optimal recurrent neural network (RNN) training epochs (y-axis) and IQ score (x-axis; shaded area corresponds to the 95% confidence interval for the regression line). We found that IQ significantly correlates with individuals’ optimal RNN epoch estimates, such that lower IQ participants required fewer RNN training epochs to reach the optimal training point. (b) Loss curve of validation data averaged over the low IQ group (IQ < 110; purple) and high IQ group (IQ > 110; turquoise). The point of optimal epoch (early stopping) is denoted by a yellow star. We found that the optimal epoch for the high IQ group was significantly higher than that for the low IQ group. Overall, when combined with our simulation study demonstrating the association between the number of optimal RNN epochs and true noise (for a fixed number of observations and network size; see Figure 3), these results suggest noisier decision-making for low IQ individuals compared to high IQ individuals. This finding, along with the results obtained from the RNN predictive accuracy (see Figure 5), suggests that low IQ individuals are not more frequently misspecified compared to their high IQ peers.
Figure 7
Two-step task.
(a) At the first stage, participants choose between two options (A or B) that probabilistically lead to one of two second-stage states, with a fixed transition probability of 70% (‘common’) or 30% (‘rare’). In the second stage, participants choose between two options (C/D or E/F) to obtain rewards. (b) The reward probability for each second-stage choice is determined by a random walk drift. (c) An example of a trial sequence in the two-step task.
Author response image 1
Tables
Table 1
Simulation specification for Study 1.
| Model | Hybrid | Habit | K-DH |
|---|---|---|---|
| Parameter range | |||
| # agents | 100 | 100 | 100 |
| # trials | 200 | 200 | 200 |
| # blocks | 3 | 3 | 3 |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Using recurrent neural network to estimate irreducible stochasticity in human choice behavior
eLife 13:RP90082.
https://doi.org/10.7554/eLife.90082.3
