Selective consolidation of learning and memory via recall-gated plasticity
- Zuckerman Mind Brain Behavior Institute, Columbia University, United States
Figures
Figure 1
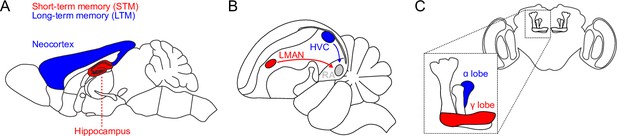
Schematic of short- and long-term memory systems across species and brain areas.
(A) In mice and other mammals, hippocampal memories are consolidated into neocortex. (B) Zebrafinch song learning initially depends on LMAN but later requires only HVC-to-RA synapses in the song motor pathway. (C) In the Drosophila mushroom body (inset), short- and long-term memories depend on dopamine-dependent plasticity in the γ and α lobes, respectively.
Figure 2 with 2 supplements
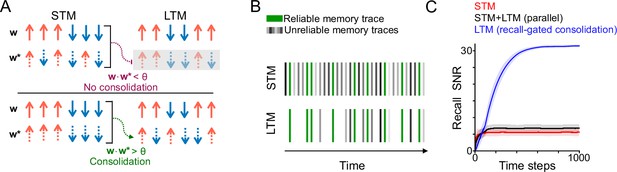
Recall-gated systems consolidation model.
(A) Schematic of systems consolidation model. Top and bottom rows illustrate different examples, in which a memory is not consolidated or consolidated, respectively. Memories correspond to patterns of candidate potentiation and depression events (dashed arrows) applied to a synaptic population with weights w (solid arrows). The synaptic population is divided into an STM (left) and LTM (right). Memories that provoke strong recall in the STM – that is, overlap strongly with the present synaptic state – enable plasticity (consolidation) in the LTM; otherwise plasticity in the LTM is gated (gray shaded rectangle). Note that the synaptic weights and the components of the memory corresponding to the LTM need not be linked to those of the STM (i.e. the patterns of arrows are different between the left and right columns). (B) Schematic of the environmental statistics. A reliable memory (green) arrives repeatedly with probability λ at each time step, with randomly sampled ‘unreliable’ memories (gray) interspersed. The LTM is exposed to a filtered subset of consolidated memory traces with a higher proportion of reliable memories. (C) Simulation of recall performance of a single reliable memory with time as it is presented with probability at each time step, N=2000 synapses (1000 each in the STM and LTM). The STM and LTM learning rates (binary switching probabilities) are p=0.25 and p=0.05, respectively, and the synaptic state is initialized randomly, each synapse initially active with probability 0.5. In the recall-gated model, the gating threshold is set at . Shaded regions indicate standard deviation across 1000 simulations.
Figure 2—figure supplement 1
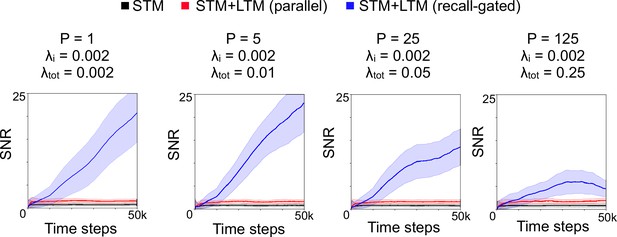
Same as Figure 2C, but with multiple reliable memories simultaneously learned, each recurring equally often at a rate for all reliable memories i.
Here synapses, and the STM and LTM learning rates are 0.05 and 0.01, respectively. In the recall-gated model, the gating threshold is set at . Each plot corresponds to a different number P of reliable memories being stored (the SNR shown is averaged across the reliable memories). The behavior of the SNR of an individual reliable memory is approximately the same as in the single-memory case for small values of λtot but diverges from it when λtot grows large.
Figure 2—figure supplement 2
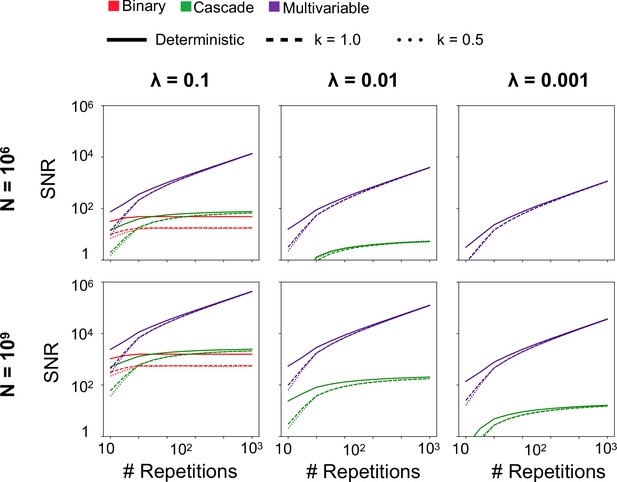
SNR as a function of repetitions for single populations without consolidation, varying the parameter k of the Weibull distribution governing interarrival times (and defining the learnable timescale in terms of the expected interarrival time).
The behavior of the systems scales similarly for diverse values of k, justifying the use of the deterministic approximation for theoretical calculations. The learning rate for the binary model here is set at 0.1.
Figure 3
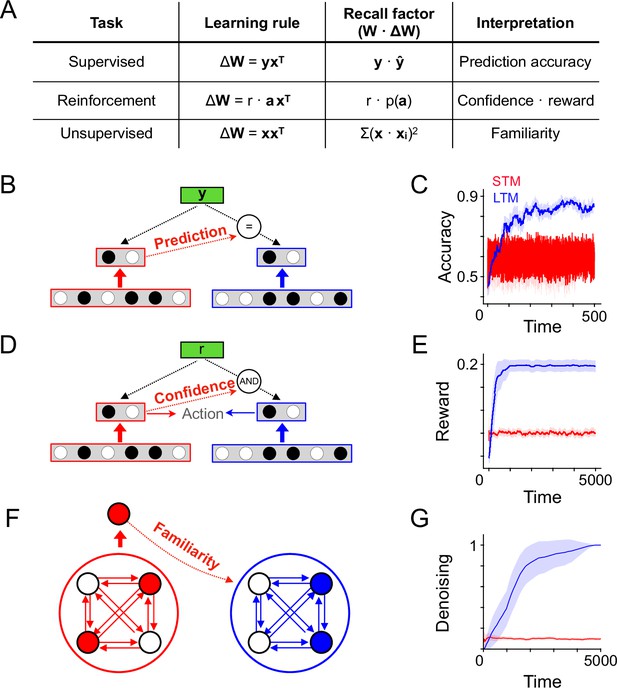
Circuit architectures for recall-gated consolidation model.
(A) Description of learning rules corresponding to different types of learning problems and corresponding expressions for the recall factor used in the recall-gated consolidation model. (B) Schematic indicating a possible implementation of the model in a supervised learning problem, where LTM plasticity is modulated by the consistency between STM predictions and ground-truth labels. (C) Like B, but for a reinforcement learning problem. LTM plasticity is gated by both STM action confidence and the presence of reward. (D) Like B and C, but for an autoassociative unsupervised learning problem. As above, corresponds to neural activity and to the network weights, which here are recurrent. LTM plasticity is gated by familiarity detection in the STM module. (E) Simulation of a binary classification problem, . There are 20 total stimuli each associated with a random binary (±1) label and each appearing with probability at each timestep (otherwise a random stimulus is presented, with a random binary label). Plot shows the classification accuracy over time, given by the outputs of the STM and LTM of the consolidation model. Shaded region indicates standard deviation over 50 simulations. (F) Simulation of a reinforcement learning problem, . There are five total stimuli, each appearing with probability at each timestep (otherwise a random stimulus is presented), and three possible actions. Each stimulus has a corresponding action that yields reward (the reward is randomly sampled for the random stimuli). The plot shows average reward per step over time, evaluated using the actions given by the STM or LTM (during learning, the STM action was always used). (G) Simulation of an autoassociative learning problem. . A single stimulus appears with probability at each timestep, and otherwise a random stimulus appears. Recall performance is evaluated by exposing the system to a noisy version of the reliable stimulus seen during training, allowing the recurrent dynamics of the network to run for 5 timesteps, and measuring the correlation of the final state of the network with the ground-truth pattern.
Figure 4 with 4 supplements
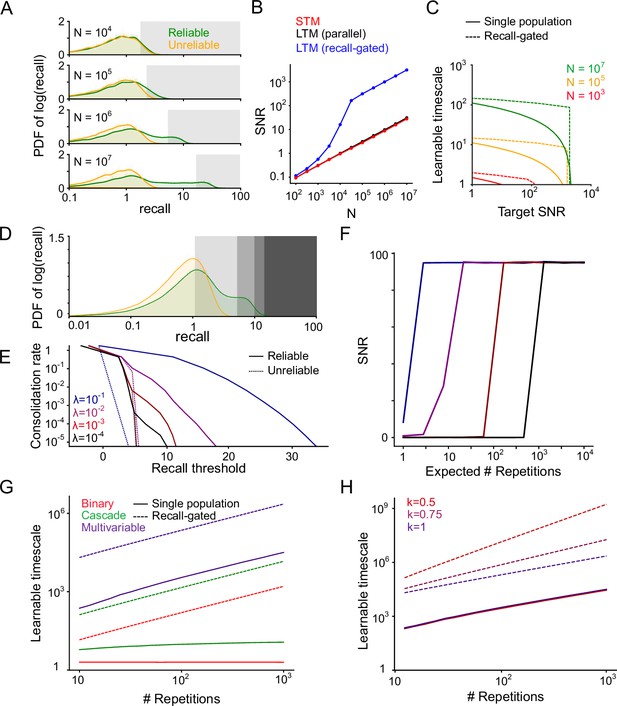
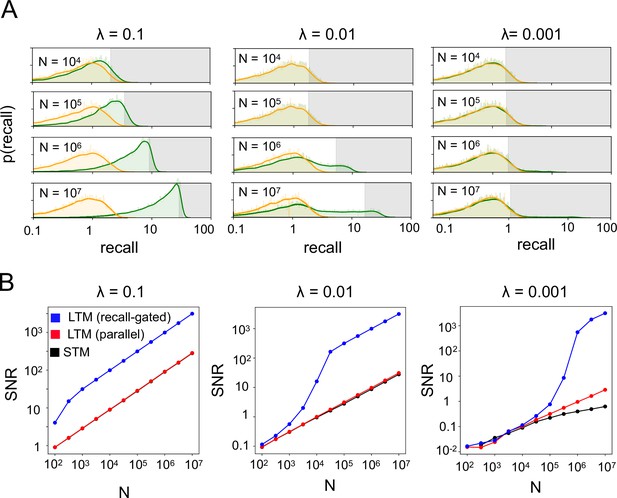
Properties of the recall-gated consolidation model.
(A) Distribution (probability density function) of reliable and unreliable memory overlaps (on a log scale), varying the number of synapses N, Shaded regions indicate consolidation thresholds that preserve 10% of reliable memory presentations. Units are standard deviations of the distribution of recall for randomly sampled memories. (B) LTM SNR induced by consolidation (with threshold set as in A, to consolidate 10% of reliable memory presentations) as N varies. The parallel model uses aslower learning rate (the value of p in the binary switching synapse model is a factor of 10 smaller) in the LTM than the STM. (C) Learnable timescale as a function of target SNR, for several values of N, using the binary switching synapse model with . (D) Distribution of reliable and unreliable memory overlaps, with various potential gating thresholds indicated, . (E) Fraction of memory presentations consolidated (log scale) vs recall threshold for consolidation, . (F) LTM SNR induced by consolidation vs. the expected number of repetitions before consolidation occurs, , same color legend as panel E. Increasing the expected number of repetitions corresponds to setting a more stringent consolidation threshold which filters a higher proportion of reliable memory presentations. (G) Learnable timescale at a target SNR of 10 as a function of number of reliable memory repetitions for several underlying synapse models, . (H) Same as G, considering only the multivariable model as the underlying synapse model, and varying the interarrival interval regularity factor k.
Figure 4—figure supplement 1
Effects of varying rate of reliable memory presentations.
Figure 4—figure supplement 2
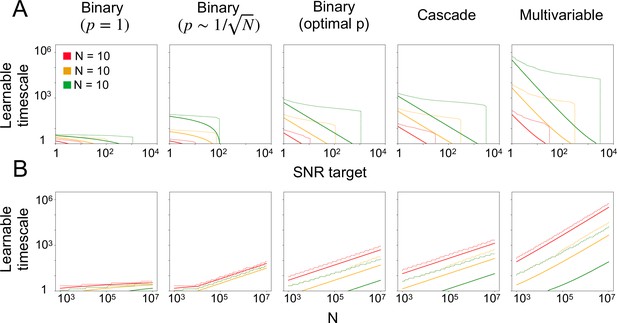
Comparison of different synaptic learning rules.
(A) Same as Figure 4C, also varying the underlying synaptic learning rule. (B) Same learnable timescale information as panel A, presented as a function of the synaptic population size N.
Figure 4—figure supplement 3
Same information as Figure 4G, varying the population size N and the desired SNR.
Figure 4—figure supplement 4
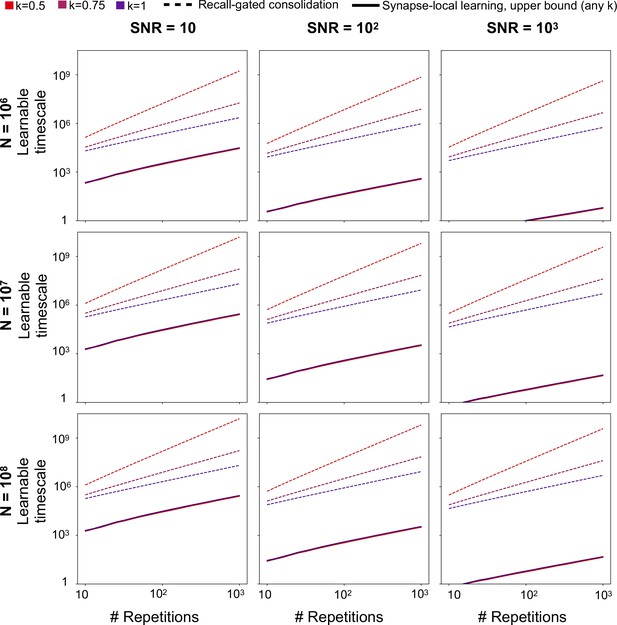
Same information as Figure 4H, varying the population size N and the desired SNR.
Figure 5 with 3 supplements
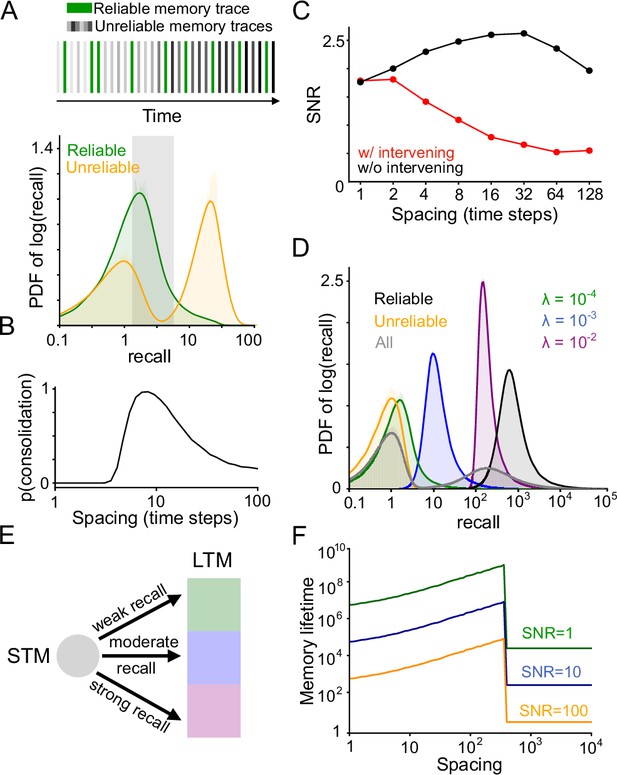
Alternative memory gating functions.
(A) Top: Example sequence of memory presentations where unreliable memories (gray) can repeat multiple times, but only within within a short timescale (note gradient of light to dark). Bottom: Distribution of reliable and unreliable memory overlaps induced by such memory presentation statistics (log scale on x axis). Shaded region indicates overlap values that are at least ten times as likely for reliable memories as for unreliable memories. (B) Probability of consolidation, with the gating function chosen such that only overlaps within the shaded region of panel A are consolidated, as a function of interarrival interval. (C) SNR at 8 timesteps following 5 spaced repetitions of a memory, with spacing interval indicated on the x axis, for the multivariable synapse model of Benna and Fusi, 2016 with no systems consolidation. Spaced training effects are present at short timescales, but not if other memories are presented during the interpresentation intervals. (D) Distribution of recall strengths corresponding to different kinds of memories, in an environment with many reliable memories. In the environment model, reliable memories are reinforced with different interarrival interval distributions, and the timescales of these distributions for different memories are distributed log-uniformly. The environment also has as a background rate of unreliable memory presentations appearing at fraction 0.9 of timesteps. (E) Depiction of a generalization of the model in which memories can be consolidated into different LTM sub-modules, according to gating functions tuned to different recall strengths (intended to target reliable memories with different timescales of recurrence). (F) A consequence of the model outlined in panel E is a smooth positive dependence of memory lifetime on the spacing of repetitions, up to some threshold spacing.
Figure 5—figure supplement 1
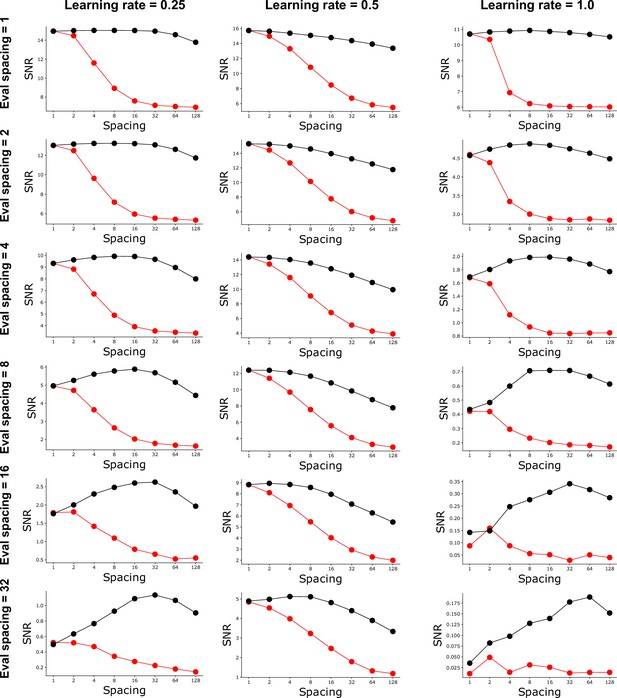
Same information as Figure 5C, varying the learning rate (scale of potentiation/depression impulses, relative to the maximum/minimum threshold values in the model of Benna and Fusi, 2016), and the length of time following spaced training at which the system’s recall SNR is evaluated.
Figure 5—figure supplement 2
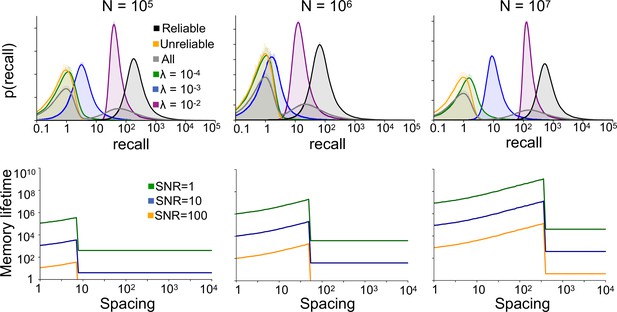
Same as Figure 5D (top row) and Figure 5F (bottom row), for different population sizes N.
Figure 5—figure supplement 3
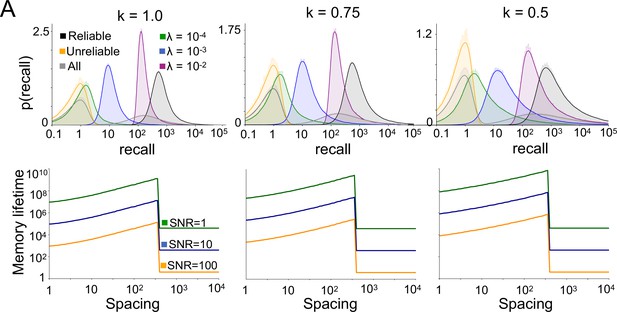
Same as Figure 5D (top row) and Figure 5F (bottom row), for different memory recurrence regularity factors (Weibull distribution parameter k).
Figure 6
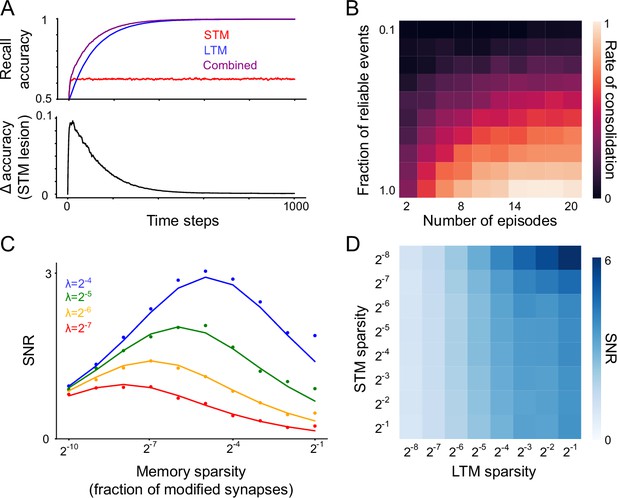
Predictions of the model.
(A) Top: Recall performance for a single reliable memory (true positive rate, with a decision threshold set to yield a 10% false positive rate) as learning progresses. Simulation environment is the same as in Figure 2C. . Bottom: difference between combined recall performance and LTM-only performance. The STM makes diminishing contributions to recall over time. (B) Probability of consolidation into LTM increases with experience and with the reliability of the environment (parameterized here by the recurrence frequency λ of reliable memories). Simulation environment is the same as in panel A. (C) For a single population of binary synapses (no consolidation) and Poisson memory recurrence, mean SNR as a function of reliable memory recurrence frequency λ and memory sparsity f. Dots indicate simulation results and solid lines indicate analytical approximation. N=1,024. (D) For the systems consolidation model using binary synapses, total system SNR (N=256) as a function of memory sparsity in the STM and LTM.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Selective consolidation of learning and memory via recall-gated plasticity
eLife 12:RP90793.
https://doi.org/10.7554/eLife.90793.3
