Serial attentional resource allocation during parallel feature value tracking
- Department of Neurology, Otto-von-Guericke University, Germany
- Department of Behavioral Neurology, Leibnitz Institute for Neurobiology, Germany
- Kliniken Schmieder, Germany
Figures
Figure 1
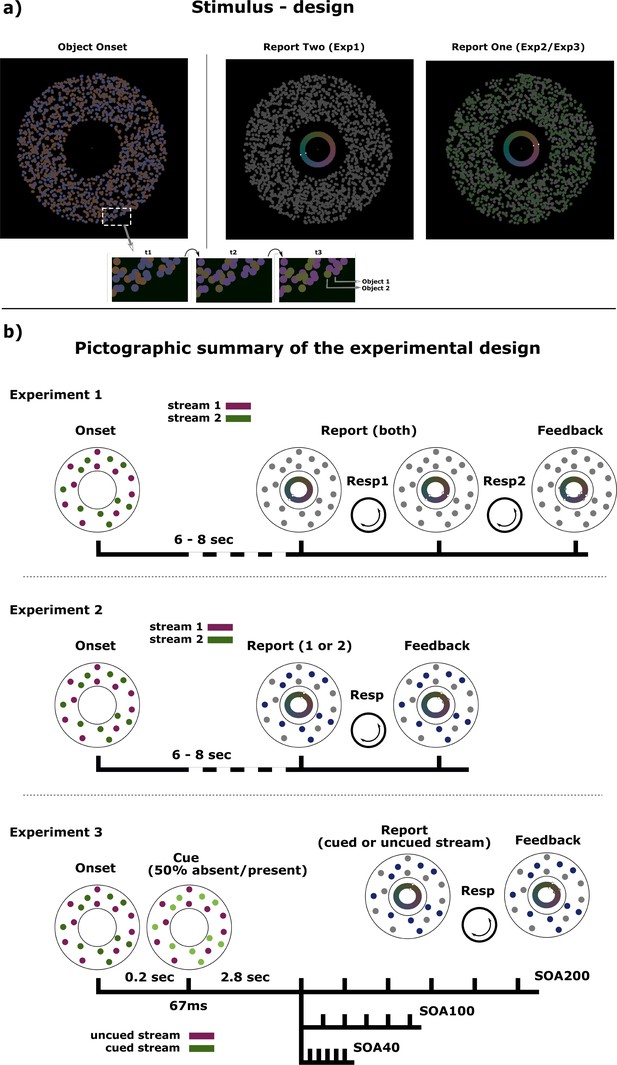
Experimental paradigm.
(a) General stimulus design: Two superimposed dot clouds are present throughout each trial. Subjects are asked to attend to the colors of both objects as they transit through hue-space. In order to remove any spatial depth cue specific to one of the two objects, individual dots are superimposed randomly at time of initial generation. Furthermore, 10 random dots of each objects interchange identity (current color) at each frame throughout the trial, thus discouraging the generation of any spatial configuration in aiding feature tracking. At the end of the tracking phase one (Exp2/Exp3) or two (Exp1) of the streams change to grey and subjects have to report the last perceived color for that object using a dial. (b) Experimental design and time-course of trials for all three experiments. In experiment 1 and 2, subjects are tracking both color streams for 6–8 sec after which they are asked to report back on one (Exp1) or two (Exp2) of the streams. Probed color streams turn grey to indicate that they have to be reported on. After dialing in the response with a cursor on a centrally presented color wheel, subjects receive feedback about the correct response via a second cursor on the same color wheel. Experiment 3 additionally introduces a luminance cue for one of the two streams at the beginning of the tracking phase in 50% of the trials. After a set of fixed tracking intervals, subjects have to report on the color of the previously cued or uncued stream. This experiment is performed with three different sets (SOA200/SOA100/SOA40) of six tracking intervals.
Figure 2
Aquisition of precision responses per trial and mixture modeling.
(a) In experiment 1, subjects have to report on two target colors in sequence. The two reports (R1 and R2) and the two target colors (Ta and Tb) for one trial create two possible target-response associations (and therefore two pairs of precision responses): (Ta-R1 & Tb-R2) or (Tb-R1 & Ta-R2). This ambiguity was resolved by pairing targets and responses based on the minimum angular difference for the first response to one of the targets (Min(Tx-R1)), and the second response to the remaining target (T~x-R2). This pairing is based on the assumption, that the first response would always be performed with higher confidence by the subject. It would be highly unlikely that for one trial subjects’ first response would be a guess and the second response an accurate report based on correct tracking if they were able to only track one stream. Additionally, this leaves the possibility of the second response still being more accurate than the first response (by chance or actual cognitive performance). (b) Von Mises mixture model utilized in the experiments. The distribution of all precision responses (angular differences between response and target) would be the sum of responding each of the two tracked streams with each being allocated a certain cognitive resource (high/low precision). (c) The results of the Von Mises mixture models (as the pair of precision responses) is tested by Monte-Carlo-simulations. We tested, whether the parameters of the Von Mises mixture models can be estimated in artificially simulated sets of high and low precision target-response distributions based on those same parameters. The simulations confirm, that the estimated parameters reflect the ground truth of a sum of two precision distributions and not just a general inherent property of the model.
Figure 3
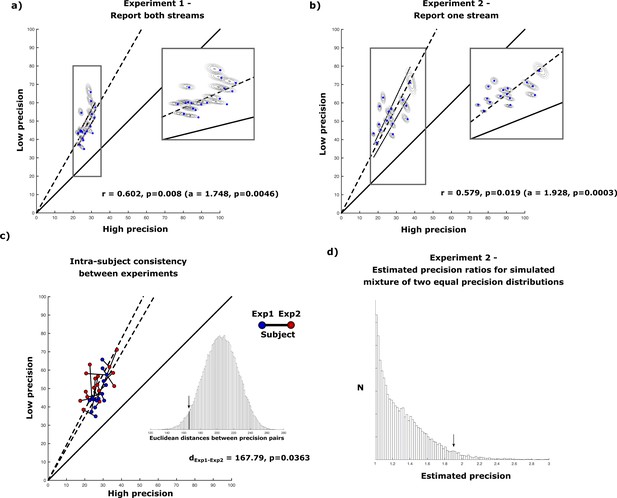
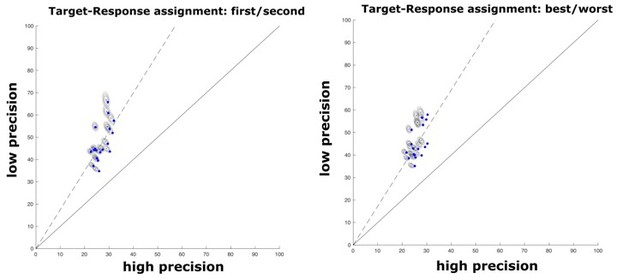
Results of uneven attentional resource distribution amongst two parallel color streams in experiment 1 and 2.
(a) High and low precision estimates for each of the tested subjects (n = 18) (blue dots) in experiment 1. Additionally, the results of the Monte-Carlo simulated precision estimates for each subject are displayed as two-dimensional gaussians. In general, subjects are almost twice as precise in responding to one of the streams compared to the other stream. (b) Results for experiment 2. When subjects (n = 16) have to report only one stream per trial (while still attending to both color streams), the general ratio of high and low precision responses remain. (c) The same subjects show very similar pairs of precision estimates in both experiments (irrespective of whether they have to respond to both streams sequentially or only one stream). (d) Estimated precision estimates for mixture models containing two distributions with equal deviation based on the means of each subjects estimated precisions. The estimated precision ratio of Mixture models containing two equal distributions reaches a median ratio of 1.24 and values higher than 1.928 in less than 5% of conducted simulations.
Figure 4
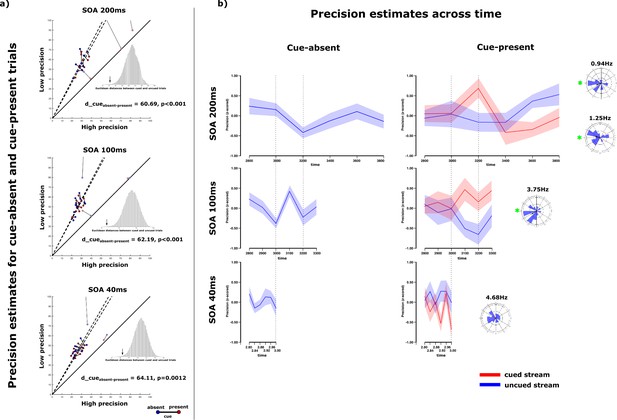
Results of Experiment 3.
(a) The ratio of slightly lower than 2 remains present between high and low precision estimates for experiment 3. Importantly, individual precision estimates do not vary between trials in which a luminance cue is presented and in trials in which the luminance change is absent. The cue itself does not influence the general precision estimate collapsed over tracking intervals. This holds true for all three sets of tracking intervals (SOA200 /SOA100/SOA40). (b) Precision estimate time courses with standard errors (n = 15). For cue-absent trials no systematic variation in precision estimates could be observed over time in Exp3a (SOA200) and Exp3c (SOA100). However, precision estimates changed for different tracking intervals in cue-absent trials in Exp3b (SOA100). In Exp3a (SOA200), precision estimates for the cued and uncued stream differed over time. Specifically, precision for both streams seemed to exhibit an antiphasic relation at around 1Hz. Phase differences of precision estimates between cued and uncued streams cluster around 180° in this case. Exp3b (SOA100) shows a very similar time-course for the precision estimates of cued and uncued streams over 2.8 sec to 3.2 sec comparable to the SOA200-experiment. Another, faster, oscillation (3.75Hz) can be additionally observed with the same anti-phasic relation between cued and uncued stream. In Exp3c (SOA40) no stream-related differences over the tested intervals can be observed.
Author response image 1
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Serial attentional resource allocation during parallel feature value tracking
eLife 12:e91183.
https://doi.org/10.7554/eLife.91183
