Novel cyclic homogeneous oscillation detection method for high accuracy and specific characterization of neural dynamics
- Department of Neurosurgery, Washington University School of Medicine, United States
- National Center for Adaptive Neurotechnologies, United States
Figures
Figure 1
Examples of non-sinusoidal and sinusoidal neural oscillations recorded from the human auditory cortex.
Detecting the presence, onset/offset, and fundamental frequency of non-sinusoidal oscillations is challenging. This is because the power spectrum of the non-sinusoidal theta-band oscillation (A) exhibits multiple harmonic peaks in the alpha and beta bands (B). The peaks of these harmonics are also exhibited in the time-frequency domain (C). To determine whether these peaks are independent oscillations or harmonics of the fundamental frequency, we tested whether fundamental theta oscillation and potential beta-band harmonic oscillations exhibit a 1:3 phase-locking (D–F), i.e., whether the beta-band oscillation is a true third harmonic of the fundamental theta-band oscillation. In our test, we found that the theta-band oscillation was significantly phase-locked to the beta-band oscillation with a 1:3 ratio in their frequencies (F, number of permutation = 300, p<0.001). This means that the tested theta- and beta-band oscillations are part of one single non-sinusoidal neural oscillation. We applied the same statistical test to a more sinusoidal neural oscillation (G). Since this neural oscillation more closely resembles a sinusoidal shape, it does not exhibit any prominent harmonic peaks in the alpha and beta bands within the power spectrum (H) and time-frequency domain (I). Consequently, our test found that the phase of the theta-band and beta-band oscillations were not phase-locked (J–L). Thus, this statistical test suggests the absence of a harmonic structure.
Figure 2
Using autocorrelation to determine the fundamental frequency of non-sinusoidal and sinusoidal neural oscillations recorded from the human auditory cortex.
(A) Temporal dynamics of non-sinusoidal and (B) sinusoidal neural oscillation and (C, D) their autocorrelation. The periodicity of peaks in the autocorrelation reveals the fundamental frequency of the underlying oscillation. Asymmetry in peaks and troughs of the autocorrelation is indicative of a non-sinusoidal oscillation.
Figure 3
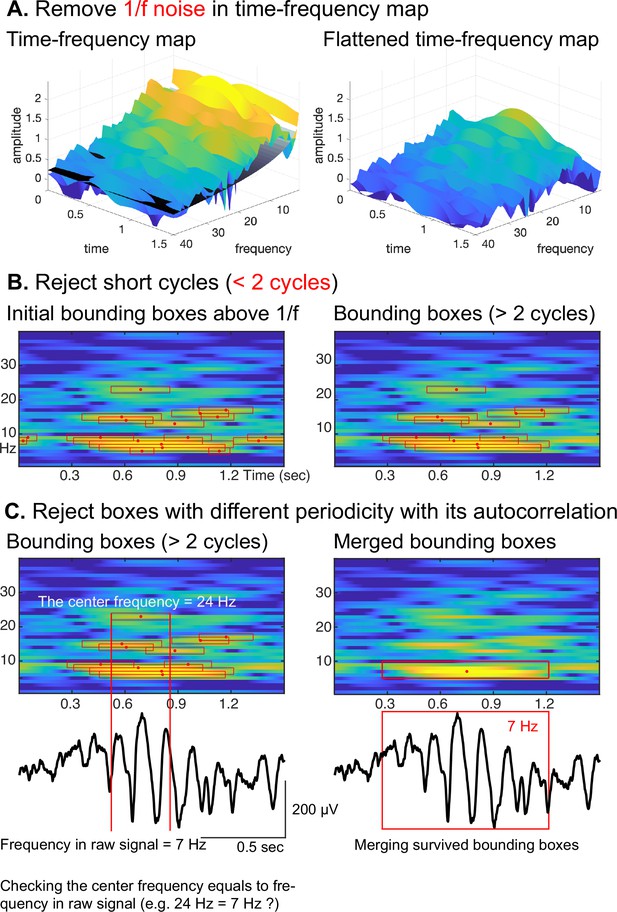
Procedural steps of cyclic homogeneous oscillation (CHO).
(A) First, to identify periodic oscillations, CHO removes the underlying 1/f aperiodic noise in the time-frequency space and generates initial bounding boxes of candidate oscillations. (B) In the second step, CHO rejects bounding boxes that exhibit less than 2 oscillatory cycles. (C) In the final step, CHO limits the analysis to only those bounding boxes that exhibit the same frequency in the time-frequency map and autocorrelation. Each remaining bounding box is characterized by onset/offset, frequency range, center frequency, and number of cycles.
Figure 4 with 2 supplements
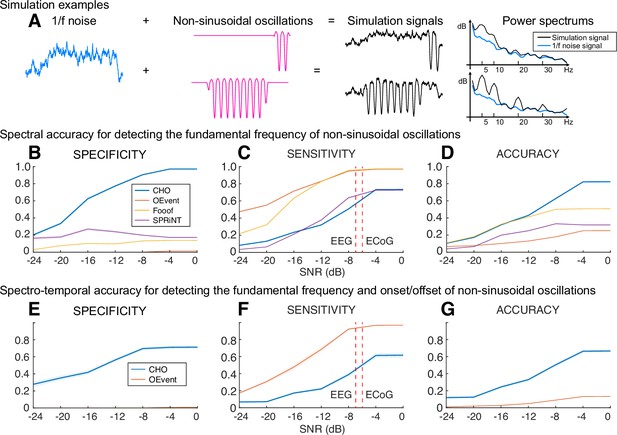
Performance of cyclic homogeneous oscillation (CHO) in detecting synthetic non-sinusoidal oscillations.
(A) We evaluated CHO by verifying its specificity, sensitivity, and accuracy in detecting the fundamental frequency of non-sinusoidal oscillatory bursts (2.5 cycles, 1–3 s long) convolved with 1/f noise. (B–D) CHO outperformed existing methods in detecting the fundamental frequency of non-sinusoidal oscillation (FOOOF: fitting of oscillations using 1/f Donoghue et al., 2020, oscillation event (OEvent) Neymotin et al., 2022: Oscillation event detection method, and SPRiNT Wilson et al., 2022: Spectral Parameterization Resolved in Time) in specificity and accuracy, but not in sensitivity. CHO exhibited fewer false-positive and more true-negative detections than existing methods. (C) However, at signal-to-noise ratio (SNR) levels of alpha oscillations found in electroencephalographic (EEG) and electrocorticographic (ECoG) recordings (i.e. –7 and –6 dB, respectively), the sensitivity of CHO in detecting the peak frequency of non-sinusoidal oscillation is comparable to that of SPRiNT. (D) This means that the overall accuracy of CHO was higher than that of existing methods. (E–G) CHO outperformed existing methods in detecting the fundamental frequency and onset/offset of non-sinusoidal oscillation. (F) Similar to the results shown in (C) CHO can effectively detect the fundamental frequency and onset/offset for more than half of all oscillations at SNR levels of alpha oscillations found in EEG and ECoG recordings.
Figure 4—figure supplement 1
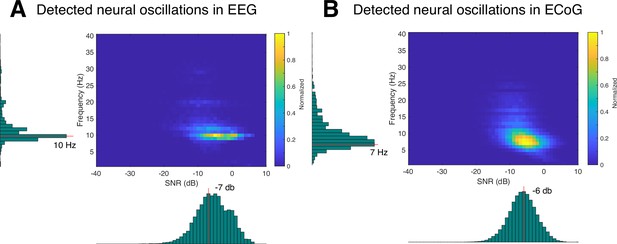
Signal-to-noise ratio (SNR) histograms of (A) electroencephalography (EEG) and (B) electrocorticography (ECoG).
Figure 4—figure supplement 2
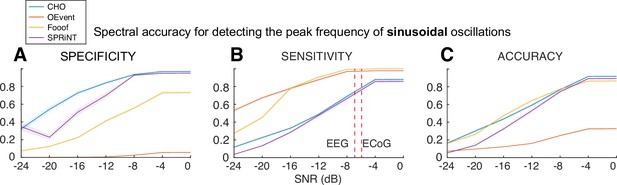
Synthetic sinusoidal oscillations.
We evaluated CHO by verifying its specificity (A), sensitivity (B), and accuracy (C) in detecting the fundamental frequency of sinusoidal oscillatory bursts (2.5 cycles, 1–3 seconds long) convolved with 1/f noise.
Figure 5 with 1 supplement
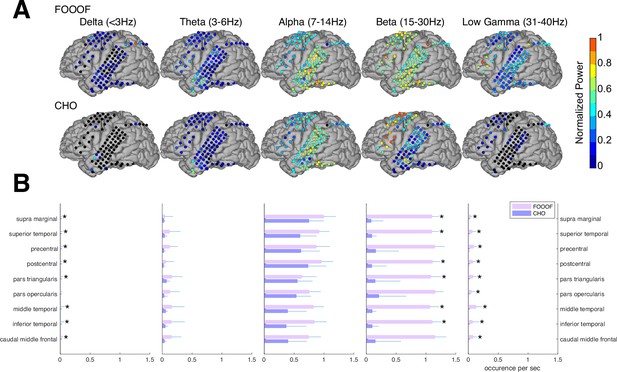
Validation of cyclic homogeneous oscillation (CHO) in detecting oscillations in electrocorticographic (ECoG) signals.
(A) We applied CHO and fitting of oscillations using 1/f (FOOOF) to determine the fundamental frequency of oscillations from ECoG signals recorded during the pre-stimulus period of an auditory reaction-time task. FOOOF detected oscillations primarily in the alpha- and beta-band over STG and pre-motor area. In contrast, CHO also detected alpha-band oscillations primarily within STG, and more focal beta-band oscillations over the pre-motor area, but not STG. (B) We investigated the occurrence of each oscillation within defined cerebral regions across eight ECoG subjects. The horizontal bars and horizontal lines represent the median and median absolute deviation (MAD) of oscillations occurring across the eight subjects. An asterisk (*) indicates statistically significant differences in oscillation detection between CHO and FOOOF (Wilcoxon rank-sum test, n=8, p<0.05 after Bonferroni correction).
Figure 5—figure supplement 1
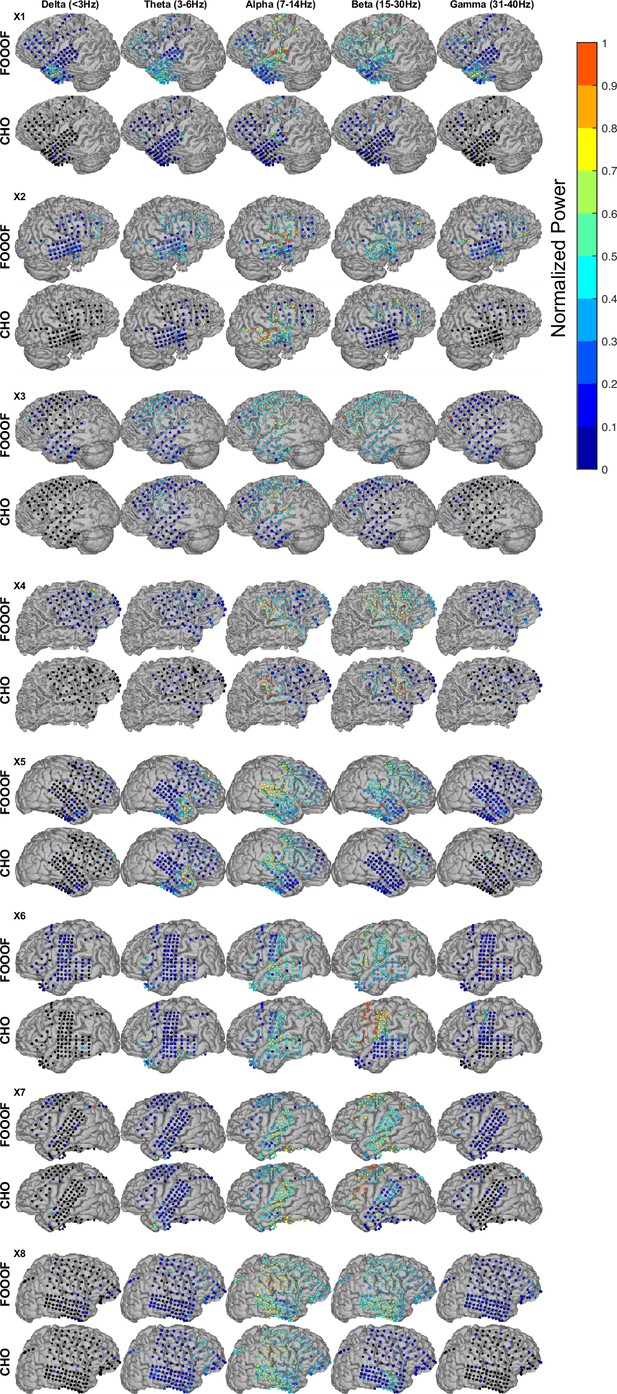
Electrocorticographic (ECoG) results using fitting of oscillations using 1/f (FOOOF) and cyclic homogeneous oscillation (CHO) for all subjects.
Figure 6 with 1 supplement
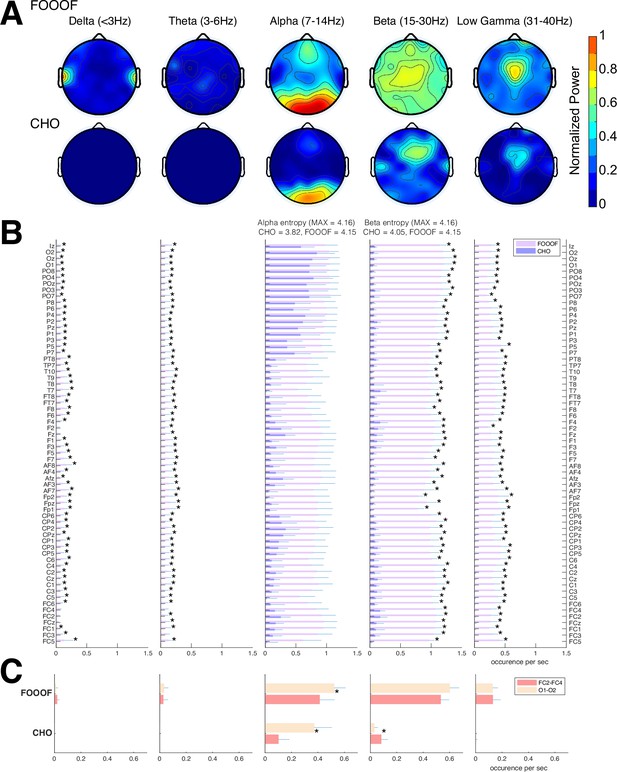
Validation of cyclic homogeneous oscillation (CHO) in detecting oscillations in electroencephalographic (EEG) signals.
(A) We applied CHO and fitting of oscillations using 1/f (FOOOF) to determine the fundamental frequency of oscillations from EEG signals recorded during the pre-stimulus period of an auditory reaction-time task. FOOOF primarily detected alpha-band oscillations over frontal/visual areas and beta-band oscillations across all areas (with a focus on central areas). In contrast, CHO detected alpha-band oscillations primarily within visual areas and detected more focal beta-band oscillations over the pre-motor area, similar to the electrocorticographic (ECoG) results shown in Figure 5. (B) We investigated the occurrence of each oscillation within the EEG signals across seven subjects. An asterisk (*) indicates statistically significant differences in oscillation detection between CHO and FOOOF (Wilcoxon rank-sum test, n=7, p<0.05 after Bonferroni correction). CHO exhibited lower entropy values of alpha and beta occurrence than FOOOF across 64 channels. (C) We compared the performance of FOOOF and CHO in detecting oscillation across visual and pre-motor-related EEG channels. CHO detected more alpha and beta oscillations in visual cortex than in pre-motor cortex. FOOOF detected alpha and beta oscillations in visual cortex than in pre-motor cortex.
Figure 6—figure supplement 1
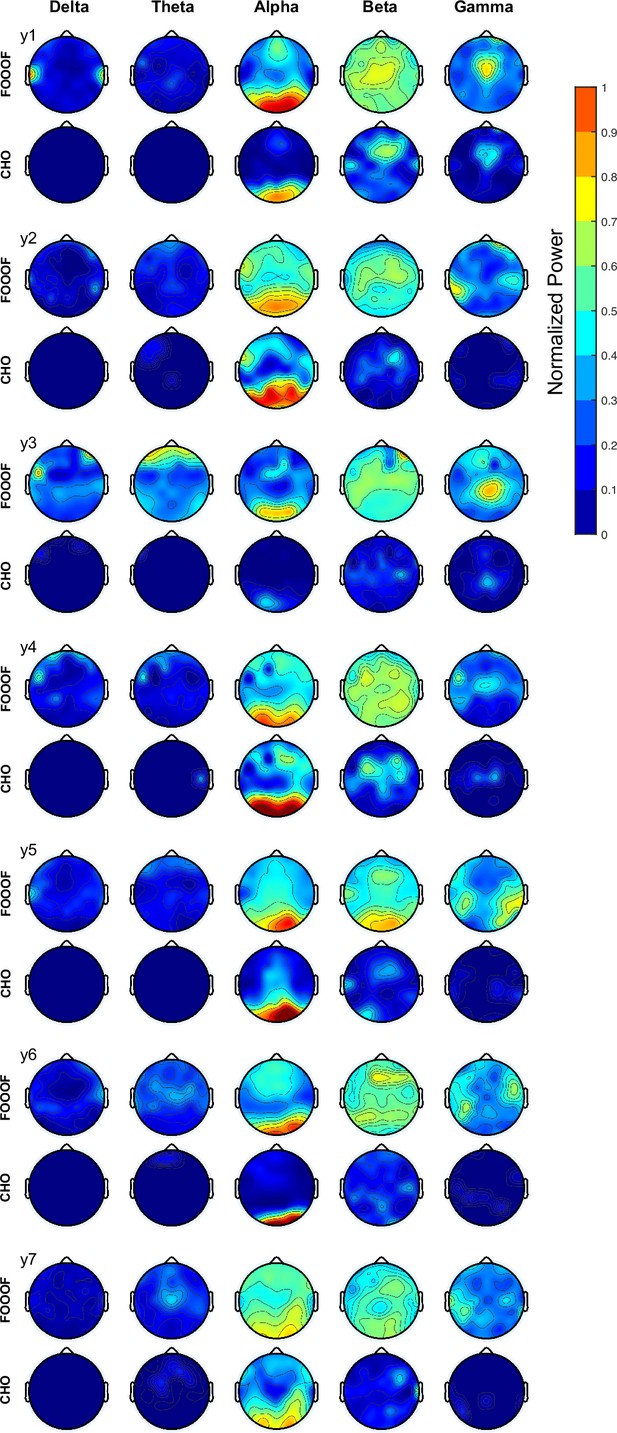
All electroencephalographic (EEG) results using fitting of oscillations using 1/f (FOOOF) and cyclic homogeneous oscillation (CHO).
Figure 7
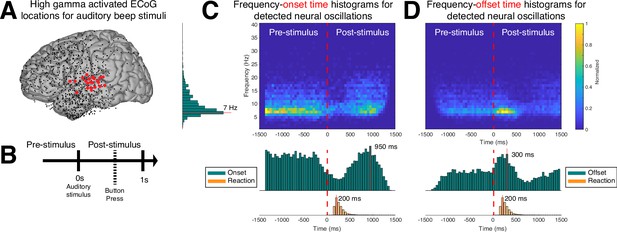
Application of cyclic homogeneous oscillation (CHO) in determining the spatiotemporal characteristics of neural oscillations in electrocorticographic (ECoG) signals during a reaction-time task.
(A) We selected those cortical locations (red) from all locations (black) that exhibited a significant broadband gamma response to an auditory stimulus in a reaction-time task. (B) In this task, the subjects were asked to react as fast as possible with a button press to a salient auditory stimulus. (C–D) Onset and offset times of detected neural oscillations. Fundamental oscillations were centered around 7 Hz (left histogram). Onset and offset times during pre-stimulus period exhibited a uniform distribution, indicating that 7 Hz oscillations randomly started and stopped during this period. A trough in the onset and a peak in the offset of 7 Hz oscillations is visible from the histograms, indicating a general decrease of the presence of neural oscillations immediately following the auditory stimulus. The subjects responded with a button press within 200 ms of the auditory stimulus, on average. The prominent peak in the offset and onset of oscillations at 300 and 950 ms post-stimulus, respectively, indicates a suspension of oscillations in response to the auditory stimulus, and their reemergence after the execution of the button press behavior.
Figure 8 with 1 supplement
Application of cyclic homogeneous oscillation (CHO) in determining the fundamental frequency and duration of hippocampal oscillations in stereoelectroencephalographic (SEEG) signals during resting state.
(A) We recorded hippocampal oscillations from one representative human subject implanted with SEEG electrodes within the left anterior hippocampus. (B) Power spectrum (blue) and 1/f trend (red) for one electrode within the anterior-medial left hippocampus (red dot in A). The power spectrum of a 10-s-long hippocampal signal indicates the presence of neural activity over a 1/f trend across a wide frequency band up to 30 Hz. (C) In marked contrast to the relatively unspecific results indicated by the power spectrum, CHO detected several distinct hippocampal fast theta bursts. (D) This detection is based on first denoising the power spectrum using 1/f fitting (principle criterion #1 of CHO), which yields initial bounding boxes that include short-cycled oscillations and harmonics. (E) The autocorrelation step then successfully removes all short-cycled oscillations and harmonics, with only those bounding boxes remaining that exhibit a fundamental frequency.
Figure 8—figure supplement 1
All results from six stereoelectroencephalographic (SEEG) subjects using the fitting of oscillations using 1/f (FOOOF) and cyclic homogeneous oscillation (CHO) methods.
Figure 9
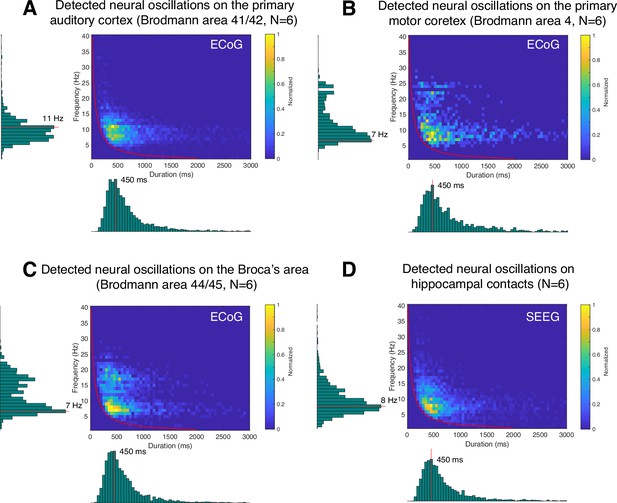
Application of cyclic homogeneous oscillation (CHO) in determining the fundamental frequency and duration of neural oscillations in auditory cortex, motor cortex, Broca’s area, and hippocampus during resting state.
This figure presents the distribution of detected oscillations in a two-dimensional frequency/duration histogram and projected onto frequency and duration axes. The red line indicates the rejection line (less than 2 cycles). (A) In primary auditory cortex (Brodmann area 41/42), the most dominant frequency and duration in the auditory cortex was 11 Hz with 450 ms duration. (B) The primary motor cortex’s most dominant frequency was 7 Hz with 450 ms duration, but more beta rhythms were detected with >500 ms duration than in auditory cortex. (C) Broca’s area exhibits similar characteristics to that of motor cortex, but dominant beta-band oscillations were found to be less present than in motor cortex. (D) Hippocampus primarily exhibits 8 Hz oscillations with 450 ms duration.
Author response image 1
Algorithm 1.
Author response image 2
Figure 5-supplementary figure 1.
Author response image 3
Figure 5-supplementary figure 1.
Author response image 4
Figure 8-supplementary figure 1.
Author response image 5
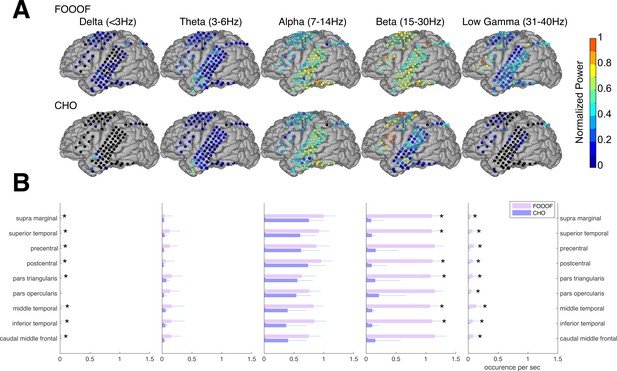
Validation of CHO in detecting oscillations in ECoG signals.
A. We applied CHO and FOOOF to determine the fundamental frequency of oscillations from ECoG signals recorded during the pre-stimulus period of an auditory reaction time task. FOOOF detected oscillations primarily in the alpha- and beta-band over STG and pre-motor area. In contrast, CHO also detected alpha-band oscillations primarily within STG, and more focal beta-band oscillations over the pre-motor area, but not STG. B. We investigated the occurrence of each oscillation within defined cerebral regions across eight ECoG subjects. The horizontal bars and horizontal lines represent the median and median absolute deviation (MAD) of oscillations occurring across the eight subjects. An asterisk (*) indicates statistically significant differences in oscillation detection between CHO and FOOOF (Wilcoxon rank-sum test, p<0.05 after Bonferroni correction).”
Author response image 6
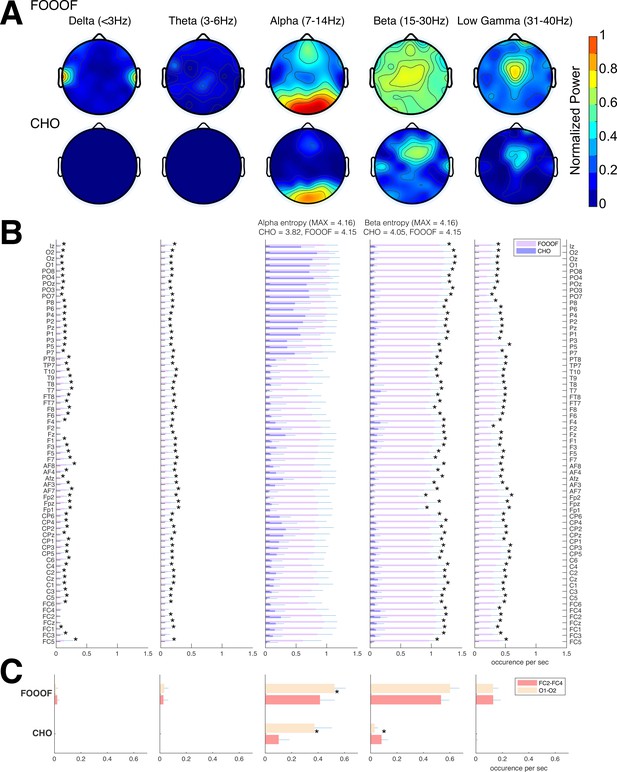
Validation of CHO in detecting oscillations in EEG signals.
A. We applied CHO and FOOOF to determine the fundamental frequency of oscillations from EEG signals recorded during the pre-stimulus period of an auditory reaction time task. FOOOF primarily detected alpha-band oscillations over frontal/visual areas and beta-band oscillations across all areas (with a focus on central areas). In contrast, CHO detected alpha-band oscillations primarily within visual areas and detected more focal beta-band oscillations over the pre-motor area, similar to the ECoG results shown in Figure 5. B. We investigated the occurrence of each oscillation within the EEG signals across seven subjects. An asterisk (*) indicates statistically significant differences in oscillation detection between CHO and FOOOF (Wilcoxon rank-sum test, p<0.05 after Bonferroni correction). CHO exhibited lower entropy values of alpha and beta occurrence than FOOOF across 64 channels. C. We compared the performance of FOOO and CHO in detecting oscillation across visual and pre-motor-related EEG channels. CHO detected more alpha and beta oscillations in visual cortex than in pre-motor cortex. FOOOF detected alpha and beta oscillations in visual cortex than in pre-motor cortex.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Novel cyclic homogeneous oscillation detection method for high accuracy and specific characterization of neural dynamics
eLife 12:RP91605.
https://doi.org/10.7554/eLife.91605.3
