Research Article

Physics of Living Systems

The exchange dynamics of biomolecular condensates

Center for the Physics of Biological Function, Princeton University, United States
Department of Physics and Astronomy, Johns Hopkins University, United States
Department of Biophysics, Johns Hopkins University, United States
Department of Physics, Princeton University, United States
Department of Chemical and Biological Engineering, Princeton University, United States
Howard Hughes Medical Institute, United States
Department of Mechanical and Aerospace Engineering, Princeton University, United States
Department of Molecular Biology, Princeton University, United States
Lewis-Sigler Institute for Integrative Genomics, United States

Sep 25, 2024

https://doi.org/10.7554/eLife.91680.3

Open access
Copyright information

Figures
Additional files

11 figures and 2 additional files

Figures

Figure 1

Download asset Open asset

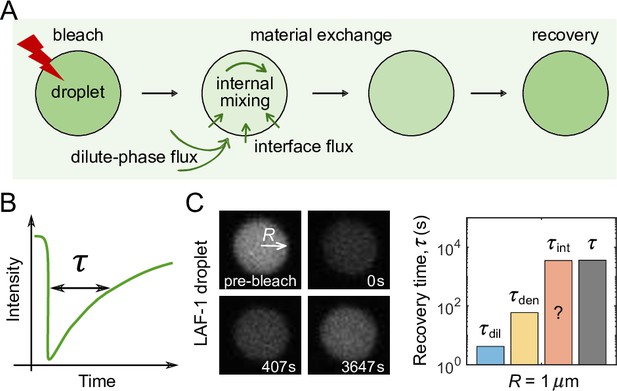
FRAP experiments on droplets.

(A) Schematic of a FRAP experiment in which an entire droplet is photobleached and the recovery of fluorescence is recorded. Material exchange between the condensate and the surrounding dilute phase can be limited by the flux of unbleached molecules coming from the dilute phase, the speed of internal mixing in the dense phase, or the flux passing through the interface. (B) The recovery time $τ$ is defined as the time required for fluorescence to return 63% (i.e. $1 - 1 / e$ ) of the way back to its original level. (C) Experimental data from Taylor et al., 2019 in which a LAF-1 droplet of radius $R = 1 µm$ recovers from photobleaching. (Left) Images before bleaching, immediately after bleaching of the entire droplet region, and at two subsequent times. (Right) Expected recovery times $τ_{dil} = c_{den} R^{2} / (3 c_{dil} D_{dil}) = 4.2 \pm 3.2 s$ and $τ_{den} = R^{2} / (π^{2} D_{den}) = 60 \pm 18 s$ if the slowest recovery process was either the flux from the dilute phase or diffusion within the droplet, respectively, with $D_{den} = 0.0017 \pm 0.0005 µ m^{2} / s$ , $D_{dil} = 94 \pm 11 µ m^{2} / s$ , and $c_{den} / c_{dil} = 1190 \pm 880$ taken from Taylor et al., 2019. While the timescale associated with interface resistance $τ_{int}$ is unknown, the measured recovery time $τ = 4570 \pm 470 s$ is much longer than $τ_{dil}$ and $τ_{den}$ , suggesting the recovery is limited by flux through the interface, with an interface conductance of $κ = R / 3 / (τ - τ_{dil} - τ_{den}) = (7.4 \pm 0.8) \times 10^{- 5} µ m / s$ .

Figure 2

Download asset Open asset

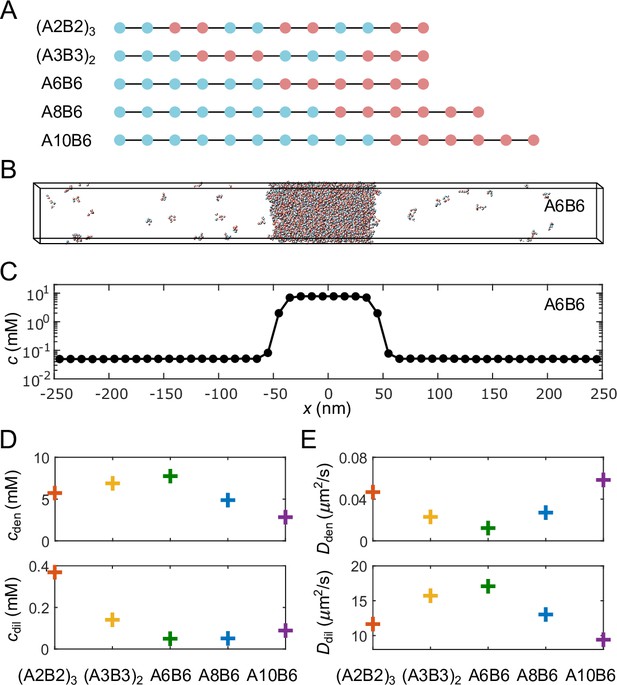
Coarse-grained molecular-dynamics simulations of multivalent phase-separating polymers.

(A) Each polymer is composed of monomers (‘stickers’) of type A (blue) or B (red), and modeled as a linear chain of spherical particles each with a diameter of 2 nm, connected by stretchable bonds with an equilibrium length of 3.9 nm. Stickers of different types have an attractive interaction, while stickers of the same type interact repulsively, ensuring one-to-one binding between the A and B stickers. (B) Snapshot of a simulation of 1000 A6B6 polymers in a 500 nm × 50 nm × 50 nm box with periodic boundary conditions. The system undergoes phase separation into a dense phase (middle region) and a dilute phase (two sides), driven by the one-to-one A-B bonds. (C) Polymer concentration profile for the simulation in (B) with the center of the dense phase aligned at $x = 0$ and averaged over time and over 10 simulation repeats. (D) Average total polymer concentrations in the dense (top) and dilute (bottom) phases from simulations of the five types of polymers shown in (A). (E) Polymer diffusion coefficients in the dense (top) and dilute (bottom) phases. All simulations were performed and snapshots were obtained using LAMMPS Plimpton, 1995. Please refer to Appendix 2 for simulation details.

Figure 3

Download asset Open asset

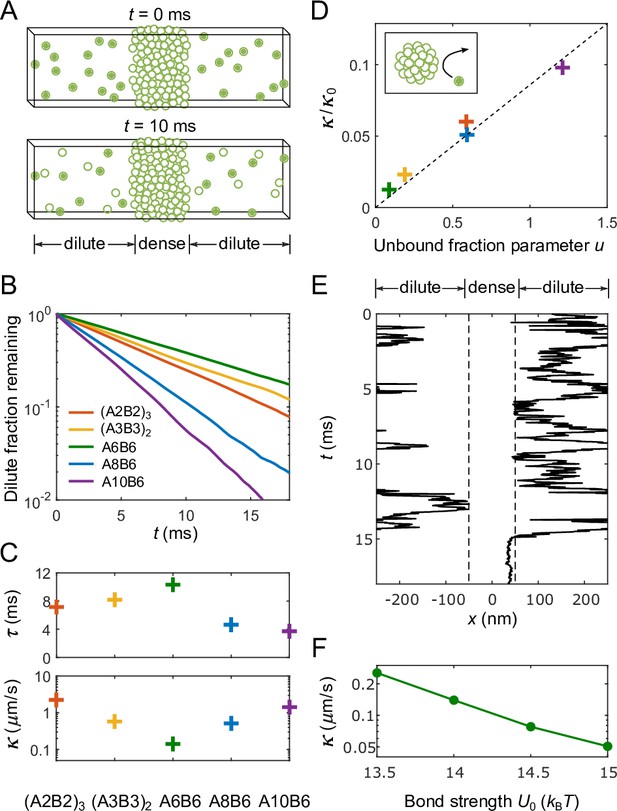
Determination of interface conductance from simulations.

(A) Illustration of simulation protocol: At $t = 0$ only polymers in the dilute phase are ‘labeled’ (solid balls), any polymer that enters the dense phase (forms an A-B bond lasting >10 times the average bond lifetime of an isolated A-B pair) becomes permanently ‘unlabeled’ (hollow balls). (B) Fraction of labeled polymers in the dilute phase as a function of time for simulations of the five types of polymers shown in Figure 2A. (C) Decay time of labeled polymers from exponential fits to curves in (B) (top), and corresponding calculated values of interface conductance $κ$ (bottom). (D) For all simulated polymers, interface conductance scaled by $κ_{0}$ (Equation 13) is approximately a linear function of a parameter $u$ which reflects the fraction of unbound stickers in the dense and dilute phases. Inset illustration: Polymers in the dilute phase with few or no unbound stickers may ‘bounce’ off the dense phase, which contributes to the interface resistance. (E) Example of simulated trajectory in which a dilute-phase A6B6 polymer ‘bounces’ multiple times before finally joining the dense phase. (F) Interface conductance $κ$ of A6B6 system as a function of binding strength $U_{0}$ between A and B stickers.

Figure 4

Download asset Open asset

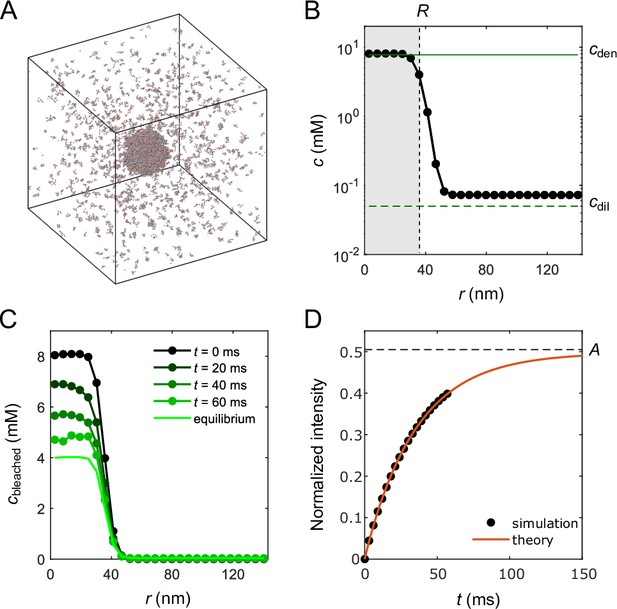
Molecular-dynamics simulations of in silico ‘FRAP experiment’ on a small droplet of A6B6 polymers.

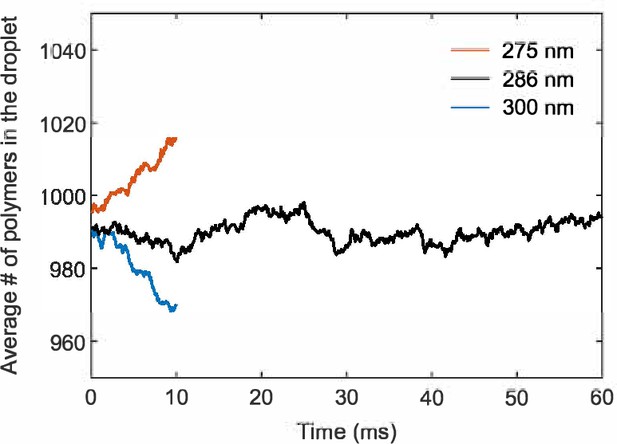
(A) Snapshot of 2000 A6B6 polymers in a 286 nm × 286 nm × 286 nm box with periodic boundary conditions. The system phase separates into a dense droplet (middle) and a surrounding dilute phase. (B) Polymer concentration profile for the simulation in (A) with the center of the droplet aligned to the origin and averaged over time and over 10 simulation repeats. The dilute- and dense-phase concentrations obtained from simulations in the slab geometry are denoted by green lines. The effective radius $R$ of the droplet is determined through $4 π R^{3} c_{den}^{d} / 3 + (V_{box} - 4 π R^{3} / 3) c_{dil}^{d} = N_{total}$ , where $V_{box}$ is the volume of the simulation box and $N_{total}$ is the total number of polymers. (C) Average concentration profile of bleached population measured at different times. (D) Comparison of the FRAP recovery curves obtained by tracking the simulated fraction of unbleached molecules inside the droplet as a function of time (black dots) and by numerical integration (red curve) of Equation 1 in a sphere of the same volume as $V_{box}$ using the measured parameters of the droplet system: $c_{den}^{d} = 8.1 mM$ , $c_{dil}^{d} = 0.073 mM$ , $D_{den} = 0.013 μ m^{2} / s$ , $D_{dil} = 17 μ m^{2} / s$ , $R = 0.037 μ m$ , and $κ^{d} = 0.20 μ m / s$ . For details of simulation and theory, refer to Appendix 2.

Figure 5

Download asset Open asset

FRAP recovery patterns for large versus small droplets can be notably different for condensates with a sufficiently large interface resistance.

(A) Expected relaxation time as a function of droplet radius for in silico ‘FRAP experiments’ on the A6B6 system. The interface resistance dominates recovery times for smaller droplets, whereas dense-phase diffusion dominates recovery times for larger droplets. Green circle: FRAP recovery time obtained from direct simulation of an A6B6 droplet of radius 37 nm. Black curve: the recovery time as a function of droplet radius from a single exponential fit of the exact solution of the recovery curve from Equation 1–4. Gray curve: the recovery time predicted by Equation 6. Yellow, blue, and red curves: the recovery time when dense-phase, dilute-phase, and interface flux limit the exchange dynamics, i.e., the first, second, and last term in Equation 6, respectively. Parameters matched to the simulated A6B6 system in the slab geometry: $c_{den} = 7.7 mM$ , $c_{dil} = 0.05 mM$ , $D_{den} = 0.013 μ m^{2} / s$ , $D_{dil} = 17 μ m^{2} / s$ , and $κ = 0.14 μ m / s$ . (B) Time courses of fluorescence profiles for A6B6 droplets of radius $1 μ m$ (top) and $0.1 μ m$ (bottom); red is fully bleached, green is fully recovered. These concentration profiles are the numerical solutions of Equations 1–3 using parameters provided in (A).

Appendix 1—figure 1

Download asset Open asset

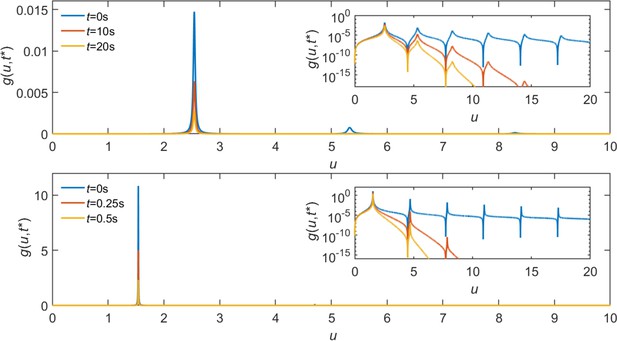
Representative curves of $g (u, t^{*})$ .

Parameters matched to the simulated $A 6 B 6$ system: $c_{den} = 7.7 mM$ , $c_{dil} = 0.05 mM$ , $D_{den} = 0.013 µ m^{2} / s$ , $D_{dil} = 17 µ m^{2} / s$ , and $κ = 0.14 µ m / s$ . Droplet radius is $R = 1 µ m$ (top) and $0.1 µ m$ (bottom). Inset: same plot with the $y$ -axis in log scale.

Appendix 1—figure 2

Download asset Open asset

Comparison of exact and approximate solutions of Equation 24.

Inset: percentage error of the approximate solution.

Appendix 2—figure 1

Download asset Open asset

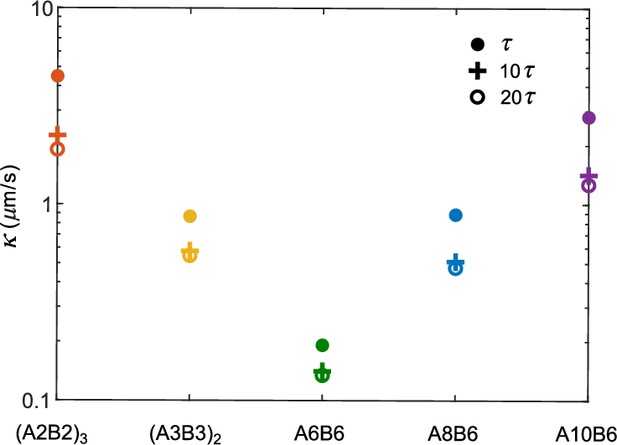
Interface conductance inferred from average survival time of particles initially in the dilute phase for different criteria for having ‘joined’ the dense phase (Figure 3).

The interface conductance is shown for three criteria: a polymer is considered to have joined the dense phase if it is in the dense-phase cluster for a continuous duration of $τ$ , $10 τ$ , or $20 τ$ , where $τ$ is the average bond lifetime of an isolated A-B sticker pair.

Appendix 2—figure 2

Download asset Open asset

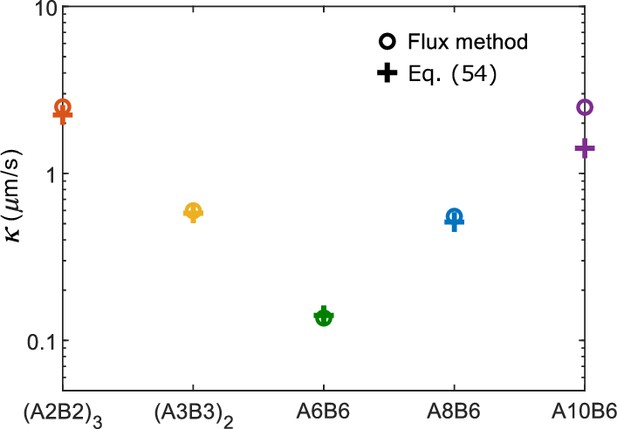
Comparison of interface conductance $κ$ obtained with the flux method and with Equation 54 as reported in Figure 3C.

Appendix 2—figure 3

Download asset Open asset

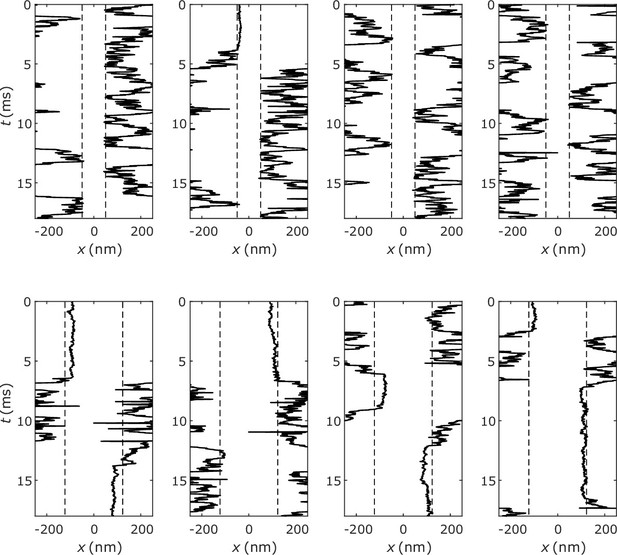
Representative trajectories of molecules ‘bouncing’ multiple times at the interface of the A6B6 system (top) and A10B6 system (bottom).

Appendix 2—figure 4

Download asset Open asset

A simulation box of side length 286 nm stabilizes the droplet size.

Number of polymers in the droplet as a function of time averaged over 10 simulation replicates for simulation boxes of side length 275 nm, 286 nm, and 300 nm.

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/91680/elife-91680-mdarchecklist1-v1.docx
Download elife-91680-mdarchecklist1-v1.docx
Source code 1 MATLAB scripts used to generate input files for the LAMMPS Molecular Dynamics Simulator, as well as the corresponding LAMMPS input files.: https://cdn.elifesciences.org/articles/91680/elife-91680-code1-v1.zip
Download elife-91680-code1-v1.zip

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Article PDF

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Yaojun Zhang
Andrew GT Pyo
Ross Kliegman
Yoyo Jiang
Clifford P Brangwynne
Howard A Stone
Ned S Wingreen

(2024)

The exchange dynamics of biomolecular condensates

eLife 12:RP91680.

https://doi.org/10.7554/eLife.91680.3

Sign up for email alerts

Privacy notice