Factorized visual representations in the primate visual system and deep neural networks
- Zuckerman Mind Brain Behavior Institute, Columbia University, United States
- Department of Neuroscience, Columbia University, United States
Figures
Figure 1
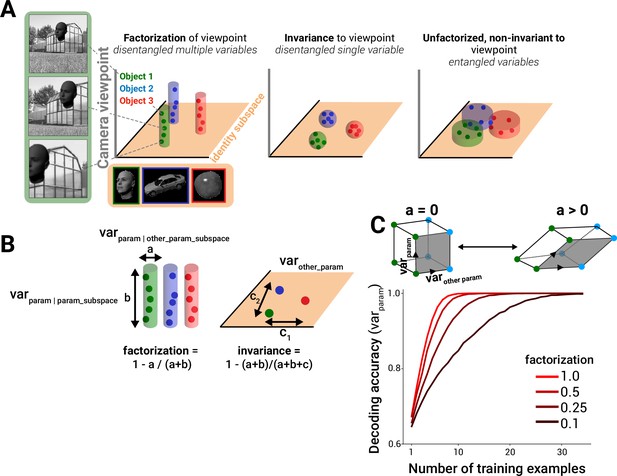
Framework for quantifying factorization in neural and model representations.
(A) A subspace for encoding a variable, for example, object identity, in a linearly separable manner can be achieved by becoming invariant to non-class variables (compact spheres, middle column, where the volume of the sphere corresponds to the degree of neural invariance, or tolerance, for non-class variables; colored dots represent example images within each class) and/or by encoding variance induced by non-identity variables in orthogonal neural axes to the identity subspace (extended cylinders, left column). Only the factorization strategy simultaneously represents multiple variables in a disentangled fashion. A code that is sensitive to non-identity parameters within the identity subspace corrupts the ability to decode identity (right column) (identity subspace denoted by orange plane). (B) Variance across images within a class can be measured in two different linear subspaces: that containing the majority of variance for all other parameters (a, ‘other_param_subspace’) and that containing the majority of the variance for that parameter (b, ‘param_subspace’). Factorization is defined as the fraction of parameter-induced variance that avoids the other-parameter subspace (left). By contrast, invariance to the parameter of interest is computed by comparing the overall parameter-induced variance to the variance in response to other parameters (c, ‘var_other_param’) (right). (C) In a simulation of coding strategies for two binary variables out of 10 total dimensions that are varying (see ‘Methods’), a decrease in orthogonality of the relationship between the encoding of the two variables (alignment a > 0, or going from a square to a parallelogram geometry), despite maintaining linear separability of variables, results in poor classifier performance in the few training-samples regime when i.i.d. Gaussian noise is present in the data samples (only 3 of 10 dimensions used in simulation are shown).
Figure 2 with 1 supplement
Benefit of factorization to neural decoding in macaque V4 and IT.
(A) Factorization of object identity and position increased from macaque V4 to IT (PCA-based factorization, see ‘Methods’; dataset E1 – multiunit activity in macaque visual cortex) (left). Like factorization, invariance also increased from V4 to IT (note, ‘identity’ refers to invariance to all non-identity position factors, solid black line) (right). Combined with increased factorization of the remaining variance, this led to higher invariance within the variable’s subspace (orange lines), representing a neural subspace for identity information with invariance to nuisance parameters which decoders can target for read-out. (B) An experiment to test the importance of factorization for supporting object class decoding performance in neural responses. We applied a transformation to the neural data (linear basis rotation) that rotated the relative positions of mean responses to object classes without changing the relative proportion of within- vs. between-class variance (Equation 1 in ’Methods’). This transformation preserved invariance to non-class factors (leftmost pair of bars in each plot), while decreasing factorization of class information from non-class factors (center pair of bars in each plot). Concurrently, it had the effect of significantly reducing object class decoding performance (light vs. dark red bars in each plot, chance = 1/64; n = 128 multi-unit sites in V4 and 128 in IT).
Figure 2—figure supplement 1
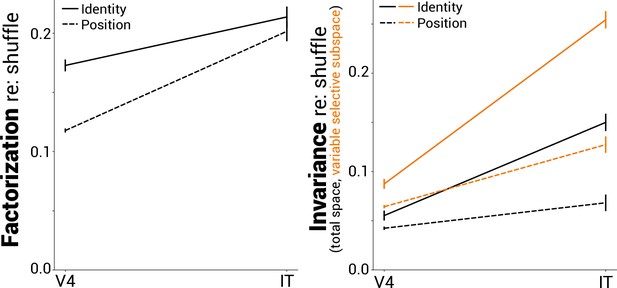
Factorization and invariance in V4 and IT neural data.
Normalized factorization and invariance as in Figure 2A but after subtracting shuffle control for V4 and IT neural datasets. Shuffling the image identities of each population vector accounts for increases in factorization driven purely by changes in the covariance statistics of population responses between V4 and IT. However, the normalized factorization scores remained significantly above zero for both brain areas.
Figure 3
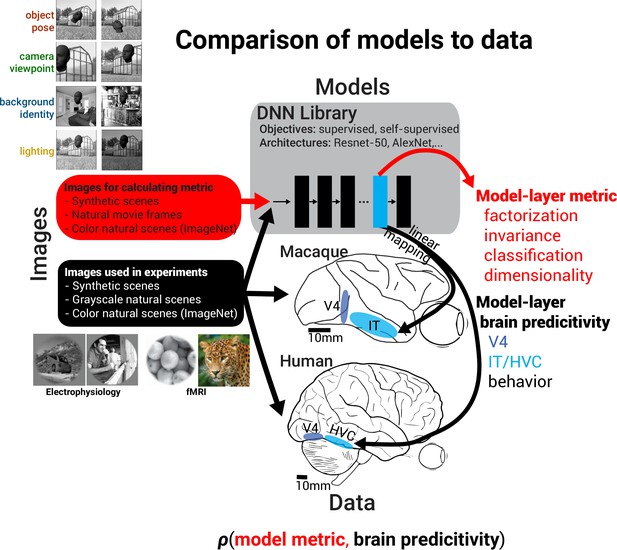
Measurement of factorization in deep neural network (DNN) models and comparison to brain data.
Schematic showing how meta-analysis on models and brain data was conducted by first computing various representational metrics on models and then measuring a model’s predictive power across a variety of datasets. For computing the representational metrics of factorization of and invariance to a scene parameter, variance in model responses was induced by individually varying each of four scene parameters (n = 10 parameter levels) for each base scene (n = 100 base scenes) (see images on the top left). The combination of model-layer metric and model-layer dataset predictivity for a choice of model, layer, metric, and dataset specifies the coordinates of a single dot on the scatter plots in Figures 4 and 7, and the across-model correlation coefficient between a particular representational metric and neural predictivity for a dataset summarizes the potential importance of the metric in producing more brainlike models (see Figures 5 and 6).
Figure 4 with 3 supplements
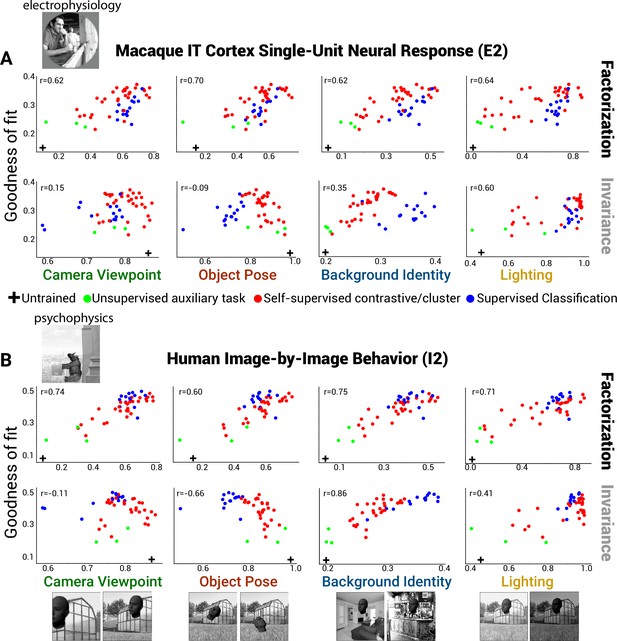
Neural and behavioral predictivity of models versus their factorization and invariance properties.
(A) Scatter plots, for example, neural dataset (IT single units, macaque E2 dataset) showing the correlation between a model’s predictive power as an encoding model for IT neural data versus a model’s ability to factorize or become invariant to different scene parameters (each dot is a different model, using each model’s penultimate layer). Note that factorization (PCA-based, see ‘Methods’) in trained models is consistently higher than that for an untrained, randomly initialized Resnet-50 DNN architecture (rightward shift relative to black cross). Invariance to background and lighting but not to object pose and viewpoint increased in trained models relative to the untrained control (rightward versus leftward shift relative to black cross). (B) Same as (A) except for human behavior performance patterns across images (human I2 dataset). Increasing scene parameter factorization in models generally correlated with better neural predictivity (top row). A noticeable drop in neural predictivity was seen for high levels of invariance to object pose (bottom row, second panel).
Figure 4—figure supplement 1
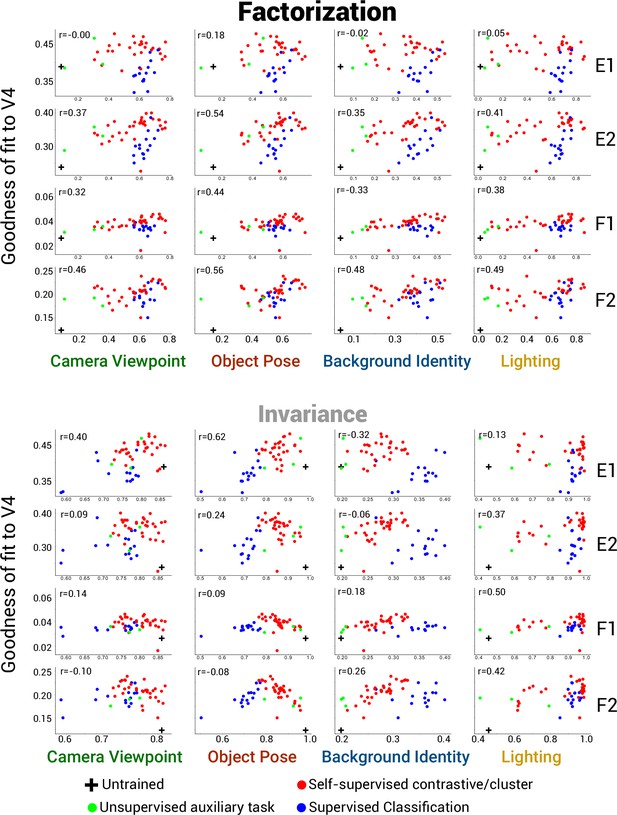
Scatter plots for all datasets for V4.
Scatter plots as in Figure 4A and B for all datasets. Brain metric (y-axes) is macaque neuron/human voxel fits in V4 cortex. The plots in the top half use deep neural network (DNN) factorization scores (PCA-based method) on the x-axis while the bottom half use DNN invariance scores.
Figure 4—figure supplement 2
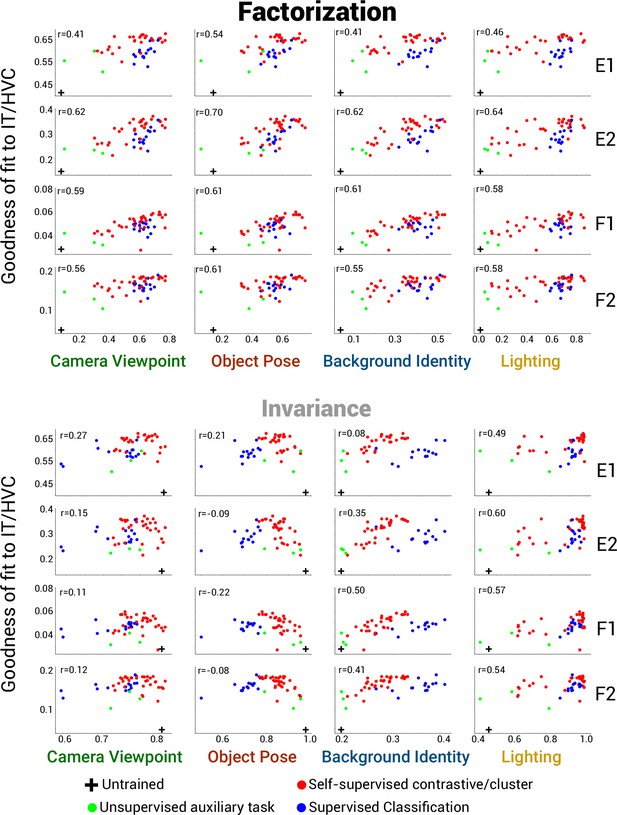
Scatter plots for all datasets for ITC/HVC.
Scatter plots as in Figure 4A and B for all datasets. Brain metric (y-axes) is macaque neuron/human voxel fits in ITC/HVC. The plots in the top half use DNN factorization scores (PCA-based method) on the x-axis while the bottom half use DNN invariance scores.
Figure 4—figure supplement 3
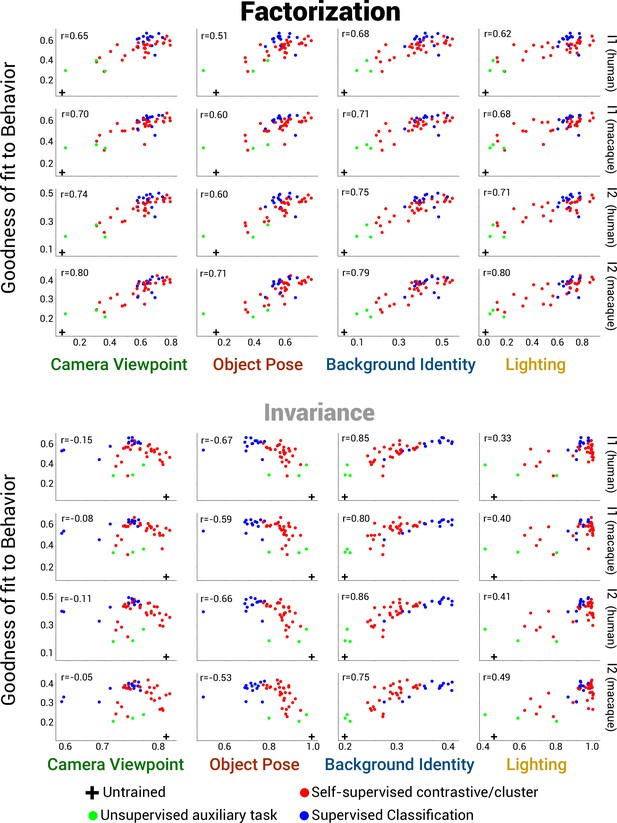
Scatter plots for all datasets for behavior.
Scatter plots as in Figure 4A and B for all datasets. Brain metric (y-axes) is macaque/human per-image classification performance (I1) and image-by-distractor class performance (I2). The plots in the top half use deep neural network (DNN) factorization scores (PCA-based method) on the x-axis while the bottom half use DNN invariance scores.
Figure 5 with 3 supplements
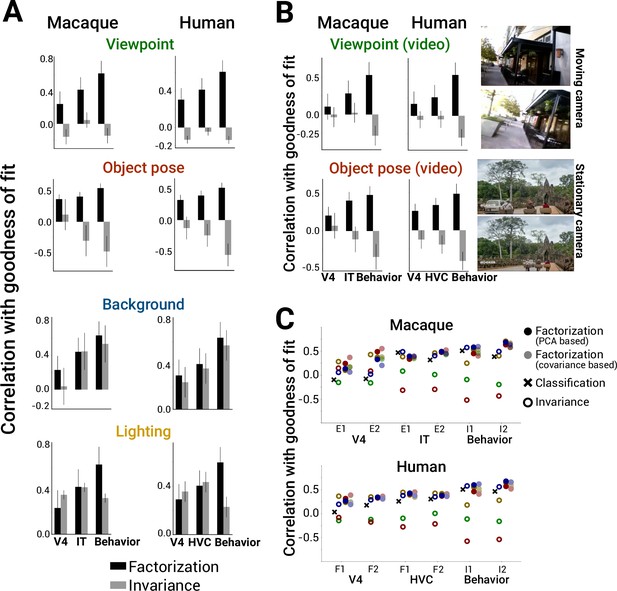
Scene parameter factorization correlates with more brainlike deep neural network (DNN) models.
(A) Factorization of scene parameters in model representations computed using the PCA-based method consistently correlated with a model being more brainlike across multiple independent datasets measuring monkey neurons, human fMRI voxels, or behavioral performance in both macaques and humans (left vs. right column) (black bars). By contrast, increased invariance to camera viewpoint or object pose was not indicative of brainlike models (gray bars). In all cases, model representational metric and neural predictivity score were computed by averaging scores across the last 5 model layers. (B) Instead of computing factorization scores using our synthetic images (Figure 3, top left), recomputing camera viewpoint or object pose factorization from natural movie datasets that primarily contained camera or object motion, respectively, gave similar results for predicting which model representations would be more brainlike (right: example movie frames; also see ’Methods’). Error bars in (A and B) are standard deviations over bootstrapped resampling of the models. (C) Summary of the results from (A) across datasets (x-axis) for invariance (open symbols) versus factorization (closed symbols) (for reference, ‘x’ symbols indicate predictive power when using model classification performance). Results using a comparable, alternative method for computing factorization (covariance-based, Equation 4 in ’Methods’; light closed symbols) are shown adjacent to the original factorization metric (PCA-based, Equation 2 in ‘Methods’; dark closed symbols).
Figure 5—figure supplement 1
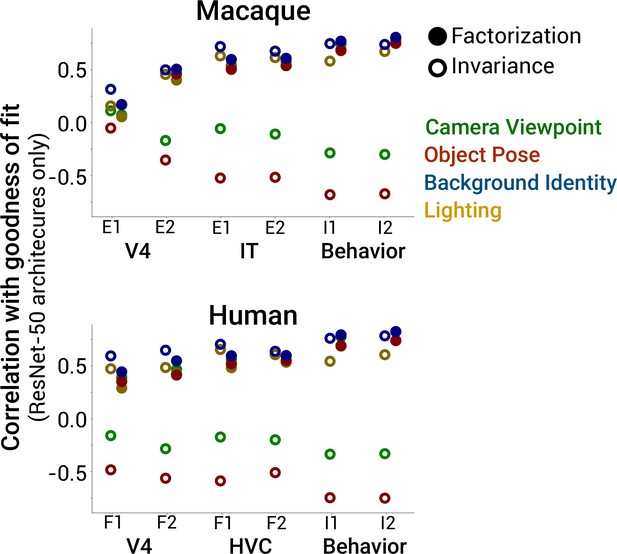
Predictivity of factorization and invariance restricting to ResNet-50 model architectures.
Same format as Figure 5C except with the analyses restricted to using only models with the Resnet-50 architecture. The main finding of factorization of scene parameters in deep neural networks (DNNs) being generally positively correlated with better predictions of brain data is replicated using this architecture-matched subset of models, controlling for potential confounds from model architecture.
Figure 5—figure supplement 2
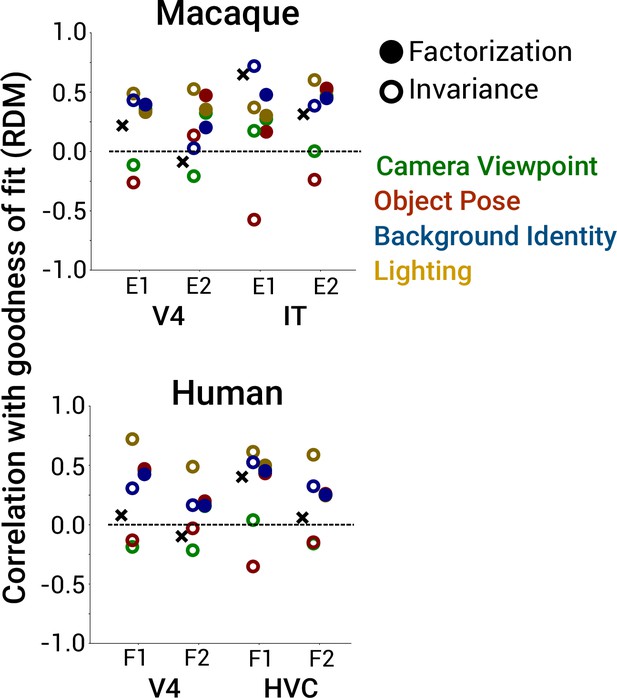
Predictivity of factorization and invariance for representational dissimilarity matrices (RDMs).
Same format as Figure 5C except for predicting population RDMs of macaque neurophysiological and human fMRI data (in Figure 5C, linear encoding fits of each single neuron/voxel were used to measure brain predictivity of a model). The main finding of factorization of scene parameters in deep neural networks (DNNs) being positively correlated with better predictions of brain data is replicated using RDMs instead of neural/voxel goodness of encoding fit.
Figure 5—figure supplement 3
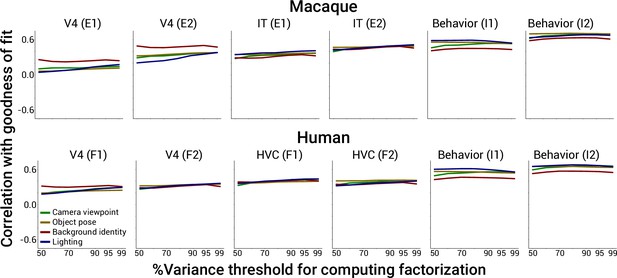
Effect on neural and behavioral predictivity of PCA threshold for computing PCA-based factorization, related to Figure 5.
The % variance threshold used in the main text for estimating a PCA linear subspace capturing the bulk of the variance induced by all other parameters besides the parameter of interest is somewhat arbitrary. Here, we show that the results of our main analysis change little if we vary this parameter from 50 to 99%. In the main text, a PCA threshold of 90% was used for computing PCA-based factorization scores.
Figure 6
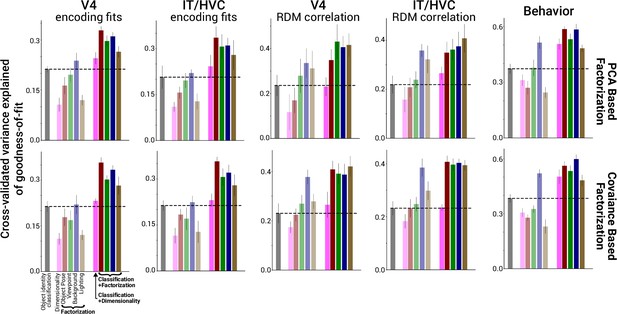
Scene parameter factorization combined with object identity classification improves correlations with neural predictivity.
Average across datasets of brain predictivity of classification (faded black bar), dimensionality (faded pink bar), and factorization (remaining faded colored bars) in a model representation. Linearly combining factorization with classification in a regression model (unfaded bars at right) produced significant improvements in predicting the most brainlike models (performance cross-validated across models and averaged across datasets, n = 4 datasets for each of V4, IT/HVC and behavior). The boost from factorization in predicting the most brainlike models was not observed for neural and fMRI data when combining classification with a model’s overall dimensionality (solid pink bars; compared to black dashed line for brain predictivity when using classification alone). Results are shown for both the PCA-based and covariance-based factorization metric (top versus bottom row). Error bars are standard deviations over bootstrapped resampling of the models.
Figure 7
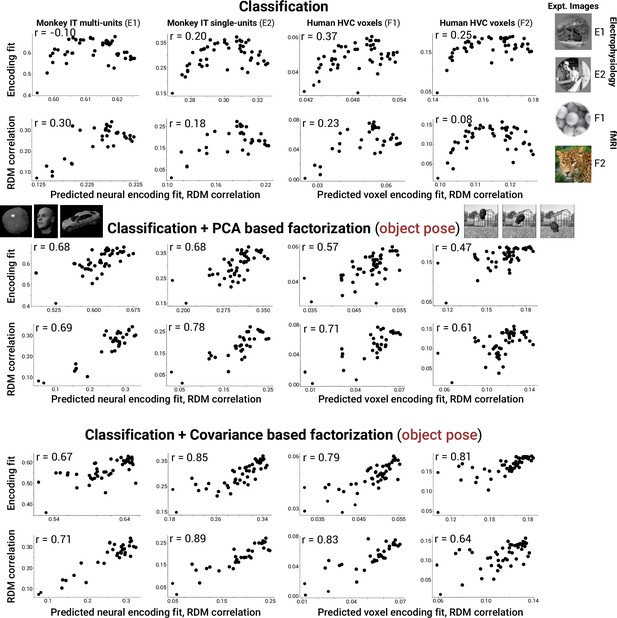
Combining classification performance with object pose factorization improves predictions of the most brainlike models on IT/HVC data.
Example scatter plots for neural and fMRI datasets (macaque E1 and E2, IT multi units and single units; human F1 and F2, fMRI voxels) showing a saturating and sometimes reversing trend in neural (voxel) predictivity for models that are increasingly good at classification (top row). This saturating/reversing trend is no longer present when adding object pose factorization to classification as a combined, predictive metric for brainlikeness of a model (middle and bottom rows). The x-axis of each plot indicates the predicted encoding fit or representational dissimilarity matrix (RDM) correlation after fitting a linear regression model with the indicated metrics as input (either classification or classification + factorization).
Additional files
-
Supplementary file 1
Tables of datasets and models used.
(a) Table of datasets used for measuring similarity of models to the brain. Datasets from both macaque and human high-level visual cortex as well as high-level visual behavior were collated for testing the brainlikeness of computational models. For neural and fMRI datasets, the features in the model were used to predict the image-by-image response pattern of each neuron or voxel. For behavior datasets, the performance of linear decoders built atop model representations were compared to performance per image of macaques and humans. (b) Table of models tested. For each model, we measured representational factorization and invariance in each of the final five layers of the model as well as evaluating their brainlikeness using the datasets in (a).
- https://cdn.elifesciences.org/articles/91685/elife-91685-supp1-v1.docx
-
MDAR checklist
- https://cdn.elifesciences.org/articles/91685/elife-91685-mdarchecklist1-v1.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Factorized visual representations in the primate visual system and deep neural networks
eLife 13:RP91685.
https://doi.org/10.7554/eLife.91685.3
