Heritable epigenetic changes are constrained by the dynamics of regulatory architectures
- University of Maryland, United States
Figures
Figure 1 with 3 supplements
The simplest heritable regulatory architectures.
Of the 99 possible regulatory architectures with fewer than four entities (see Figure 1—figure supplement 3), only 26 can be indefinitely heritable (A through Z with x, y, and z entities/sensors). Entities that act as sensors (black circles) or that do not provide any regulatory input (blue circles), or that provide positive (green arrows) or negative (magenta bar) regulatory interactions are indicated.
Figure 1—figure supplement 1
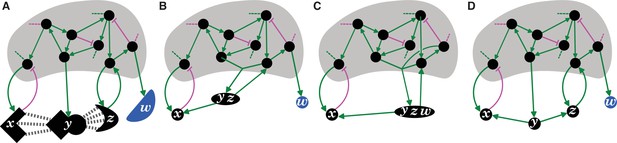
Entity-Sensor-Property systems provide a principled way of parsing regulators and their interactions in living systems.
(A) Schematic of regulatory interactions in a living system, highlighting incomplete knowledge, but including some regulators that detect the shape(s) of others. Entities that act as sensors (black circles and black shapes) by providing regulatory input in response to changes in other entities or that do not provide any regulatory input (blue shape), interactions that promote (green arrows) or inhibit (magenta bar) a property of downstream entities/sensors, interactions with unknown entities/sensors (dotted lines), and the unknown larger network (grey shading) are depicted. (B and C) Two ways of parsing the interactors that combine some regulators together (y and z in (B), and y, z, and w in (C)) and therefore do not reflect the natural properties salient to the system in (A). (D) Deduced regulatory architecture with sensors (x, y, z; red) and entities (w; blue) parsed to better reflect the system depicted in (A). Progression from the depiction in (B) or (C) to that in (D) requires experiments that consider the separable entities (x, y, z and w), sensors (x, y and z), and the sensed properties (y’s square edges for sensor x, and its curved surfaces for sensor z) that are relevant for the system.
Figure 1—figure supplement 2
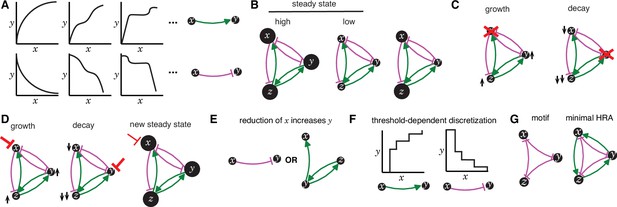
Illustrations of key concepts.
(A) Regulatory interactions can lead to a variety of dependencies between two entities. Alternative relationships (left) when x promotes y (top) or when x inhibits y (bottom) and their generic representations (right; green arrow = promote and magenta bar = inhibit). In general, the relationship between any two entities in a living system requires empirical investigation. (B) The same regulatory architecture (HRA ‘Y’ from Figure 1) can be present at different states with relatively high (left) or proportionally low (middle) levels of all entities (areas of circles) at steady state, or with unregulated levels of different entities (right) away from steady state (e.g., soon after a perturbation). (C) After permanent loss of an entity (red x), the remaining entities can show uncontrolled growth (left, up arrow) or eventual decay (right, down arrow) depending on the residual architecture. (D) After transient reduction in the levels of an entity (red bar), the remaining entities can show uncontrolled growth (left), eventual decay (middle), or recovery to a new steady state level (right) depending on the residual architecture and the strength/duration of the perturbation. (E) Two equivalent inferences based on an observation after a perturbation whereby reduction in x increases y. Either x inhibits y (left) or y promotes x and itself via z (right). (F) The thresholds required for interactions between entities discretize the changes caused by promotions (left) or inhibitions (right) in living systems. (G) An regulatory motif composed of three repressors (left) needs at least three positive regulatory interactions to be heritable (right).
Figure 1—figure supplement 3
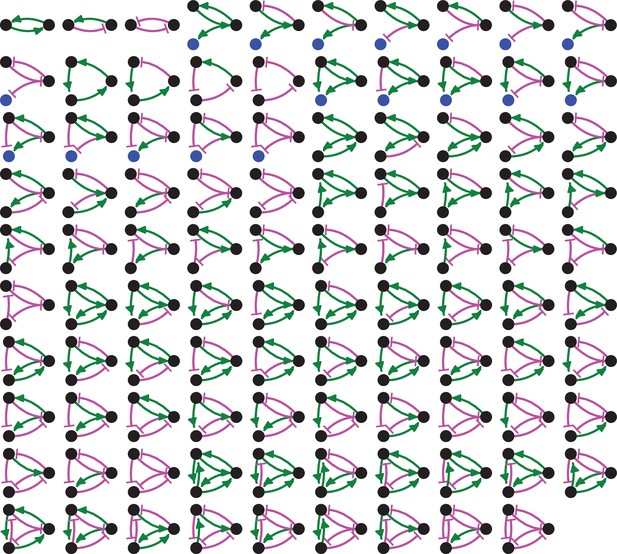
Adding regulation to the 8 simple heritable architectures generates 99 regulated architectures, not all of which are heritable.
Entities that act as sensors (black circles) or that do not provide any regulatory input (blue circles), positive (green arrows) and negative (magenta bar) regulatory interactions are indicated.
Figure 2 with 7 supplements
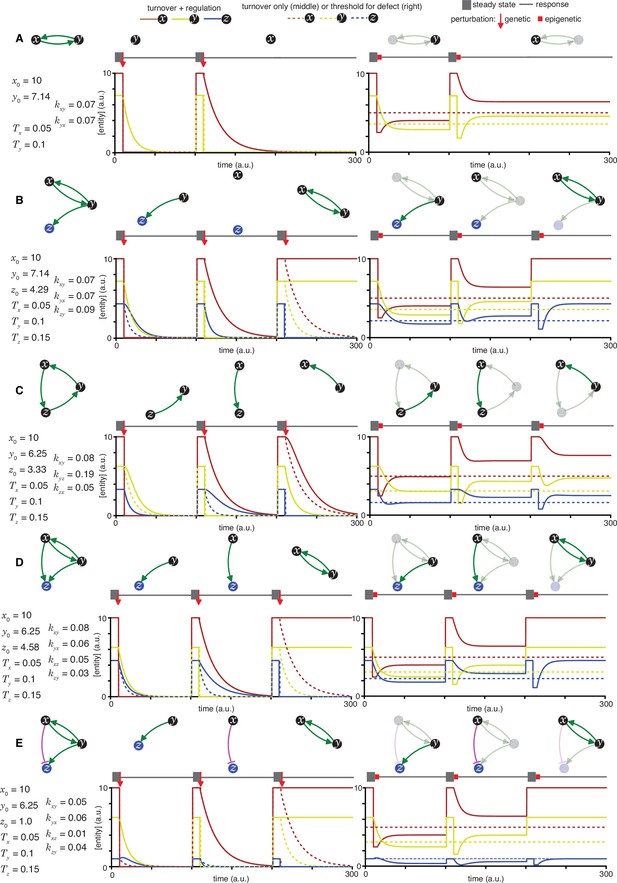
Epigenetic and genetic changes can provide complementary information about heritable regulatory architectures.
(A to H) In each panel, cases where specific perturbations of architectures (top left) characterized by sets of parameters that support a steady state (bottom left) result in different outcomes for permanent or genetic (middle) versus transient or epigenetic (right) changes are illustrated. Relative concentrations of each entity during periods of steady state (thick grey line), the point of genetic change (red arrow), periods of epigenetic reduction (red bar, for a duration tp = 5 (a.u); with the threshold for observing a defect d=0.5; and an extent of perturbation beyond the threshold p=0.5), and periods of recovery after perturbation (thin grey line) are shown. Architectures are depicted as in Figure 1 (A, B, C, D, E, F, G and H depict the heritable regulatory architectures A, G, P, R, W, X, Y and Z, respectively) with transient reductions in an entity or sensor and associated interactions depicted using lighter shades. Dotted lines indicate unregulated turnover (in middle) or thresholds for observing defects upon reduction in levels of an entity/sensor (in right).
Figure 2—figure supplement 1
Heritable regulatory architectures with one loop.
Loss-of-function perturbations of each entity (x, y, or z, if present) in architectures (left top) characterized by sets of parameters that support a steady state (left bottom) are illustrated. The behaviour of residual architectures after permanent or genetic (middle) and transient or epigenetic (right) changes are illustrated. Period of steady state (thick grey line), the point of genetic change (red arrow), duration of epigenetic reduction (red bar, for a duration tp = 5 (a.u); with the threshold for observing a defect d=0.5; and an extent of perturbation beyond the threshold p=0.5), and duration of recovery after perturbation (thin grey line) were simulated. Architectures are depicted as in Figure 1 (A, B, C, D, and E depict the heritable regulatory architectures A, B, C, D, and E, respectively) with transient reductions in an entity and associated interactions depicted using lighter shades. Dotted lines indicate unregulated turnover (in middle) or thresholds for observing defects upon reduction in levels of an entity (in right).
Figure 2—figure supplement 2
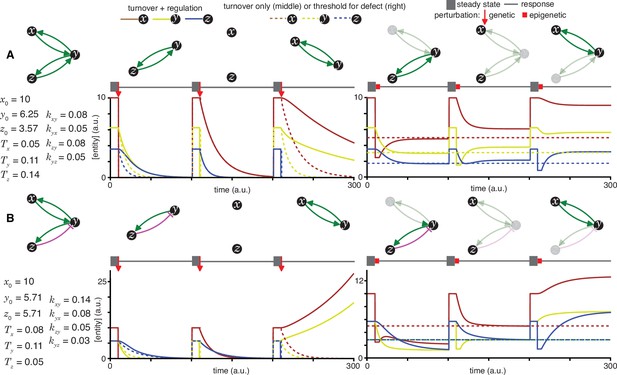
Heritable regulatory architectures with two loops and a shared node.
Architectures and their responses to perturbations are depicted as in Figure 2—figure supplement 1 (A and B depict the heritable regulatory architectures F and G, respectively).
Figure 2—figure supplement 3
Heritable regulatory architectures with two loops and a shared edge.
Architectures and their responses to perturbations are depicted as in Figure 2—figure supplement 1 (A, B, and C depict the heritable regulatory architectures H, I, and J, respectively).
Figure 2—figure supplement 4
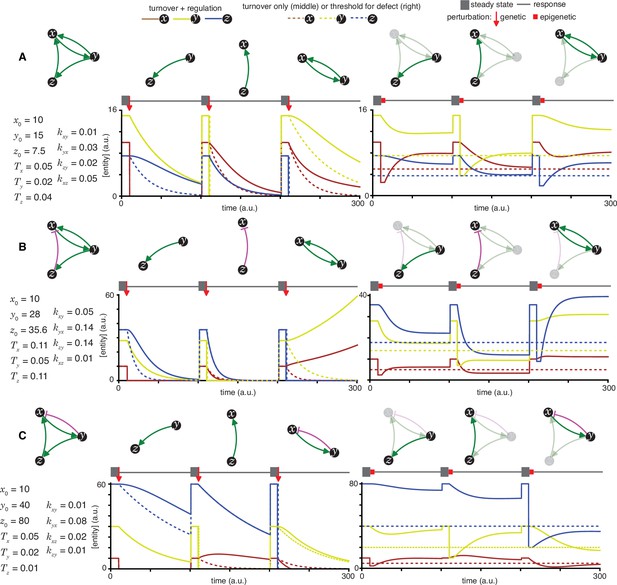
Heritable regulatory architectures with two loops, a shared node, a connecting edge, and up to one negative regulatory interaction.
Architectures and their responses to perturbations are depicted as in Figure 2—figure supplement 1 (A, B, C, D, and E depict the heritable regulatory architectures K, L, M, N, and O, respectively).
Figure 2—figure supplement 5
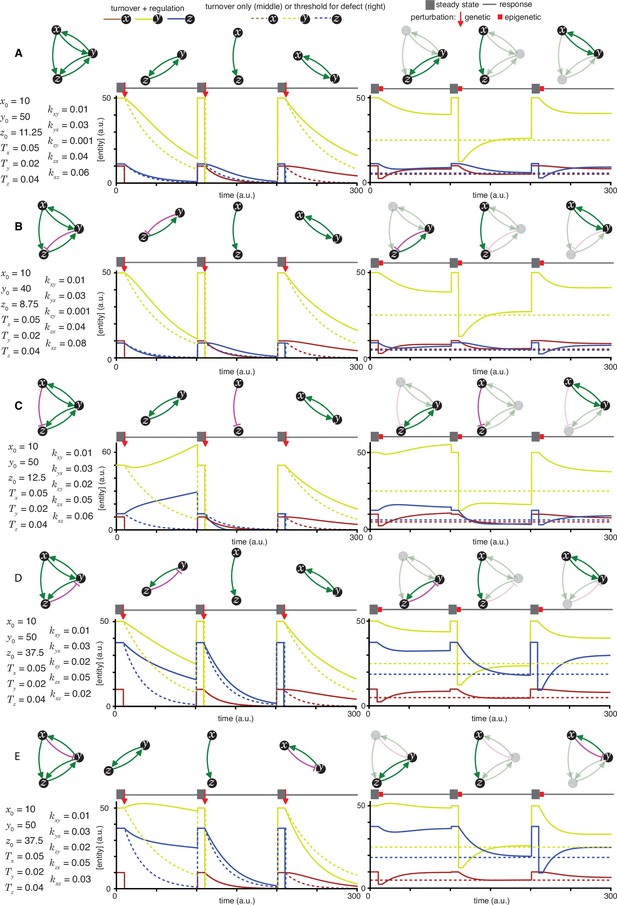
Heritable regulatory architectures with two loops, a shared node, a connecting edge, and two negative regulatory interaction.
Architectures and their responses to perturbations are depicted as in Figure 2—figure supplement 1(A, B, C, and D depict the heritable regulatory architectures P, Q, R, and S, respectively).
Figure 2—figure supplement 6
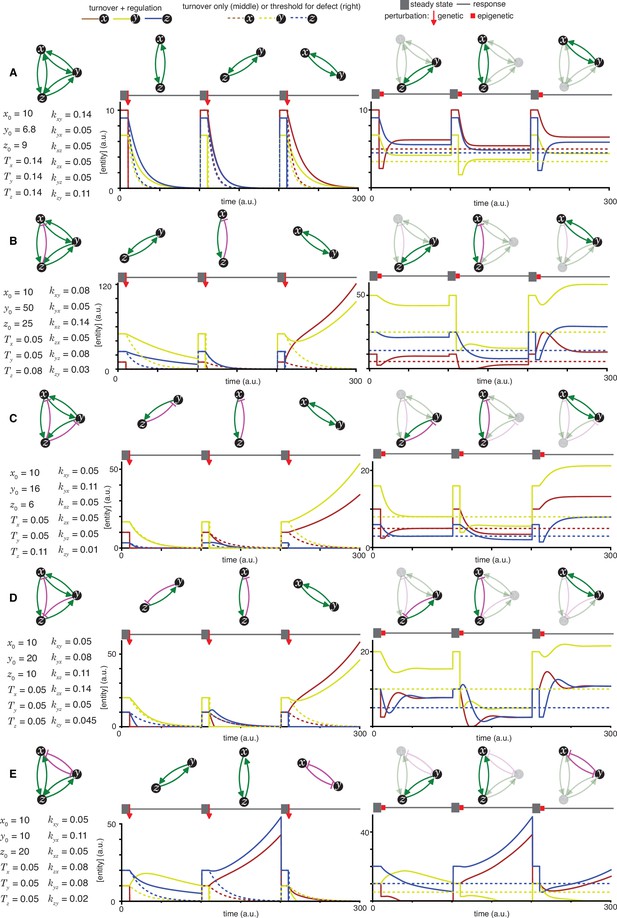
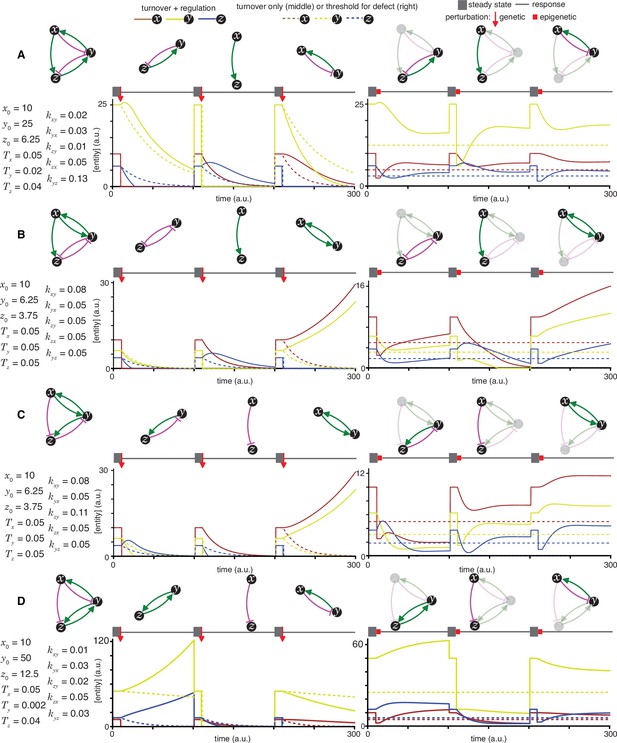
Heritable regulatory architectures formed by complete graphs with up to two negative regulatory interactions.
Architectures and their responses to perturbations are depicted as in Figure 2—figure supplement 1 (A, B, C, D and E depict the heritable regulatory architectures T, U, V, W, and X respectively).
Figure 2—figure supplement 7
Heritable regulatory architectures formed by complete graphs with three negative regulatory interactions.
Architectures and their responses to perturbations are depicted as in Figure 2—figure supplement 1 (A and B depict the heritable regulatory architectures Y and Z, respectively).
Figure 3
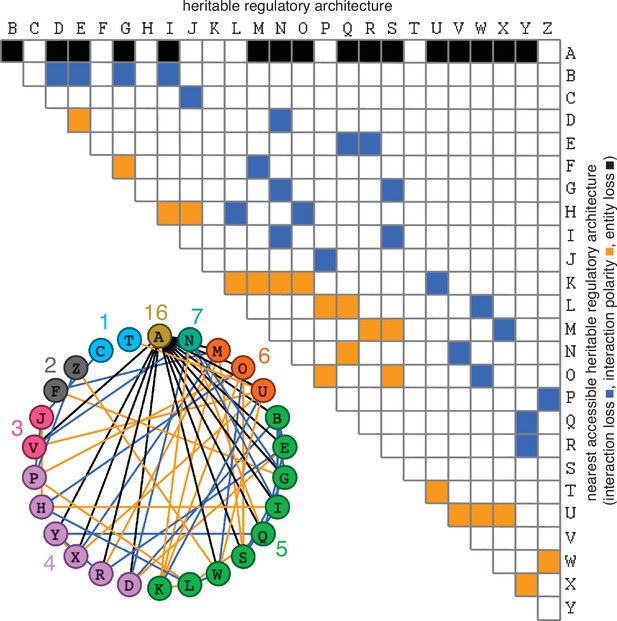
Possible conversions between the simplest heritable regulatory architectures.
Table summarizing the possible changes in regulatory architecture observed after a single perturbation from steady state (blue, loss of a regulatory interaction; orange, change in the polarity of a regulatory interaction; black, either change in regulatory interaction and/or loss of an entity). For example, Z can arise from P through the loss of a regulatory interaction or from W through a change in the polarity of a regulatory interaction. Bottom left, Network diagram summarizing possible changes arranged clockwise by frequency of change to the HRA (color-matched numbers). Edges (black, blue, or orange) are colored as in table and nodes are colored according to number of adjacent HRAs.
Figure 4 with 3 supplements
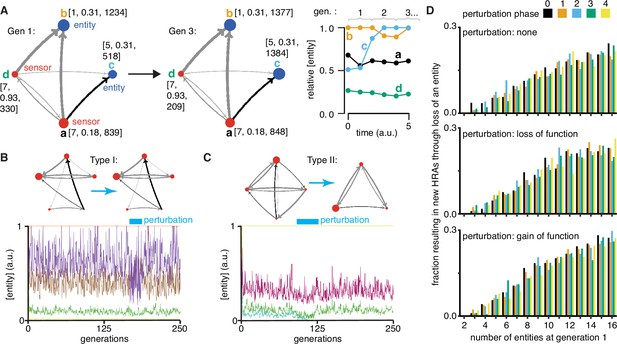
Regulatory architectures can be simulated as entity-sensor-property systems to examine how they persist or change in response to transient perturbations.
(A) An ESP system illustrating the stability of a regulatory architecture despite changes in the relative numbers of the interactors (entities/sensors) over time. Left, Simulation of an ESP system showing how interacting molecules create regulatory architectures. This system consists of four entities (a, b, c, d), where ‘d’ and ‘a’ are also sensors. Each sensor (red) sends regulatory input (grey, positive or black, negative) to increase or decrease another sensor or entity (blue). Numbers of each entity (i.e., its property value) change in fixed steps per unit time. The number of sensors needed to cause one unit of change in property differs for each regulatory input (lower number = thicker line, representing lower threshold for downstream change). Each entity is depicted with property step, active fraction, and number at the start of the first generation (gen 1) and at the end of the third generation (gen 3). Right, The relative numbers of the entities, which can be together considered as ‘phenotype’, can change over time. Note that relative amounts of ‘a’, ‘b’, or ‘d’ remain fairly constant, but that of ‘c’ changes over time. (B and C) ESP systems can differ in their response to epigenetic change. Top, ESP systems are depicted as in A. Bottom, Relative abundance of each entity/sensor (different colors) or ‘phenotype’ across generations. Blue bars = times of epigenetic perturbation (reduction by two fold). In response to epigenetic perturbation that lasts for a few generations, Type I systems recover without complete loss of any entity/sensor (B) and Type II systems change through loss of an entity/sensor (C). (D) ESP systems of varying complexity can show heritable epigenetic changes, depending on when the system is perturbed. The numbers of randomly chosen entities were unperturbed (none, top), reduced to half the minimum (loss of function), or increased to twice the maximum (gain of function, bottom) every 50 generations for 2.5 generations and the number of systems responding with a new stable regulatory architecture that lasts for >25 generations were determined. Perturbations were introduced at each of five different time points with respect to the starting generation (phase - 0,1,2,3,4). Of the 78,285 stable systems, 14,180 showed heritable epigenetic change.
Figure 4—figure supplement 1
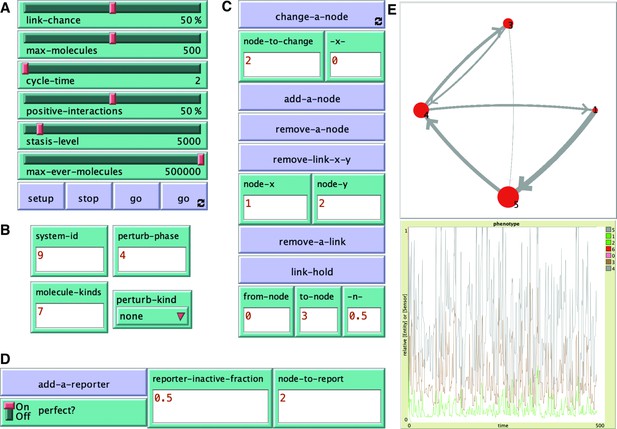
Key features of the ESP system explorer.
A simulation of ESP systems was made using the agent-based modeling software NetLogo with controls for making a variety of changes. (A) Sliders and buttons for set up and simulation of an ESP system: link-chance, max-molecules, cycle-time, positive-interactions, stasis-level, max-ever-molecules, setup, stop, go, and go forever. (B) Parameters for specifying a particular system: system-id, molecule-kinds, perturb-phase, and perturb-kind. (C) Buttons and input for making changes to the system during the simulation. change-a-node, add-a-node, remove-a-node, remove-link-x-y (node-x, node-y), remove-a-link, and link-hold (from-node, to-node, -n-). (D) Buttons and input for adding a reporter of any node. add-a-reporter, perfect?, reporter-inactive-fraction, and node-to-report. (E) Representative output of changing regulatory architecture (top) and relative amounts of interactors representing ‘phenotype’ (bottom) over time. See Video 1 for examples examining impact of changes and code (ESP_systems_single_system_explorer_v1.nlogo) for detailed information.
Figure 4—figure supplement 2
Example of a system with long but finite stability.
This system (62795) begins with 6 entities/sensors, but after an early loss of one sensor, the remaining 5 are maintained as part of a HRA until 59,882.5 generations. See Figure 2 - figure supplement 7 and code (ESP_systems_single_system_explorer_v1.nlogo) for detailed information.
Figure 4—figure supplement 3
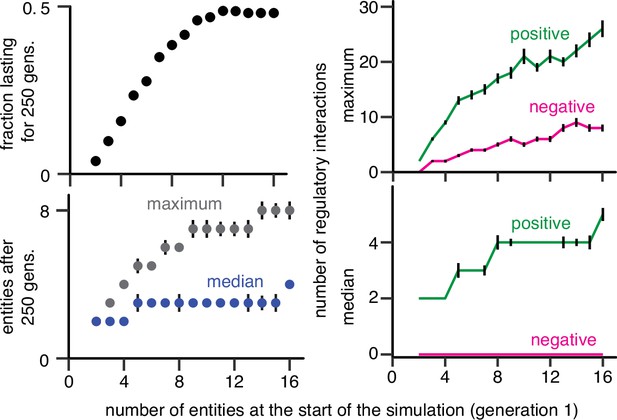
Characteristics of randomly sampled HRAs simulated with partitioning of entities during each cell division or generation and periodic perturbations.
Top left, Fractions of ESP systems that persist with or without heritable epigenetic change for 250 generations when simulations were begun with different numbers of molecules. Bottom left, Maximum (grey) and median (blue) numbers of entities/sensors in ESP systems at the end of 250 generations when simulations were begun with different numbers of molecules. Top right, Maximal numbers of positive and negative regulatory interactions at the end of 250 generations when simulations were begun with different numbers of molecules. Bottom right, Median numbers of positive and negative regulatory interactions at the end of 250 generations when simulations were begun with different numbers of molecules.
Figure 5
ESP systems that incorporate the timings of cell division during C. elegans development and temporal delays in regulatory interactions can recreate periods of increased expression in every generation.
(A) Top, Schematic of cell divisions between two successive generations of C. elegans. Cells that maintain the intergenerational continuity through cell divisions (magenta, germline), cells that cannot contribute to the next generation through cell divisions (white, soma) but arise in each generation (gen x and gen x+1) from the bottleneck stage, and the interactions between these two cell types (red line) are depicted. Bottom, Experimentally determined timing of cell division (1) versus growth (0) from one zygote to the next in C. elegans in 15 min intervals (=1 time step in simulations), which give a generation time of ~91.25 hr (=365 time steps). See Supplementary file 3 for the relative timing of cell divisions based on past studies. (B) Key control features for simulating HRAs that incorporate organismal timing of cell divisions and temporal delays in regulation. In addition to controls used in the single system explorer (Figure 4—figure supplement 1), the following sliders were added: one to set the number of generations of ancestors that can contribute regulation (ancestral-effect-generations, e.g., 2 for parental effects), one to set the probability of the regulatory origin for each interaction from one of the two sensors that form the positive feedback loop required for heritability (cyc1-vs-cyc2), and one to set the probability of the gene of interest being a sensor providing regulatory input into the positive feedback loop instead of an entity (gene-is-sensor). Monitors that show the current generation and the total number of molecules, and an input to set the system-id were also added. (C) Representative simulated HRA that incorporates temporal delays and the characteristic timings of cell divisions in C. elegans. Different types of positive (+) and negative (-) regulators (red) that depend on cis-regulatory sequences (+s and -s, e.g. transcription factors), and that depend on the gene product (+p and -p for gene and reporter, for example small RNAs made using mRNA template, chaperones that promote the folding of the protein, etc.) are depicted with color coded arrows (+, grey and -, black). Different relative delays in regulation (hours on arrows, maximum of 2 x generation time to allow for the widely observed parental regulation) are also depicted. The unknown components of the core positive feedback loops required for heredity were simulated as two sensors that promote each other’s production in addition to the production of all other entities/sensors. (D) Relative concentrations of entities/sensors regulated by the HRA in (C) over 10 generations showing transgenerational waveforms. Properties, active fractions, relative numbers, and regulatory interactions were considered and relative numbers of each entity/sensor depicted as in Figure 4 with colors as in (C). Although the simulation began with random numbers for all entities/sensors, the HRA settles into a reproducible pattern within two generations with periods of increased relative concentrations for some entities/sensors in every generation (red asterisks). Also see Video 13.
Figure 6 with 1 supplement
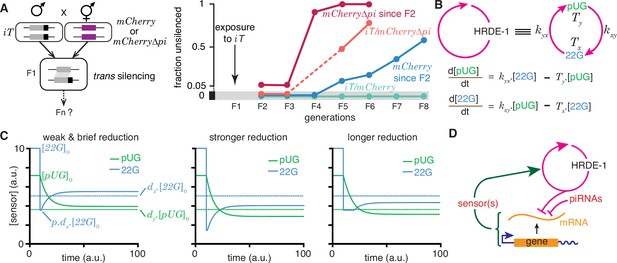
Regulation of a positive feedback loop can explain the magnitude and duration of experimentally observed heritable RNA silencing.
(A) Experimental evidence from C. elegans for susceptibility to, recovery from, and resistance to trans silencing by a silenced gene(A) has been adapted from Figure 5A of Devanapally et al., 2021). Left, Schematic of experiment showing a gene silenced for hundreds of generations by mating-induced silencing (iT = mex-5p::mCherry::h2b::tbb-2 3’ utr::gpd-2 operon::gfp::h2b::cye-1 3’ utr) exposed to genes with matching sequences (mCherry and mCherry∆pi, i.e. mCherry without piRNA binding sites) to initiate trans silencing. Right, Dynamics of heritable RNA silencing showing the initial exposure to trans silencing by iT (F1 generation), subsequent recovery after separation from iT (‘mCherry since F2’ and ‘mCherry∆pi since F2’), resistance to silencing by iT (iT/mCherry∆pi), or persistence of silencing by iT (iT/mCherry). Fractions of animals that recover mCherry or mCherry∆pi expression (fraction unsilenced) are depicted with error bars eliminated for simplicity. (B) Abstraction of the HRDE-1-dependent positive feedback loop required for the persistence of RNA silencing. Top, Representation of the mutual production of RNA intermediates (22G and pUG) with rates of production (kyx and kxy) and turnover (Tx and Ty). Bottom, Ordinary differential equations for the rates of change of pUG RNAs (pUG) and 22G RNAs (22G). See text for details. (C) Impact of transient epigenetic perturbations on subsequent activity of a positive feedback loop. Left, response to a brief and weak reduction in the levels of one sensor (22G) of the positive feedback loop. The steady-state levels after recovery were above the threshold required for a silencing effect (dotted lines). Steady states (), perturbation level (), and levels required for silencing () are indicated. Middle and Right, Stronger (middle) or longer (right) reduction can result in steady-state levels after recovery being below the threshold required for a silencing effect (dotted lines). (D) Deduced regulatory architecture that explains data shown in (A) by including enhancement of silencing by piRNA binding on target mRNA and a gene-specific inhibitory loop that can act across generations through as yet unidentified sensor(s). Prolonged silencing in prg-1(-) animals (Shukla et al., 2021) suggests that these sensor(s) are among the genes mis-regulated in prg-1(-) animals (e.g. Reed et al., 2020). See Figure 6—figure supplement 1 for depictions of additional equivalent architectures.
Figure 6—figure supplement 1
Equivalent representations of a transgenerational feedback loop that can tune HRDE-1-dependent heritable RNA silencing.
Left, the architecture proposed in Figure 6d, whereby a sensor(s) that promotes an HRDE-1-dependent positive feedback loop is reduced in response to changes in a gene or its gene products caused by the activity of the HRDE-1-dependent positive feedback loop, making it self-limiting. Middle, An architecture where the feedback from the gene to HRDE-1-dependent loop is via the inhibition of an inhibition instead of an activation. Right, An architecture as in left, but that includes additional CSR-1-dependent positive feedback loops that could amplify the transgenerational inhibition of the HRDE-1-dependent loop.
Videos
Video 1
NetLogo run showing the single-system explorer with sample interactions with the simulation.
Video 2
Example ESP system with system-id 46357 without any perturbation.
Video 3
Example ESP system with system-id 46357 and with loss-of-function perturbations in phase 0.
Video 4
Example ESP system with system-id 46357 and with loss-of-function perturbations in phase 1.
Video 5
Example ESP system with system-id 46357 and with loss-of-function perturbations in phase 2.
Video 6
Example ESP system with system-id 46357 and with loss-of-function perturbations in phase 3.
Video 7
Example ESP system with system-id 46357 and with loss-of-function perturbations in phase 4.
Video 8
Example ESP system with system-id 46357 and with gain-of-function perturbations in phase 0.
Video 9
Example ESP system with system-id 46357 and with gain-of-function perturbations in phase 1.
Video 10
Example ESP system with system-id 46357 and with gain-of-function perturbations in phase 2.
Video 11
Example ESP system with system-id 46357 and with gain-of-function perturbations in phase 3.
Video 12
Example ESP system with system-id 46357 and with gain-of-function perturbations in phase 4.
Video 13
NetLogo run showing an ESP system with regulatory delays and developmental timing of cell divisions adapted from experimental results in C. elegans.
Tables
Table 1
Capacity of heritable regulatory architectures to store information.
The number of heritable, regulated, and heritably regulated architectures, and the information they can store were calculated using a program that enumerates non-isomorphic weakly connected graphs that satisfy specified criteria (‘Heritable_Regulatory_Architectures_1–4_entities.py’).
| Entities | Heritable | Regulated | Heritably regulated | Bits of information |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | - |
| 2 | 1 | 3 | 1 | 0 |
| 3 | 7 | 96 | 25 | 4.64 |
| 4 | 125 | 19,559 | 5604 | 12.45 |
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Software, algorithm | Python | https://www.python.org/downloads/release/python-385/ | ||
| Software, algorithm | R | https://cran.r-project.org/bin/macosx/ | ||
| Software, algorithm | NetLogo | https://ccl.northwestern.edu/netlogo/ | ||
| Software, algorithm | Gephi | https://gephi.org/ |
Additional files
-
Supplementary file 1
Parameters that generate steady states for the 26 simplest HRAs.
- https://cdn.elifesciences.org/articles/92093/elife-92093-supp1-v1.xlsx
-
Supplementary file 2
Behavior of Entity-Sensor-Property systems that have some persistent architecture after 250 generations.
- https://cdn.elifesciences.org/articles/92093/elife-92093-supp2-v1.xlsx
-
Supplementary file 3
The timing of C. elegans cell divisions along the germline.
- https://cdn.elifesciences.org/articles/92093/elife-92093-supp3-v1.xlsx
-
Supplementary file 4
Behavior of regulatory architectures that incorporate the developmental time of C. elegans.
- https://cdn.elifesciences.org/articles/92093/elife-92093-supp4-v1.xlsx
-
MDAR checklist
- https://cdn.elifesciences.org/articles/92093/elife-92093-mdarchecklist1-v1.docx
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Heritable epigenetic changes are constrained by the dynamics of regulatory architectures
eLife 12:RP92093.
https://doi.org/10.7554/eLife.92093.3
