Figures and data in Neural evidence of functional compensation for fluid intelligence in healthy ageing

Figures
Tables
Additional files

4 figures, 2 tables and 1 additional file

Figures

Figure 1

Download asset Open asset

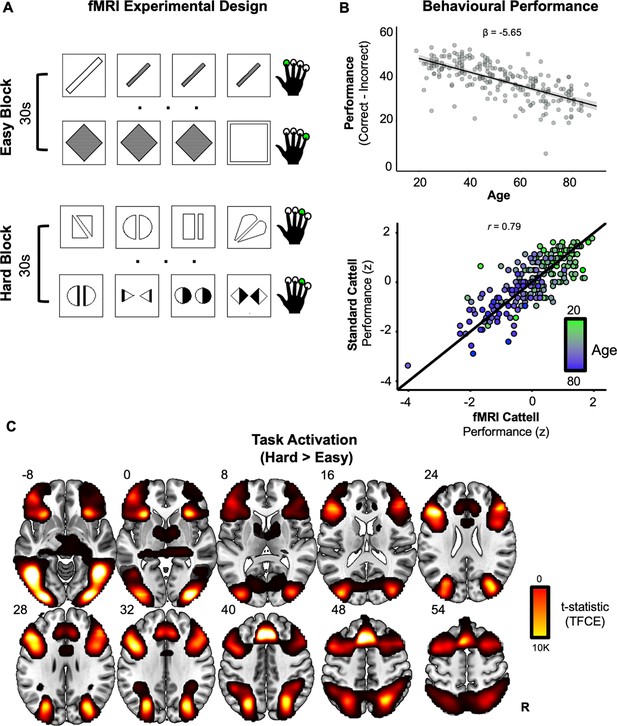
Experimental design, behavioural performance and task activation effects.

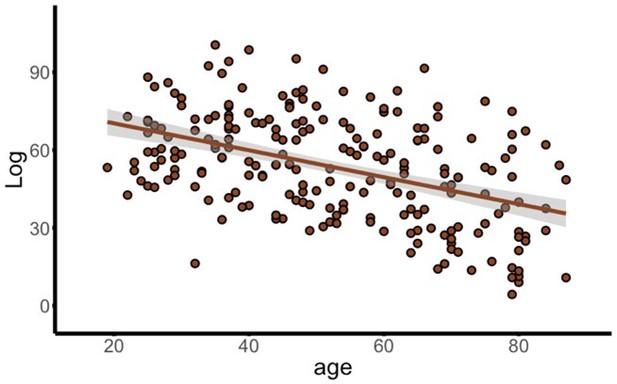
(A) Functional magnetic resonance imaging (fMRI) version of Cattell task. On each trial (each row), participants select the odd-one-out from four panels with a single finger button-press (green circles). Condition blocks (30 s) alternate between easy vs. hard puzzles. (B) Behavioural age-related decline. Performance (correct minus incorrect in fMRI version of Cattell task) significantly declined linearly with age (upper). High reliability was observed between performance measures from the standard Cattell task and the modified version used for fMRI (lower). In the upper panel, the black line represents the fitted-regression estimates with shaded 95% confidence intervals. In the lower panel, the black line represents perfect correlation between the two Cattell versions. (C) Univariate task effect. Whole-brain voxel-wise activations for solving the puzzles in the hard, relative to easy, blocks, after threshold-free cluster enhanced (TFCE) correction (slices are labelled with z MNI coordinates).

Figure 2

Download asset Open asset

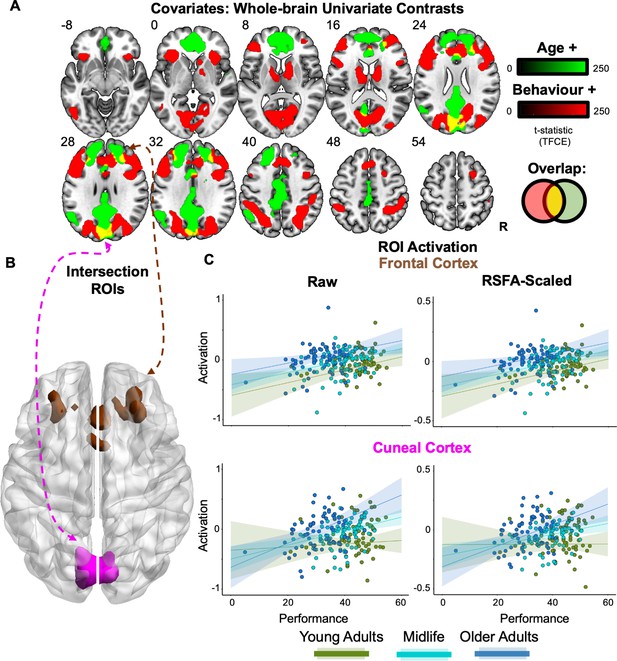
Univariate analysis.

(A) Whole-brain effects of age and performance. Age (green) and performance (red) positively predicted unique aspects of increased task activation, with their spatial overlap (yellow) being overlaid on a template MNI brain, using p < 0.05 threshold-free cluster enhanced (TFCE) with z MNI coordinate labels. (B) Intersection regions of interest (ROIs). A bilateral cuneal (magenta) and frontal cortex (brown) ROI were defined from voxels that showed a positive and unique effect of both age and performance (yellow map in A). (C) ROI activation. Activation (raw = left; Resting State Fluctuation Amplitude [RSFA]-scaled = right) is plotted against behavioural performance based on a tertile split between three age groups (19–44, 45–63, and 64–87 years).

Figure 3

Download asset Open asset

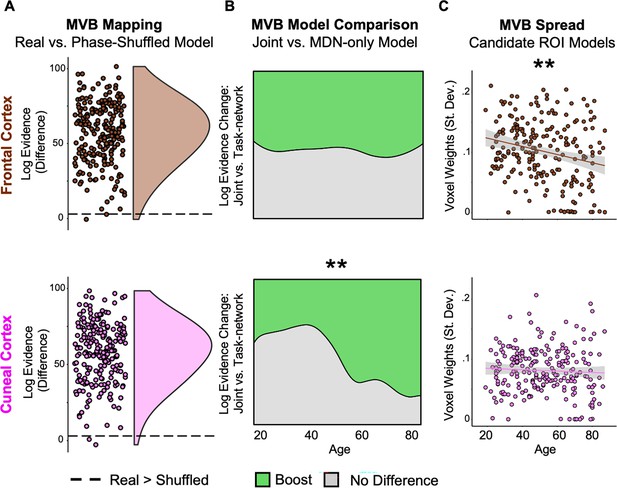
Multivariate analysis.

(A) Multivariate Bayesian (MVB) decoding. Points represent the difference in log evidence per participant (for the real vs. shuffled model) for the joint model using activation patterns to decode the [Hard > Easy] contrast. (B) Boost likelihood model comparison. Across age, a smoothed density estimate represents the likelihood that there was a boost (of log evidence >3; green) or no difference (grey) to model evidence per participant when decoding models included activation patterns from either of the compensation regions of interest (ROIs) (Figure 2B) in addition to the multiple demand network (MDN) (Figure 1C), relative to a model that sampled only from the MDN. A significant positive linear effect of age on boost likelihood was observed for the cuneal (lower) but not frontal ROI (upper). (C) MVB spread. Points represent the spread (standard deviation) of multivariate responses, showing a reduction with age in frontal cortex. ** denotes p < 0.01.

Author response image 1

Download asset Open asset

Negative effect of age on MVB log evidence model outcomes for frontal cortex.

Tables

Table 1

Standardised coefficients in multiple regression predicting functional magnetic resonance imaging (fMRI) activation (Hard − Easy) as a function of Age and Performance for the two regions of interest (ROIs) identified in Figure 2.

Note that the p-values for the main effects of Age and Performance are biased by the selection of these voxels. RSFA = scaled by Resting-State Fluctuation Amplitudes (see text).

Region	Coefficient	Estimate	t value	p
Cuneal
	Constant term	−0.06	−2.57	0.011
	Age	0.09	3.57	<0.001
	Performance	0.08	3.21	0.002
	Sex	−0.05	−2.59	0.01
	Age × Performance	0.04	2.21	0.028
Cuneal (RSFA)
	Constant term	−0.03	−2.60	0.010
	Age	0.04	3.24	0.001
	Performance	0.04	3.11	0.002
	Sex	−0.02	−2.52	0.013
	Age × Performance	0.02	1.97	0.049
Frontal
	Constant term	−0.03	−2.02	0.045
	Age	0.08	4.24	<0.001
	Performance	0.08	4.54	<0.001
	Sex	<0.001	−0.35	0.728
	Age × Performance	<0.001	−0.15	0.882
Frontal (RSFA)
	Constant term	−0.02	−1.99	0.048
	Age	0.04	4.12	<0.001
	Performance	0.04	4.48	<0.001
	Sex	0.00	−0.37	0.709
	Age × Performance	0.00	−0.13	0.898

Table 2

Standardised coefficients in multivariate Bayesian (MVB) multiple logistic regression analyses predicting boost likelihood as a function of age or the spread of voxel weights (with Sex and Mean Univariate Activation as covariates).

Analysis	Model	Coefficient	Estimate	z/t-statistic	p
Boost likelihood
	Cuneal ROI + Task-network (166 voxels each)
		Constant term	2.17	8.79	<0.001
		Age	0.79	3.23	<0.001
		Sex	0.08	0.37	0.714
		Univariate	−0.34	−1.59	0.112
	Frontal ROI + Task-network (85 voxels each)
		Constant term	2.20	9.30	<0.001
		Age	0.04	0.19	0.851
		Sex	0.26	1.13	0.257
		Univariate	−0.54	−2.33	0.020
Spread (weights)
	Cuneal ROI
		Constant term	<−0.001	<0.001	>0.999
		Age	−0.06	−0.84	0.403
		Sex	−0.05	−0.64	0.521
		Univariate	0.01	0.09	0.932
	Frontal ROI
		Constant term	<−0.001	<0.001	>0.999
		Age	−0.19	−2.89	0.005
		Sex	−0.09	−1.37	0.171
		Univariate	0.09	1.33	0.185