Figures and data in Mapping spatial patterns to energetic benefits in groups of flow-coupled swimmers

Figures
Videos
Tables
Additional files

14 figures, 2 videos, 1 table and 1 additional file

Figures

Figure 1 with 4 supplements

Download asset Open asset

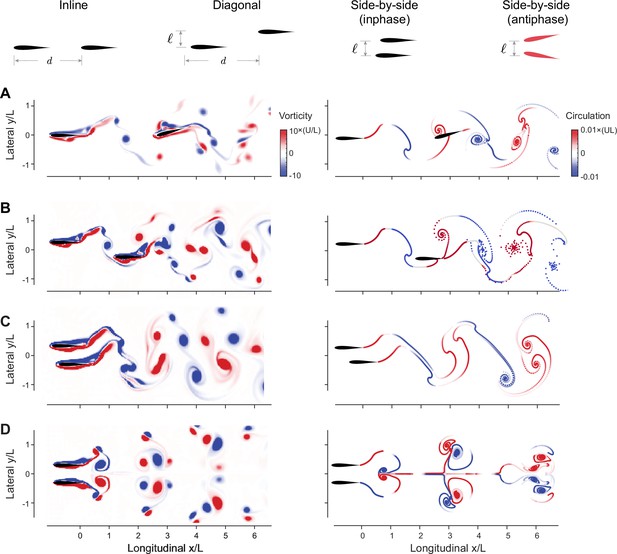
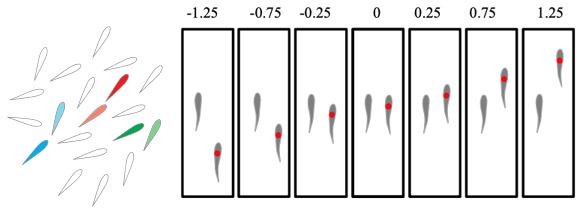
Flow-coupled swimmers self-organize into stable pairwise formations.

(A) Inline ( $ℓ = 0, ϕ = π / 2$ ), (B) diagonal ( $ℓ = L / 2, ϕ = 0$ ), (C) inphase side-by-side ( $ℓ = L / 2, ϕ = 0$ ), and (D) antiphase side-by-side ( $ℓ = L / 2, ϕ = π$ ) in computational fluid dynamics (CFD) (left) and vortex sheet (VS) (right) simulations. Power savings at steady state relative to respective solitary swimmers are reported in Figure 3. Parameter values are $A = 15^{\circ}$ , Re = $2 π ρ A f L / μ = 1645$ in CFD, and $f τ_{diss} = 2.45$ in VS simulations. Corresponding hydrodynamic moments are given in Figure 1—figure supplement 4. Simulations at different Reynolds numbers and dissipation times are given in Figure 1—figure supplements 1–3.

Figure 1—figure supplement 1

Download asset Open asset

Computational fluid dynamics (CFD) simulations of pairwise formations.

Vorticity field (left column) and flow agreement parameter $𝕍$ (right column) in the wake of a pair of inline and inphase swimmers Reynolds number $Re = 206$ (A), 308 (B), 411 (C), 1645 (D), respectively. The pitching amplitude of leader and follower is set to $A = 15^{\circ}$ , except in (A), where the follower is pitching at $A = 13 . 5^{\circ}$ .

Figure 1—figure supplement 2

Download asset Open asset

Vortex sheet (VS) simulations of pairwise formations.

Snapshots of the swimmers (left column) and flow agreement parameter $𝕍$ (right column) in the wake of a pair of swimmers in the VS model for dissipation time $2.45 T$ (A), $3.45 T$ (B), $4.45 T$ (C), and $9.45 T$ (D), respectively. The pitching amplitude is set to $A = 15^{\circ}$ , and the pitching frequency to $f = 1$ .

Figure 1—figure supplement 3

Download asset Open asset

Computational fluid dynamics (CFD) and vortex sheet (VS) simulations at various flow properties.

(A) Separation distance versus time in a pair of swimmers in the CFD model for five values of Reynolds numbers ${Re}_{A} = 206, 308, 411, 822, 1645$ (Figure 1—figure supplement 1). (B) Separation distance versus time in a pair of swimmers in the VS model for five values of dissipation time $τ_{diss} = 2.45 T, 3.45 T, 4.45 T, 9.45 T, \infty$ (Figure 1—figure supplement 2). Separation distance $d$ is normalized by swimming speed $U$ for each cases, respectively. In (A, B), the swimmers stabilize near $d / U T = 1$ . The pitching amplitude of leader and follower is set to $A = 15^{\circ}$ , except in ${Re}_{A} = 206$ , where the follower is pitching at $A = 13 . 5^{\circ}$ to avoid collision.

Figure 1—figure supplement 4

Download asset Open asset

Hydrodynamic moment acting on pairs of flapping swimmers.

(A) Inline ( $ℓ = 0, ϕ = 0$ ), (B) diagonal ( $ℓ = L / 4, ϕ = 0$ ), (C) inphase side-by-side ( $ℓ = L / 2, ϕ = 0$ ), and (D) antiphase side-by-side ( $ℓ = L / 2, ϕ = π$ ) in computational fluid dynamics (CFD) (left) and vortex sheet (VS) (right) simulations. For each simulation, we show the active torque $M_{a}$ exerted by the swimmers after a time $t_{s s}$ , ensuring that steady state has been reached. The non-reciprocity in the effects of leader on follower in inline and diagonal configuration is apparent. In the side-by-side configurations, a simple shift of the data in the inphase flapping case and a simple mirror symmetry in the antiphase flapping case would show that flow coupling is reciprocal.

Figure 2

Download asset Open asset

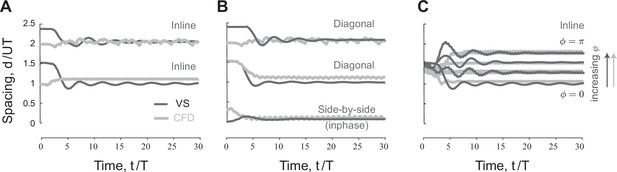
Emergent equilibria in pairwise formations.

(A) Time evolution of scaled streamwise separation distance $d / U T$ for a pair of inline swimmers at $ϕ = 0$ . Depending on initial conditions, the swimmers converge to one of two equilibria at distinct separation distance. (B) At $ℓ = L / 2$ , $d / U T$ changes slightly compared to inline swimming in (A). Importantly, a new side-by-side inphase equilibrium is now possible where the swimmers flap together at a slight shift in the streamwise direction. (C) Starting from the first equilibrium in (A), $d / U T$ increases linearly as we increase the phase lag $ϕ$ between the swimmers.

Figure 3

Download asset Open asset

Hydrodynamic benefits and linear phase-distance relationship in pairwise formations.

(A) Change in cost of transport compared to solitary swimmers for the inline, diagonal, side-by-side inphase, and side-by-side antiphase formations shown in Figure 1. (B) Emergent formations in pairs of swimmers in computational fluid dynamics (CFD) and vortex sheet (VS) models satisfy a linear phase-distance relationship, consistent with experimental (Ramananarivo et al., 2016; Newbolt et al., 2019; Li et al., 2020; Kurt et al., 2021; Thandiackal and Lauder, 2023) and numerical (Kim et al., 2010; Peng et al., 2018; Heydari and Kanso, 2021; Arranz et al., 2022) studies. With the exception of the antiphase side-by-side formation, swimmers in these formations have a reduced average cost of transport compared to solitary swimming.

Figure 4

Download asset Open asset

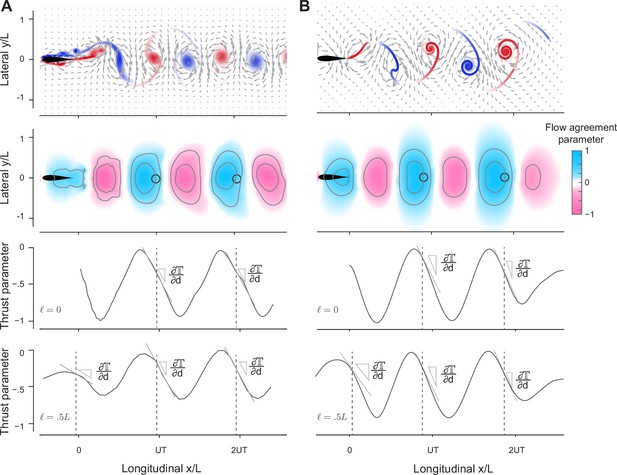
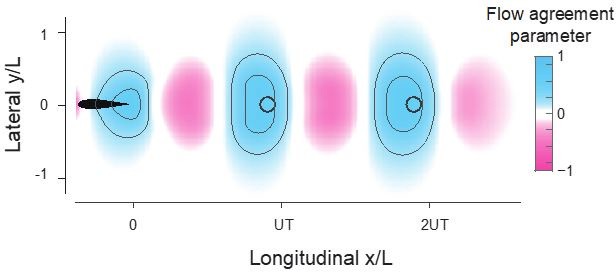
Prediction of relative equilibria in the wake of a solitary swimmer.

(A, B) Snapshots of vorticity and fluid velocity fields created by a solitary swimmer in computational fluid dynamics (CFD) and vortex sheet (VS) simulations and corresponding flow agreement parameter $𝕍$ fields for a virtual follower at $ϕ = 0$ . Locations of maximum $𝕍$ values (i.e. peaks in the flow agreement parameter field) coincide with the emergent equilibria in inphase pairwise formations (indicated by black circles). Contour lines represent flow agreement parameter at ±0.25, ±0.5. Thrust parameter $𝕋$ is shown at $ℓ = 0$ and $ℓ = 0.5 L$ . A negative slope $\partial 𝕋 / \partial d$ indicates stability of the predicted equilibria. See also Figure 1—figure supplements 1 and 2.

Figure 5 with 1 supplement

Download asset Open asset

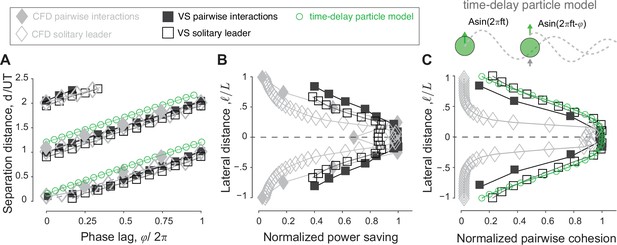
Prediction of energetically beneficial, stable equilibria in the wake of a solitary swimmer at various phase lags and lateral offsets.

(A) Location of maximum $𝕍$ as a function of phase lag $ϕ$ in the wake of solitary leaders in computational fluid dynamics (CFD) and vortex sheet (VS) simulations. For comparison, equilibrium distances of pairwise simulations in CFD, VS, and time-delay particle models (Figure 5—figure supplement 1) are superimposed. Agreement between $𝕍$ -based predictions and actual pairwise equilibria is remarkable. (B) $𝕍$ values also indicate the potential benefits of these equilibria, here shown as a function of lateral distance $ℓ$ for a virtual inphase follower in the wake of a solitary leader in CFD and VS simulations. The power savings of an actual follower in pairwise formations in CFD and VS simulations are superimposed. (C) A negative slope $\partial 𝕋 / \partial d$ of the thrust parameter $𝕋$ indicates stability and $| \partial 𝕋 / \partial d |$ expresses the degree of cohesion of the predicted formations, here, shown as a function of $ℓ$ for an inphase virtual follower. $| \partial F / \partial d |$ obtained from pairwise formations in VS and time-delay particle models are superimposed (Figure 5—figure supplement 1). Results in (B and C) are normalized by the corresponding maximum values to facilitate comparison.

Figure 5—figure supplement 1

Download asset Open asset

Time-delay particle model.

(A) Schematics of time-delayed particle model (Newbolt et al., 2019; Ramananarivo et al., 2016) and its extension to laterally offset swimmers. Each swimmer generates hydrodynamic thrust via oscillating vertically, which also leaves a wake behind it. The follower swimmer interacts with the wake of the leader. (B) For an inphase pair, starting at initial distance $d / U T = 1.15$ , we incrementally increase the lateral offset from $ℓ = 0$ to $ℓ = L$ . (inset) Lateral decay of flow speed in the wake of a solitary swimmer in the vortex sheet model (blue line) and the fitted exponential curve (red line). The lateral exponential decay in the time-delay particle model takes the form $\exp (- | ℓ / 1.6 |^{2.73})$ . (C) The hydrodynamic force $⟨ F_{2} ⟩$ acting on the follower as a function of the corresponding distance from the equilibrium. Due to the decay of the leader’s wake in the lateral direction (see inset in A), the hydrodynamic force $⟨ F_{2} ⟩$ experienced by the follower decreases in magnitude at increasing lateral offset $ℓ$ . Orange lines show the linear change in force at the corresponding equilibria. The slope $δ F / δ d$ is a measure of linear stability. Negative slopes imply stable formations for all $ℓ \leq L$ , but these slopes become more shallow as we increase $ℓ$ .

Figure 6

Download asset Open asset

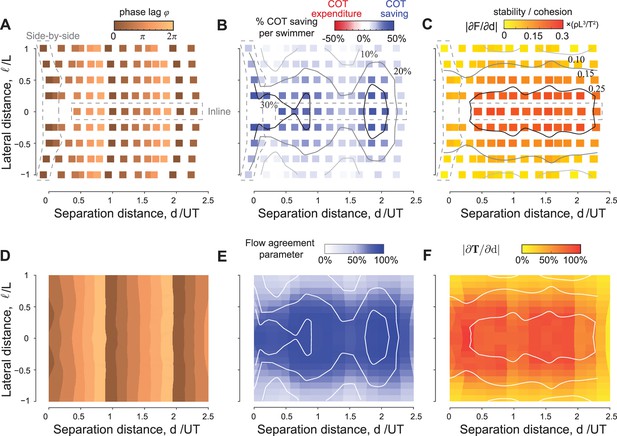
Equilibria are dense over the parameter space of phase lags and lateral offsets.

For any given phase lag $ϕ$ and at any lateral offset $ℓ$ inside the wake, the pair reach equilibrium formations that are stable and power saving relative to a solitary swimmer. (A) Equilibrium separation distances, (B) average power saving, and (C) stability as a function of phase lag and lateral distance in a pair of swimmers. Predictions of (D) equilibrium locations, (E) hydrodynamic benefits, and (F) cohesion based on the wake of a solitary swimmer following the approach in Figures 4 and 5. For comparison, the contour lines from (B and C) based on pairwise interactions are superimposed onto panels (E and F) (white lines). Simulations in (A–C) are based on pairwise interactions and simulations in (D–F) are based on the wake of a single swimmer, all in the context of the vortex sheet model with $A = 15^{\circ}$ , $f = 1$ , and $τ_{diss} = 2.45 T$ .

Figure 7 with 2 supplements

Download asset Open asset

Larger inline and side-by-side formations.

(A) Inline formations lose cohesion and split into two subgroups as depicted here for a group of six swimmers. (B) Side-by-side formations remain cohesive. (C) Power saving of each swimmer in inline and side-by-side formations. Dissipation time $τ_{diss} = 2.45 T$ . Simulations of inline formations and side-by-side formations ranging from two to six swimmers are shown in Figure 7—figure supplements 1 and 2.

Figure 7—figure supplement 1

Download asset Open asset

Inline formations of multiple flapping swimmers.

Snapshots of inline formations composed of 2, 3, 4, 5, and 6 swimmers in vortex sheet (VS) simulations at steady state; time evolution of pairwise distances is shown on the right. (A and B) Formations composed of 2 or 3 swimmers are stable with at consecutive spacing $d / U T = 1$ . (C) For a trail of 4 swimmers, the group splits into a leading subgroup of 3 swimmers while the fourth swimmer separates from the rest. (D and E) For formation of 5 or 6 swimmers, the group splits into a leading subgroup of 3 swimmers and another subgroup containing the remaining 2 or 3 swimmers. (F) reports recent savings in COT for each swimmer and the average of the whole group.

Figure 7—figure supplement 2

Download asset Open asset

Side-by-side formations of multiple flapping swimmers.

Vortex sheet simulation of side-by-side formations with 2 (A), 3 (B), 4 (C), 5 (D), and 6 (E) swimmers, from top to bottom, respectively. On right-hand side, we report pairwise spacing between them. In all of the groups the formations are stable and the distances between every pair are close to zero. (F) reports recent savings in COT for each swimmer and the average of the whole group.

Figure 8

Download asset Open asset

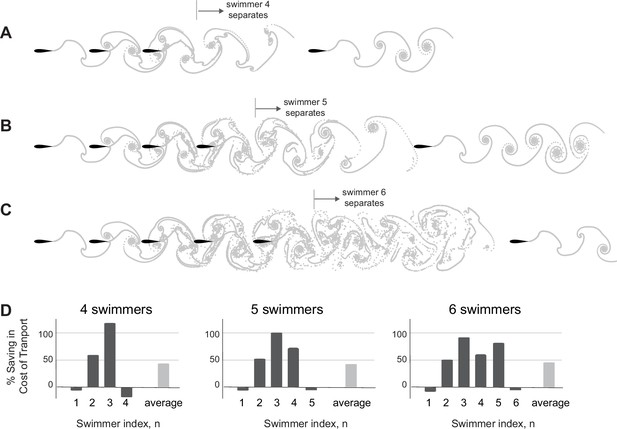
Loss of cohesion in larger groups of inline swimmers.

Number of swimmers that stay in cohesive formation depends on parameter values. (**A–C**) For dissipation time $τ_{diss} = 2.45 T$ , $3.45 T$ , and $4.45 T$ , the fourth, fifth, and sixth swimmers separate from the group, respectively. (D) Power savings per swimmer in (A–C), respectively. On average, all schools save equally in cost of transport, but the distribution of these savings vary significantly between swimmers. In all case, swimmer 3 receives the most hydrodynamic benefits.

Figure 9 with 1 supplement

Download asset Open asset

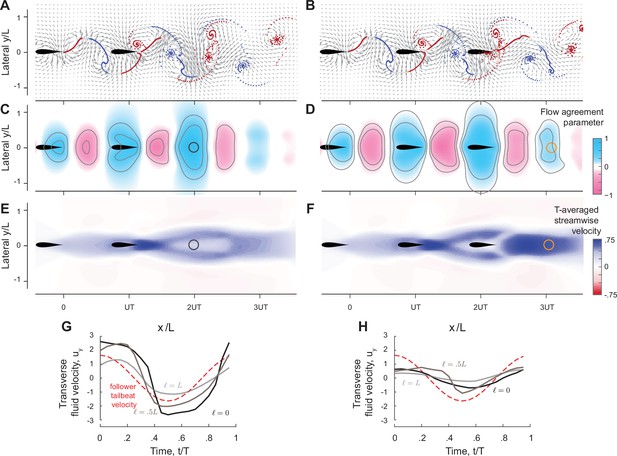
Prediction of equilibrium locations in the wake of multiple upstream swimmers.

(A, B) Snapshots of vorticity fields created by two inline inphase swimmers, and three inline inphase swimmers. (C, D) show the corresponding flow agreement parameter $𝕍$ fields. Contour lines represent flow agreement parameter at ±0.25, ±0.5. (E, F) plot the corresponding period-averaged streamwise velocity. Separation distances $d / U T$ predicted by the locations of maximal $𝕍$ are marked by circles in the flow agreement field. In the left column, separation distances $d / U T$ based on freely swimming triplets are marked by black circles and coincide with the locations of maximal $𝕍$ . In the right column, the orange marker shows the prediction of the location of a fourth swimmer based on the maximum flow agreement parameter. In two-way coupled simulation, swimmer 4 actually separates from the leading three swimmers as illustrated in Figure 8A. Computational fluid dynamics (CFD) simulation shows swimmer 4 will collide with swimmer 3 as in Figure 9—figure supplement 1. (**G, H**) show the transverse flow velocity in a period at the location predicted by the maximum flow agreement parameter and with a lateral offset $ℓ = 0, 0.5 L, L$ , in comparison to the follower’s tailbeat velocity.

Figure 9—figure supplement 1

Download asset Open asset

Inline formations of multiple flapping swimmers in computational fluid dynamics (CFD) simulations.

CFD simulation of inline formations with three (A) and four (B) swimmers at Re=1645. Vorticity field is shown on the left-hand side. On right-hand side, we report pairwise spacing between them. The pitching amplitude of leader and follower is set to $A = 15^{\circ}$ .

Figure 10 with 1 supplement

Download asset Open asset

Passive and active methods for stabilizing an emergent formation of four swimmers.

(A) In an inline school of four swimmers, the leading three swimmers flap inphase, but swimmer 4 actively controls its phase in response to the flow it perceives locally to match its phase to that of the local flow as proposed in Li et al., 2020. The phase controller stabilizes swimmer 4 in formation but at no hydrodynamic benefit. (B) Sequentially increasing the phase lag by a fixed amount $Δ ϕ = - 30^{o}$ in an inline school of four swimmers stabilizes the trailing swimmer but at no hydrodynamic benefit. (C) Gradually tuning the phase lag $Δ ϕ$ in a school of four swimmers as done in (B). At moderate phase lags, the school stays cohesive (top plot) but swimmer 4 barely gets any power savings (bottom plot). (D) By laterally offsetting the swimmers, four swimmers, all flapping inphase, form cohesive schools with different patterns, e.g., with side-by-side pairing of two swimmers, staggered, and diamond patterns. The time evolution of separation distances is shown in Figure 10—figure supplement 1. Individual in each pattern receive a different amount of hydrodynamic benefit. Diamond formation provides the most power saving for the school as anticipated in Weihs, 1973, for a school in a regular infinite lattice. In (A, B, and D), %values indicate the additional saving or expenditure in cost of transport relative to solitary swimming.

Figure 10—figure supplement 1

Download asset Open asset

Alternative formations of four flapping swimmers.

Vortex sheet simulation of four swimmers with alternative formations. On right hand side, we report pairwise spacing between them. The lateral distance is $ℓ = 0.25 L$ . (A) Two leading swimmers swim side by side. The third and forth swimmer collide to each other. (B) The same configuration as in (A) with larger initial distance between the third and forth swimmer. They form a stable school. The forth swimmer stays at the second equilibrium behind the third swimmer. (C) An additional swimmer is placed side by side to the second swimmer in a school of three inline swimmers. The second and third swimmer stays at the second equilibrium from the first swimmer, and the forth swimmer stays at the second equilibrium from the second and third swimmer. (D) An additional swimmer is placed side by side to the third swimmer in a school of three inline swimmers. The last two swimmers stay at the second equilibrium from the second swimmer. (E) Four inline inphase swimmers when initially placed close to the second equilibrium. Power saving per swimmer is reported in Figure 10.

Author response image 1

Download asset Open asset

Antiphase self-propelled anguilliform swimmers.

(a) – (d) Wavelet adapted vorticity fields at, respectively, t = T, t = 4T, t = 10T. (e) Absolute normalized velocities |U|/L. (f) Swimmers’ centre of mass trajectories.

Author response image 2

Download asset Open asset

Parallel schooling formation.

(a) – (d) wavelet adapted vorticity fields at, respectively, t = T, t = 4T, t = 7T, t = 10T. (e) Absolute normalized velocities |U|/L. (f) Swimmers’ center of mass trajectories.

Author response image 3

Download asset Open asset

Author response image 4

Download asset Open asset

Videos

Video 1

Download asset

posterframe for video — Pairs of flow-coupled swimmers self-organize into stable inline, staggered, or side-by-side formation.

Energetic benefits depend on the spatial pattern. Results based on flapping foils in computational fluid dynamics (CFD) simulations.

Video 2

Download asset

Tables

Table 1

Data collection from published literature.

We calculated the Reynolds numbers based on swimming speed ( ${R e}_{U} = ρ U L / μ$ ) and flapping velocity ( ${R e}_{A} = 2 π ρ A f L / μ$ ), where $f = 1 / T$ is the flapping frequency. Missing values are either not applicable or not available.

Reference	Study type	System	Distance	Phase	Re_U	Re_A
Kim et al., 2010	Numerical	Flapping flags	Head-to-head	$ϕ \in [0, 2 π]$	200 –400	–
Zhu et al., 2014	Numerical	Heaving flexible foils	–	$ϕ \in [0, π]$	500	200
Ramananarivo et al., 2016	Experimental	Heaving foils	Tail-to-head	$ϕ = 0$	10³ –10⁴	10² –10³
Peng et al., 2018	Numerical	Heaving flexible foils	Tail-to-head	$ϕ = 0$	509	200
Newbolt et al., 2019	Experimental	Heaving foils	Tail-to-head	$ϕ \in [0, 2 π]$	10³ –10⁴	10² –10³
Li et al., 2020	Experimental	Goldfish	Head-to-head	$ϕ \in [0, 2 π]$	10⁵	10⁴
Kurt et al., 2021	Experimental	Pitching foils	Tail-to-head	$ϕ \in [0, 2 π]$	9950	18,850
Heydari and Kanso, 2021	Numerical	Heaving plates	Tail-to-head	$ϕ = 0$	–	–
		Pitching plates	Head-to-head	$ϕ = 0$	–	–
Arranz et al., 2022	Numerical	Heaving flexible foils (3D)	Tail-to-head	$ϕ \in [0, 2 π]$	176	200
Thandiackal and Lauder, 2023	Experimental	Fish-foil interactions	Tail-to-head	$ϕ \in [0, 2 π]$	20·10³ (foil)	50·10³ (foil)
					40·10³ (fish)
Becker et al., 2015 *	Experimental	Heaving foils	Tail-to-head	$ϕ = 0$ , $π$	–	10² –10⁴
Park and Sung, 2018 *	Numerical	Heaving flexible foils	–	$ϕ \in [0, 2 π]$	60 –1100	100 –1200
Dai et al., 2018 *	Numerical	Pitching + heaving foils	–	$ϕ = 0$ , $π$	440	600

*

Data not included in Figure 3.

Additional files

MDAR checklist: https://cdn.elifesciences.org/articles/96129/elife-96129-mdarchecklist1-v1.pdf
Download elife-96129-mdarchecklist1-v1.pdf

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Sina Heydari
Haotian Hang
Eva Kanso

(2024)

Mapping spatial patterns to energetic benefits in groups of flow-coupled swimmers

eLife 13:RP96129.

https://doi.org/10.7554/eLife.96129.3

Figures

Flow-coupled swimmers self-organize into stable pairwise formations.

Computational fluid dynamics (CFD) simulations of pairwise formations.

Vortex sheet (VS) simulations of pairwise formations.

Computational fluid dynamics (CFD) and vortex sheet (VS) simulations at various flow properties.

Hydrodynamic moment acting on pairs of flapping swimmers.

Emergent equilibria in pairwise formations.

Hydrodynamic benefits and linear phase-distance relationship in pairwise formations.

Prediction of relative equilibria in the wake of a solitary swimmer.

Prediction of energetically beneficial, stable equilibria in the wake of a solitary swimmer at various phase lags and lateral offsets.

Time-delay particle model.

Equilibria are dense over the parameter space of phase lags and lateral offsets.

Larger inline and side-by-side formations.

Inline formations of multiple flapping swimmers.

Side-by-side formations of multiple flapping swimmers.

Loss of cohesion in larger groups of inline swimmers.

Prediction of equilibrium locations in the wake of multiple upstream swimmers.

Inline formations of multiple flapping swimmers in computational fluid dynamics (CFD) simulations.

Passive and active methods for stabilizing an emergent formation of four swimmers.

Alternative formations of four flapping swimmers.

Antiphase self-propelled anguilliform swimmers.

Parallel schooling formation.

Videos

Pairs of flow-coupled swimmers self-organize into stable inline, staggered, or side-by-side formation.

Groups of flow-coupled swimmers self-organize into inline, side-by-side, or staggered patterns of distinct cohesion and energy-saving properties.

Tables

Data collection from published literature.

Additional files

MDAR checklist

Download links

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Be the first to read new articles from eLife

Share this article

Cite this article

Flow-coupled swimmers self-organize into stable pairwise formations.

Computational fluid dynamics (CFD) simulations of pairwise formations.

Vortex sheet (VS) simulations of pairwise formations.

Computational fluid dynamics (CFD) and vortex sheet (VS) simulations at various flow properties.

Hydrodynamic moment acting on pairs of flapping swimmers.

Emergent equilibria in pairwise formations.

Hydrodynamic benefits and linear phase-distance relationship in pairwise formations.

Prediction of relative equilibria in the wake of a solitary swimmer.

Prediction of energetically beneficial, stable equilibria in the wake of a solitary swimmer at various phase lags and lateral offsets.

Time-delay particle model.

Equilibria are dense over the parameter space of phase lags and lateral offsets.

Larger inline and side-by-side formations.

Inline formations of multiple flapping swimmers.

Side-by-side formations of multiple flapping swimmers.

Loss of cohesion in larger groups of inline swimmers.

Prediction of equilibrium locations in the wake of multiple upstream swimmers.

Inline formations of multiple flapping swimmers in computational fluid dynamics (CFD) simulations.

Passive and active methods for stabilizing an emergent formation of four swimmers.

Alternative formations of four flapping swimmers.

Antiphase self-propelled anguilliform swimmers.

Parallel schooling formation.

Pairs of flow-coupled swimmers self-organize into stable inline, staggered, or side-by-side formation.

Groups of flow-coupled swimmers self-organize into inline, side-by-side, or staggered patterns of distinct cohesion and energy-saving properties.

Data collection from published literature.

MDAR checklist

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)