Spatial periodicity in grid cell firing is explained by a neural sequence code of 2-D trajectories
- Department of Mathematical Sciences, George Mason University, United States
- Department of Bioengineering, George Mason University, United States
Figures
Figure 1 with 1 supplement
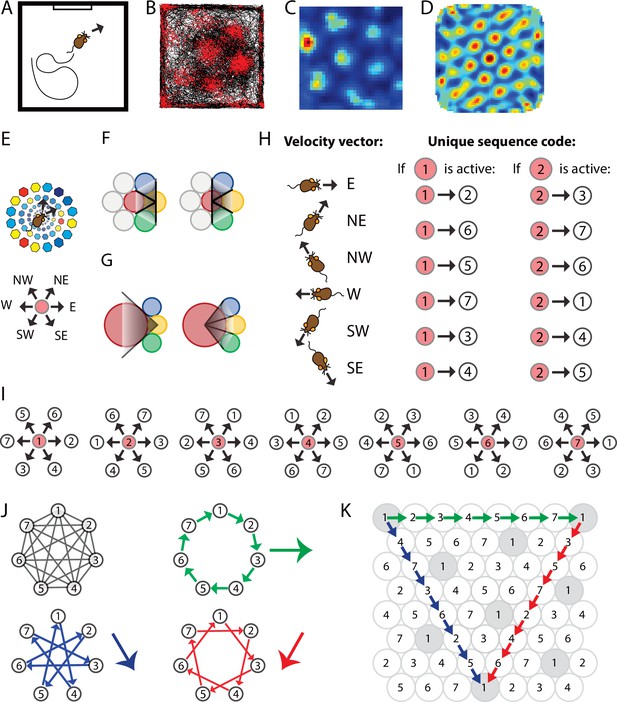
Spatially periodic firing of grid cells in 2-D space emerges from a neural sequence code of trajectories.
(A) Schematic drawing of a 1 × 1 m2 environment surrounded by walls in the presence of a single visual cue card. (B) Trajectory plot visualizing grid cell spiking activity as a function of the animal’s location in space. Data obtained from the medial entorhinal cortex of a freely foraging mouse (Dannenberg et al., 2020; Dannenberg et al., 2019). The black line indicates the path taken by the animal. Red dots indicate the locations where action potentials (spikes) were generated by the grid cell. (C) Firing rate map of the spiking data shown in (A). Data are visualized as 3 × 3 cm2 spatial bins, smoothed with a Gaussian kernel. Red and blue colors indicate high and low firing rates. Peak and average firing rates are 15 and 1.9 Hz. (D) Spatial autocorrelogram of the data shown in (B). Red and blue colors indicate high and low correlation values. (E) The animal’s current position and velocity determine the animal’s trajectory. In a sequence code, directions are represented by pairs of sequentially active cell assemblies with non-overlapping cellular composition. We refer to the individual members in a set of completely distinct cell assemblies as elements. The red circle represents the currently active element. The next active element in the sequence code is uniquely determined by the currently active cell and the velocity vector (Definition 8). N = north, NE = northeast, NW = northwest, W = west, SW = southwest, and SE = southeast. (F) Elements’ firing fields that surround each other symmetrically in a hexagonal lattice packing allow for equal angular resolution in the coding of trajectories by cell sequences. Colors represent distinct elements. (G) If an element’s firing field was surrounded by fewer or more than six firing fields that touched each other, opposite directions would not be represented at the same angular resolution. In this example, east → west cannot be distinguished from east → northwest and east → southwest because the three directions are represented by the same sequence of elements, yellow → red. However, the opposite direction, west → east, is represented by three different cell sequences allowing for a finer angular resolution in the representation of traveling direction. (H) Example of possible pairs of elements creating a sequence code. If the sequence code shall represent all directions with equal angular resolution, the cellular composition of sequentially active cell assemblies needs to be completely distinct every 60° (E, F). Possible representations of velocity vectors by sequences of two elements are shown for when the currently active element is #1 or #2. Numbers within circles identify distinct elements. (I) Example of a complete sequence code that uniquely represents all directions at 60° resolution as a function of the currently active element and the traveling direction. (J) Sequential activation of seven distinct elements can code for infinitely long trajectories along all three major axes of a hexagonal lattice. (K) The same sequential activation map as in (I) and (J) but plotted in 2-D space. Note that the firing fields of individual elements form grid maps in 2-D space, as highlighted in gray for element #1.
Figure 1—figure supplement 1
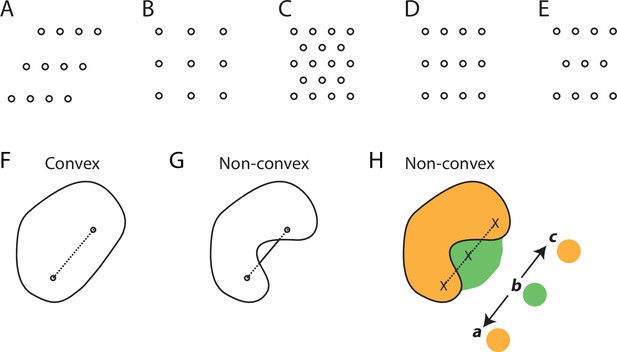
Trajectory coding by cell sequences requires a dense packing of convex firing fields.
(A–E) Examples of the five types of lattices in the plane. (A) Oblique. (B) Square. (C) Hexagonal. (D) Rectangular. (E) Centered rectangular. (F, G) Examples of a convex and non-convex geometric object such as a possible spatial firing field of a neuron. (H) A non-convex spatial firing field that results in an ambiguous cell sequence code for trajectories in space. In this example, two spatial firing fields of two cells are shown, indicated by green and orange colors. The three crosses mark three locations in space. The sequence green → orange can represent two opposite trajectories, namely b → a and b → c.
Figure 2
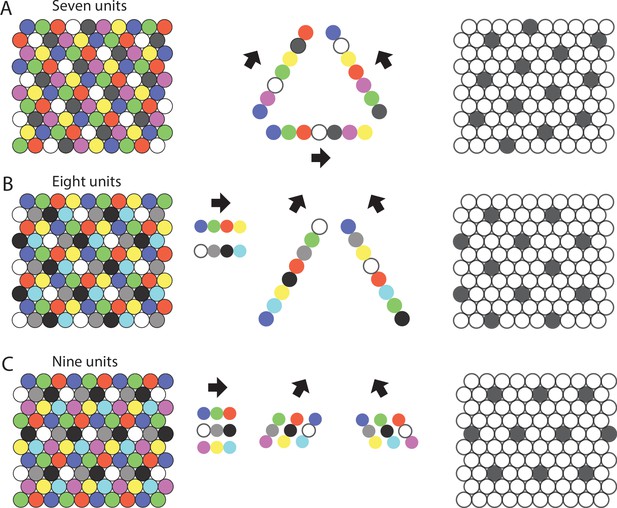
Repeating sequences of elements coding for trajectories result in lattice packing of firing fields.
Left panels show firing fields of multiple distinct elements with non-overlapping firing fields arranged in a 2-D lattice packing (grid). Each grid provides a sequence code of trajectories. Mid panels show the sequences that code for the directions along the three major axes of the grid. Right panels highlight the firing fields of an individual element visualizing the type of lattice formed by the firing fields of one element. (A) An example of the minimal number of seven elements and resulting sequences with repeat length 7 along the three grid axes. The resulting firing fields of individual elements (referred to as a ‘grid map’ in animal experiments) are arranged on a hexagonal lattice rotated by 10.9° against a vertical axis. (B) An example of eight cells and sequences with repeat lengths 4 along one axis, and repeat length 8 along the two other axes. The resulting firing fields are arranged on a centered rectangular lattice. (C) An example of nine cells and sequences with repeat length 3 along all three grid axes, resulting in hexagonal lattice packing of individual elements’ firing fields.
Figure 3 with 2 supplements
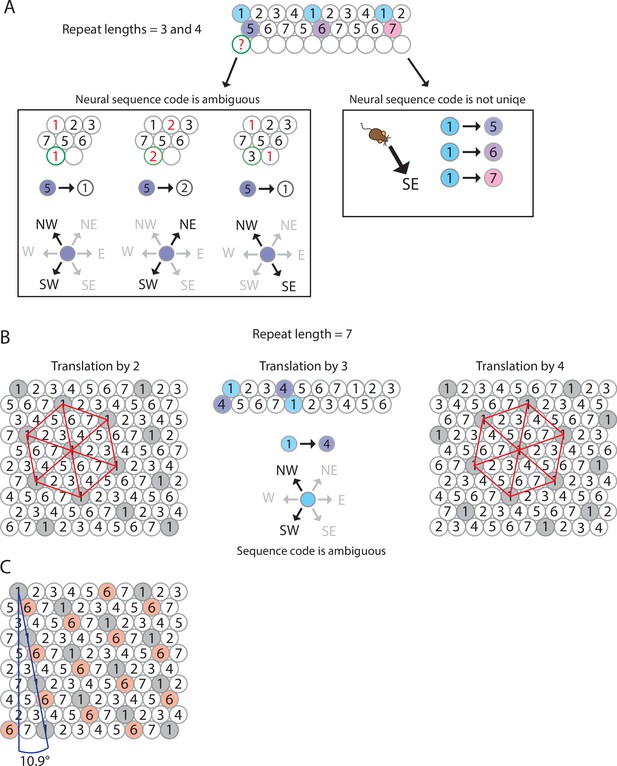
The minimum number of distinct elements providing a sequence code of trajectories in 2-D space is 7, and there are exactly 2 possible arrangements of elements up to relabeling.
(A) Repeat lengths that are smaller than 7 result in a violation of a sequence code of trajectories because the code would be ambiguous and not unique. A red question mark indicates that no element can be found for this position that would not violate the sequence code. Red numbers indicate that activity of this element at the current position would violate sequence coding of trajectories due to ambiguity. Blue background color marks the sequential activity of two elements that violate the sequence code of trajectories (Definition 8) because the next active cell in the sequence is not uniquely determined by the currently active cell and the velocity vector associated with the current trajectory of an animal. (B) If the repeat length is 7, there are three potential translations of the sequence in row 1 to fill up row 2 (see Mathematical proof). Only two of those three translations result in an arrangement of elements (up to relabeling of elements) that creates a sequence code for trajectories in 2-D space. These two arrangements are mirror images of each other and imply that the firing fields of each individual grid element fall on the vertices of equilateral triangles, i.e., they form a hexagonal grid. (C) Both possible arrangements of firing fields imply that grid patterns of other grid elements have the same spacing and rotation, and only differ in spatial phase (compare grid patterns of element #1 and element #6). The smallest angle between one grid axis and the boundary of a rectangular enclosure is 10.9° if one row of sequences is aligned with one of the borders of the enclosure.
Figure 3—figure supplement 1
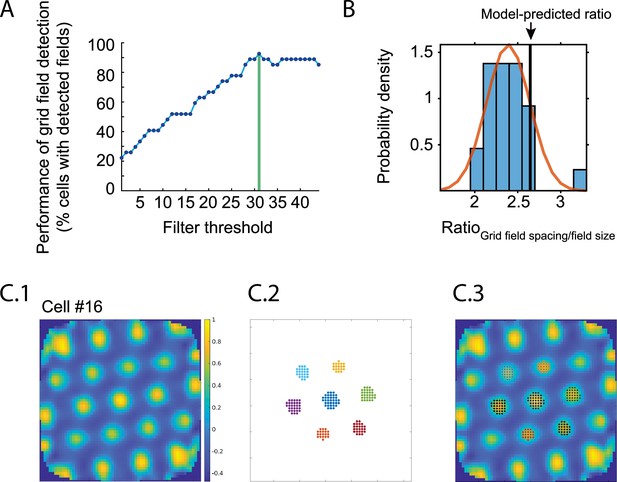
Quantification of grid field spacing and grid field size in grid cells obtained from mice.
We analyzed a total of 27 grid cells from a previously published study (Gleeson et al., 2017) to quantify the ratio between grid field spacing and grid field size. The experimental data on grid cells were obtained from mice freely foraging in a 1 × 1 m2 square environment with walls and a visual cue card during baseline recording sessions. The model-predicted value of the ratio of grid field spacing to a diameter-like metric of field size is √7 ≈ 2.65. Note that this reflects the ideal ratio assuming no noise in experimental measurements, no transient drifts of grid maps, no path integration error, no conjunctive coding or any other factors that could result in out-of-field firing of recorded neurons. The grid field size measured from firing rate maps of experimental data is, therefore, expected to be larger than the model-predicted grid field size, resulting in smaller ratios of grid field spacing/field size. (A) Successful identification of grid fields for quantification of grid field size is a function of the applied filter threshold (see ‘Methods’). The algorithm performed best (measured as the percentage of cells where grid fields could be detected) with a filter threshold of 31% of the peak firing rate (vertical green line). (B) Histogram of the ratios measured in n = 25 grid cells out of 27 grid cells, obtained with applying the 31% filter threshold. As expected, the model-predicted value is larger but falls within the distribution of experimental data with mean = 2.44 and standard deviation = 0.23. The red line shows a normal distribution with the experimentally observed mean and standard deviation. (C) Performance of the grid field detection algorithm illustrated for one example neuron (cell #16). (C.1) The spatial autocorrelogram of the firing rate map of cell #16. (C.2) Grid fields detected by the field detection algorithm with the filter threshold set to 31% of the peak firing rate. Colors identify individual grid fields. The measured ratio (grid field spacing/field size) of this cell was 2.48. (C.3) Detected grid fields merged with spatial autocorrelogram.
Figure 3—figure supplement 2
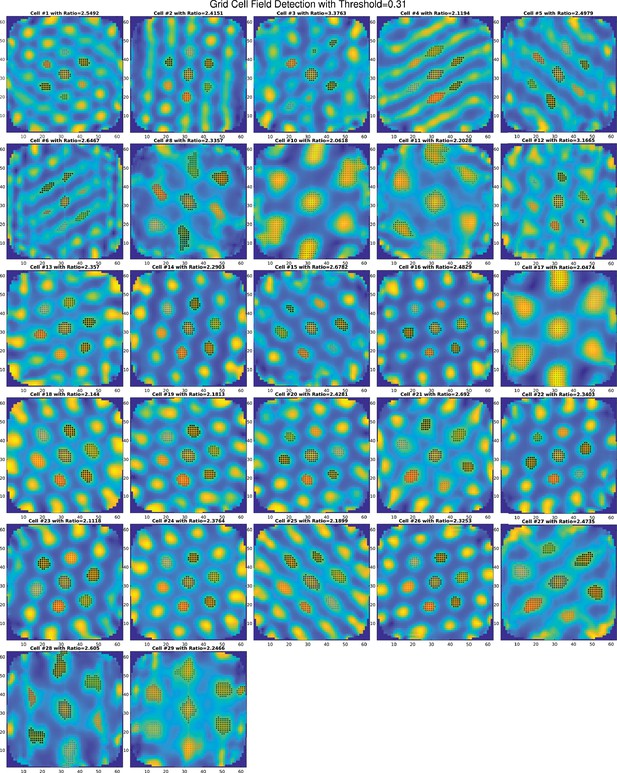
Grid field detection with filter threshold set to 31% of the peak firing rate.
Data show the grid field detection performance for all n = 27 grid cells recorded under baseline conditions from Dannenberg et al., 2020. Grid field detection failed for cells #3 and #29. Cells #7 and #9 were not classified as grid cells during baseline recording sessions and, therefore, excluded for this analysis.
Figure 4
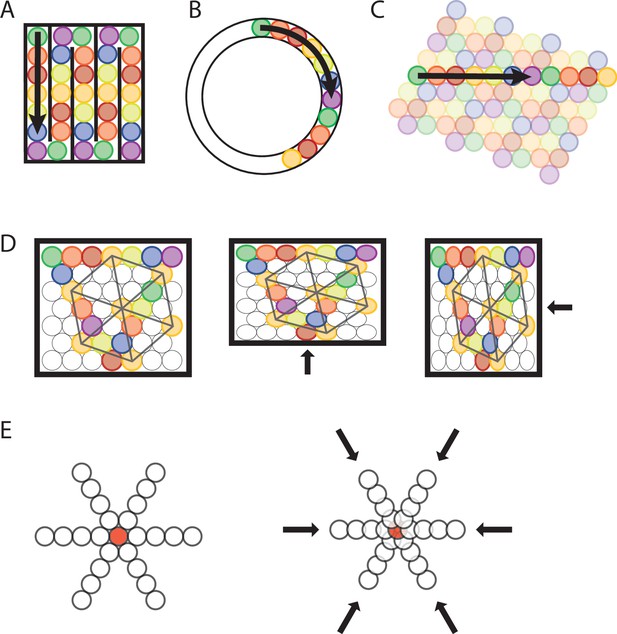
Transformation of a sequence code of trajectories from 2-D space to 1D space.
(A, B) A sequence of seven different elements can code for a trajectory in a 1-D compartmentalized ‘hairpin’ maze (A) or a 1-D circular track (B). Note that the distance between firing fields would increase in the 1-D ‘hairpin’ maze and 1-D circular track compared to the distance between spatial firing fields in a 2-D environment. Also note that sequences could undergo a phase reset at behaviorally relevant points, for example, the turning points in the ‘hairpin’ maze (A). (C) The sequence of active elements in a 1-D environment can be interpreted as a cross-section of the trajectory sequence code in a 2-D space. (D) Anchoring of firing fields to environmental borders predicts parametric rescaling of an individual element’s grid pattern when a familiar enclosure is deformed. Each color represents one grid element, each circle represents one firing field. For clarity, the complete set of firing fields of an individual element is shown only for one element (orange color). In addition, sequences are shown for all three major axes. Left panel, original maze configuration. Mid and right panel, the environment is compressed along the vertical or horizontal dimension resulting in a parametric deformation of firing fields and the grid pattern of individual elements’ firing fields along the vertical or horizontal dimension. (E) Progressively faster advancement from the currently active element to the next active element in the sequence code of trajectories results in progressive decrease in grid spacing and thereby a local distortion of the grid map. Open circles represent firing fields of grid elements along the three major axes. The red-filled circle in the center represents a salient location such as a rewarded goal location toward which nearby grid fields gravitate.
Figure 5 with 1 supplement
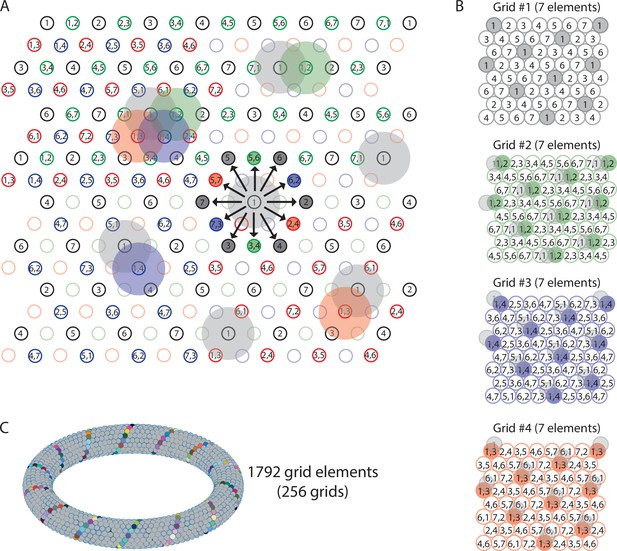
Multiple grids provide nearly continuous resolution in the coding of trajectories.
(A) The circles with numbers show the centers of the grid fields from four grids, each composed of seven distinct elements (total of 28 grid elements). Shaded areas represent the firing fields of individual elements. Elements with non-overlapping firing fields form ‘grids’, shown in black, green, blue, and red colors. Each number within a circle identifies a distinct element. If elements represent cell assemblies, a combination of numbers (e.g., ‘1,2’) identifies an element whose cellular composition is an overlap between two elements with adjacent firing fields. For example, element ‘1,2’ is composed of cells that are part of elements ‘1’ and ‘2’, resulting in an overlap of firing fields. For visual clarity, not all element numbers are shown. (B) Grids #2, #3, and #4 are phase-shifted along one of the three major axes of grid #1. The emerging grid map of an individual element’s firing fields is highlighted in color for one grid element in each grid. The phase-shift of each grid is indicated by showing the transparent grid pattern of grid #1. (C) When more grid elements are added, the elements can be represented in 3D neural space as a neural manifold, shown here for a total of 1792 grid elements forming 256 grids of non-overlapping firing fields. The colored cells represent one diagonal axis across rows of non-repeating elements if plotted in the 2-D plane as shown in (A).
Figure 5—figure supplement 1
Grid cell modules provide a pyramidal parametric sampling of 2-D space enabling simultaneous multiscale representation of space.
The sampling of 2-D space by grid fields is cut in half from module to module so that each grid cell module represents space at half of the resolution of the previous module. This resembles Gaussian pyramids or mip maps in computer vision. Representation of 2-D space by different grid cell modules thereby allows the simultaneous representation of space at meaningful spatial resolutions in a computationally efficient way. The blue box represents a 1-m × 1-m square environment. Circles represent densely packed grid fields from multiple grid cells. Filled circles represent grid fields of a single grid cell. Grid fields are enlarged in space from module to module so that the total number of grid fields sampling the space approximately doubles from module to module. While the total number of grid fields doubles from module to module, the spacing between the grid fields of an individual grid cell increases by a factor of √2.
Author response image 1
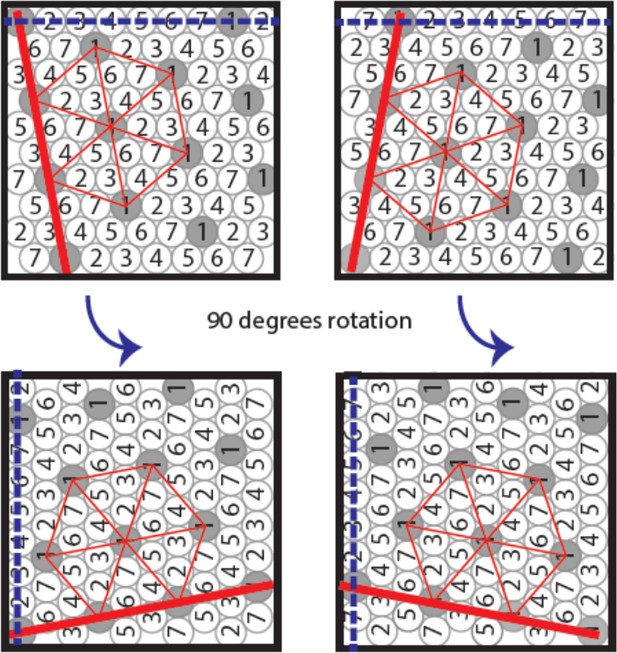
Under the premise that a sequence of firing fields aligns with one of the geometric boundaries (walls) of a square arena, there are precisely four possible distinct configurations of orientations.
This is precisely what has been observed in experiments (Stensola et al., 2015; Stensola and Moser, 2016).
Videos
Video 1
Local path integration in a sequence code of trajectories begets hexagonal firing of grid cells.
Tables
Table 1
Axioms from which grid cell firing emerges as the most parsimonious solution to provide a code for trajectories in 2-D space.
| Axiom | Remark/example | |
|---|---|---|
| Axiom 1 | Cell sequences code for trajectories in 2-D space | This axiom states that the sequential activity of two cells, e.g., i → j, can unambiguously be interpreted by a downstream reader mechanism as a code for one and only one trajectory, e.g., moving from place A to place B |
| Axiom 2 | The reverse cell sequence codes for the reverse trajectory | If the cell sequence i → j codes for moving from place A to B, then the reverse cell sequence j → i codes for moving from place B to place A |
| Axiom 3 | Each cell’s firing field is surrounded symmetrically by other cell’s firing fields so that the angular resolution is constant and maximal across all directions | This axiom means that a sequence code should represent each direction equally with no ‘gaps’ in the representation (Figure 3D and E) |
| Axiom 4 | The number of cells is finite | Grid cells are densest in layer II of the medial entorhinal cortex (Sargolini et al., 2006), and this layer has been estimated to contain 24,000 and 58,000 neurons in mice and rats, respectively (Gatome et al., 2010) |
Table 2
List of possible grid maps and properties of these grid maps given the total number of elements participating in a trajectory-coding sequence in a rectangular environment.
For each individual element’s grid map that has a non-zero angle to a border, a reflection or 90° rotation and reflection up to relabeling of the elements exist, and these additional possibilities are not included in this list.
| # cells | Repeat lengths* | Lattice type | Smallest angle to a border of a rectangular environment† |
|---|---|---|---|
| 7 | 7, 7, 7 | Hexagonal | 10.9° |
| 8 | 4, 8, 8 | Centered rectangular | 0° |
| 4, 8, 8 | Oblique | 10.9° | |
| 9 | 3, 3, 3 | Hexagonal | 0° |
| 3, 9, 9 | Oblique | 10.9° | |
| 3, 9, 9 | Oblique | 13.9° | |
| 3, 9, 9 | Oblique | 16.1° | |
| 10 | 5, 10, 10 | Oblique | 0° |
| 5, 10, 10 | Oblique | 10.9° | |
| 5, 10, 10 | Oblique | 16.1° | |
| 11 | 11, 11, 11 | Oblique | 6.6° |
| 11, 11, 11 | Oblique | 10.9° | |
| 11, 11, 11 | Oblique | 16.1° | |
| 12 | 6, 6, 6 | Hexagonal | 0° |
| 3, 12, 12 | Rectangular | 0° | |
| 3, 12, 12 | Rectangular | 10.9° | |
| 3, 4, 12 | Oblique | 0° | |
| 3, 4, 12 | Oblique | 13.9° | |
| 4, 6, 12 | Oblique | 0° | |
| 4, 6, 12 | Oblique | 6.6° | |
| 4, 6, 12 | Oblique | 23.4° |
-
*
Repeat lengths across the three major axes of the hexagonal lattice structure of densely packed firing fields.
-
†
The smallest angle to a border of a rectangular environment assumes that one sequence of elements is arranged in parallel to one wall.
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Software, algorithm | MATLAB | The MathWorks | RRID:SCR_001622; version: 2021a | |
| Software, algorithm | Repository: GitHub; reference: this paper | https://github.com/dannenberglab/grid-cell-sequences/blob/main/get_gridMaps.m copy archived at Dannenberg, 2025 | MATLAB code to plot grid maps that emerge because of sequence coding of trajectories | |
| Software, algorithm | Repository: GitHub; reference: this paper | https://github.com/dannenberglab/grid-cell-sequences/blob/main/plot_torus.m copy archived at Dannenberg, 2025 | MATLAB code to plot toroidal manifold of neural grid cell space from multiple grid units (related to Figure 5C) | |
| Software, algorithm | Repository: GitHub; reference: this paper | https://github.com/Hippocampome-Org/gridcell_metrics | MATLAB code to quantify grid field spacing and grid field size from experimental data on grid cells |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Spatial periodicity in grid cell firing is explained by a neural sequence code of 2-D trajectories
eLife 13:RP96627.
https://doi.org/10.7554/eLife.96627.3
