Implicit motor adaptation patterns in a redundant motor task manipulating a stick with both hands
- Graduate School of Education, The University of Tokyo, Japan
- Japan Society for the Promotion of Science, Japan
Figures
Figure 1
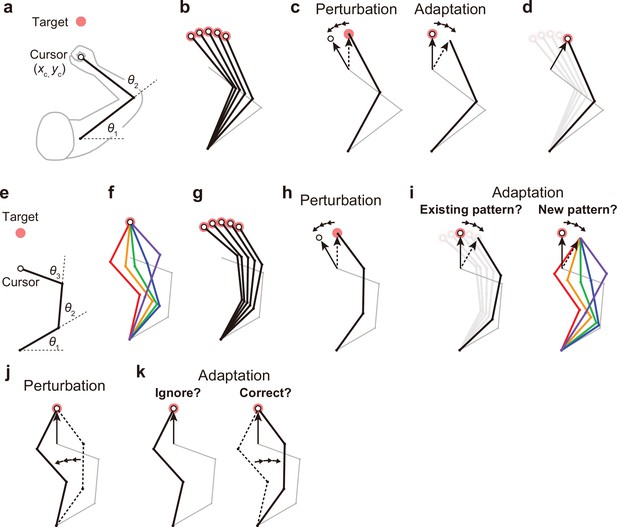
Kinematic redundancy and adaptation patterns.
(a) In the ordinary planar arm-reaching task which primarily uses elbow and shoulder joints, there is no redundancy between the task goal (xc, yc) and the joint angles (θ1, θ2). (b) The movement pattern at each target is determined by the joint angles. (c) The adaptation patterns to a visual rotation are also determined. (d) This adapted joint angle pattern should be identical to that of voluntary reaching in the adapted direction. (e, f) In the case of planar reaching movement by a hypothetical limb with three joints (θ1, θ2, θ3), the cursor can reach the target in a large number of patterns. (g) Given that the motor system solves the task redundancy by optimization, we should observe a stereotypical pattern of joint angles according to the targets. (h, i) The question is whether, when a visual rotation is imposed on the cursor (end-effector relevant perturbation), the motor system adopts the same joint movement pattern as when voluntarily aiming in the adapted direction (left) or a new joint movement pattern (right). (j) The joint angles can be perturbed while the cursor position remains unchanged (end-effector irrelevant perturbation). (k) This perturbation can be ignored because it does not affect the cursor (left). Alternatively, the joint angles may be corrected (right).
Figure 2
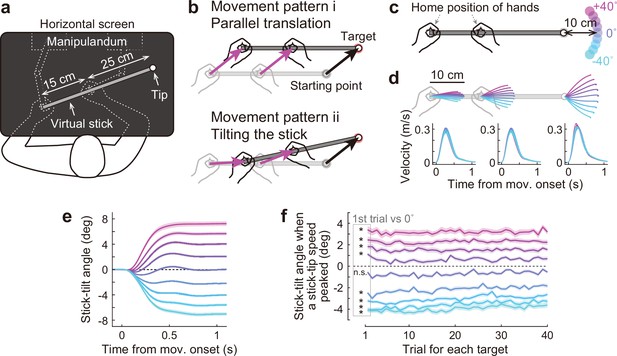
Bimanual stick manipulation task.
(a) Participants held handles of a manipulandum with both hands and moved the right tip of a virtual stick on the monitor. (b) In this task, there are countless movement patterns to move the tip to the target. Two representative strategies are shown: parallel translation (top) and tilting the stick (bottom). (c) During the baseline phase, 72 participants were instructed to move the tip from a starting point to a target that appeared in one of nine directions. (d) Movement trajectories (top) and velocity profiles (bottom) of the left hand, right hand, and tip averaged across participants. Each color corresponds to the target direction shown in c. The shaded areas represent the SEM across participants. (e) The time-course of the stick-tilt angle shows that participants moved the tip while tilting the stick. The shaded areas indicate the SEM. (f) Trial-to-trial changes in stick-tilt angle at the peak velocity of the tip. The strategy of tilting the stick was observed from the beginning of the experiment (t-test compared with zero, |t(71)|>6.4, Bonferroni corrected p<0.001). The shaded areas indicate the SEM.
Figure 3
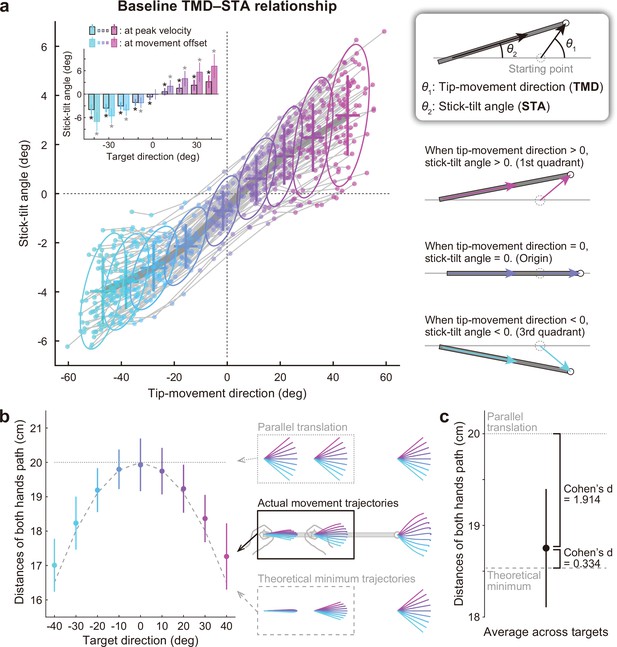
Relationship between the tip-movement direction and stick-tilt angle.
(a) A relationship between each individual’s tip-movement direction and stick-tilt angle, when the tip speed peaked is represented as the thin gray lines drawn with colored plots (N=72 participants). The averaged relationship is plotted as a bold gray line (baseline TMD–STA relationship) with the SD (crosses) and 95% confidence intervals (ellipses). The inset shows the stick-tilt angles at peak velocity and movement offset (error bars: SD, *: t-test compared with 0°, Bonferroni-corrected p<0.01). The monotonically increasing curve indicates the stereotypical strategy of manipulating the stick (diagrams on the right side). (b) Sum of the distances between the initial and final positions of both hands (i.e. the sum of the lengths of pink arrows in Figure 2b). The dotted and dashed gray lines indicate the distances when both hands are moved in parallel and the mathematically derived minimum distances by tilting the stick, respectively. The error bars denote the SD. (c) The distance averaged across target directions was closer to the minimum value (Cohen’s d=1.914) than the parallel translation distance (Cohen’s d=0.334). The error bar indicates the SD across participants.
Figure 4
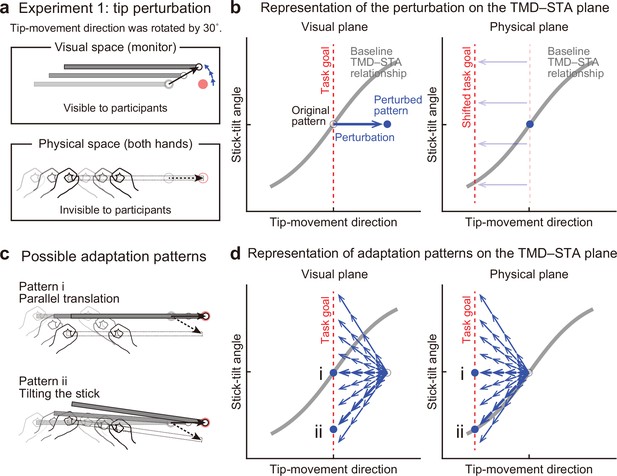
Experiment 1: End-effector relevant visual perturbations.
(a) During the adaptation phase of Experiment 1, the tip-movement direction was rotated by 30° around the starting point (tip perturbation). The dotted and solid black arrows indicate the intended and actual tip trajectory, respectively. (b) The changes in the movement pattern are expressed as the state shift on the plane represented by mapping between tip-movement direction and stick-tilt angle (left: visual space, right: physical space). The dashed red lines denote the task goal (i.e. a target direction). On the visual plane, the perturbation (a blue arrow) shifts the movement pattern. On the physical plane, the task goal is shifted. (c) The participants could correct the tip error without (pattern i, top) or by (pattern ii, bottom) altering the stick-tilt angle. (d) The adaptive strategies are expressed as the shift on the visual plane (left) and the physical plane (right). The visual error caused by the perturbation could be compensated by different adaptation patterns (blue arrows): Representative patterns are expressed as bold arrows (patterns i and ii).
Figure 5 with 3 supplements
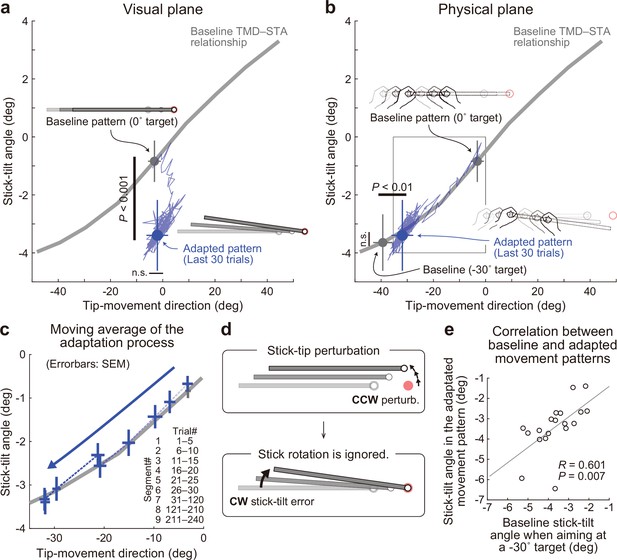
Experiment 1: Adaptation patterns to gradually imposed end-effector relevant perturbations.
(a) In Experiment1A (N=19 participants), the adaptation trajectory (a thin blue line) on the visual plane gradually deviated from a baseline pattern (a gray circle) mainly along the y-axis. The tip-movement direction remained at the baseline level (paired t-test, t(18) = –1.320, p=0.203). In contrast, the stick-tilt angle after the adaptation (a blue circle) significantly differed from that in the baseline pattern when aiming at the 0° target (a gray circle; paired t-tests, t(18) = 10.003, p<0.001), indicating that the participants saw the abnormal visual stick-tilt. The plots indicate mean ± SD across participants. (b) On the physical plane, the adaptation trajectory followed the baseline TMD–STA relationship. Although the difference was small but significant for the tip-movement direction compared with the baseline pattern when aiming at the –30° target (paired t-test, t(18) = –10.053, p<0.01), there was no significant difference in the stick-tilt angle (paired t-test, t(18) = –1.081, p=0.294). (c) The area indicated by the squared outline in b is enlarged. The adaptive process can be divided into nine trial segments (trials 1–5, 6–10, 11–15, 16–20, 21–25, 26–30, 30–120, 121–210, and 211–240). (d) The motor system implicitly achieved adaptation to the tip perturbation as if it had voluntarily aimed at the –30° target. (e) Participants who showed a larger stick-tilt when aiming at the –30° target during the baseline phase also exhibited a larger stick-tilt in the adapted pattern (R=0.601, p<0.007).
Figure 5—figure supplement 1
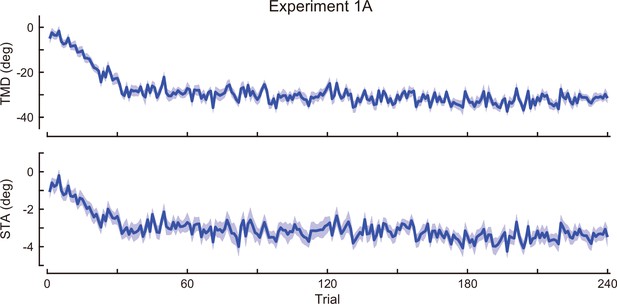
Time-course of the movement pattern in the adaptation phase.
Changes in the movement pattern in the physical space are shown (the tip-movement direction (top) and stick-tilt angle (bottom)). The data shows mean ± SEM across participants (N=19 participants).
Figure 5—figure supplement 2
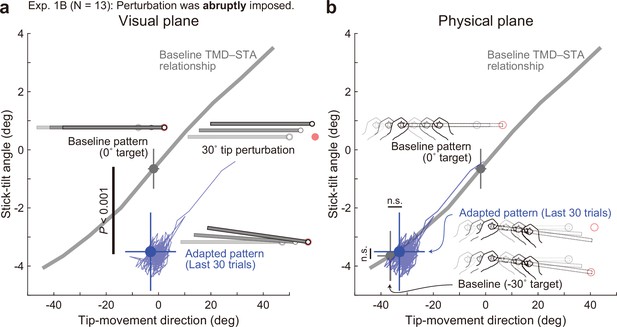
Adaptation patterns to abruptly imposed end-effector relevant perturbations.
(a) In Experiment 1B (N=13 participants), a 30° tip perturbation was applied from the first trial of the adaptation phase. On the visual plane, the stick-tilt angle after the adaptation (a blue circle) significantly differed from that in the baseline pattern when aiming at the 0° target (a gray circle) (paired t-tests, t(12) = 7.529, p<0.001), whereas the tip-movement direction remained at the baseline level (paired t-test, t(12) = 0.430, p=0.675). The formats are the same as Figure 5a. (b) On the physical plane, neither tip-movement direction nor stick-tilt angle in the adapted pattern was significantly different from that in the baseline pattern when aiming at the –30° target (paired t-test, TMD: t(12) = –1.628, p=0.129, STA: t(12) = –0.490, p=0.633).
Figure 5—figure supplement 3
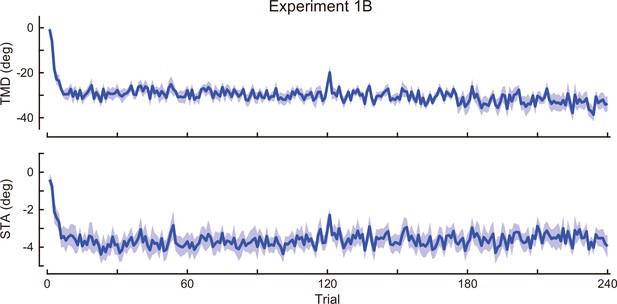
Time-course of the movement pattern in the adaptation phase.
Changes in the movement pattern in the physical space are shown (the tip-movement direction (top) and stick-tilt angle (bottom)). The data shows mean ± SEM across participants (N=13 participants).
Figure 6
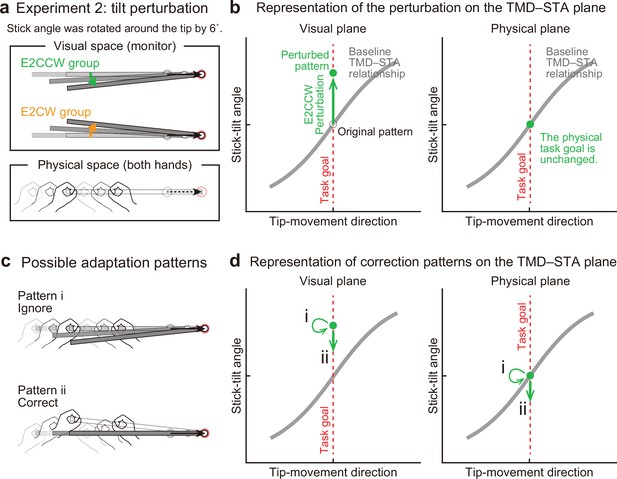
Experiment 2: End-effector irrelevant visual perturbations.
(a) During the adaptation phase of Experiment 2, the stick-tilt angle was rotated around the tip. The perturbation of ±6° was imposed from the first trial. Participants received either the counterclockwise perturbation (green, E2CCW group) or the clockwise perturbation (orange, E2CW group). (b) On the visual plane, the perturbation is expressed as a vertical shift of the state along the task goal (dashed red line). On the physical plane, the perturbation does not influence the task goal. Note that, in both planes, the states are on the task goal lines. The formats are the same as in Figure 4b. (c) Participants may not change the movement pattern because the perturbation does not affect the tip position (pattern i, top). Alternatively, the perturbation can lead to a stick-tilt correction (pattern ii, bottom). (d) These strategies are expressed as a shift on the plane. Note that pattern i means that there is no change in the movement pattern.
Figure 7 with 1 supplement
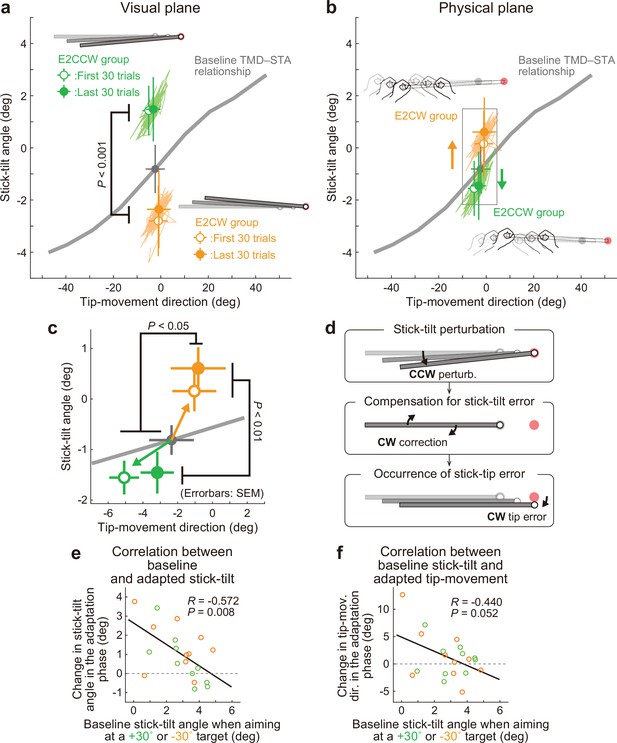
Experiment 2: Adaptation patterns to end-effector irrelevant visual perturbations.
(a) Movement patterns are shown by green (E2CCW group) and orange (E2CW group) plots on the visual plane (N=10 participants for each group). The open and filled plots represent the movement patterns in the first and last 30 trials, respectively, during the adaptation phase (mean ± SD, across participants). (b) On the physical plane, the separated movement patterns between both groups showed that participants corrected the end-effector irrelevant stick-tilt errors. (c) The enlarged plot of the squared area in b shows that end-effector relevant tip-movement directional errors accompanied the adaptation. These effects persisted until the end of the adaptation phase (two-way repeated-measures ANOVAs). (d) Schematics of how the stick-tilt perturbation altered the movement patterns. (e, f) How participants tilted the stick during the baseline phase was negatively correlated with the stick-tilt angle and the tip-movement direction. To control for the individual variability, the baseline stick-tilt angle or tip-movement direction when aiming at the 0° target was subtracted from each value.
Figure 7—figure supplement 1
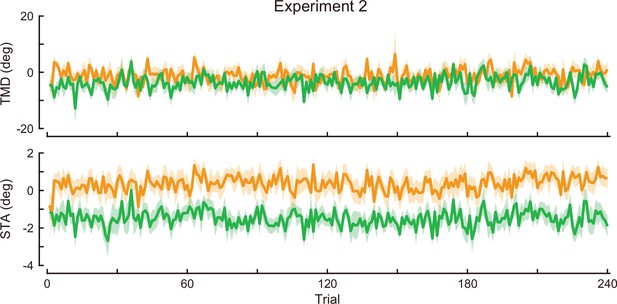
Time-course of the movement pattern in the adaptation phase.
Changes in the movement pattern in the physical space are shown (the tip-movement direction [top] and stick-tilt angle [bottom]). The data shows mean ± SEM across participants. The green and orange plots indicate E2CCW group and E2CW group, respectively (N=10 participants for each group).
Figure 8
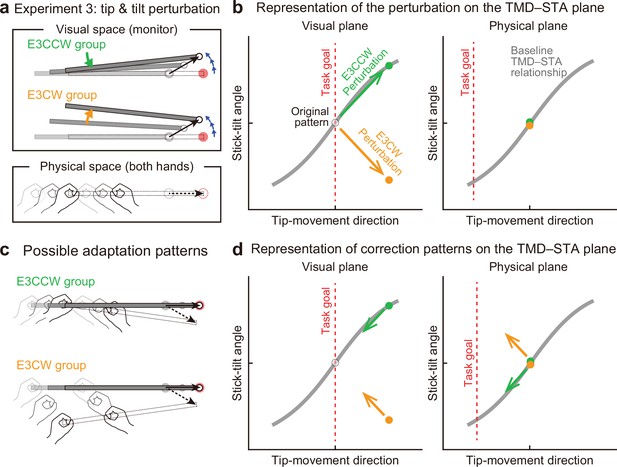
Experiment 3: Interaction between end-effector relevant and end-effector irrelevant visual perturbations.
(a) During the adaptation phase of Experiment 3, both the CCW tip perturbation and the CCW or CW stick-tilt perturbation were introduced. The participants were assigned to the CCW stick-tilt rotation condition (green, E3CCW group) or the CW stick-tilt rotation condition (orange, E3CW group). (b) These visual perturbations can be expressed as state shifts on the visual plane (green and orange arrows for E3CCW and E3CW groups, respectively). (c) The adaptation pattern to reduce visual errors (top: E3CCW group, bottom: E3CW group). (d) On the physical plane, the correction pattern required for the E3CCW group is aligned with the baseline TMD–STA relationship (green arrow), whereas the correction pattern required for the E3CW group is orthogonal to the baseline TMD–STA relationship (orange arrow).
Figure 9 with 1 supplement
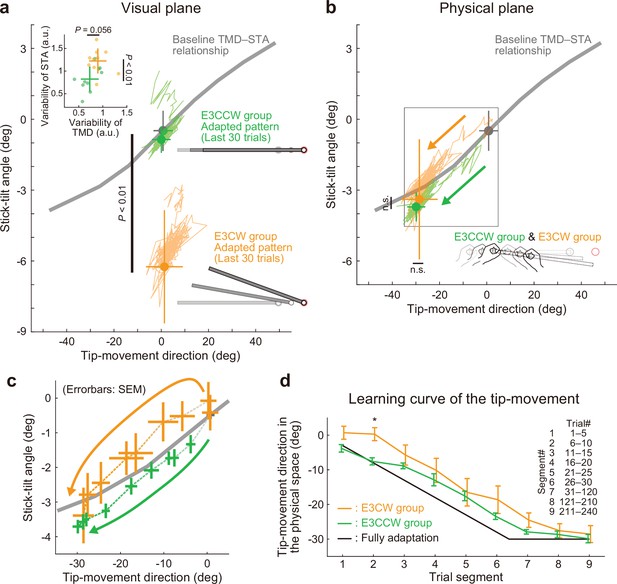
Experiment 3: Adaptation patterns to end-effector relevant and end-effector irrelevant visual perturbations.
(a) Adaptation patterns on the visual plane are shown (same formats as Figure 5a). A green (orange) plot represents the adapted movement pattern in the E3CCW group (E3CW group) (N=10 participants for each group). The tip-movement direction did not significantly differ (t-test, t(18) = –0.473, p=0.642), while the stick-tilt angle remained a significant difference between groups (t-test, t(18) = 6.920, p<0.001). A trial-by-trial variability of the movement pattern in the latter adaptation phase (trial# 121–240) showed a difference between groups (t-test, tip-movement direction: t(18) = –2.046, p=0.056, stick-tilt angle, t(18) = –3.235, p=0.005) (b) Similarly, the adapted movement patterns on the physical plane did not show a significant difference (t-test, tip-movement direction: t(18) = –0.479, p=0.638, stick-tilt angle: t(18) = –0.386, p=0.704). (c) However, the adaptive processes appeared to be different. The movement patterns of the two groups are compared using a repeated-measures MANOVA. A multivariate analysis revealed a significant effect of group (Pillai’s trace F(8, 162)=0.155, p<0.001) and trial segment (Pillai’s trace F(8, 162)=0.719, p<0.001); no significant interaction can be observed (Pillai’s trace F(8, 162)=0.039, p=0.982). The definition of trial segments is the same as that shown in Figure 5c. (d) The learning curves for the tip-movement. The adaptation in the E3CW group was always delayed but showed a significant difference only during the early phase (trial segment 2: t-test, t(18) = –3.684, Bonferroni-corrected p<0.05).
Figure 9—figure supplement 1
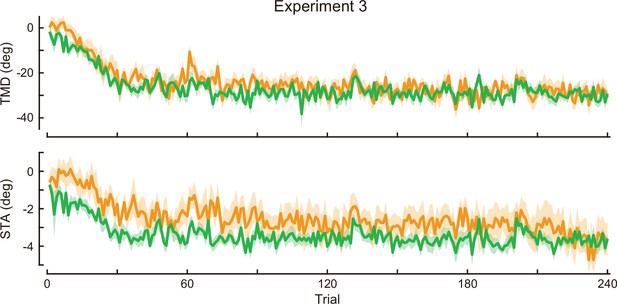
Time-course of the movement pattern in the adaptation phase.
Changes in the movement pattern in the physical space are shown (the tip-movement direction [top] and stick-tilt angle [bottom]). The data shows mean ± SEM across participants. The green and orange plots indicate E3CCW group and E3CW group, respectively (N=10 participants for each group).
Figure 10
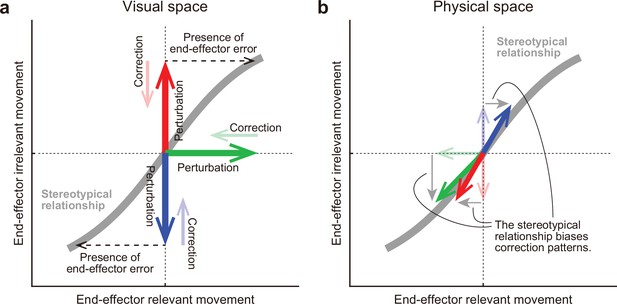
A hypothesis for how the motor system alters the movement pattern of redundant system.
The motor system develops a stereotypical relationship in redundant space, possibly through an optimization process (a gray line). (a) In the visual space, this relationship plays a crucial role for the motor system in how it should implicitly respond to the various visual perturbations (bold arrows) in the redundant space. The motor system tries to eliminate the dissociation of the perturbed state from the original state (thin arrows). According to the relationship, the motor system interprets end-effector irrelevant errors (red or blue) as evidence that end-effector relevant errors have been also produced (black dashed arrows). (b) However, the correction patterns are constrained by the relationship in the physical space. The relationship determined which movement pattern the motor system should perform. Thus, the correction patterns gravitate toward the stereotypical relationship (bold arrows).
Author response image 1
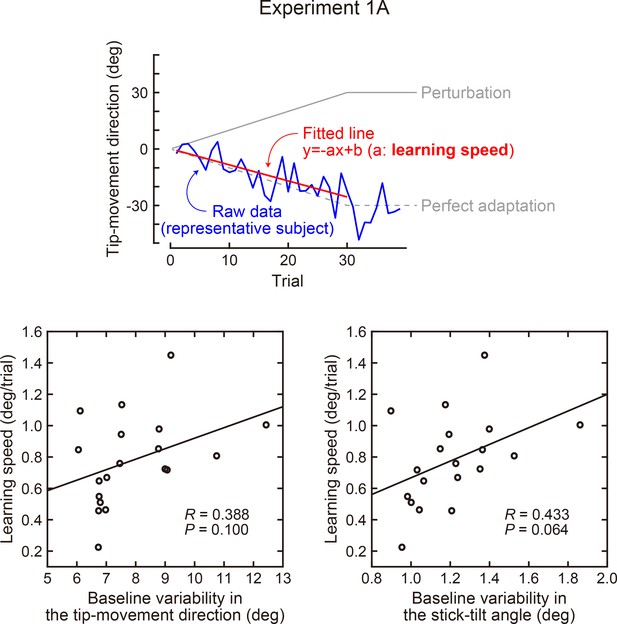
Correlation between the baseline variability and learning speed (Experiment 1A).
In Exp 1A, the rotation of the tip-movement direction was gradually increased by 1 degree per trial up to 30 degrees. The learning speed was quantified by calculating how quickly the direction of movement followed the perturbation (upper panel). The lower left panel shows the variability of the tip-movement direction versus learning speed, while the lower right panel shows the variability of the stick-tilt angle versus learning speed. Baseline variability was calculated as a standard deviation across trials (trials in which a target appeared in a 0-degree direction).
Author response image 2
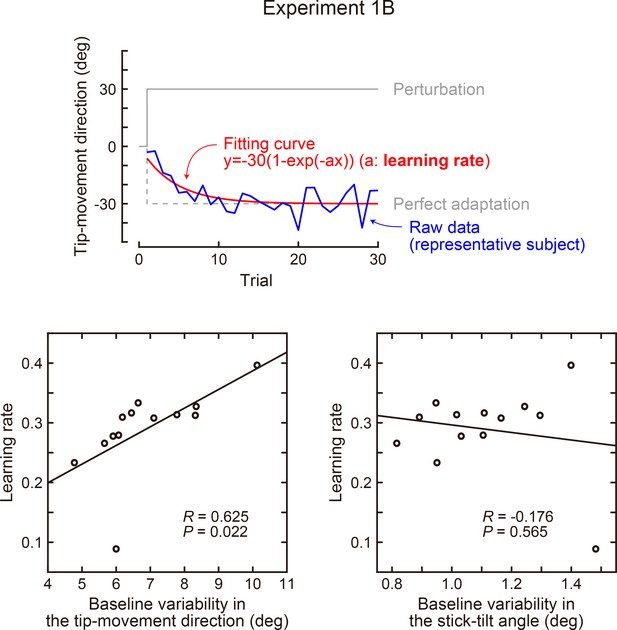
Correlation between the baseline variability and learning speed (Experiment 1B).
In Exp 1B, the rotation of the tip-movement direction was abruptly applied from the first trial (30 degrees). The learning speed was calculated as a time constant obtained by exponential curve fitting. The lower left panel shows the variability of the tip-movement direction versus learning speed, while the lower right panel shows the variability of the stick-tilt angle versus learning speed. Baseline variability was calculated as a standard deviation across trials (trials in which a target appeared in a 0-degree direction).
Author response image 3
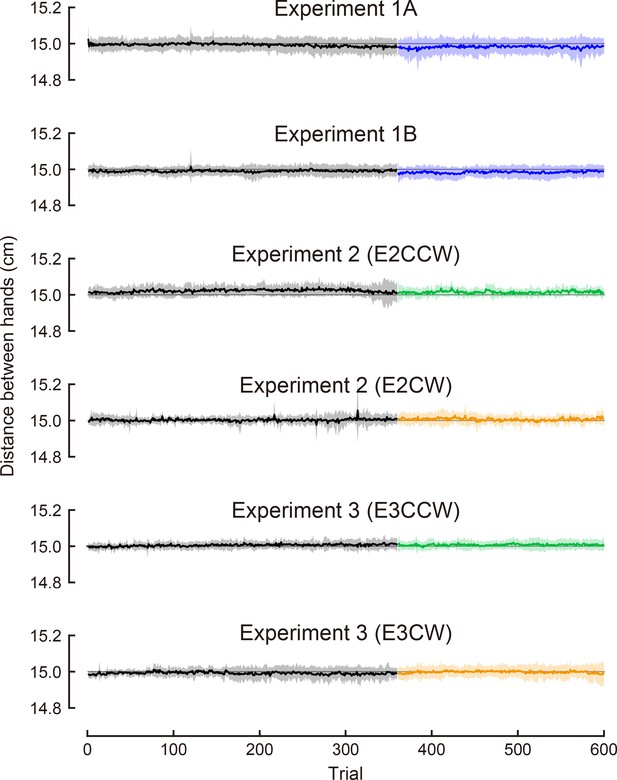
The distance between hands during the task.
We show the average distance between hands for each trial. The shaded area indicates the standard deviation across participants.
Author response image 4
Time course changes in the distance between hands during the movement.
The color means the trial epoch shown in the right legend.
Author response image 5
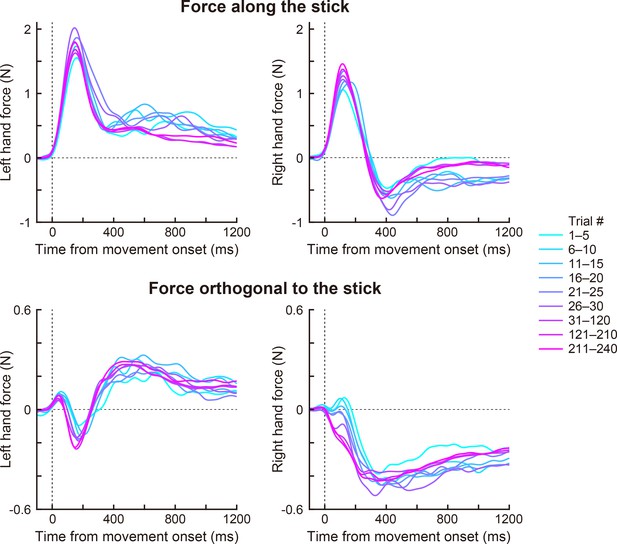
The force profile during the movement (Exp 1A).
We decomposed the force of each handle into the component along (upper panels) and orthogonal to the stick (lower panels). Changes in the force profiles in the adaptation phase are shown (left: left hand force, right: right hand force). The colors (magenta to cyan) mean trial epoch shown in the right legend.
Author response image 6
Stick-tip manipulation patterns when the length of the stick varied.
Author response image 7
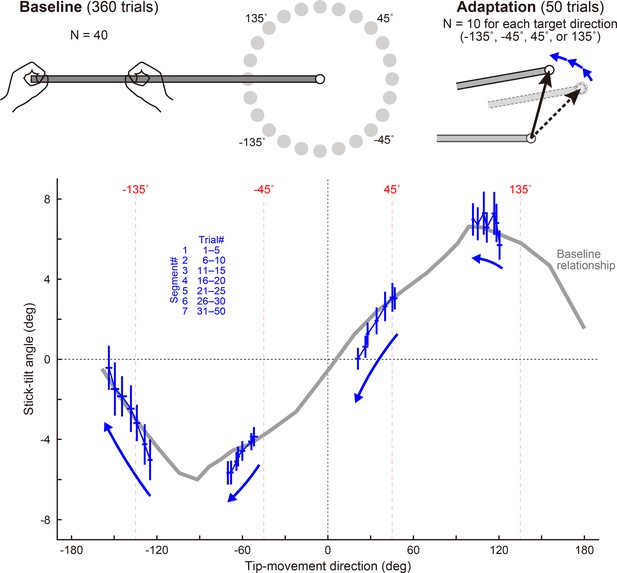
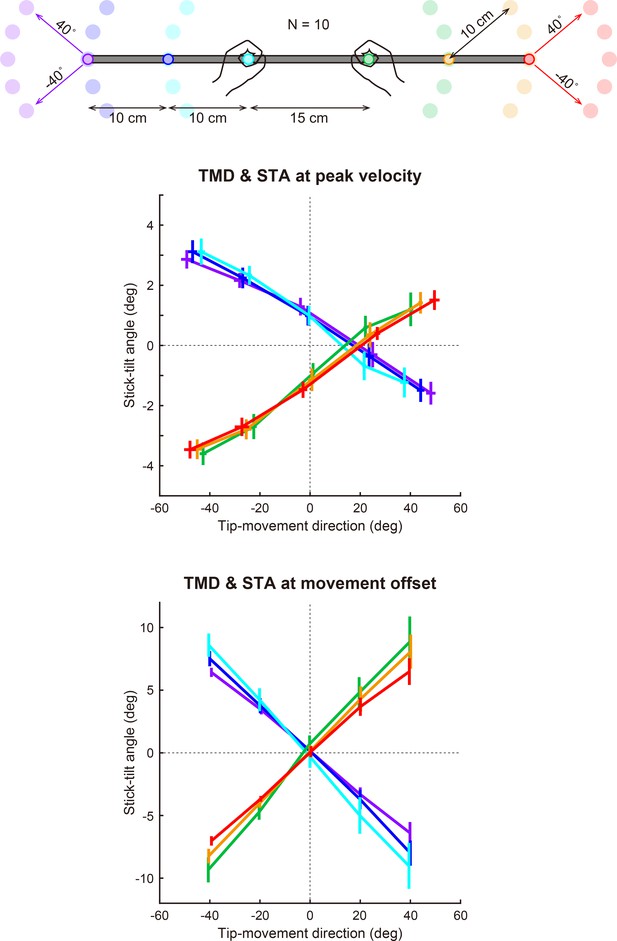
Patterns of adaptation when using the other targets.
In the baseline phase, 40 naïve participants moved a stick tip to a peripheral target (24 directions). They showed a stereotypical relationship between the tip-movement direction and the stick-tilt angle (a bold gray curve). In the adaptation phase, participants were divided into four groups, each with a different target training direction (lower left, lower right, upper right, or upper left), and visual rotation was gradually imposed on the tip-movement direction. Irrespective of the target direction, the adaptation pattern of the tipmovement and stick-tilt followed with the baseline relationship.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Implicit motor adaptation patterns in a redundant motor task manipulating a stick with both hands
eLife 13:RP96665.
https://doi.org/10.7554/eLife.96665.3
