The identification of extensive samples of motor units in human muscles reveals diverse effects of neuromodulatory inputs on the rate coding
- Department of Bioengineering, Faculty of Engineering, Imperial College London, United Kingdom
- Nantes Université, Laboratory 'Movement, Interactions, Performance', France
- Université Côte d'Azur, LAMHESS, France
- The University of Queensland, School of Biomedical Sciences, Australia
- Department of Integrative Physiology, University of Colorado Boulder, United States
Figures
Figure 1 with 2 supplements
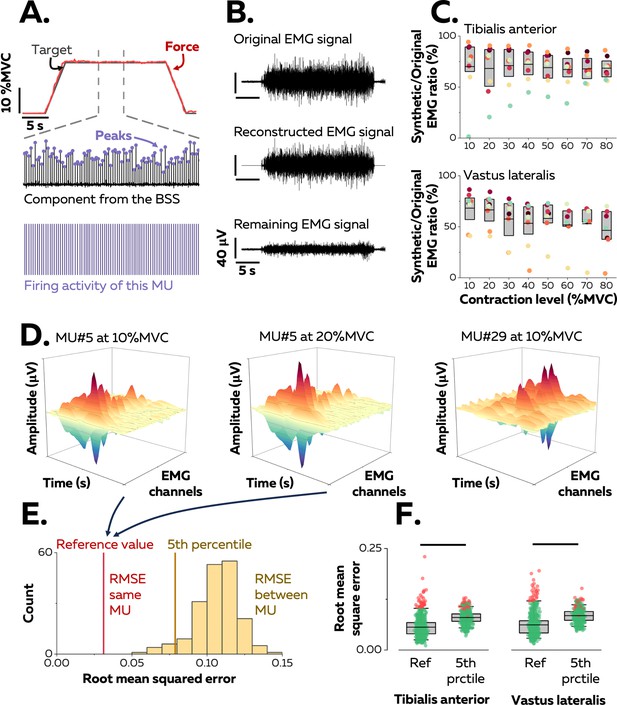
Identification of motor units in two human muscles.
(A) We used a blind-source-separation (BSS) algorithm to decompose the overlapping activity of motor units (MU) into spike trains during a force-matching trapezoidal task (red trace). (B) We reconstructed synthetic electromyographic (EMG) signals by summing the trains of action potentials from all the identified motor units and interpreting the remaining EMG signal as the part of the signal not explained by the decomposition. (C) We calculated the ratio between the powers of synthetic and original EMG signals to estimate the proportion of the signal variance explained by the decomposition. Each data point indicates the average value for one participant. (D) We estimated the uniqueness of each identified motor unit within the pool by calculating the root-mean-square error (RMSE) between the distributions of action potentials of the same motor unit across contractions (two panels on the left, reference value in E) and between motor units (left vs. right panels, distribution of RMSE between motor units in yellow in E). (F) Each motor unit was unique within the pool when the RMSE between its distributions of action potentials across target forces (reference value) was less than the 5th percentile of the distribution of RMSE with the rest of the motor units. Motor units considered as outliers in F (red data points) were removed from the analysis due to potential errors in tracking between contractions. Each data point is a motor unit, the box represents 25th–75th percentiles of the distribution of data, and the black line shows the median. The horizontal thick line denotes a statistical difference between reference values and 5th percentiles for each muscle.
Figure 1—figure supplement 1
Validation of electromyographic decomposition and motor unit tracking.
We used two approaches to validate the electromyographic decomposition. First, we simulated a pool of 150 motor units producing forces from 10% to 80% of the maximal excitation. Electromyographic signals were simulated from either 16 intramuscular electrodes (black horizontal line, top panels) or 64 surface electrodes (dark red curves on the left of top panels). Each of the grey elliptical shapes represents the cross-sectional area of the simulated muscle. We identified motor units using blind source-separation, with their territories displayed in red in the top panels. We then calculated the rate of agreement between the series of discharge times identified from the decomposition and simulated. Each data point is a motor unit, and the horizontal black line depicts the median. After this, we used the two-source validation approach, i.e., the comparison of discharge times identified from intramuscular and surface electromyographic signals. A participant performed trapezoidal isometric contractions with plateaus ranging from 10% to 80% of the maximal force while we recorded surface signals with a grid of 128 electrodes and intramuscular signals with 40 electrodes along a thin film that was inserted into the muscle with a hypodermic needle. Intramuscular and surface electromyographic signals were both decomposed and two motor units were matched between intramuscular and surface signals. We calculated the rate of agreement between the series of discharge times. It is worth noting that we identified the same number of discharge times with both methods. A rate of agreements less than 100% reflects misalignments of some discharge times with the surface signals due to the propagation of the action potentials through the tissue and potential overlapping action potentials at the surface of the skin. Finally, we validated the tracking method using the simulated signals, with high percentages highlighting the high accuracy of our approach.
Figure 1—figure supplement 2
Recruitment thresholds of motor units tracked across contractions.
We tracked motor units across contractions using their unique distribution of action potentials within the grid of 256 electrodes. Then, we estimated their recruitment thresholds as the average of force over a window of 10 ms centred around the first discharge time. The recruitment thresholds, estimated for each contraction where the motor unit was identified, are displayed for each participant. A series of data points connected with a line of the same colour is a motor unit. TA, tibialis anterior; VL, vastus lateralis; MVC, maximal voluntary contraction level; P1, participant #1.
Figure 2 with 1 supplement
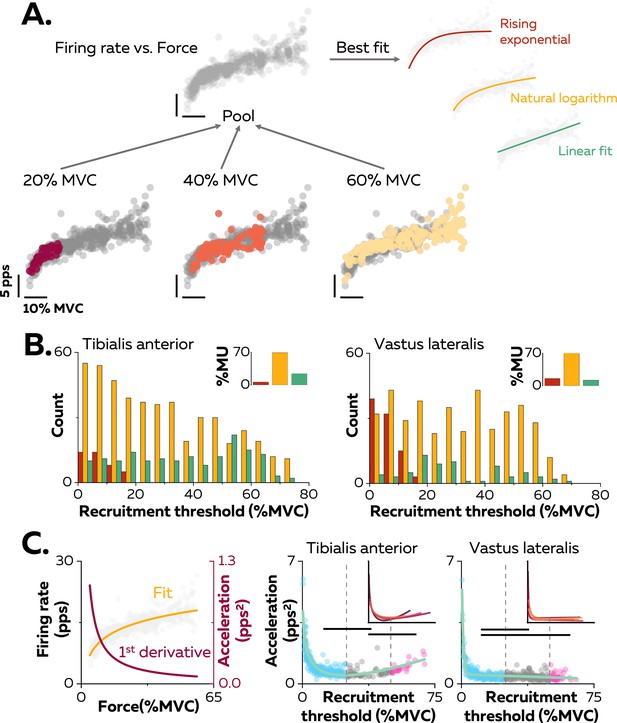
Non-linear rate coding of motor units.
(A) The relation between firing rate (pulses per second, pps) and the applied force during the ramp-up phase of the contraction was determined by concatenating the instantaneous firing rates for each motor unit (grey data points) recorded over all the contractions where it was identified, as shown here for one motor unit (coloured data points for contractions at 20%, 40%, and 60% MVC). The derived relations were then fitted with three different functions: linear (green), rising exponential (dark red), and natural logarithm (yellow), to characterise the input-output function of each motoneuron. (B) The motor units were grouped according to their best fit. The graphs show the distribution of these groups as a function of recruitment thresholds (RT) for each muscle. The inset panels depict the percentage of motor units (MU) in each group. (C) The initial acceleration of firing rate was derived from force-firing rate relation fitted with the natural logarithm (f(force)=a*ln(force)+b; yellow trace) and its first derivative (f(force)=a/force; dark red trace). The right panels show the distribution of initial acceleration values relative to recruitment threshold (RT) for all participants (n=328 motor units for tibialis anterior [TA] and n=393 motor units for vastus lateralis [VL]). Each data point indicates a motor unit. The horizontal thick lines denote a statistical difference between the motor units groups (low-threshold=blue; medium-threshold=grey; high-threshold=pink). The green line depicts the non-linear fits of these relations for the TA and the VL. Similar fits were observed for all the participants (inset panels).
Figure 2—figure supplement 1
Relations between force and firing rates fitted with a natural logarithm.
We reported the relations between instantaneous motor units firing rates and the applied force. Then, we fitted these relations for each motor unit using a natural logarithm function (left panels). The non-linearities in the relations depict the influence of neuromodulatory inputs to motoneurons on the transformation between the synaptic inputs and the motor unit firing rates. To quantify the impact of the amplification effect of these neuromodulatory inputs, we estimated the acceleration of firing rate as the first derivative of the fitted firing rate/force curves (right panels). The fits are drawn over the range of forces where the motor unit was firing during the ramp-up phases of the contractions. Each line is a motor unit. MVC, maximal voluntary contraction level.
Figure 3
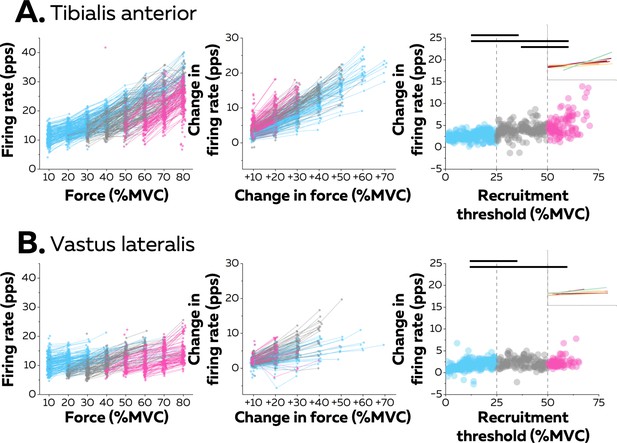
Motor unit firing rates across contraction levels.
The left column shows average firing rate (pulses per second, pps) during the force plateaus for each tracked motor unit across contraction levels for all participants from tibialis anterior (TA) (n=998 motor units; A) and vastus lateralis (VL) (n=1016 motor units; B). Each data point indicates one motor unit, and each line connects the firing rates of this motor unit across contractions. The colour scale identifies the three groups of motor units based on recruitment threshold: low (blue), medium (grey), and high (pink). The middle column depicts the change in firing rates between contractions separated by 10–70% of the maximal voluntary contraction level (MVC) of force. The right column shows the relation between the rate of increase in firing rate between successive target forces (e.g. between 10% and 20% MVC) and the recruitment threshold of the motor unit. These relations were fitted with a linear function (coloured lines in the inset panels) for each participant. The horizontal thick line denotes a statistical difference between motor units grouped by recruitment thresholds.
Figure 4
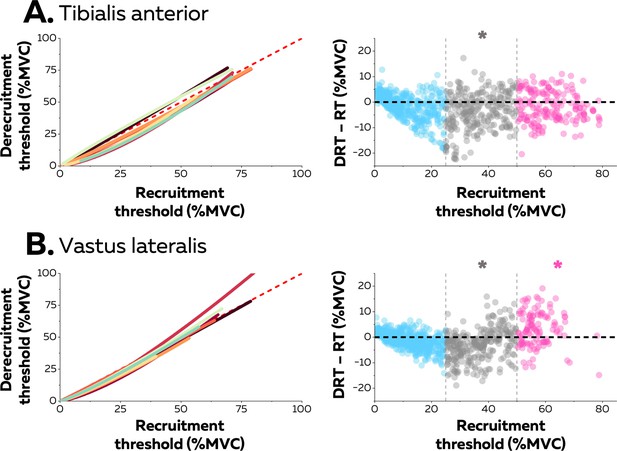
Hysteresis between recruitment and derecruitment thresholds.
The left column depicts the relations between the recruitment and derecruitment thresholds of each motor unit from tibialis anterior (TA) (A) and vastus lateralis (VL) (B). These relations were fitted for each participant (coloured lines) using either non-linear or linear regressions. The values below the dashed red line (recruitment threshold = derecruitment threshold) show a positive hysteresis between recruitment and derecruitment thresholds, the values above a negative hysteresis. The right column shows the difference between the recruitment and derecruitment thresholds, with negative values showing a positive hysteresis with recruitment threshold greater than derecruitment threshold and the positive values indicating the converse (a negative hysteresis). Each data point is a motor unit. The asterisk denotes a statistical difference between the hysteresis values for motor units grouped according to recruitment threshold (low = blue; medium = grey; high = pink) and the absence of a hysteresis (dashed horizontal line).
Author response image 1
Tables
Table 1
Mean ± standard deviation (range) for the number of motor units across the eight target forces and two muscles.
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | 80% | |
|---|---|---|---|---|---|---|---|---|
| TA | 38 ± 25 (1–73) | 45 ± 24 (21–83) | 50 ± 27 (24–95) | 49 ± 26 (24–93) | 45 ± 27 (15–93) | 40 ± 25 (14–80) | 37 ± 26 (14–84) | 34 ± 19 (9–60) |
| VL | 44 ± 17 (17–63) | 46 ± 20 (19–71) | 42 ± 20 (10–67) | 34 ± 18 (3–56) | 32 ± 15 (5–53) | 26 ± 13 (3–38) | 26 ± 14 (1–38) | 20 ± 13 (1–37) |
-
TA, tibialis anterior; VL, vastus lateralis.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The identification of extensive samples of motor units in human muscles reveals diverse effects of neuromodulatory inputs on the rate coding
eLife 13:RP97085.
https://doi.org/10.7554/eLife.97085.3
