Physiological magnetic field strengths help magnetotactic bacteria navigate in simulated sediments
- Max Planck Institute of Colloids and Interfaces, Department Theory and Biosystems, Germany
- Max Planck Institute of Colloids and Interfaces, Department Biomaterials, Germany
- Physics Department, TU München, Germany
- University of Göttingen, Institute for the Dynamics of Complex Systems, Germany
- Charité - Universitätsmedizin Berlin, Department for Operative, Preventive and Pediatric Dentistry, Germany
- Institute for Bioengineering, School of Engineering, University of Edinburgh, United Kingdom
- Aix-Marseille Université, CEA, CNRS, BIAM, France
Figures
Figure 1 with 2 supplements
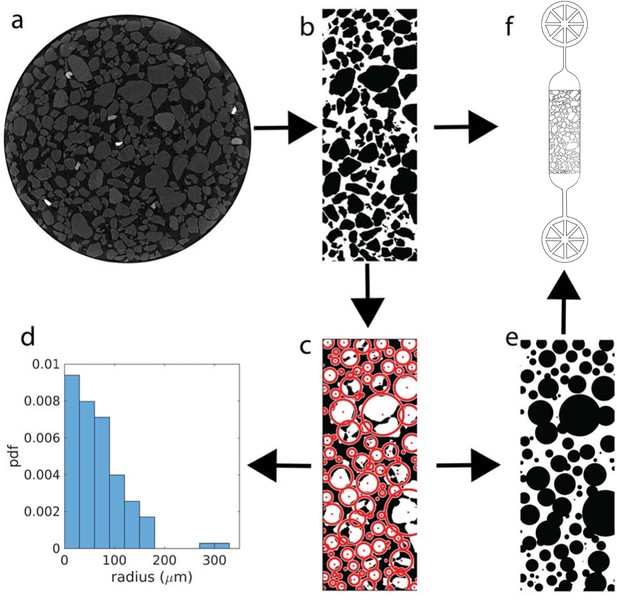
Construction of sediment-mimicking obstacle channels.
(a) Micro-computer tomography slices of sediment sampled (diameter 4mm) are cropped out to ignore border effect due to the reconstruction and binarized (b). The binarized images are then fitted with circles (c) for statistical analysis (grain size distribution in d) and for construction of arrays of pillar-shaped obstacles (e). The images of irregular grains (b) and fitted circles (e) are used as masks to design microfluidic channels with obstacle arrays (f), in which the bacteria are injected in the middle channel (3.5 mm × 1.2 mm × 10 μm) where they encounter the obstacles.
Figure 1—figure supplement 1
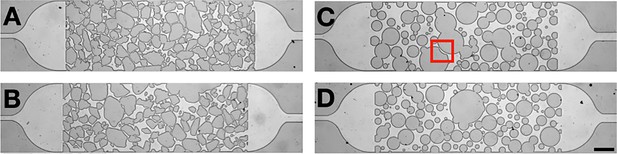
Two microfluidic channels with irregularly shaped (A, C) obstacles and the corresponding channels with rounded obstacles (B, D).
Note that in (C), a narrow channel has been cut out of the big obstacle in the center (indicated by the red square), as it would block the channel completely. The scale bar is 150 μm.
Figure 1—figure supplement 2
Masks for all obstacle arrays used in this study.
Left column: irregular shaped obstacles based on 2d μCT images of sand samples, right column: rounded obstacle.
Figure 2
Analysis of micro-computer tomography images of a sediment sample in water.
(a) Slice of the sediment sample, (b) cube from the center of the cuvette, (c) and (d) examples of water gaps rendered with the Amira software. (e) Distribution of the smallest grain dimension (i.e. trabecular thickness analyzed with CTAn) with Gaussian fit , = 3.83, = 0.5903, corresponding to a mean sand grain diameter of 46 μm. (f) Distribution of the water gap size (i.e. trabecular separation) with Gaussian fit , = 42.94 μm, = 28.66 μm. (g) Percentage of sand over water as function of the distance from the bottom of the cuvette as obtained from 2D slices of the μCT images (yellow filled line) and for the equivalent fit with circles (yellow dashed line). The red points show the mean radius of the fitted circles (± standard error of the mean) in μm (right axis).
Figure 3 with 3 supplements
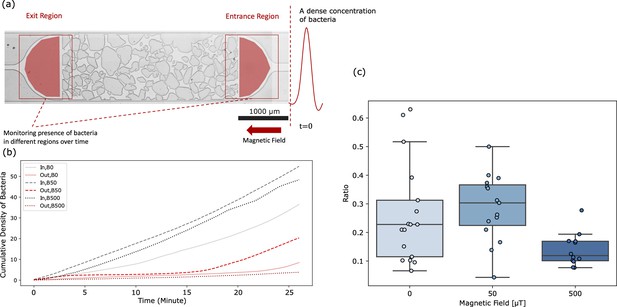
Swimming of magnetotactic bacteria through obstacle channels.
(A) View of a channel, in which the entrance (IN) and exit regions (OUT) are indicated, in which the bacterial density was monitored. Bacteria enter the IN region through an inlet that connects to a syringe containing bacteria. The magnetic field points to the left. (B) Cumulative bacterial intensity (measuring the cumulative arrival of bacteria) in these two regions, for three different field strengths. (C) Bacterial throughput, quantified by the ratio of the cumulative intensities in the OUT and IN regions as function of the magnetic field. The reduction of throughput by = 500 μT compared to = 50 μT is significant (Mann-Whitney test, ), the increase between = 0 and = 50 μT is weakly significant (), but agrees with the observation for a channel without obstacles in which the throughput increases monotonically with increasing field strength (Figure 3—figure supplement 3).
Figure 3—figure supplement 1
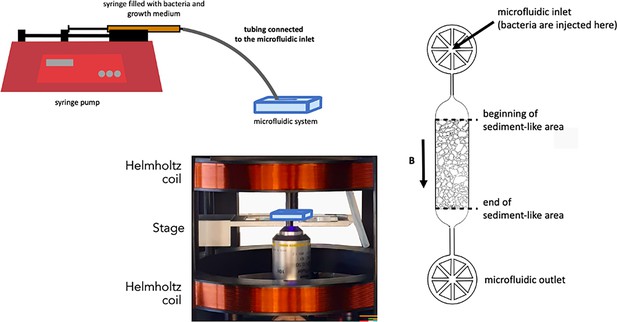
Sketch of the setup showing the microfluidic system (blue), the inlet connecting to a syringe with bacteria and growth medium, one of the three pairs of Helmholtz coils to control the magnetic field, and a detailed view of the microfluidic system.
Figure 3—figure supplement 2
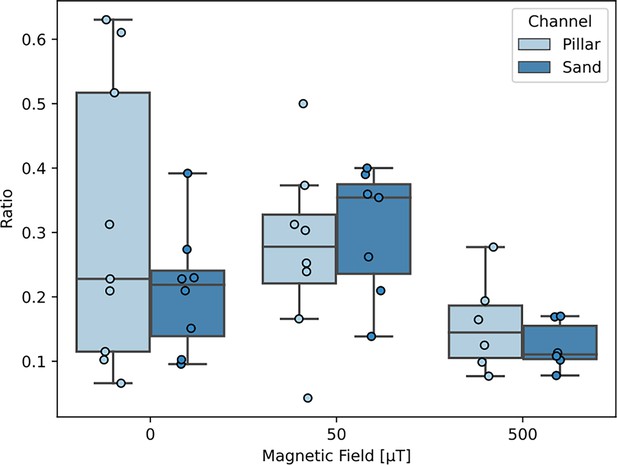
Comparison of bacterial throughput as a function of the magnetic field (0, 50, 500 μT) in channels with irregular (sand-like) obstacles and in channels with rounded (pillar-like) obstacles.
Figure 3—figure supplement 3
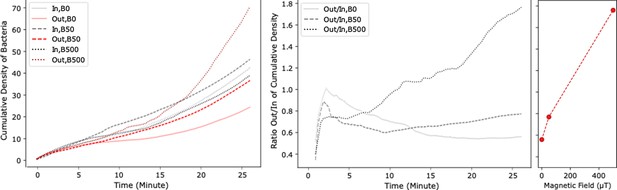
Bacterial throughput in a channel without obstacles.
(A) Cumulative density of bacteria in the IN and OUT regions of the channel. (B) Ratio of the cumulative density in the IN and OUT regions, both as functions of time and for different magnetic field strengths. (C) Dependence of the latter ratio (taken after 30 min) on the magnetic field strength. In contrast to channels with obstacles (Figure 3), a monotonic dependence is observed.
Figure 4 with 2 supplements
Sliding of bacteria on obstacle surfaces: (a) Experimental trajectories of sliding bacteria ().
(b) Trajectory of sliding particle in the simulation. The light blue region shows the spatial extent of the particle. Sliding is defined as motion in the sliding region (up to 2 μm from the surface, dotted line), provided that the particle also reaches the region where interactions with the obstacle take place (up to ≈ 0.6 μm from the surface, dashed line). The sliding distance is the distance covered tangentially to the surface. (c) Histogram of sliding distances as measured in the experiment (filled black circles) and the simulation (empty markers, for different values of the wall torque parameter α). We find good agreement for = 0.2 μm.
Figure 4—figure supplement 1
Sliding distance as a function of the pillar radius as obtained from simulations for different wall torque parameters .
The presented values show the median, error bars indicate 25th and 75th percentile. The sliding distances were extracted from obstacle channel simulation data, where pillar radii were binned into 20 μm bin sizes for statistical analysis.
Figure 4—figure supplement 2
Dependence of the sliding distance on the curvature of the pillar as obtained from the tracking bacteria in obstacle channels with cylindrical obstacles.
Figure 5
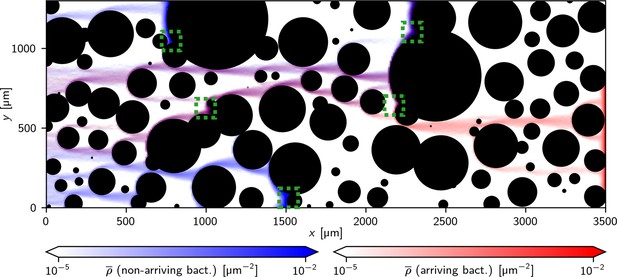
Simulated motion of bacteria in an obstacle channel: Heat maps of the time-averaged density of bacteria from simulations of 2000 bacteria for 30 min with a magnetic field , pointing from left to right.
The blue map represents bacteria that did not arrive at the right end of the simulation box during the simulated time the red heat map represents those that did. The interplay between magnetic field and the channel’s geometry creates natural paths through the channel. These paths can include traps or end in traps that are formed by overlapping obstacles (examples are indicated by the green boxes).
Figure 6
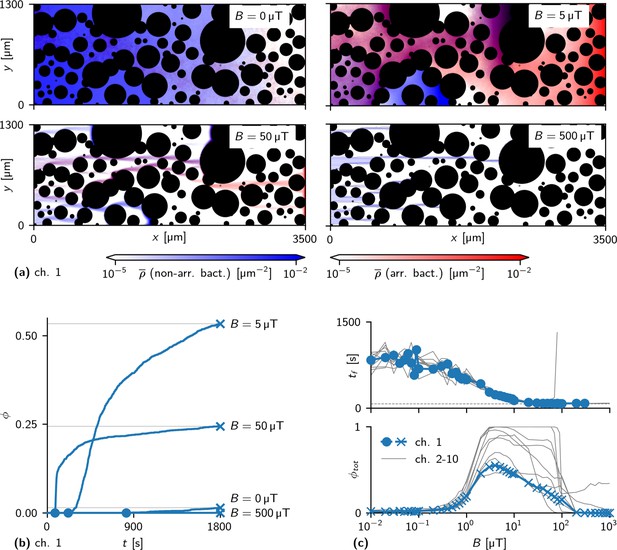
Effect of magnetic field strength on simulated swimming through obstacle channels.
(a) Motion of bacteria in a channel for different values of the field strength (heat maps of the densities of arriving and non-arriving bacteria, blue and red, respectively, as in Figure 5) (b) Fraction of simulated bacteria that have arrived up to time for different . Circles mark the first-arrival times ; crosses with thin lines mark total arrival fractions . The curve for = 500 μT remains at 0. (c) First-arrival times (top) and total arrival fraction (bottom) as a function of the field strength . With stronger fields, converges to the first-arrival time of a persistent swimmer in an empty channel (dashed gray line). shows a peak at an intermediate (optimal) field strength, which can be explained by the interplay of two opposing effects that arise with stronger fields: effectively faster motion in the direction of the field and higher susceptibility to trapping. Blue data points show the results for the channel shown in (a), gray lines show results in other channels.
Figure 7
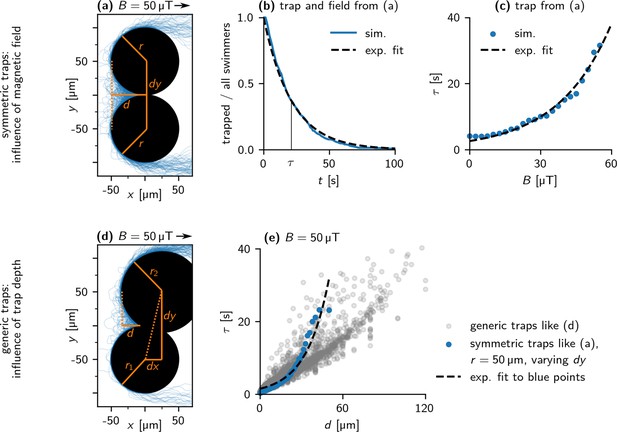
Escape from traps - Simulation.
(a) Trajectories of 100 bacteria escaping from the apex of a symmetric trap ( = 50 μT). The trap consists of two obstacles of radius 50 μm, in a distance of = 100 μm. This results in a trap depth = 50 μm. (b) Distribution of escape times of bacteria from the trap in (a). An exponential curve (dashed line) is fitted to the data, with mean escape time = 22 s. (c) Dependence of the mean escape time on the field strength for the trap in (a). An exponential curve, , is fitted to the data (dashed line). (d) Trajectories of 100 bacteria escaping from the apex of a generic trap ( = 50 μT). (e) Dependence of on for = 50 μT. Blue points show symmetric traps with both obstacles of radius 50 μm, similar to the trap in (a), gray points show a representative sample of all possible traps. An exponential curve, , is fitted to the blue data points (dashed line).
Figure 8
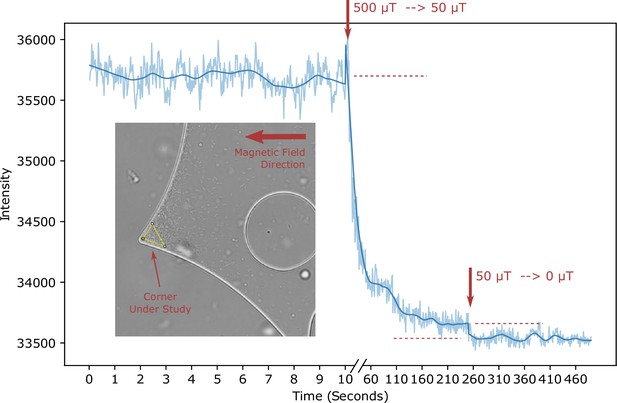
Escape from trap - Experiment.
The bacterial density in a trap (indicated by the yellow triangular area in the inset) is monitored over time. At the time points indicated by the arrows, the field strength is reduced (from 500 μT to 50 μT and from 50 μT to 0 μT, respectively), allowing the escape of trapped bacteria.
Tables
Key resources table
| Reagent type (species) or resource | Designation | Source or reference | Identifiers | Additional information |
|---|---|---|---|---|
| Strain, strain background Magnetospirillum gryphiswaldense | MSR-1 | Schleifer et al., 1991 | MSR-1 | Obtained from Schüler Lab (Univ. Bayreuth, Germany) |
| Software, algorithm | Simulation code | This paper | See Methods, section Model and simulations | |
| Other | Microfluidic channels | This paper | See Methods, section Microfluidic channel |
Table 1
Model parameters and their values.
| Parameter | Symbol | Value |
|---|---|---|
| Diameter of active particle | 1 μm (Klumpp and Faivre, 2016) | |
| Magnetic moment | 4 × 10-16 J/T (Codutti et al., 2022; Nadkarni et al., 2013) | |
| Self-propulsion speed | 50 μm/s | |
| Fluid temperature | 298 K | |
| Fluid viscosity | 8.9 × 10-4 Pa/s | |
| Magnetic field strength | [0 . . . 500] µT | |
| Surface force parameter | 4 kBT | |
| Surface torque parameter | 0.2 µm |
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Physiological magnetic field strengths help magnetotactic bacteria navigate in simulated sediments
eLife 13:RP98001.
https://doi.org/10.7554/eLife.98001.3
