The value of initiating a pursuit in temporal decision-making
- Department of Neuroscience, Johns Hopkins University School of Medicine, United States
- Kavli Neuroscience Discovery Institute, Johns Hopkins University, United States
- Microsoft, United States
- The Department of Neuroscience, Johns Hopkins University School of Medicine, United States
Figures
Figure 1
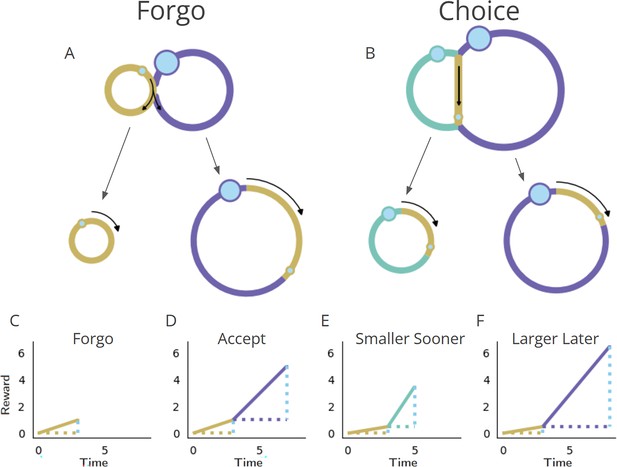
Fundamental classes of temporal decision-making regarding initiating a pursuit: ‘Forgo’ and ‘Choice’.
(A, B) (Top row) Topologies. The temporal structure of worlds exemplifying Forgo (A) and Choice (B) decisions mapped as their topologies. Forgo: A Forgo decision to accept or reject the purple pursuit. When exiting the gold pursuit having obtained its reward (small blue circle), an agent is faced with (1) a path to re-enter gold, or (2) a path to enter the purple pursuit, which, on its completion, re-enters gold. Choice: A Choice decision between an aqua pursuit, offering a small reward after a short amount of time, or a purple pursuit offering a larger amount of reward after a longer time. When exiting the gold pursuit, an agent is faced with a path to enter (1) the aqua or (2) the purple pursuit, both of which lead back to the gold pursuit upon their completion. (Middle row) Policies. Decision-making policies chart a course through the pursuit-to-pursuit structure of a world. Policies differ in the reward obtained and in the time required to complete a traversal of that world under that policy. Policies of investing less (left) or more (right) time to traverse the world are illustrated for the considered Forgo and Choice worlds. Forgo: A policy of rejecting the purple pursuit to re-enter the gold pursuit (left) acquires less reward though it requires less time to make a traversal of the world than a policy of accepting the purple option (right). Choice: A policy of choosing the aqua pursuit (left) results in less reward though it requires less time to traverse the world than a policy of choosing the purple pursuit (right). (C-F) Time/reward investment. The times (stippled horizontal lines, colored by pursuit) and rewards (stippled vertical blue lines) of pursuits, and their associated reward rates (solid lines) acquired under a policy of forgo (C) or accept (D) in the Forgo world, or, of choosing the smaller-sooner (E) or later-larger pursuit (F) in the Choice world.
Figure 2
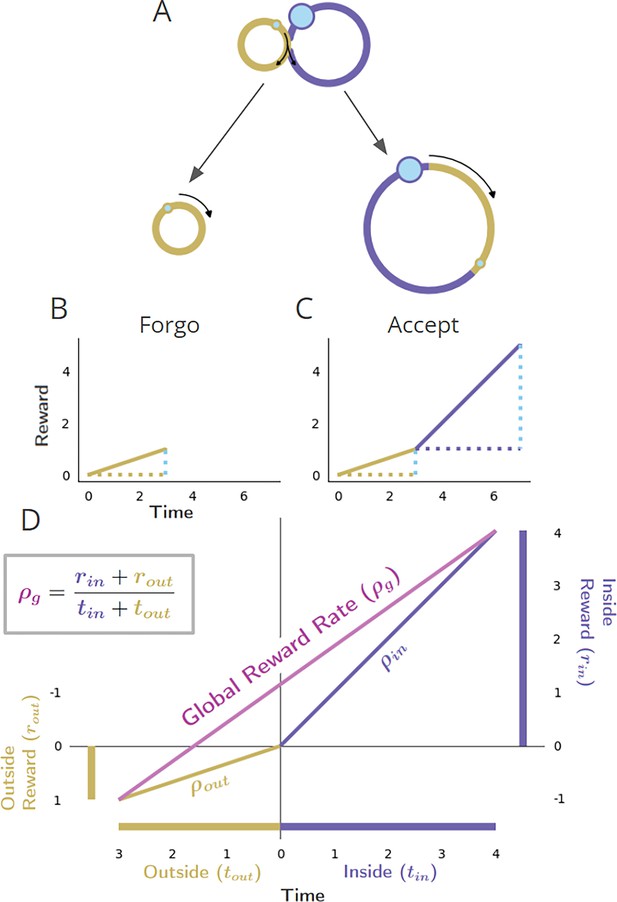
Global reward rate with respect to parceling the world into ‘in’ and ‘outside’ the considered pursuit.
(A-C) as in Figure 1 ‘Forgo’. Conventions as in Figure 1. (D) The world divided into ‘Inside’ and ‘Outside’ the purple pursuit type, as the agent decides whether to forgo or accept. The axes are centered on the position of the agent, just before the purple pursuit, where the upper right quadrant shows the inside (purple) pursuit’s average reward, time, and reward rate (ρin), while the bottom left quadrant shows the outside pursuit (gold) average reward, time, and reward rate (ρout). The global reward rate (ρg) is shown in magenta, calculated from the boxed equation. The agent may determine the higher reward rate yielding policy by comparing the outside reward rate (ρout) with the resulting global reward rate (ρg) under a policy of accepting the considered pursuit.
Figure 3 with 2 supplements
Forgo decision-making.
(A) When the reward rate of the considered pursuit (slope of the purple line) exceeds that of its outside rate (slope of gold), the global reward rate (slope of magenta) will be greater than the outside, and therefore the agent should accept the considered pursuit. (B) When the reward rates inside and outside the considered pursuit are equivalent, the global reward rate will be the same when accepting or forgoing: the policies are equivalent. (C) When the reward rate of the considered pursuit is less than its outside rate, the resulting global reward rate if accepting the considered pursuit will be less than its outside reward rate and therefore should be forgone.
Figure 3—figure supplement 1
Forgo world with n-pursuits occurring at the same frequency.
An agent experiencing a Forgo decision making world (topology as in (A), left) where n-pursuits of varying times and rewards (purple, aqua, orange) occurring at the same frequency from the default pursuit (gold) are encountered, will forgo considered pursuits that evaluate to negative subjective values using, iteratively, the policy evaluation identified in Equivalent immediate subjective value need not be calculated from option-specific estimations of global reward rate, ultimately producing the global reward-rate-optimal policy. (A) Left. Topology of pursuit world. Bottom. Sample of the experienced world under a policy of accepting all offered pursuits. Right. The purple pursuit type, plotted with respect to it being the considered pursuit engaged ‘in’, with gold, orange, and cyan pursuits occurring ‘outside’ of purple, yields a global reward rate (dashed magenta line) that has a negative y-intercept, that is a negative subjective value. Pursuits with a negative subjective value will have reward rates that are less than their ‘outside’ reward rate (slope of thin black line). Thus, when the inside reward rate is less than the outside reward rate, a reward rate-optimal agent will forgo the considered pursuit, realizing a topology as in (B). (B) This agent, when encountering the aqua pursuit will subsequently forgo the aqua pursuit as well, excluding it from its policy as it would result in negative subjective value. (C) Ultimately, the agent’s policy converges to one of accepting only the orange pursuit, as a policy of its acceptance results in a positive subjective value. x-axis projections of these line segments represent the average time spent in one or another pursuit, whereas y-axis projections of these line segments represent the average reward acquired from one or another pursuit. Pursuit: reward, time. Purple: 3, 8; Aqua: 3, 4.7; Orange 3, 2; each occurring from the default pursuit at a frequency of 0.2 per unit time in the default pursuit.
Figure 3—figure supplement 2
Forgo world with n-pursuits occurring at different frequencies.
An agent experiencing a Forgo decision making world (topology as in (A), left) where n-pursuits of varying times and rewards (purple, aqua, orange) occurring at different frequency from the default pursuit (gold) are encountered, will Forgo considered pursuits that evaluate to negative subjective values using, iteratively, the policy evaluation identified in Equivalent immediate subjective value need not be calculated from option-specific estimations of global reward rate, ultimately producing the global reward-rate-optimal policy. (A) Left. Topology of pursuit world. Bottom. Sample of the experienced world under a policy of accepting all offered pursuits. Right. The purple pursuit type, plotted with respect to it being the pursuit considered to engaged ‘in’, with gold, orange, and cyan, occurring ‘outside’ of purple, yields a global reward rate (dashed magenta line) that has a negative y-intercept, that is a negative subjective value. Pursuits with a negative subjective value will have reward rates that are less than their ‘outside’ reward rate (slope of thin black line). Thus, when the inside reward rate is less than the outside reward rate, a reward rate-optimal agent will forgo the considered pursuit realizing a topology as in (B). (B) This agent, when encountering the aqua pursuit will subsequently forgo the aqua pursuit as well, excluding it from its policy as it would result in negative subjective value. (C) Ultimately, the agent’s policy converges to one of accepting only the orange pursuit, as a policy of its acceptance results in a positive subjective value. x-axis projections of these line segments represent the average time spent in one or another pursuit, whereas y-axis projections of these line segments represent the average reward acquired from one or another pursuit. Pursuit: reward, time = Purple: 3, 8; Aqua: 3, 4.7; Orange 3, 2; occurring from the default pursuit at frequencies of 0.1, 0.2, and 0.3, respectively, per unit time in the default pursuit.
Figure 4
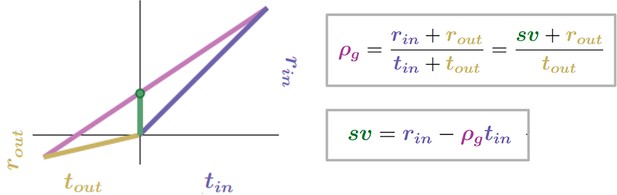
The subjective value (sv) of a pursuit is the global reward-rate-equivalent immediate reward magnitude.
The subjective value (green bar) of a pursuit is that amount of reward requiring no investment of time that the agent would take as equivalent to a policy of accepting and acquiring the considered pursuit. For this amount to be equivalent, the immediate reward magnitude must result in the same global reward rate as that of accepting the pursuit. The global reward rate obtained under a policy of accepting the considered pursuit type is the slope of the line connecting the average times and rewards obtained in and outside the considered pursuit type. Therefore, the global reward rate-equivalent immediate reward (i.e. the subjective value of the pursuit) can be depicted graphically as the y-axis intercept (green dot) of the line representing the global reward rate achieved under a policy of accepting the considered pursuit. rin = 4, tin = 4, rout = 0.7, tout = 3.
Figure 5
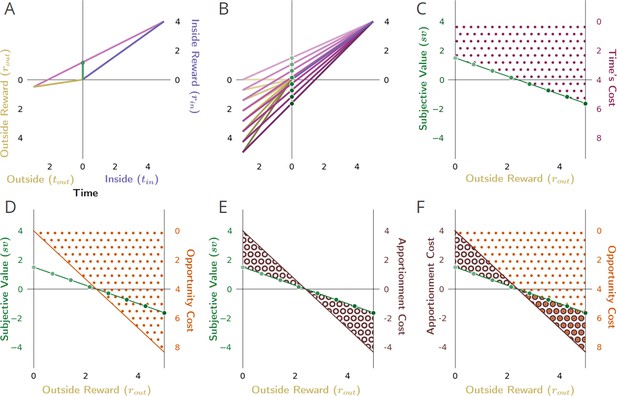
Equivalent expressions for subjective value reveal time’s cost comprises an apportionment as well as opportunity cost.
(A) The subjective value of a pursuit can be expressed in terms of the global reward rate obtained under a policy of accepting the pursuit. rin = 4, tin = 4, rout = .7, tout = 3. (B) The cost of time of a pursuit is the amount of reward earned on average in an environment over the time needed for its obtainment under a policy of accepting the pursuit. The reward rate earned on average is the global reward rate (slope of magenta line). Projecting that global reward over the time of the considered pursuit (dashed magenta line) provides the cost of time for the pursuit (vertical maroon bar). Therefore, the subjective value of a pursuit is equivalent to its reward magnitude less the cost of time of the pursuit (box equation above B). (C) Expressing subjective value with respect to the outside reward and time rather than the global reward rate reveals that a portion of a pursuit’s time cost arises from an opportunity cost (orange bar). The opportunity cost of a pursuit is the amount of reward earned over the considered pursuit’s time on average under a policy of not taking the considered pursuit (i.e. the outside reward rate, slope of gold line). Projecting the slope of the gold line over the time of the considered pursuit (dashed gold line) provides the opportunity cost of the pursuit (vertical orange bar). (D) The opportunity cost-subtracted reward (cyan bar). The triangle with sides cyan, magenta, and gold (solid and dashed) is congruent with the triangle with sides green, magenta, and gold (solid). Therefore, (E) sv is to the opportunity cost-subtracted reward, as is to . The opportunity cost-subtracted reward can thus be scaled by to yield the subjective value of the pursuit. This scaling term, which we coin ‘apportionment scaling’, is the proportion that the outside time is to the total time to traverse the world. The slope of the dashed magenta and cyan line is the global reward rate after accounting for the opportunity cost. (F) The global reward rate after accounting for the opportunity cost (dashed magenta and gold), projected from the origin over the time of the pursuit is the apportionment cost of time (brown vertical line). It is the amount of the opportunity cost-subtracted reward that would occur on average over the pursuit’s time under a policy of accepting the pursuit. (G) Time’s cost is apportionment cost plus the opportunity cost. Whether expressed in terms of the global reward rate achieved under a policy of accepting the considered pursuit (A-B) or from the perspective of the outside time and reward (C-G), the subjective value expressions are equivalent.
Figure 6
The impact of outside reward on the subjective value of a pursuit.
(A) The subjective value (green dot) of a considered pursuit type (purple) in the context of its ‘outside’ (gold) is the resulting global reward rate vector’s (magenta) intersection of the y-axis in the present (t=0). (B) A family of vectors showing that increasing the outside reward while holding the outside time constant increases the outside reward rate (slope of gold lines), resulting in increasing the global reward rate (slope of the purple lines), and decreasing the subjective value (green dots) of the pursuit. As the reward rate of the environment outside the considered pursuit type increases from lower than to higher than that of the considered pursuit, the subjective value of the pursuit decreases, becomes zero when the in/outside rates are equivalent, and goes negative when ρout exceeds ρin. (C) Plotting the subjective value of the pursuit (green dots in B) as a function of increasing the outside reward (green dotted line in C through F) reveals that the subjective value of the pursuit decreases linearly. This linear decrease is due to the linear increase in the cost of time of the pursuit (maroon dotted region) as outside reward, and thus global reward rate, increases. Subtracting time’s cost from the pursuit’s reward yields the pursuit’s subjective value as outside reward increases (green-dotted line, C through F).
Time’s cost (the area, as in C, between the pursuit’s reward magnitude and its subjective value) is the sum of (D) the opportunity cost of time (orange dotted region), and (E) the apportionment cost of time (brown annuli region), as shown in (F). (D) As the outside reward increases, the opportunity cost of time increases linearly. (E) As the outside reward increases, the apportionment cost of time decreases linearly, becomes zero when the inside and outside reward rates are equal, and then becomes negative (becomes an apportionment gain). (F) When the outside reward rate is zero, time’s cost is composed entirely of an apportionment cost. As the outside reward increases, opportunity cost increases linearly as apportionment cost decreases linearly, summing to time’s cost. This continues until the reward rates in and outside the pursuit become equivalent, at which point the subjective value of the pursuit is zero. When subjective value is zero, the cost of time is entirely composed of opportunity cost. As the outside rate exceeds the inside rate, opportunity cost continues to increase while the apportionment cost becomes increasingly negative (which is to say, the apportionment cost of time becomes an apportionment gain of time). Adding the positive opportunity cost and the now negative apportionment cost (the region of overlap between brown annuli and orange dots) continues to sum to yield time’s cost.
Figure 7
The impact of the apportionment cost of time on the subjective value of a pursuit.
(A) The apportionment cost of time can best be illustrated dissociated from the contribution of the opportunity cost of time by considering the special instance in which the outside has no net reward, and therefore has a reward rate of zero. (B) In such instances, the considered pursuit type (purple vector) still has a cost of time, however, which is entirely composed of apportionment cost. Time’s apportionment cost will decrease as the time in the outside (the family of outside time golden vectors) increases, decreasing the slope of corresponding global reward rate vectors (family of magenta vectors) and, thus, increasing the subjective value (green dots) of the considered pursuit. (C) Here, the cost of time is entirely composed of apportionment cost, which arises from the fact that the considered pursuit is contributing its proportion to the global reward rate. How much the pursuit’s time cost is (maroon dots) is thus determined by the ratio of the time spent in the pursuit versus outside the pursuit; the more time is spent outside the pursuit, the less the apportionment cost of time of the pursuit, and therefore, the greater the subjective value of the pursuit (green dotted line). (D) When apportionment cost (brown annuli) solely composes the cost of time, the cost of time decreases hyperbolically as the outside time increases, resulting in the subjective value of a pursuit increasing hyperbolically (green dotted line). Conventions as in Figure 6.
Figure 8
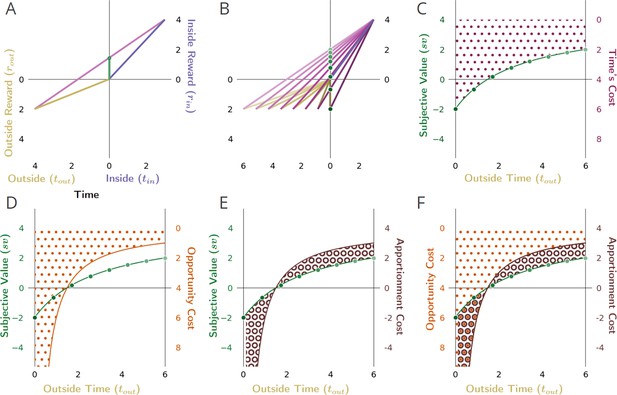
The effect of changing the outside time and thus the outside reward rate, on the subjective value of a pursuit.
(A) The subjective value (green dot) of the considered pursuit, when (B) changing the outside time, and thus, outside reward rate (green dots). (C) As outside time increases under these conditions (holding outside reward constant), the subjective value of the pursuit increases hyperbolically (green dotted line), from the negative of the outside reward magnitude to, in the limit, the inside reward magnitude. Conversely, time’s cost (right hand axis, maroon dots) decreases hyperbolically. (D) Opportunity cost (orange stippling, right hand y-axis) decreases hyperbolically as outside time increases. (E) Apportionment cost (right hand y-axis) is the difference of two hyperbolas (brown annuli area). It is initially negative, meaning that apportionment cost is a gain, as the outside reward rate is greater than the inside reward rate. This apportionment gain decreases to zero as outside time increases to make the outside and inside rates equal, and then becomes an apportionment cost (positive). (F) Summing opportunity cost and apportionment cost yields time’s cost; subtracting time’s cost from the pursuit’s reward magnitude yields the subjective value (green dotted curve). Conventions as in Figure 6.
Figure 9
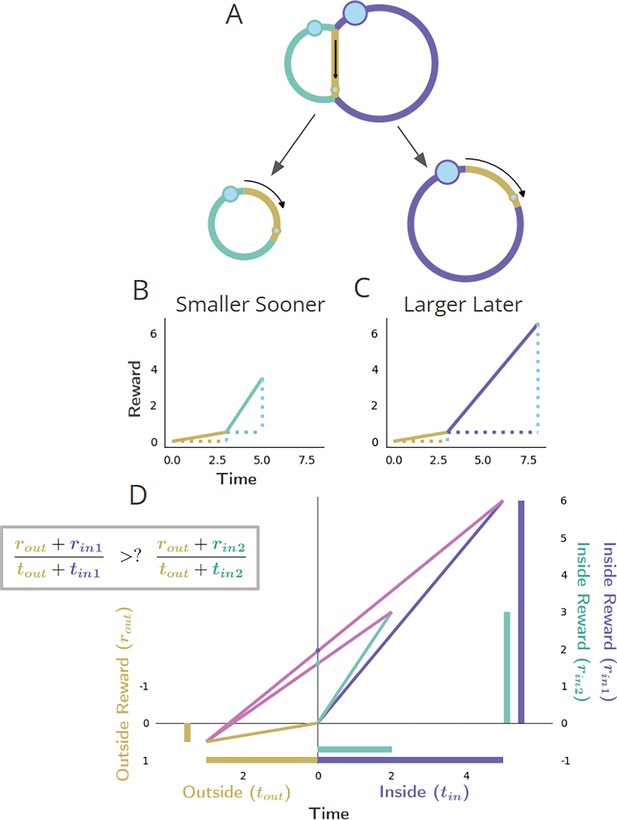
Policy options considered during the initiation of pursuits in worlds with a ‘Choice’ topology.
(A-C) Choice topology, and policies of choosing the smaller-sooner or larger-later pursuit, as in Figure 1 ‘Choice’. (D) The world divided into ‘Inside’ and ‘Outside’ the selected pursuit type, as the agent decides whether to accept the SS (aqua) or the LL (purple) pursuit. The global reward rate (ρg) under a policy of choosing SS or LL (slopes of the magenta lines) is calculated from the equation in the box to the right.
Figure 10
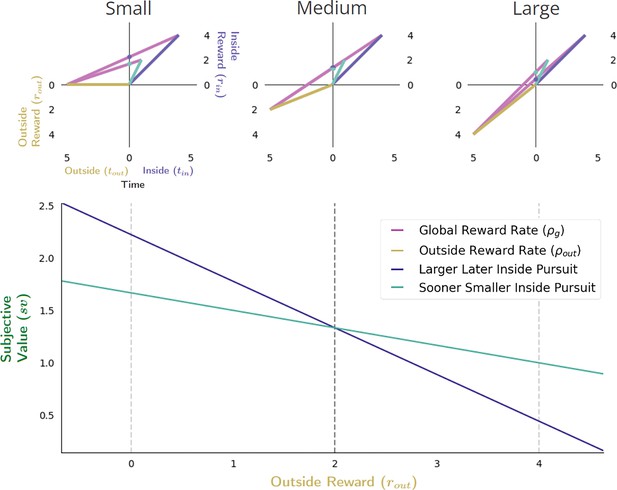
The effect of increasing outside reward on subjective value in choice decision-making.
The effect of increasing the outside reward while holding the outside time constant is to linearly increase the cost of time, thus decreasing the subjective value of pursuits considered in choice decision-making. When the outside reward is sufficiently small (top left), the subjective value of the LL pursuit can exceed the SS pursuit, indicating that selection of the LL pursuit would maximize the global reward rate. As outside reward increases, however, the subjective value of pursuits will decrease linearly as the opportunity cost of time increases. Since a policy of choosing the LL pursuit will have the greater opportunity cost, the slope of its function relating subjective value to outside reward will be greater than that of a policy of choosing the SS pursuit (bottom). Thus, outside reward can be increased sufficiently such that the subjective value of the LL and SS pursuits will become equal (top middle), past which the agent will switch to choosing the SS pursuit (top right). Vertical dashed lines (bottom) correspond to instances along top.
Figure 11
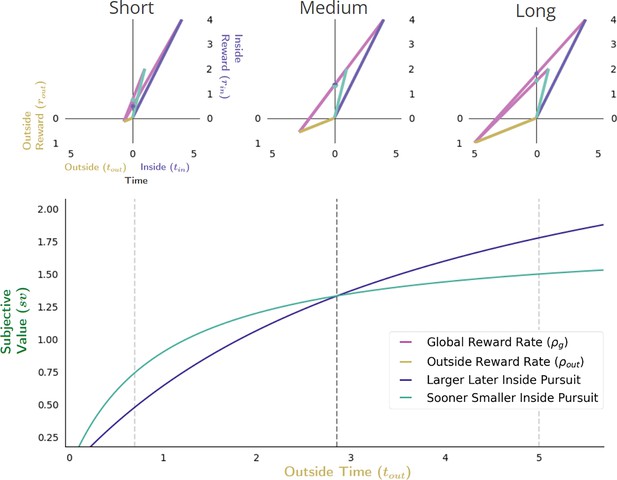
Effect of apportionment cost on subjective value in Choice decision-making.
The effect of apportionment cost can be isolated from the effect of opportunity cost by increasing the outside time while holding outside rate constant. Doing so results in decreasing the apportionment cost of the considered pursuit, thus increasing its subjective value (bottom). When the outside time is sufficiently small (top left), the apportionment cost for LL and SS pursuits will be relatively large, but can be greater still for the LL pursuit given its proportionally longer duration to the outside time and greater reward magnitude. As outside reward time increases, however, the subjective value of pursuits increase as the apportionment cost of time of the considered pursuit decreases. As apportionment costs diminish and the magnitudes of pursuits’ rewards become more fully realized, the subjective value of the LL and SS pursuits will become equal (top middle), with the LL pursuit eventually exceeding that of the SS pursuit at sufficiently long outside times (top right). Vertical dashed lines (bottom) correspond to instances along top.
Figure 12
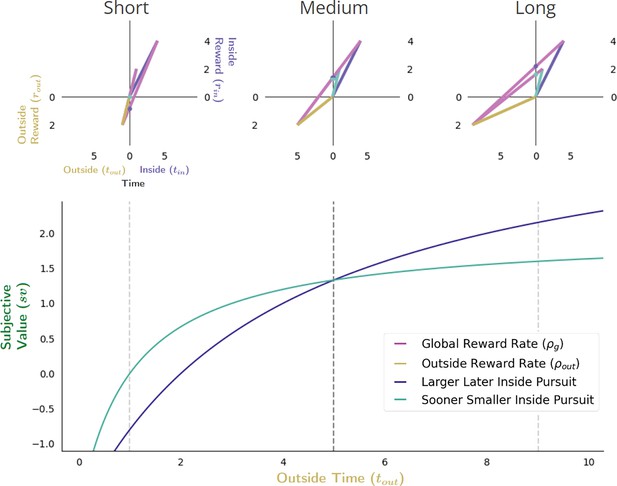
Effect of varying outside time and outside reward rate.
The effect of increasing the outside time while maintaining outside reward is to decrease the apportionment as well as the opportunity cost of time, thus increasing pursuit’s subjective value. Increasing outside time, which in turn, also decreases outside reward rate, results in the agent appearing as if to become more patient, being willing to switch from a policy of selecting the SS pursuit (upper left) to a policy of treating them equally (upper middle) at some critical threshold (vertical dashed black line, bottom), to a policy of selecting the LL pursuit (upper right). Vertical dashed lines (bottom) correspond to instances along top.
Figure 13
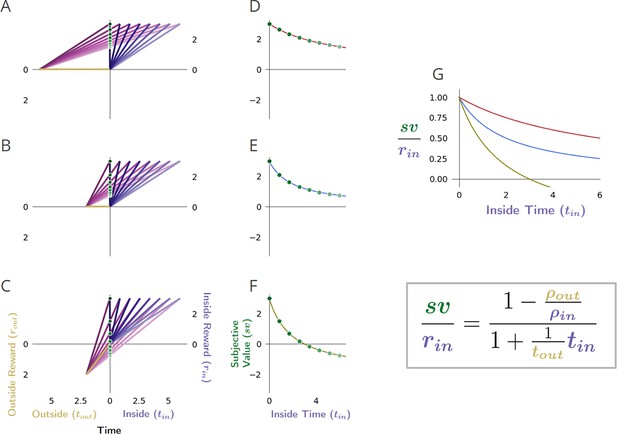
The temporal discounting function of a global reward-rate-optimal agent is a hyperbolic function relating the apportionment and opportunity cost of time.
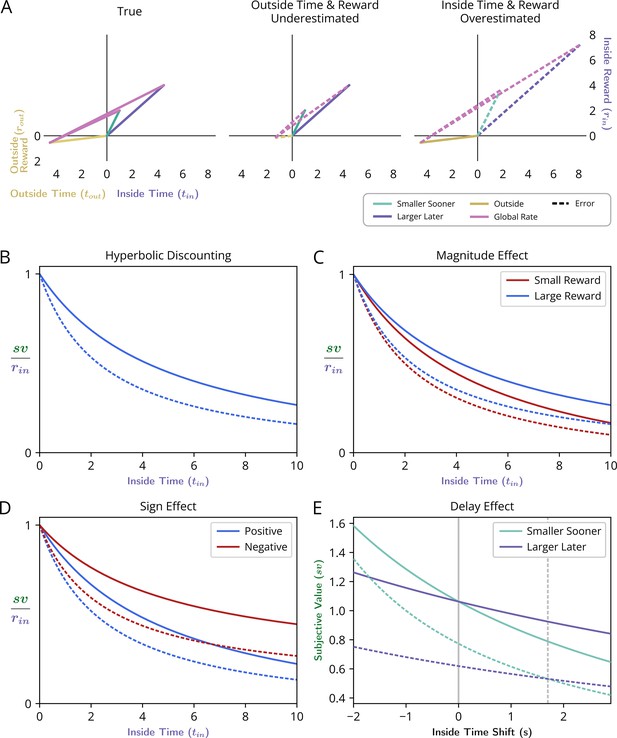
(A-C) The effect, as exemplified in three different worlds, of varying the outside time and reward on the subjective value of a pursuit as its reward is displaced into the future. The subjective value, sv, of this pursuit as its temporal displacement into the future increases is indicated as the green dots along the y-intercept in these three different contexts: a world in which there is (A) zero outside reward rate and large outside time, (B) zero outside reward rate and small outside time, and (C) positive outside reward rate and the small outside time as in (B). (D-F) Replotting these subjective values at their corresponding temporal displacement yields the subjective value-time function of the offered reward in each of these contexts. (G) Normalizing these subjective value functions by the reward magnitude and superimposing the resulting temporal discounting functions reveals how the steepness and curvature of the apparent discounting function of a reward-rate-maximizing agent changes with respect to the average reward and time spent outside the considered pursuit. When the time spent outside is increased (compare B to A)—thus decreasing the apportionment and opportunity cost of time—the temporal discounting function becomes less curved, making the agent appear as if more patient. When the outside reward is increased (compare B to C)—thus increasing the opportunity and apportionment cost of time—the temporal discounting function becomes steeper, making the agent appear as if less patient.
Figure 14
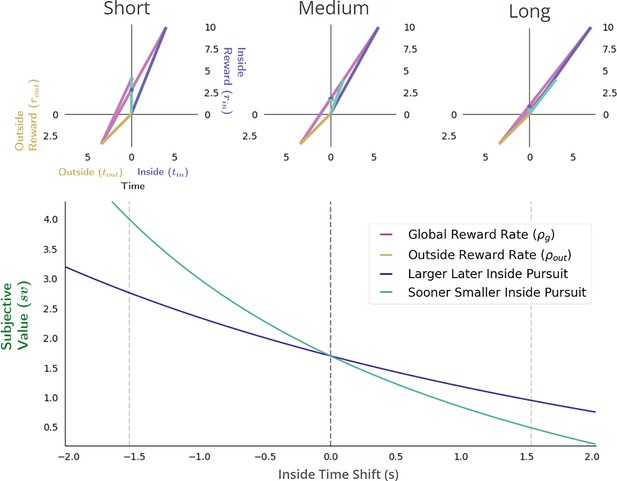
Reward-rate-maximizing agents would exhibit the ‘Delay Effect’.
A ‘switch’ in preference from a SS―when the delay to the pursuits is relatively short (upper left)―to a LL pursuit, when the delay to the pursuits is relatively long (upper right), would occur as a consequence of global reward-rate maximization. Bottom: The subjective value-time functions varying the delay to the SS (cyan) and LL (purple) pursuit with respect to the delay in which selecting either pursuit results in the same global reward-rate. Vertical dashed lines (Bottom) correspond to instances along top.
Figure 15
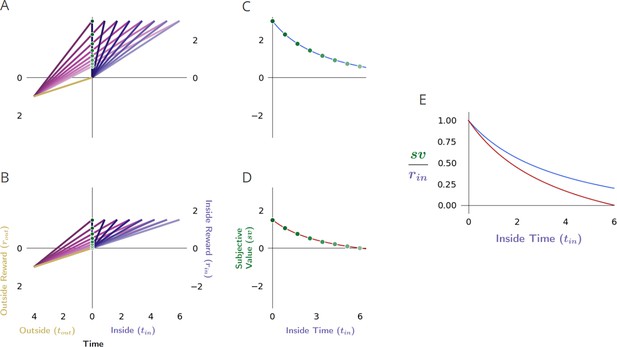
Reward-rate-maximizing agents would exhibit the ‘Magnitude effect’.
(A, B) The global reward rate (the slope of magenta vectors) that would be obtained when acquiring a considered pursuit’s reward of a given size (either relatively large as in A or small as in B) but at varying temporal removes, depicts how a considered pursuit’s subjective value (green dots, y-intercept) would decrease as the time needed for its obtainment increases in environments that are otherwise the same. (C, D) Replotting the subjective values of the considered pursuit to correspond to their required delay forms the subjective value-time function for the ‘large’ reward case (C), and the ‘small’ reward case (D). (E) Normalizing the subjective value-time functions by their reward magnitude transforms these functions into their corresponding discounting functions (blue: large reward DF; red: small reward DF), and reveals that a reward-rate-maximizing agent would exhibit the ‘Magnitude Effect’ as the steepness of the apparent discounting function would change with the size of the pursuit, and manifest as being less steep the greater the magnitude of reward.
Figure 16
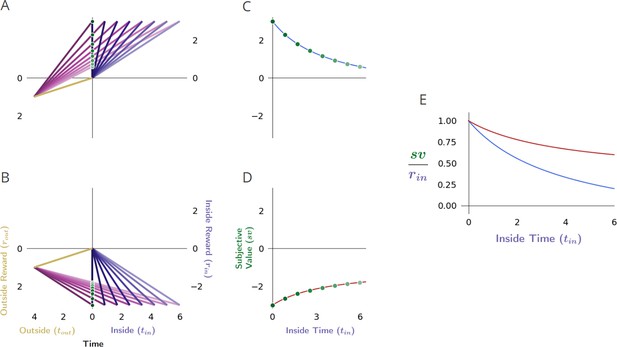
Reward-rate-maximizing agents would exhibit the ‘Sign effect’.
(A, B) The global reward rate (the slope of magenta lines) that would be obtained when acquiring a considered pursuit’s outcome of a given magnitude but differing in sign (either rewarding as in A, or punishing as in B), depicts how the subjective value (green dots, y-intercept) would decrease as the time of its obtainment increases in environments that are otherwise the same (one in which the agent spends the same amount of time and receives the same amount of reward outside the considered pursuit for every instance within it). (C, D) Replotting the subjective values of the considered pursuit to correspond to their required delay forms the subjective value-time function for the reward (C) and for the punishment (D). (E) Normalizing the subjective value-time functions by their outcome transforms these functions into their corresponding discounting functions (blue: reward DF; red: punishment DF). This reveals that a reward-rate-maximizing agent would exhibit the ‘Sign Effect’, as the steepness of the apparent discounting function would change with the sign of the pursuit, manifesting as being less steep for punishing than for rewarding outcomes of the same magnitude.
Figure 17
Relationship between outside time and reward with optimal temporal decision-making behavioral transitions.
An agent may be presented with three decisions: the decision to take or forgo a smaller, sooner reward of 2.5 units after 2.5 s (SS pursuit), the decision to take or forgo a larger, later reward of 5 units after 8.5 s (LL pursuit), and the decision to choose between the SS and LL pursuits. The slope of the purple line indicates the global reward rate (ρg) resulting from a Choice or Take policy, while the slope of ‘outside’ the pursuit (golden line) indicates the outside reward rate (i.e. global reward rate resulting from a Forgo policy). In each panel (A-D), an example outside reward rate is plotted, illustrating the relative ordering of ρg slopes for each policy. Location in the lower left quadrant is thereby shaded according to the combination of global rate-maximizing policies for each of the three decision types. rss = 2.5, tss = 2.5, rll = 5, tll = 8.5, tout = 6, rout = 0, 0.4, 0.8, 1.3 in A-D, respectively.
Figure 18
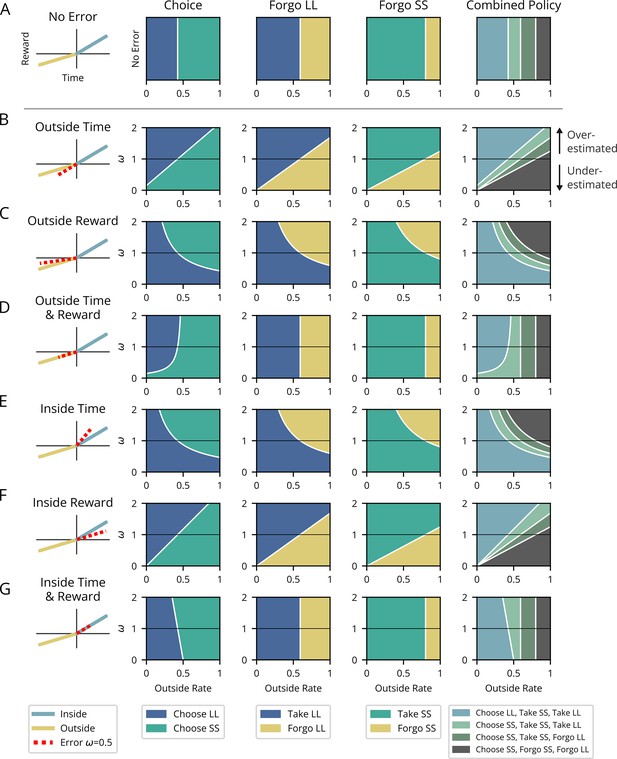
Patterns of suboptimal temporal decision-making behavior resulting from time and/or reward misestimation.
Patterns of temporal decision-making in Choice and Forgo situations deviate from optimal (top row) under various parameter misestimations (subsequent rows). Characterization of the nature of suboptimality is aided by the use of the outside reward rate as the independent variable influencing decision-making (x-axis), plotted against the degree of error (y-axis) of a given parameter (ω<1 underestimation, ω=1 actual, ω>1 overestimation). The leftmost column provides a schematic exemplifying true outside (gold) and inside (blue) pursuit parameters and the nature of parameter error (dashed red) investigated per row (all showing an instance of underestimation). For each error case, the agent’s resulting choice between SS and LL pursuits (2nd column), decision to take or forgo the LL pursuit (3rd column), and decision to take or forgo the SS pursuit (4th column) are indicated by the shaded color (legend, bottom of columns) for a range of outside rates and degrees of error. The rightmost column depicts the triplet of behavior observed, combined across tasks. Rows: (A) ‘No error’ - Optimal choice and forgo behavior. Vertical white lines show outside reward rate thresholds for optimal forgo behavior. (B-G) Suboptimal behavior resulting from parameter misestimation. (B-D) The impact of outside pursuit parameter misestimation. (B) ‘Outside Time’- The impact of misestimating outside time (and thus misestimating outside reward rate). (C) ‘Outside Reward’- The impact of misestimating outside reward (and thus misestimating outside reward rate). (D) ‘Outside Time and Reward’- The impact of misestimating outside time and reward, but maintaining outside reward rate. (E-G) The impact of inside pursuit parameter misestimation. (E) ‘Pursuit Time’- The impact of misestimating inside pursuit time and thus misestimating inside pursuit reward rate. (F) ‘Pursuit Reward’ - The impact of misestimating the pursuit reward (and thus misestimating the pursuit reward rate). (G) ‘Pursuit Time and Reward’ - The impact of misestimating the pursuit reward and time, but maintaining the pursuit’s reward rate. For this illustration, we determined the policies for a SS pursuit of 2 reward units after 2.5 s, a LL pursuit of 4.75 reward units after 8 s, and an outside time of 10 s. The qualitative shape of each region and resulting conclusions are general for all situations where the SS pursuit has a higher rate than the LL pursuit (and where a region exists where the optimal agent would choose LL at low outside rates).
Figure 19
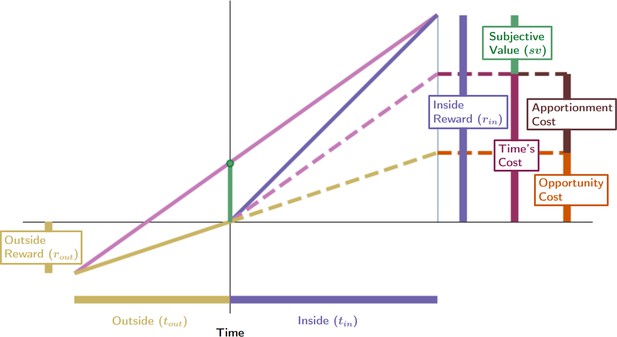
The cost of time of a pursuit comprises both an opportunity as well as an apportionment cost.
The global reward rate under a policy of accepting the considered pursuit type (slope of magenta time), times the time that pursuit takes (tin), is the pursuit’s time’s cost (height of maroon bar). The subjective value of a pursuit (height of green bar) is its reward magnitude (height of the purple bar) less its cost of time. Opportunity and apportionment costs are shown to compose the cost of time of a pursuit. Opportunity cost associated with a considered pursuit, ρout*tin, (height of orange bar) is the reward rate of the world under a policy of not accepting the considered pursuit (its outside rate), ρout, times the time of the considered pursuit, tin. Therefore, opportunity cost is the amount of reward that would be expected from a policy of not taking the considered pursuit over a time equal to the considered pursuit’s duration. The difference in reward that can be expected, on average, between a policy of taking versus a policy of not taking the considered pursuit, over a time equal to its duration, is the apportionment cost of time (height of brown bar). Together, they sum to time’s cost.
Figure 20
Comparison of typical hyperbolic discounting versus apparent discounting of a reward-rate-optimal agent.
Whereas (A) the curvature of hyperbolic discounting models is typically controlled by the free fit parameter k, (B) the curvature and steepness of the apparent discounting function of a reward-rate-optimal agent is controlled by the time spent and reward rate obtained outside the considered pursuit. Understanding the shape of discounting models from the perspective of a reward-rate-optimal agent reveals that k ought relate to the apportionment of time spent in, versus outside, the considered pursuit, underscoring, how typical hyperbolic discounting models fail to account for the opportunity cost of time (and thus cannot yield negative sv’s no matter the temporal displacement of reward). Should k be understood as representing time’s apportionment cost, the failure to account for the opportunity cost of time would lead to aberrantly high values of k.
Figure 21
The Malapportionment Hypothesis.
(A-E) Solid lines indicate true reward-rate maximizing values. Dashed lines indicate those of an agent described by the Malapportionment Hypothesis that underweights the apportionment of time outside relative to inside the considered pursuit type. The Malapportionment Hypothesis predicts the following: (A) Suboptimal Choice, Optimal Forgo. Suboptimally ‘mpatient’ decision-making, as revealed under Choice decision-making, arises in humans and animals as a consequence of the valuation process underweighting the contribution of accurately assessed pursuit reward rates outside versus inside the considered pursuit type. (Top Left) An example Choice situation where the global reward rate is maximized by choosing a larger later reward over a smaller-sooner reward. (Top Middle) An agent that underweights the outside time but accurately appreciates the outside and inside reward rates, overestimates the global reward rate resulting from each policy, and thus exhibits suboptimal impatience by selecting the smaller-sooner reward. = 0.3. (Top Right) Similarly, an agent that overweights the time inside the considered pursuit but accurately appreciates the outside and inside reward rates also overestimates the global reward rate and selects the smaller-sooner reward. As inside and outside reward rates are accurately assessed, forgo decisions can correctly be made despite any misappreciation of the relative time spent in/outside the considered pursuit. = 1.8. (B) Hyperbolic discounting with greater curvature. The Malapportionment Hypothesis predicts that humans and animals exhibit temporal discounting with greater curvature than a reward-rate maximizing agent. = 0.5, rin = 5, rout = 0.5, tout = 5. (C) Less pronounced Magnitude Effect. The Malapportionment Hypothesis predicts that the difference in apparent discounting related to the magnitude of the pursuit will be less pronounced than a reward-rate-maximizing agent. = 0.5, rout = 0.5, tout = 5, rSS = 2, rLL = 5. (D) Less pronounced Sign Effect. The Sign Effect is also predicted to be less pronounced than a reward-rate-maximizing agent. = 0.5, rout = 0.5, tout = 5, positive reward = 3, negative reward (punishment) = –3. (E) More pronounced Delay Effect. The Malapportionment Hypothesis predicts that the Delay Effect will be more pronounced than that exhibited by a reward-rate-maximizing agent. = 0.5, rout = 0.5, tout = 5, rSS = 2, tSS = 3, rLL = 5, tLL = 12.6.
Tables
Table 1
Definitions for misestimating global reward rate-enabling parameters.
Each misestimated variable (column 1) is multiplied by an error term, , to give , the misestimated global reward rate (column 2). When the variable is underestimated, when the variable is overestimated, and when the variable is correctly estimated and .
| Misestimated Variable | Misestimated Global Reward Rate |
|---|---|
| True (No Misestimation) | |
| Outside Time | |
| Outside Reward | |
| Outside Time and Reward (maintaining ) | |
| Inside Time | |
| Inside Reward | |
| Inside Reward and Time (maintaining ) |
Table 2
Opportunity cost, apportionment cost, time cost, and subjective value functions by change in outside and inside reward and time.
Functions assume positive inside and outside rewards and times.
| Reward | Time | |||
|---|---|---|---|---|
| Outside | Inside | Outside | Inside | |
| Opportunity Cost* | Linear Positive slope | No Effect | Hyperbolic Negative slope | Linear Positive slope |
| Apportionment Cost | Linear Negative slope | Linear Positive slope | Hyperbolic - Hyperbolic† Negative slope | Hyperbolic - Linear† Negative slope |
| Time’s Cost | Linear Positive slope | Linear Positive slope | Hyperbolic Negative slope | Hyperbolic Positive slope |
| Subjective Value | Linear Negative slope | Linear Positive slope | Hyperbolic Positive Slope | Hyperbolic Negative slope |
-
*
If outside reward rate is zero, opportunity cost becomes a constant at zero.
-
†
If outside reward rate is zero, as outside or inside time is varied, apportionment cost becomes purely hyperbolic.
Additional files
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The value of initiating a pursuit in temporal decision-making
eLife 13:RP99957.
https://doi.org/10.7554/eLife.99957.3
