From multiplicity of infection to force of infection for sparsely sampled Plasmodium falciparum populations at high transmission

Reviewer #1 (Public review):

Summary

In their paper Zhan et al. have used Pf genetic data from simulated data and Ghanaian field samples to elucidate a relationship between multiplicity of infection (MOI) (the number of distinct parasite clones in a single host infection) and force of infection (FOI). Specifically, they use sequencing data from the var genes of Pf along with Bayesian modeling to estimate MOI individual infections and use these values along with methods from queueing theory that rely on various assumptions to estimate FOI. They compare these estimates to known FOIs in a simulated scenario and describe the relationship between these estimated FOI values and another commonly used metric of transmission EIR (entomological inoculation rate).

This approach does fill an important gap in malaria epidemiology, namely estimating force of infection, which is currently complicated by several factors including superinfection, unknown duration of infection, and highly genetically diverse parasite populations. The authors use a new approach borrowing from other fields of statistics and modeling and make extensive efforts to evaluate their approach under a range of realistic sampling scenarios. However, the write-up would greatly benefit from added clarity both in the description of methods, and in the presentation of the results. Without these clarifications, rigorously evaluating whether the author's proposed method of estimating FOI is sound remains difficult. Additionally, there are several limitations that call into question the stated generalizability of this method that should at minimum be further discussed by authors and in some cases require a more thorough evaluation.

Major comments:

(1) Description and evaluation of FOI estimation procedure.

a. The methods section describing the two-moment approximation and accompanying appendix is lacking several important details. Equations on line 891 and 892 are only a small part of the equations in Choi et al. and do not adequately describe the procedure notably several quantities in those equations are never defined some of them are important to understand the method (e.g. A, S as the main random variables for inter-arrival times and service times, aR and bR which are the known time average quantities, and these also rely on the squared coefficient of variation of the random variable which is also never introduced in the paper). Without going back to the Choi paper to understand these quantities, and to understand the assumptions of this method it was not possible to follow how this works in the paper. At minimum, all variables used in the equations should be clearly defined.

b. Additionally, the description in the main text of how queueing procedure can be used to describe malaria infections would benefit from a diagram currently as written it's very difficult to follow.

c. Just observing the box plots of mean and 95% CI on a plot with the FOI estimate (Figures 1, 2 and 10-14) is not sufficient to adequately assess the performance of this estimator. First, it is not clear whether authors are displaying the bootstrapped 95%Cis or whether they are just showing the distribution of the mean FOI taken over multiple simulations, and then it seems that they are also estimating mean FOI per host on an annual basis. Showing a distribution of those per host estimates would also be helpful. Second, a more quantitative assessment of the ability of the estimator to recover the truth across simulations (e.g. proportion of simulations where the truth is captured in the 95% CI or something like this) is important in many cases it seems that the estimator is always underestimating the true FOI and may not even contain the true value in the FOI distribution (e.g. figure 10, figure 1 under the mid IRS panel). But it's not possible to conclude on way or the other based on this visualization. This is a major issue since it calls into question whether there is in fact data to support that these methods give good and consistent FOI estimates.

d. Furthermore authors state in the methods that the choice of mean and variance (and thus second moment) parameters for inter arrival times are varied widely, however, it's not clear what those ranges are there needs to be a clear table or figure caption showing what combinations of values were tested and which results are produced from them, this is an essential component of the method and it's impossible to fully evaluate its performance without this information. This relates to the issue of selecting the mean and variance values that maximize the likelihood of observing a given distribution of MOI estimates, this is very unclear since no likelihoods have been written down in the methods section of the main text, which likelihood are the authors referring to, is this the probability distribution of the steady state queue length distribution? At other places the authors refer to these quantities as Maximum Likelihood estimators, how do they know they have found the MLE? There are no derivations in the manuscript to support this. The authors should specify and likelihood and include in an appendix why their estimation procedure is in fact maximizing this likelihood preferably with evidence of the shape of the likelihood, and how fine the grid of values they tested are for their mean and variance since this could influence the overall quality of the estimation procedure.

(2) Limitation of FOI estimation procedure.

a. The authors discuss the importance of duration of infection to this problem. While I agree that empirically estimating this is not possible, there are other options besides assuming that all 1-5 year olds have the same duration of infection distribution as naïve adults co-infected with syphilis. E.g. it would be useful to test a wide range of assumed infection duration and assess their impact on the estimation procedure. Furthermore, if the authors are going to stick to the described method for duration of infection, the potentially limited generalizability of this method needs to be further highlighted in both the introduction, and the discussion. In particular, for an estimated mean FOI of about 5 per host per year in the pre-IRS season as estimated in Ghana (Figure 3) it seems that this would not translate to 4 year old being immune naïve, and certainly this would not necessarily generalize well to a school-aged child population or an adult population.

b. The evaluation of the capacity parameter c seems to be quite important, and is set at 30, however, the authors only describe trying values of 25 and 30, and claim that this does not impact FOI inference, however it is not clear that this is the case. What happens if carrying capacity is increased substantially? Alternatively, this would be more convincing if the authors provided a mathematical explanation of why the carrying capacity increasing will not influence the FOI inference, but absent that, this should be mentioned and discussed as a limitation.

Comments on revisions:

The authors have adequately responded to all comments.

Reviewer #2 (Public review):

Summary:

The authors combine a clever use of historical clinical data on infection duration in immunologically naive individuals and queuing theory to infer the force of infection (FOI) from measured multiplicity of infection (MOI) in a sparsely sampled setting. They conduct extensive simulations using agent based modeling to recapitulate realistic population dynamics and successfully apply their method to recover FOI from measured MOI. They then go on to apply their method to real world data from Ghana before and after an indoor residual spraying campaign.

Strengths:

- The use of historical clinical data is very clever in this context
- The simulations are very sophisticated with respect to trying to capture realistic population dynamics
- The mathematical approach is simple and elegant, and thus easy to understand

Weaknesses:

- The assumptions of the approach are quite strong, and the authors have made clear that applicability is constrained to individuals with immune profiles that are similar to malaria naive patients with neurosyphilis. While the historical clinical data is a unique resource and likely directionally correct, it remains somewhat dubious to use the exact estimated values as inputs to other models without extensive sensitivity analysis.

Reviewer #3 (Public review):

Summary:

It has been proposed that the FOI is a method of using parasite genetics to determine changes in transmission in areas with high asymptomatic infection. The manuscript attempts to use queuing theory to convert multiplicity of infection estimates (MOI) into estimates of the force of infection (FOI), which they define as the number of genetically distinct blood-stage strains. They look to validate the method by applying them to simulated results from a previously published agent based model. They then apply these queuing theory methods to previously published and analysed genetic data from Ghana. They then compare their results to previous estimates of FOI.

Strengths:

It would be great to be able to infer FOI from cross sectional surveys which are easier and cheaper than current FOI estimates which require longitudinal studies. This work proposes a method to convert MOI to FOI for cross sectional studies. They attempt to validate this process using a previously published agent based model which helps us understand the complexity of parasite population genetics.

Weaknesses:

(1) I fear that the work could be easily over-interpreted as no true validation was done as no field estimates of FOI (I think considered true validation) were measured. You have developed a method of estimating FOI from MOI which makes a number of biological and structural assumptions. I would not call being able to recreate model results that were generated using a model that makes its own (probably similar) defined set of biological and structural assumptions acts as a validation of what is going on in the field. The authors claim this at times (for example, Line 153 ) and I feel it would be appropriate to differentiate this in the discussion.

(2) Another aspect of the paper is adding greater realism to the previous agent based model, by including assumptions on missing data and under sampling. This takes prominence in the figures and results section, but I would imagine is generally not as interesting to the less specialised reader. The apparent lack of impact of drug treatment on MOI is interesting and counterintuitive, though it is not really mentioned in the results or discussion sufficiently to allay my confusion. I would have been interested in understanding the relationship between MOI and FOI as generated by your queuing theory method and the model. It isn't clear to me why these more standard results are not presented, as I would imagine they are outputs of the model (though happy to stand corrected - it isn't entirely clear to me what the model is doing in this manuscript alone).

(3) I would suggest that outside of malaria geneticists, the force of infection is considered to be the entomological inoculation rate, not the number of genetically distinct blood-stage strains. I appreciate that FOI has been used to explain the later before by others, though the authors could avoid confusion by stating this clearly throughout the manuscript. For example, the abstract says FOI is "the number of new infections acquired by an individual host over a given time interval" which suggests the former, please consider clarifying.

(4) Line 319 says "Nevertheless, overall, our paired EIR (directly measured by the entomological team in Ghana (Tiedje et al., 2022)) and FOI values are reasonably consistent with the data points from previous studies, suggesting the robustness of our proposed methods". I would agree that the results are consistent, given that there is huge variation in Figure 4 despite the transformed scales, but I would not say this suggests a robustness of the method.

(5) The text is a little difficult to follow at times, and sometimes requires multiple reads to understand. Greater precision is needed with the language in a few situations and some of the assumptions made in the modelling process are not referenced, making it unclear whether it is a true representation of the biology.

Comments on revisions:

I think the authors gave a robust but thorough response to our reviews and made some important changes to the manuscript which certainly clarify things for me.

Author response:

The following is the authors’ response to the original reviews

Public Reviews:

Reviewer #1 (Public Review):

Summary:

In their paper, Zhan et al. have used Pf genetic data from simulated data and Ghanaian field samples to elucidate a relationship between multiplicity of infection (MOI) (the number of distinct parasite clones in a single host infection) and force of infection (FOI). Specifically, they use sequencing data from the var genes of Pf along with Bayesian modeling to estimate MOI individual infections and use these values along with methods from queueing theory that rely on various assumptions to estimate FOI. They compare these estimates to known FOIs in a simulated scenario and describe the relationship between these estimated FOI values and another commonly used metric of transmission EIR (entomological inoculation rate).

This approach does fill an important gap in malaria epidemiology, namely estimating the force of infection, which is currently complicated by several factors including superinfection, unknown duration of infection, and highly genetically diverse parasite populations. The authors use a new approach borrowing from other fields of statistics and modeling and make extensive efforts to evaluate their approach under a range of realistic sampling scenarios. However, the write-up would greatly benefit from added clarity both in the description of methods and in the presentation of the results. Without these clarifications, rigorously evaluating whether the author's proposed method of estimating FOI is sound remains difficult. Additionally, there are several limitations that call into question the stated generalizability of this method that should at minimum be further discussed by authors and in some cases require a more thorough evaluation.

Major comments:

(1) Description and evaluation of FOI estimation procedure.

a. The methods section describing the two-moment approximation and accompanying appendix is lacking several important details. Equations on lines 891 and 892 are only a small part of the equations in Choi et al. and do not adequately describe the procedure notably several quantities in those equations are never defined some of them are important to understand the method (e.g. A, S as the main random variables for inter-arrival times and service times, aR and bR which are the known time average quantities, and these also rely on the squared coefficient of variation of the random variable which is also never introduced in the paper). Without going back to the Choi paper to understand these quantities, and to understand the assumptions of this method it was not possible to follow how this works in the paper. At a minimum, all variables used in the equations should be clearly defined.

We thank the reviewer for this useful comment. We have clarified the method and defined all relevant variables in the revised manuscript (Line 537-573). The reviewer correctly pointed out additional sections and equations in Choi et al., including the derivation of an exact expression for the steady-state queue-length distribution and the two-moment approximation. Since our work directly utilized the two-moment approximation, our previous manuscript included only material on that section. However, we agree that providing additional details on the derivation of the exact expression would benefit readers. Therefore, we have summarized this derivation in the revised manuscript (Line 561-564). Additionally, we clarified the method’s assumptions, particularly those involved in transitioning from the exact expression to the two-moment approximation (Line 565-570).

b. Additionally, the description in the main text of how the queueing procedure can be used to describe malaria infections would benefit from a diagram currently as written it's very difficult to follow.

We thank the reviewer for this suggestion. In the revised manuscript, we included a diagram illustrating the connection between the queueing procedure and malaria transmission (Appendix 1-Figure 8).

c. Just observing the box plots of mean and 95% CI on a plot with the FOI estimate (Figures 1, 2, and 10-14) is not sufficient to adequately assess the performance of this estimator. First, it is not clear whether the authors are displaying the bootstrapped 95%CIs or whether they are just showing the distribution of the mean FOI taken over multiple simulations, and then it seems that they are also estimating mean FOI per host on an annual basis. Showing a distribution of those per-host estimates would also be helpful. Second, a more quantitative assessment of the ability of the estimator to recover the truth across simulations (e.g. proportion of simulations where the truth is captured in the 95% CI or something like this) is important in many cases it seems that the estimator is always underestimating the true FOI and may not even contain the true value in the FOI distribution (e.g. Figure 10, Figure 1 under the mid-IRS panel). But it's not possible to conclude one way or the other based on this visualization. This is a major issue since it calls into question whether there is in fact data to support that these methods give good and consistent FOI estimates.

There seems to be some confusion on what we display in some key figures. Figures 1-2 and 10-14 (labeled as Figure 1-2 and Appendix 1-Figure 11-15 in the revised manuscript) display bootstrapped distributions including the 95% CIs, not the distribution of the mean FOI taken over multiple simulations. To estimate the mean FOI per host on an annual basis, the two proposed methods require either the steady-state queue length distribution (MOI distribution) or the moments of this distribution. Obtaining such a steady-state queue length distribution necessitates either densely tracked time-series observations per host or many realizations at the same sampling time per host. However, under the sparse sampling schemes, we only have two one-time-point observations per host: one at the end of wet/high-transmission and another at the end of dry/low-transmission. This is typically the case for empirical data, although numerical simulations could circumvent this limitation and generate such output. Nonetheless, we have a population-level queue length distribution from both simulation outputs and empirical data by aggregating MOI estimates across all sampled individuals. We use this population-level distribution to represent and approximate the steady-state queue length distribution at the individual level, not explicitly considering any individual heterogeneity due to transmission. The estimated FOI is per host in the sense of representing the FOI experienced by an individual host whose queue length distribution is approximated from the collection of all sampled individuals. The true FOI per host per year in the simulation is the total FOI of all hosts per year divided by the number of hosts. Therefore, our estimator, combined with the demographic information on population size, estimates the total number of Plasmodium falciparum infections acquired by all individual hosts in the population of interest per year. We clarified this point in the revised manuscript in the subsection of the Materials and Methods, entitled ‘Population-level MOI distribution for approximating time-series observation of MOI per host or many realizations at the same sampling time per host’ (Line 623-639).

We evaluated the impact of individual heterogeneity due to transmission on FOI inference using simulation outputs (Line 157-184, Figure 1-2 and Appendix 1-Figure 11-15). Even with significant heterogeneity among individuals (2/3 of the population receiving approximately 94% of all bites whereas the remaining 1/3 receives the rest of the bites), our methods performed comparably to scenarios with homogeneous transmission. Furthermore, our methods demonstrated similar performance for both non-seasonal and seasonal transmission scenarios.

Regarding the second point, we quantitatively assessed the ability of the estimator to recover the truth across simulations and included this information in a supplementary table in the revised manuscript (supplementary file 3-FOImethodsPerformance.xlsx). Specifically, we indicated whether the truth lies within the bootstrap distribution and provided a measure of relative deviation, which is defined as the true FOI value minus the median of the bootstrap distribution for the estimate, normalized by the true FOI value 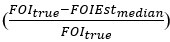. This assessment is a valuable addition which enhances clarity, but please note that our previous graphical comparisons do illustrate the ability of the methods to estimate “sensible” values, close to the truth despite multiple sources of errors. “Close” here is relative to the scale of variation of FOI in the field and to the kind of precision that would be useful in an empirical context. From a practical perspective based on the potential range of variation of FOI, the graphical results already illustrate that the estimated distributions would be informative.

We also thank the reviewer for highlighting instances where our proposed methods for FOI inference perform sub-optimally (e.g. Figure 10, Figure 1 under the mid-IRS panel in the previous manuscript). This feedback prompted us to examine these instances more closely and identify the underlying causes related to the stochastic impact introduced during various sampling processes. These include sampling the host population and their infections at a specific sampling depth in the simulated output, matching the depth used for collecting empirical data. In addition, previously, we imputed MOI estimates for treated individuals by sampling only once from non-treated individuals. This time, we conducted 200 samplings and used the final weighted MOI distribution for FOI inference. By doing so, we reduced the impact of extreme single-sampling efforts on MOI distribution and FOI inference. In other words, some of these suboptimal instances correspond to the scenarios where the one-time sampled MOIs from non-treated individuals do not fully capture the MOI distribution of non-treated individuals. We added a section titled ‘Reducing stochastic impact in sampling processes’ to Appendix 1 on this matter (Line 841-849).

The reviewer correctly noted that our proposed methods tend to underestimate FOI (Figure 1-2, 10-14, ‘Estimated All Errors’ and ‘Estimated Undersampling of Var’ panels in the previous manuscript, corresponding to Figure 1-2 and Appendix 1-Figure 11-15 in the revised manuscript). This underestimation arises from the underestimation of MOI. The Bayesian formulation of the varcoding method does not account for the limited overlap between co-infecting strains, an additional factor that reduces the number of var genes detected per individual. We have elaborated on this matter in the Results and Discussion sections of the revised manuscript (Line 142-149, 252-256).

d. Furthermore the authors state in the methods that the choice of mean and variance (and thus second moment) parameters for inter-arrival times are varied widely, however, it's not clear what those ranges are there needs to be a clear table or figure caption showing what combinations of values were tested and which results are produced from them, this is an essential component of the method and it's impossible to fully evaluate its performance without this information. This relates to the issue of selecting the mean and variance values that maximize the likelihood of observing a given distribution of MOI estimates, this is very unclear since no likelihoods have been written down in the methods section of the main text, which likelihood are the authors referring to, is this the probability distribution of the steady state queue length distribution? At other places the authors refer to these quantities as Maximum Likelihood estimators, how do they know they have found the MLE? There are no derivations in the manuscript to support this. The authors should specify the likelihood and include in an appendix an explanation of why their estimation procedure is in fact maximizing this likelihood, preferably with evidence of the shape of the likelihood, and how fine the grid of values they tested is for their mean and variance since this could influence the overall quality of the estimation procedure.

We thank the reviewer for pointing out these aspects of the work that can be further clarified. In response, we maximized the likelihood of observing the population-level MOI distribution in the sampled population (see our responses to your previous comment c), given queue length distributions, derived from the two-moment approximation method for various mean and variance combinations of inter-arrival times. We added a new section to the Materials and Methods in the revised manuscript with an explicit likelihood formulation (Line 574-585).

Additionally, we specified the ranges for the mean and variance parameters for inter-arrival times and provided the grid of values tested in a supplementary table (supplementary file 4-meanVarianceParams.xlsx). Example figures illustrating the shape of the likelihood have also been included in Appendix 1-Figure 9. We tested the impact of different grid value choices on estimation quality by refining the grid to include more points, ensuring the FOI inference results are consistent. The results of the test are documented in the revised manuscript (Line 587-593, Appendix 1-Figure 10).

(2) Limitation of FOI estimation procedure.

a. The authors discuss the importance of the duration of infection to this problem. While I agree that empirically estimating this is not possible, there are other options besides assuming that all 1-5-year-olds have the same duration of infection distribution as naïve adults co-infected with syphilis. E.g. it would be useful to test a wide range of assumed infection duration and assess their impact on the estimation procedure. Furthermore, if the authors are going to stick to the described method for duration of infection, the potentially limited generalizability of this method needs to be further highlighted in both the introduction, and the discussion. In particular, for an estimated mean FOI of about 5 per host per year in the pre-IRS season as estimated in Ghana (Figure 3) it seems that this would not translate to 4-year-old being immune naïve, and certainly this would not necessarily generalize well to a school-aged child population or an adult population.

We thank the reviewer for this useful comment. The reviewer correctly noted the challenge in empirically measuring the duration of infection for 1-5-year-olds and comparing it to that of naïve adults co-infected with syphilis. We nevertheless continued to use the described method for the duration of infection, while more thoroughly acknowledging and discussing the limitations this aspect of the method introduces. We have highlighted this potential limitation in the Abstract, Introduction, and Discussion sections of the revised manuscript (Line 26-28, 99-103, 270-292). It is important to note that the infection duration from the historical clinical data we have relied on has been used, and is still used, in the malaria modeling community as a credible source for this parameter in untreated natural infections of malaria-naïve individuals in endemic settings of Africa (e.g. in the agent-based model OpenMalaria, see 1).

To reduce misspecification in infection duration and fully utilize our proposed methods, future data collection and sampling could prioritize subpopulations with minimal prior infections and an immune profile similar to naïve adults, such as infants and toddlers. As these individuals are also the most vulnerable, prioritizing them aligns with the priority of all intervention efforts in the short term, which is to monitor and protect the most vulnerable individuals from severe symptoms and death. We discuss this aspect in detail in the Discussion section of the revised manuscript (Line 287-292).

In the pre-IRS phase of Ghana surveys, an estimated mean FOI of about 5 per host per year indicates that a 4-year-old child would have experienced around 20 infections, which could suggest they are far from naïve. The extreme diversity of circulating var genes (2) implies, however, that even after 20 infections, a 4-year-old may have only developed immunity to a small fraction of the variant surface antigens (PfEMP1, Plasmodium falciparum erythrocyte membrane protein 1) encoded by this important gene family. Consequently, these children are not as immunologically experienced as it might initially seem. Moreover, studies have shown that long-lived infections in older children and adults can persist for months or even years, including through the dry season. This persistence is driven by high antigenic variation of var genes and associated incomplete immunity. Additionally, parasites can skew PfEMP1 expression to produce less adhesive erythrocytes, enhancing splenic clearance, reducing virulence, and maintaining sub-clinical parasitemia (3, 4, 5). The impact of immunity on infection duration with age for falciparum malaria remains a challenging open question.

Lastly, the FOI for naïve hosts is a key basic parameter for epidemiological models of complex infectious diseases like falciparum malaria, in both agent-based and equation-based formulations. This is because FOI for non-naïve hosts is typically a function of their immune status, body size, and the FOI of naïve hosts. Thus, knowing the FOI of naïve hosts helps parameterize and validate these models by reducing degrees of freedom.

b. The evaluation of the capacity parameter c seems to be quite important and is set at 30, however, the authors only describe trying values of 25 and 30, and claim that this does not impact FOI inference, however it is not clear that this is the case. What happens if the carrying capacity is increased substantially? Alternatively, this would be more convincing if the authors provided a mathematical explanation of why the carrying capacity increase will not influence the FOI inference, but absent that, this should be mentioned and discussed as a limitation.

Thank you for this question. This parameter represents the carrying capacity of the queuing system, or the maximum number of blood-stage strains with which an individual human host can be co-infected. Empirical evidence, estimated using the varcoding method, suggests this value is 20 (2), providing a lower bound for parameter c. However, the varcoding method does not account for the limited overlap between co-infecting strains, which reduces the number of var genes detected in an individual, thereby affecting the basis of MOI estimation. Additional factors, such as the synchronicity of clones in their 48-hour life cycle on alternate days (6) and within-host competition of strains leading to low-parasitemia levels (7, 8), contribute to under-sampling of strains and are not accounted for in MOI estimation (9). To address these potential under-sampling issues, we previously tested values of 25 and 30.

This time, we systematically investigated a wider range of values, including substantially higher ones: 25, 30, 40, and 60. We found that the FOI inference results are similar across these values. Figure 3 in the main text and supplementary figures (Appendix 1-Figure 16-18) illustrates these findings.

The parameter c influences the steady-state queue length distribution based on the two-moment approximation with specific mean and variance combinations, primarily affecting the distribution’s tail when customer or infection flows are high. Smaller values of c lower the maximum possible queue length, making the system more prone to “overflow”. In such cases, customers or infections may find no space available upon their arrival, hence not incrementing the queue length.

Empirical MOI distributions for high-transmission endemic regions center around 4 or 5, mostly remaining below 10, with only a small fraction between 15-20 (2). These distributions do not support parameter combinations resulting in frequent overflow for a system with c equal to 25 or 30. As one increases the value of c further, these parameter combinations would cause the MOI distributions to shift to larger values inconsistent with the empirical MOI distributions. We therefore do not expect substantially higher values for parameter c to noticeably change either the relative shape of the likelihood or the MLE.

We have included a subsection on parameter c in the Materials and Methods section of the revised manuscript (Line 596-612).

Reviewer #2 (Public Review):

Summary:

The authors combine a clever use of historical clinical data on infection duration in immunologically naive individuals and queuing theory to infer the force of infection (FOI) from measured multiplicity of infection (MOI) in a sparsely sampled setting. They conduct extensive simulations using agent-based modeling to recapitulate realistic population dynamics and successfully apply their method to recover FOI from measured MOI. They then go on to apply their method to real-world data from Ghana before and after an indoor residual spraying campaign.

Strengths:

(1) The use of historical clinical data is very clever in this context.

(2) The simulations are very sophisticated with respect to trying to capture realistic population dynamics.

(3) The mathematical approach is simple and elegant, and thus easy to understand.

Weaknesses:

(1) The assumptions of the approach are quite strong and should be made more clear. While the historical clinical data is a unique resource, it would be useful to see how misspecification of the duration of infection distribution would impact the estimates.

We thank the reviewer for bringing up the limitation of our proposed methods due to their reliance on a known and fixed duration of infection distribution from historical clinical data. Please see our response to Reviewer 1, Comment 2a, for a detailed discussion on this matter.

(2) Seeing as how the assumption of the duration of infection distribution is drawn from historical data and not informed by the data on hand, it does not substantially expand beyond MOI. The authors could address this by suggesting avenues for more refined estimates of infection duration.

We thank the reviewer for pointing out a potential improvement to our work. We acknowledge that FOI is inferred from MOI and thus depends on the information contained in MOI. However, MOI by definition is a number and not a rate parameter. FOI for naïve hosts is a fundamental parameter for epidemiological models of complex infectious diseases like falciparum malaria, in both agent-based and equation-based formulations. FOI of non-naïve hosts is typically a function of their immune status, body size, and the FOI of naïve hosts. Thus, knowing the FOI of naïve hosts helps parameterize and validate these models by reducing degrees of freedom. In this sense, we believe the transformation from MOI to FOI is valuable.

Measuring infection duration is challenging, making the simultaneous estimation of infection duration and FOI an attractive alternative, as the referee noted. This, however, would require closely monitored cohort studies or densely sampled cross-sectional surveys to reduce issues like identifiability. For instance, a higher arrival rate of infections paired with a shorter infection duration could generate a similar MOI distribution to a lower arrival rate with a longer infection duration. In some cases, incorrect combinations of rate and duration might even produce an MOI distribution that appears closer to the targeted distribution. Such cohort studies and densely sampled cross-sectional surveys have not been and will not be widely available across different geographical locations and times. This work utilizes more readily available data from sparsely sampled single-time-point cross-sectional surveys, which precludes more sophisticated derivation of time-varying average arrival rates of infections and lacks the resolution to simultaneously estimate arrival rates and infection duration. In the revised manuscript, we have elaborated on this matter and added a paragraph in the Discussion section (Line 306-309).

(3) It is unclear in the example how their bootstrap imputation approach is accounting for measurement error due to antimalarial treatment. They supply two approaches. First, there is no effect on measurement, so the measured MOI is unaffected, which is likely false and I think the authors are in agreement. The second approach instead discards the measurement for malaria-treated individuals and imputes their MOI by drawing from the remaining distribution. This is an extremely strong assumption that the distribution of MOI of the treated is the same as the untreated, which seems unlikely simply out of treatment-seeking behavior. By imputing in this way, the authors will also deflate the variability of their estimates.

We thank the reviewer for pointing out aspects of the work that can be further clarified. Disentangling the effect of drug treatment on measurements like infection duration is challenging. Since our methods rely on the known and fixed distribution of infection duration from historical data of naïve patients with neurosyphilis infected with malaria as a therapy, drug treatment can potentially violate this assumption. In the previous manuscript, we did not attempt to directly address the impact of drug treatment. Instead, we considered two extreme scenarios that bound reality, well summarized by the reviewer. Reality lies somewhere in between these two extremes, with antimalarial treatment significantly affecting measurements in some individuals but not in others. Nonetheless, the results of FOI inference do not differ significantly across both extremes.

The impact of the drugs likely depends on their nature, efficiency, and duration. We note that treatment information was collected via a routine questionnaire, with participant self-reporting that they had received an antimalarial treatment in the previous two-weeks before the surveys (i.e., participants that reported they were sick, sought treatment, and were provided with an antimalarial treatment). No confirmation through hospital or clinic records was conducted, as it was beyond the scope of the study. Additionally, many of these sick individuals seek treatment at local chemists, which may limit the relevance of hospital or clinic records, if they are even available. Consequently, information on the nature, efficiency, and duration of administrated drugs was incomplete or lacking. As this is not the focus of this work, we do not elaborate on the impact of drug treatment in the revised manuscript.

The reviewer correctly noted that this imputation might not add additional information and could reduce MOI variability. Therefore, in the revised manuscript, we reported FOI estimates with drug-treated 1-5-year-olds excluded. Additionally, we discarded the infection status and MOI values of treated individuals and sampled their MOI from non-treated microscopy-positive individuals, imputing a positive MOI for treated and uninfected individuals. We also reported FOI estimates based on these MOI values. This scenario provides an upper bound for FOI estimates. Note that we do not assume that the MOI distribution for treated individuals is the same as that for untreated individuals. Rather, we aim to estimate what their MOI would have been, and consequently, determine what the FOI per individual per year in the combined population would be, had these individuals not received antimalarial treatment. The results of FOI inference do not differ significantly between these two approaches. They can serve as general solutions to antimalarial treatment issues for others applying our FOI inference methods. These details can be found in the revised manuscript (Line 185-210, 462-484).

- For similar reasons, their imputation of microscopy-negative individuals is also questionable, as it also assumes the same distributions of MOI for microscopy-positive and negative individuals.

We thank the reviewer for this comment. The reviewer correctly noted that we imputed the MOI values for microscopy-negative but PCR-positive 1-5-year-olds by sampling from the microscopy-positive 1-5-year-olds, under the assumption that both groups have similar MOI distributions. This approach was motivated by the analysis of our Ghana surveys, which shows no clear relationship between MOI (or the number of var genes detected within an individual host, on the basis of which our MOI values were estimated) and the parasitemia levels of those hosts. Parasitemia levels underlie the difference in detection sensitivity between PCR and microscopy.

In the revised manuscript, we elaborated on this issue and included formal regression tests showing the lack of a relationship between MOI/the number of var genes detected within an individual host and the parasitemia levels of those hosts (Line 445-451, Appendix 1-Figure 7). We also described potential reasons or hypotheses behind this observation (Line 452-461).

Reviewer #3 (Public Review):

Summary:

It has been proposed that the FOI is a method of using parasite genetics to determine changes in transmission in areas with high asymptomatic infection. The manuscript attempts to use queuing theory to convert multiplicity of infection estimates (MOI) into estimates of the force of infection (FOI), which they define as the number of genetically distinct blood-stage strains. They look to validate the method by applying it to simulated results from a previously published agent-based model. They then apply these queuing theory methods to previously published and analysed genetic data from Ghana. They then compare their results to previous estimates of FOI.

Strengths:

It would be great to be able to infer FOI from cross-sectional surveys which are easier and cheaper than current FOI estimates which require longitudinal studies. This work proposes a method to convert MOI to FOI for cross-sectional studies. They attempt to validate this process using a previously published agent-based model which helps us understand the complexity of parasite population genetics.

Weaknesses:

(1) I fear that the work could be easily over-interpreted as no true validation was done, as no field estimates of FOI (I think considered true validation) were measured. The authors have developed a method of estimating FOI from MOI which makes a number of biological and structural assumptions. I would not call being able to recreate model results that were generated using a model that makes its own (probably similar) defined set of biological and structural assumptions a validation of what is going on in the field. The authors claim this at times (for example, Line 153) and I feel it would be appropriate to differentiate this in the discussion.

We thank the reviewer for this comment, although we think there is a mis-understanding on what can and cannot be practically validated in the sense of a “true” measure of FOI that would be free from assumptions for a complex disease such as malaria. We would not want the results to be over-interpreted, and we have extended the discussion of what we have done to test the methods in the revised manuscript (Line 314-328). Performance evaluation via simulation output is common and often necessary for statistical methods. These simulations can come from dynamical or descriptive models, each making their own assumptions to simplify reality. Our stochastic agent-based model (ABM) of malaria transmission, used in this study, has successfully replicated several key patterns from high-transmission endemic regions in the field, including aspects of strain diversity not represented and captured by simpler models (10).

In what sense this ABM makes a set of biological and structural assumptions that are “probably similar” to those of the queuing methods we present is not clear to us. We agree that using models with different structural assumptions from the method being tested is ideal. Our FOI inference methods based on queuing theory require the duration of infection distribution and the MOI distribution among sampled individuals. However, these FOI inference methods are agnostic to the specific biological mechanisms governing these distributions.

Another important point raised by this comment is what would be the “true” FOI value against which to validate our methods. Empirical MOI-FOI pairs from cohort studies tracking FOI directly are still lacking. Direct FOI measurements are prone to errors because differentiating new infections from the temporary absence of an old infection in the peripheral blood and its subsequent re-emergence remains challenging. Reasons for this challenge include the low resolution of the polymorphic markers used in cohort studies, which cannot fully differentiate hyper-diverse antigenic strains, and the complexity of within-host dynamics and competitive interaction of co-infecting strains (6, 8, 9). Alternative approaches also do not provide a “true” FOI estimation free from assumptions. These approaches involve fitting simplified epidemiological models to densely sampled/repeated cross-sectional surveys for FOI inference. In this case, no FOI is measured directly, and thus, there are no FOI values available for benchmarking against fitted FOI values. The evaluation or validation of these model-fitting approaches is typically based on their ability to capture other epidemiological quantities that are easier to sample or measure, such as prevalence or incidence, with criteria such as the Akaike information criterion (AIC). This type of evaluation is similar to the one done in this work. We selected FOI values that maximize the likelihood of observing the given MOI distribution. Furthermore, we paired our estimated FOI values for Ghana surveys with the independently measured EIR (Entomological Inoculation Rate), a common field measure of transmission intensity. We ensured that our resulting FOI-EIR points align with existing FOI-EIR pairs and the relationship between these quantities from previous studies. We acknowledge that, like model-fitting approaches, our validation for the field data is also indirect and further complicated by high variance in the relationship between EIR and FOI from previous studies.

Prompted by the reviewer’s comment, we elaborated on these points in the revised manuscript, emphasizing the indirect nature and existing constraints of our validation with field data in the Discussion section (Line 314-328). Additionally, we clarified certain basic assumptions of our agent-based model in Appendix 1-Simulation data.

(2) Another aspect of the paper is adding greater realism to the previous agent-based model, by including assumptions on missing data and under-sampling. This takes prominence in the figures and results section, but I would imagine is generally not as interesting to the less specialised reader. The apparent lack of impact of drug treatment on MOI is interesting and counterintuitive, though it is not really mentioned in the results or discussion sufficiently to allay my confusion. I would have been interested in understanding the relationship between MOI and FOI as generated by your queuing theory method and the model. It isn't clear to me why these more standard results are not presented, as I would imagine they are outputs of the model (though happy to stand corrected - it isn't entirely clear to me what the model is doing in this manuscript alone).

We thank the reviewer for this comment. Please refer to our response to Reviewer 2, comment (3), as we made changes in the revised manuscript regarding antimalarial drug treated individuals. We reported two sets of FOI estimates. In the first, we excluded these treated individuals from the analysis as suggested by Reviewer 2. In the second, we discarded their infection status and MOI estimates and sampling from non-treated individuals.

The reviewer correctly noted the surprising lack of impact of antimalarial treatment on MOI estimates. This pattern is indeed interesting and counterintuitive. The impact of the drugs likely depends on their nature, efficiency, and duration. We note that treatment information was collected via a routine questionnaire, with participant self-reporting that they had received an antimalarial treatment in the previous two-weeks before the surveys (i.e., participants that reported they were sick, sought treatment, and were provided with an antimalarial treatment). No confirmation through hospital or clinic or pharmacy records was conducted, as it was beyond the scope of the study. Additionally, many of these sick individuals seek treatment at local chemists, which may limit the relevance of hospital or clinic records, if they are even available. Consequently, information on the nature, efficiency, and duration of administrated drugs was incomplete or lacking. As this is not the focus of this work, we do not elaborate on the impact of drug treatment in the revised manuscript.

Regarding the last point of the reviewer, on understanding the relationship between MOI and FOI, we are not fully clear about what was meant. We are also confused about the statement on what the “model is doing in this manuscript alone”. We interpret the overall comment as the reviewer suggesting a better understanding of the relationship between MOI and FOI generated by the two-moment approximation method and the agent-based model. This could involve exploring the relationship between the moments of their distributions, possibly by fitting models such as simple linear regression models. Although this approach is in principle possible, it falls outside the focus of our work. Moreover, it would be challenging to evaluate the performance of this alternative approach given the lack of MOI-FOI pairs from empirical settings with directly measured FOI values (from large cohort studies). Nonetheless, we note that the qualitative relationship between the two quantities is intuitive. Higher FOI values should correspond to higher MOI values. Less variable FOI values should result in more narrow or concentrated MOI distributions, whereas more variable FOI values should lead to more spread-out MOI distributions. We described this qualitative relationship between MOI and FOI in the revised manuscript (Line 499-502).

As mentioned in the response to the reviewer’s previous point (1), we hope that our clarification of the basic assumptions underlying our agent-based model in Appendix 1-Simulation data helps the reviewer gain a better sense of the model. We appreciate agent-based models involve more assumptions and parameters than typical equation-based models in epidemiology, and their description can be difficult to follow. We have extended this description to rely less on previous publications. As for other ABMs, the population dynamics of the disease is followed over time by tracking individual hosts and strains. This allows us to implement specific immune memory to the large number of strains arising from the var multigene family. There is no equation-based formulation of the transmission dynamics that can incorporate immune memory in the presence of such large variation as well as recombination of the strains. We rely on this model because large strain diversity at high transmission underlies superinfection of individual hosts, and therefore, MOI values larger than one. We relied on the estimation of MOI with a method based on var gene sampling, and therefore, simulated such sampling for individual hosts (which requires an ABM and one that represents such genes and resulting strains explicitly).

(3) I would suggest that outside of malaria geneticists, the force of infection is considered to be the entomological inoculation rate, not the number of genetically distinct blood-stage strains. I appreciate that FOI has been used to explain the latter before by others, though the authors could avoid confusion by stating this clearly throughout the manuscript. For example, the abstract says FOI is "the number of new infections acquired by an individual host over a given time interval" which suggests the former, please consider clarifying.

We thank the reviewer for this helpful comment, as it is crucial to avoid any confusion regarding basic definitions. EIR, the entomological inoculation rate, is closely related to the FOI, force of infection, but they are not equivalent. EIR focuses on the rate of arrival of infectious bites and is measured as such by focusing on the mosquito vectors that are infectious and arrive to bite a given host. Not all these bites result in actual infection of the human host. Epidemiological models of malaria transmission clearly make this distinction, as FOI is defined as the rate at which a host acquires infection. This definition comes from more general models of the population dynamics of infectious diseases. For simpler diseases without super-infection, the typical SIR models define FOI as the rate at which a susceptible individual becomes infected. In the context of malaria, FOI refers to the number of new infections acquired by an individual host over a given time interval. This distinction between EIR and FOI is the reason why studies have investigated their relationship, with the nonlinearity of this relationship reflecting the complexity of the underlying biology and how host immunity influences the outcome of an infectious bite.

We added “blood-stage strains” to the definition of FOI in the previous manuscript, as pointed out by the reviewer, for the following reason. After an individual host acquires an infection/strain from an infectious mosquito bite, the strain undergoes a multi-stage life cycle within the host, including the liver stage and asexual blood stage. Liver-stage infections can fail to advance to the blood stage due to immunity or exceeding the blood-stage carrying capacity. Only active blood-stage infections are detectable in all direct measures of FOI. Quantities used in indirect model-fitting approaches for estimating FOI are also based on or reflect these blood-stage strains/infections. Only these blood-stage strains/infections are transmissible to other individuals, impacting disease dynamics. Ultimately, the FOI we seek to estimate is the one defined as specified above, as well as in both the previous and revised manuscripts, consistent with the epidemiological literature. We expanded on this point in the revised manuscript (Line 641-656).

(4) Line 319 says "Nevertheless, overall, our paired EIR (directly measured by the entomological team in Ghana (Tiedje et al., 2022)) and FOI values are reasonably consistent with the data points from previous studies, suggesting the robustness of our proposed methods". I would agree that the results are consistent, given that there is huge variation in Figure 4 despite the transformed scales, but I would not say this suggests a robustness of the method.

We thank the reviewer for this comment and have modified the relevant sentences to use “consistent” instead of “robust” (Line 229-231).

(5) The text is a little difficult to follow at times and sometimes requires multiple reads to understand. Greater precision is needed with the language in a few situations and some of the assumptions made in the modelling process are not referenced, making it unclear whether it is a true representation of the biology.

We thank the reviewer for this comment. As mentioned in the response to Reviewer 1 and in response to your previous points, we have shortened, reorganized and rewritten parts of the text in the revised manuscript to improve clarity and readability.

Reviewer #1 (Recommendations For The Authors):

Minor comments:

Bar graphs in Figures 6 and 7 are not an appropriate way to rigorously compare whether your estimated MOI (under different approaches) is comparable to your true MOIs. Particularly in Figure 6 it is very difficult to clearly compare what is going on. If anything in Figure 7 it looks like as MOI gets higher, Bayesian methods and barcoding are overestimating relative to the truth. The large Excel file that shows KS statistics could be better summarized (and include p-values not in a separate table) and further discussion of how these methods perform on metrics other than the mean value would be important given that MOI distributions can be heavily right skewed and these high MOI values contain a large proportion of genetic diversity which can be highly informative for the purposes of this estimation.

We appreciate the reviewer’s comment. It appears there may have been some misinterpretation of the pattern in Figure 7 in the previous manuscript. We believe the reviewer meant “as MOI gets higher, Bayesian methods and varcoding are UNDERESTIMATING relative to the truth” rather than “OVERESTIMATING”.

We agree with the reviewer that the comparison of MOI distributions can be improved. To better quantify the difference between the MOI distribution from the original varcoding method and its Bayesian formulation relative to true MOIs, we replaced the KS test conducted in the previous manuscript with two alternative, more powerful tests: the Cramer-von Mises Test and the Anderson-Darling Test. The Cramer-von Mises Test quantifies the sum of the squared differences between the two cumulative distribution functions, while the Anderson-Darling Test, a modification of the Cramer-von Mises Test, gives more weight to the tails of the distribution, as noted by the reviewer. We have summarized the results, including test statistics and their associated p-values, in a supplementary table (Line 135-149, Line 862-883, supplementary file 1-MOImethodsPerformance.xlsx and supplementary file 7-BayesianImprovement.xlsx).

Throughout the text the authors use "consistent" to describe their estimation of FOI, I know this is meant in the colloquial use of the word but consider changing this word to replicable or something similar. When talking about estimators, usually, consistency implies asymptotic convergence in probability which we do not know whether the proposed estimator does.

We thank the reviewer for this suggestion. We changed “consistent” to “replicable” in the revised manuscript.

I think there is an issue with the numbering of the figures, they are just numbered continuously between the main text and appendix between 1 and 15, but in the text, there is a different numbering system between the main text and appendix figures.

We thank the reviewer for this comment. We have double-checked to ensure that the numbering of the figures is consistent with the text in the revised manuscript. Figures are numbered continuously between the main text and the appendix. When referring to these figures in the text, we provide a prefix (i.e., Appendix 1) indicating whether the figure is in the main text or Appendix 1, followed by the figure number.

The description of the bootstrap for 95% CI is a bit sparse, did bootstrap distributions look symmetric? If not did authors use a skewness adjustment to ensure good coverage? Also, is the bootstrap unit of resampling at the individual level, the simulation scenario level, population level?

We checked the bootstrap distributions and calculated their skewness. The majority fall within the range of -0.5 to 0.5, with a few exceptions falling within the range of 0.5-0.75 (supplementary file 6-FOIBootstrapSkewness.xlsx). We considered them as fairly symmetric and thus did not use a skewness adjustment.

In Figures 8 and 9 the x-axes seem to imply there are both the true and estimated MOI distributions on the plot but only 1 color of grey is clearly visible. If there are 2 distributions the color or size needs to be changed or if not consider re-labeling the x-axis.

We thank the reviewer for this comment. There was a mistake in the x-axis labels in Figure 8 and 9. Only the estimated MOI distributions were shown because the true ones are not available for the Ghana field surveys. The labels should simply be “Estimated MOIvar”.

Reviewer #2 (Recommendations For The Authors):

(1) Throughout the results section there are lots of vague statements such as "differ only slightly", "exhibit a somewhat larger, but still small, difference", etc. Please include the exact values and ranges within the text where appropriate because it can be difficult to discern from the figure.

We thank the reviewer for this useful comment. In the revised manuscript, we have provided exact values and ranges where appropriate (supplementary file 1- MOImethodsPerformance.xlsx, supplementary file 3- FOImethodsPerformance.xlsx, and supplementary file 7-BayesianImprovement.xlsx).

(2) Truncate decimals to 2 places.

We thank the reviewer for this comment. In the revised manuscript, we have truncated decimals to two places where applicable.

(3) The queueing theory notation in the methods section is unfamiliar, specifically things like "M/M/c/k", please define the variables used.

We thank the reviewer for this useful comment. In the revised manuscript, we have defined all the variables used. Please refer to our responses to Reviewer 1 Point (1) a.

Reviewer #3 (Recommendations For The Authors):

(1) The work takes many of the models and data from a previous paper published in eLife in 2023 (the 4 most senior authors of this previous manuscript are the 4 authors of the current manuscript). This previous paper introduced some new terminology "census population" which was highlighted as being potentially confusing by 2 of the 3 reviewers of the original article. This was somewhat rebuffed by the authors, though their response was ambiguous about whether the terminology would be changed in any potential future revision. The census population terminology does not appear in this manuscript, though the same data is being used. Publication of similar papers with the same data and different terminology could generate confusion, so I would encourage authors to be consistent and make sure the two papers are in line. To this end, it feels like this paper would be better suited to be classified as a "Research Advances" on this original manuscript and linked, which is a nice functionality that eLife offers.

We thank the reviewer for this comment, but we do not think our work would fall under the criteria of “Research Advances” based on our previous paper pointed out by the reviewer. The reviewer correctly noted that the current work and the previous paper used the same datasets. However, they have different goals and are not related in terms of content.

The previous paper examined how epidemiological quantities and diversity measurements of the local parasite population change following the initiation of effective control interventions and subsequently as this control wanes. These quantities included MOI and census population size (MOI was estimated using the Bayesian formulation of the varcoding method, and the census population size was derived from summing MOIvar across individuals in the human population). In contrast, our current work focused on a different goal: inferring FOI based on MOI. We proposed two methods from queuing theory and illustrated them with MOI estimates obtained with the Bayesian formulation of the "varcoding" method. Although the method applied to estimate MOI is indeed the same as that of the paper mentioned by the reviewer, the proposed methods should be applicable to MOI estimates obtained in any other way, as stated in the Abstract in the previous manuscript. That is, the methods we present in the current paper are independent from the way the MOI estimation has been carried out. Our results are not about the MOI values themselves but rather on an illustration of the methods for converting those MOI values to FOI. In fact, there are different ways to obtain MOI estimates for Plasmodium falciparum (9). The most common approach for determining MOI involves size-polymorphic antigenic markers, such as msp1, msp2, msp3, glurp, ama1, and csp. Similarly, microsatellites, also termed simple sequence repeat (SSR), are another type of size-polymorphic marker that can be amplified to estimate MOI by determining the number of alleles detected. Combinations of genome-wide single nucleotide polymorphisms (SNPs) have also been used to estimate MOI.

The result section of the current manuscript begins by evaluating how different kinds of errors/sampling limitations affect the estimation of MOI using the Bayesian formulation of the varcoding method. Only that brief section, which is not the core or primary objective of the manuscript, could be considered an extension and an advancement related to the other paper. We considered the effect of these errors on the resulting estimates of FOI.

We further note that, as the reviewer pointed out, the census population size is not utilized at all in our current work. We are unclear on why this quantity is mentioned here. Our previous paper has been revised and can be found in eLife as such. We have not changed this terminology and have provided a clear explanation for why we chose it. The reviewer seems to have read the previous response to version 1 posted on December 28, 2023 (Note that version 2 and the associated response was posted on November 20, 2024). Regardless, this is not the place for a discussion on another paper on a quantity that is irrelevant to the current work being reviewed.

We understand that the reviewer’s impression may have been influenced by the previous emphasis on the Bayesian formulation of the varcoding method in our manuscript. With the reorganization and rewriting of parts of the manuscript, we hope the revised version will clearly convey the central goal of our work.

(2) Similar statements that could be toned down. 344 ".... two-moment approximation approach and Little's law are shown to provide consistent and good FOI estimates,.....", 374 "Thus, the flexibility and generality of these two proposed methods allow robust estimation of an important metric for malaria transmission"

We thank the reviewer for this comment. We have modified the descriptive terms for the performance of our methods. Please also refer to our responses to Reviewer 1, Point (1) c and your previous Point (1).

(3) Various assumptions seem to have been made which are not justified. For example, heterogeneous mixing is defined as 2/3rd of the population receives 90% of the bites. A reference for this would be good.

In this work, we considered heterogenous transmission arising from 2/3 of the population receiving approximately 94% of all bites, because we believe this distribution introduces a reasonable and sufficient amount of heterogeneity in exposure risk across individuals. We are not aware of field studies justifying this degree of heterogeneity.

(4) The work assumes children under 5 have no immunity (Line 648 says "It is thus safe to consider negligible the impact of immune memory accumulated from previous infections on the duration of a current infection." ). Is there supporting evidence for this and what would happen if this wasn't the case?

We thank the reviewer for this helpful comment. Please refer to our responses to Reviewer 1 Point (2) a.

(5) Similarly, there are a few instances of a need for more copy-editing. The text says "We continue with the result of the heterogeneous exposure risk scenarios in which a high-risk group ( 2/3 of the total population) receives around 94% of all bites whereas a low-risk group ( 1/3 of the total population) receives the remaining bites (Appendix 1-Figure 5C)." whereas the referenced caption says "For example, heterogeneous mixing is defined as 2/3rd of population receives 90% of the bites."

We believe there was a misinterpretation of the legend caption. In the referenced caption, we stated “2/3rd of population receives MORE THAN 90% of the bites”, which aligns with “around 94% of all bites”. Nonetheless, to maintain consistency in the revised manuscript, we have updated the description to uniformly state “approximately 94% of all bites” throughout.

(6) The term "measurement error" is used to describe the missing potential under-sampling of var genes. Given this would only go one way isn't the term "bias" more appropriate?

We understand that, in general English, “bias” might seem more precise for describing a deviation in one direction. However, in malaria epidemiology and in models for malaria and other infectious diseases, “measurement error” is a general term that describes deviations introduced in the process of measurement and sampling, which can confound or add noise to the true values being collected. This term is commonly used, and we have adhered to it in the revised manuscript.

(7) Line 739 "Though FOI and EIR both reflect transmission intensity, the former refers directly to detectable blood-stage infections whereas the latter concerns human-vector contact rates." In my mind this is not true, the EIR is the number of potentially invading parasites (a contact rate between parasites in mosquitoes and humans if you will). The human-vector contact rate is the human biting rate.

We thank the reviewer for this comment. We have clarified the definition regarding FOI and EIR in our response to your previous comment (3) and in the revised manuscript. We agree that the term “human-vector contact rates” was not precise enough for EIR. We intended “human-infectious vector contact rates”, and we have updated the text to reflect this change (Line 644-645).

References and Notes

(1) Maire, N. et al. A model for natural immunity to asexual blood stages of Plasmodium falciparum malaria in endemic areas. Am J Trop Med Hyg., 75(2 Suppl):19-31 (2006).

(2) Tiedje, K. E. et al. Measuring changes in Plasmodium falciparum census population size in response to sequential malaria control interventions. eLife, 12 (2023).

(3) Andrade C. M. et al. Infection length and host environment influence on Plasmodium falciparum dry season reservoir. EMBO Mol Med.,16(10):2349-2375 (2024).

(4) Zhang X. and Deitsch K. W. The mystery of persistent, asymptomatic Plasmodium falciparum infections, Current Opinion in Microbiology, 70:102231 (2022).

(5) Tran, T. M. et al. An Intensive Longitudinal Cohort Study of Malian Children and Adults Reveals No Evidence of Acquired Immunity to Plasmodium falciparum Infection, Clinical Infectious Diseases, 57(1):40–47 (2013).

(6) Farnert, A., Snounou, G., Rooth, I., Bjorkman, A. Daily dynamics of Plasmodium falciparum subpopulations in asymptomatic children in a holoendemic area. Am J Trop Med Hyg., 56(5):538-47 (1997).

(7) Read, A. F. and Taylor, L. H. The Ecology of Genetically Diverse Infections, Science, 292:1099-1102 (2001).

(8) Sondo, P. et al. Genetically diverse Plasmodium falciparum infections, within-host competition and symptomatic malaria in humans. Sci Rep 9(127) (2019).

(9) Labbe, F. et al. Neutral vs. non-neutral genetic footprints of Plasmodium falciparum multiclonal infections. PLoS Comput Biol, 19(1) (2023).

(10) He, Q. et al. Networks of genetic similarity reveal non-neutral processes shape strain structure in Plasmodium falciparum. Nat Commun 9(1817) (2018).