Discriminating neural ensemble patterns through dendritic computations in randomly connected feedforward networks

Reviewer #1 (Public review):

In the current manuscript, the authors use theoretical and analytical tools to examine the possibility of neural projections to engage ensembles of synaptic clusters in active dendrites. The analysis is divided into multiple models that differ in the connectivity parameters, speed of interactions and identity of the signal (electric vs. second messenger). They first show that random connectivity almost ensures the representation of presynaptic ensembles. As expected, this convergence is much more likely for small group sizes and slow processes, such as calcium dynamics. Conversely, fast signals (spikes and postsynaptic potentials) and large groups are much less likely to recruit spatially clustered inputs. Dendritic nonlinearity in the postsynaptic cells was found to play a highly important role in distinguishing these clustered activation patterns, both when activated simultaneously and in sequence. The authors tackled the difficult issue of noise, showing a beneficiary effect when noise 'happen' to fill in gaps in a sequential pattern but degraded performance at higher background activity levels. Last, the authors simulated selectivity to chemical and electrical signals. While they find that longer sequences are less perturbed by noise, in more realistic activation conditions, the signals are not well resolved in the soma.

While I think the premise of the manuscript is worth exploring, I have a number of reservations regarding the results.

(1) In the analysis, the authors made a simplifying assumption that the chemical and electrical processes are independent. However, this is not the case; excitatory inputs to spines often trigger depolarization combined with pronounced calcium influx; this mixed signaling could have dramatic implications on the analysis, particularly if the dendrites are nonlinear (see below)
(2) Sequence detection in active dendrites is often simplified to investigating activation in a part of or the entirety of individual branches. However, the authors did not do that for most of their analysis. Instead, they treat the entire dendritic tree as one long branch and count how many inputs form clusters. I fail to see why the simplification is required and suspect it can lead to wrong results. For example, two inputs that are mapped to different dendrites in the 'original' morphology but then happen to fall next to each other when the branches are staggered to form the long dendrites would be counted as neighbors.
(3) The simulations were poorly executed. Figures 5 and 6 show examples but no summary statistics. The authors emphasize the importance of nonlinear dendritic interactions, but they do not include them in their analysis of the ectopic signals! I find it to be wholly expected that the effects of dendritic ensembles are not pronounced when the dendrites are linear.

To provide a comprehensive analysis of dendritic integration, the authors could simulate more realistic synaptic conductances and voltage-gated channels. They would find much more complicated interactions between inputs on a single site, a sliding temporal and spatial window of nonlinear integration that depends on dendritic morphology, active and passive parameters and synaptic properties. At different activation levels, the rules of synaptic integration shift to cooperativity between different dendrites and cellular compartments, further complicated by nonlinear interactions between somatic spikes and dendritic events.

While it is tempting to extend back-of-the-napkin calculations of how many inputs can recruit nonlinear integration in active dendrites, the biological implementation is very different from this hypothetical. It is important to consider these questions, but I am not convinced that this manuscript adequately addressed the questions it set out to probe, nor does it provide information that was unknown beforehand.

Update after the first revision:

In this revision, the authors significantly improved the manuscript. They now address some of my concerns. Specifically, they show the contribution of end-effects on spreading the inputs between dendrites. This analysis reveals greater applicability of their findings to cortical cells, with long, unbranching dendrites than other neuronal types, such as Purkinje cells in the cerebellum.

They now explain better the interactions between calcium and voltage signals, which I believe improve the take-away message of their manuscript. They modified and added new figures that helped to provide more information about their simulations.
However, some of my points remain valid. Figure 6 shows depolarization of ~5mV from -75. This weak depolarization would not effectively recruit nonlinear activation of NMDARs. In their paper, Branco and Hausser (2010) showed depolarizations of ~10-15mV. More importantly, the signature of NMDAR activation is the prolonged plateau potential and activation at more depolarized resting membrane potentials (their Figure 4). Thus, despite including NMDARs in the simulation, the authors do not model functional recruitment of these channels. Their simulation is thus equivalent to AMPA only drive, which can indeed summate somewhat nonlinearly.

Reviewer #2 (Public review):

Summary:

If synaptic input is functionally clustered on dendrites, nonlinear integration could increase the computational power of neural networks. But this requires the right synapses to be located in the right places. This paper aims to address the question of whether such synaptic arrangements could arise by chance (i.e. without special rules for axon guidance or structural plasticity), and could therefore be exploited even in randomly connected networks. This is important, particularly for the dendrites and biological computation communities, where there is a pressing need to integrate decades of work at the single-neuron level with contemporary ideas about network function.

Using an abstract model where ensembles of neurons project randomly to a postsynaptic population, back-of-envelope calculations are presented that predict the probability of finding clustered synapses and spatiotemporal sequences. Using data-constrained parameters, the authors conclude that clustering and sequences are indeed likely to occur by chance (for large enough ensembles), but require strong dendritic nonlinearities and low background noise to be useful.

Strengths:

- The back-of-envelope reasoning presented can provide fast and valuable intuition. The authors have also made the effort to connect the model parameters with measured values. Even an approximate understanding of cluster probability can direct theory and experiments towards promising directions, or away from lost causes.

- I found the general approach to be refreshingly transparent and objective. Assumptions are stated clearly about the model and statistics of different circuits. Along with some positive results, many of the computed cluster probabilities are vanishingly small, and noise is found to be quite detrimental in several cases. This is important to know, and I was happy to see the authors take a balanced look at conditions that help/hinder clustering, rather than just focus on a particular regime that works.

- This paper is also a timely reminder that synaptic clusters and sequences can exist on multiple spatial and temporal scales. The authors present results pertaining to the standard `electrical' regime (~50-100 µm, <50 ms), as well as two modes of chemical signaling (~10 µm, 100-1000 ms). The senior author is indeed an authority on the latter, and the simulations in Figure 5, extending those from Bhalla (2017), are unique in this area. In my view, the role of chemical signaling in neural computation is understudied theoretically, but research will be increasingly important as experimental technologies continue to develop.

Weaknesses:

- The paper is mostly let down by the presentation. In the current form, some patience is needed to grasp the main questions and results, and it is hard to keep track of the many abbreviations and definitions. A paper like this can be impactful, but the writing needs to be crisp, and the logic of the derivation accessible to non-experts. See, for instance, Stepanyants, Hof & Chklovskii (2002) for a relevant example.

It would be good to see a restructure that communicates the main points clearly and concisely, perhaps leaving other observations to an optional appendix. For the interested but time-pressed reader, I recommend starting with the last paragraph of the introduction, working through the main derivation on page 7, and writing out the full expression with key parameters exposed. Next, look at Table 1 and Figure 2J to see where different circuits and mechanisms fit in this scheme. Beyond this, the sequence derivation on page 17 and biophysical simulations in Figures 5 and 6 are also highlights.

- The analysis supporting the claim that strong nonlinearities are needed for cluster/sequence detection is unconvincing. In the analysis, different synapse distributions on a single long dendrite are convolved with a sigmoid function and then the sum is taken to reflect the somatic response. In reality, dendritic nonlinearities influence the soma in a complex and dynamic manner. It may be that the abstract approach the authors use captures some of this, but it needs to be validated with simulations to be trusted (in line with previous work, e.g. Poirazi, Brannon & Mel, (2003)).

- It is unclear whether some of the conclusions would hold in the presence of learning. In the signal-to-noise analysis, all synaptic strengths are assumed equal. But if synapses involved in salient clusters or sequences were potentiated, presumably detection would become easier? Similarly, if presynaptic tuning and/or timing was reorganized through learning, the conditions for synaptic arrangements to be useful could be relaxed. Answering these questions is beyond the scope of the study, but there is a caveat there nonetheless.

Author response:

The following is the authors’ response to the original reviews.

Public Reviews:

Reviewer #1 (Public Review):

In the current manuscript, the authors use theoretical and analytical tools to examine the possibility of neural projections to engage ensembles of synaptic clusters in active dendrites. The analysis is divided into multiple models that differ in the connectivity parameters, speed of interactions, and identity of the signal (electric vs. second messenger). They first show that random connectivity almost ensures the representation of presynaptic ensembles. As expected, this convergence is much more likely for small group sizes and slow processes, such as calcium dynamics. Conversely, fast signals (spikes and postsynaptic potentials) and large groups are much less likely to recruit spatially clustered inputs. Dendritic nonlinearity in the postsynaptic cells was found to play a highly important role in distinguishing these clustered activation patterns, both when activated simultaneously and in sequence. The authors tackled the difficult issue of noise, showing a beneficiary effect when noise 'happens' to fill in gaps in a sequential pattern but degraded performance at higher background activity levels. Last, the authors simulated selectivity to chemical and electrical signals. While they find that longer sequences are less perturbed by noise, in more realistic activation conditions, the signals are not well resolved in the soma.

While I think the premise of the manuscript is worth exploring, I have a number of reservations regarding the results.

(1) In the analysis, the authors made a simplifying assumption that the chemical and electrical processes are independent. However, this is not the case; excitatory inputs to spines often trigger depolarization combined with pronounced calcium influx; this mixed signaling could have dramatic implications on the analysis, particularly if the dendrites are nonlinear (see below)

We thank the reviewer for pointing out that we were not entirely clear about the strong basis upon which we had built our analyses of nonlinearity. In the previous version we had relied on published work, notably (Bhalla 2017), which does include these nonlinearities. However, we agree it is preferable to unambiguously demonstrate all the reported selectivity properties in a single model with all the nonlinearities discussed. We have now done so. This is now reported in the paper:

“A single model exhibits multiple forms of nonlinear dendritic selectivity

We implemented all three forms of selectivity described above, in a single model which included six voltage and calcium-gated ion channels, NMDA, AMPA and GABA receptors, and chemical signaling processes in spines and dendrites. The goal of this was three fold: To show how these nonlinear operations emerge in a mechanistically detailed model, to show that they can coexist, and to show that they are separated in time-scales. We implemented a Y-branched neuron model with additional electrical compartments for the dendritic spines (Methods). This model was closely based on a published detailed chemical-electrical model (Bhalla 2017). We stimulated this model with synaptic input corresponding to the three kinds of spatiotemporal patterns described in figures Figure 8 - Supplement 1 (sequential synaptic activity triggering electrical sequence selectivity), Figure 8 - Supplement 2 (spatially grouped synaptic stimuli leading to local Ca4_CaM activation), and Figure 8 - Supplement 3 (sequential bursts of synaptic activity triggering chemical sequence selectivity). We found that each of these mechanisms show nonlinear selectivity with respect to both synaptic spacing and synaptic weights. Further, these forms of selectivity coexist in the composite model (Figure 8 Supplements 1, 2, 3), separated by the time-scales of the stimulus patterns (~ 100 ms, ~ 1s and ~10s respectively). Thus mixed signaling in active nonlinear dendrites yields selectivity of the same form as we explored in simpler individual models. A more complete analysis of the effect of morphology, branching and channel distributions deserves a separate in-depth analysis, and is outside the scope of the current study.”

(2) Sequence detection in active dendrites is often simplified to investigating activation in a part of or the entirety of individual branches. However, the authors did not do that for most of their analysis. Instead, they treat the entire dendritic tree as one long branch and count how many inputs form clusters. I fail to see why simplification is required and suspect it can lead to wrong results. For example, two inputs that are mapped to different dendrites in the 'original' morphology but then happen to fall next to each other when the branches are staggered to form the long dendrites would be counted as neighbors.

We have added the below section within the main text in the section titled “Grouped Convergence of Inputs” to address the effect of branching.

“End-effects limit convergence zones for highly branched neurons

Neurons exhibit considerable diversity with respect to their morphologies. How synapses extending across dendritic branch points interact in the context of a synaptic cluster/group, is a topic that needs detailed examination via experimental and modeling approaches. However for the sake of analysis, we present calculations under the assumption that selectivity for grouped inputs might be degraded across branch points.

Zones beginning close to a branch point might get interrupted. Consider a neuron with B branches. The length of the typical branch would be L/B. As a conservative estimate if we exclude a region of length Z for every branch, the expected number of zones that begin too close to a branch point is

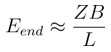[Equation 3]

For typical pyramidal neurons B~50, so Eend ~ 0.05 for values of Z of ~10 µm. Thus pyramidal neurons will not be much affected by branching effects, Profusely branching neurons like Purkinje cells have B~900 for a total L of ~7800 µm, (McConnell and Berry, 1978), hence Eend ~1 for values of Z of ~10 µm. Thus almost all groups in Purkinje neurons would run into a branch point or terminal. For the case of electrical groups, this estimate would be scaled by a factor of 5 if we consider a zone length of 50 µm. However, it is important to note that these are very conservative estimates, as for clusters of 4-5 inputs, the number of synapses available within a zone are far greater (~100 synapses within 50 µm).”

(3) The simulations were poorly executed. Figures 5 and 6 show examples but no summary statistics.

We have included the summary statistics in Figure 5F and Figure 6E. The statistics for both these panels were generated by simulating multiple spatiotemporal combinations of ectopic input in the presence of different stimulus patterns for each sequence length.

The authors emphasize the importance of nonlinear dendritic interactions, but they do not include them in their analysis of the ectopic signals! I find it to be wholly expected that the effects of dendritic ensembles are not pronounced when the dendrites are linear.

We would like to clarify that both Figures 5 and 6 already included nonlinearities. In Figure 5, the chemical mechanism involving the bistable switch motif is strongly selective for ordered inputs in a nonlinear manner. A separate panel highlighting this (Panel C) has now been included in Figure 5. This result had been previously shown in Figure 3I of (Bhalla 2017). We have reproduced it in Figure 5C.

The published electrical model used in Figure 6 also has a nonlinearity which predominantly stems from the interaction of the impedance gradient along the dendrite with the voltage dependence of NMDARs. Check Figure 4C,D of (Branco, Clark, and Häusser 2010).

To provide a comprehensive analysis of dendritic integration, the authors could simulate more realistic synaptic conductances and voltage-gated channels. They would find much more complicated interactions between inputs on a single site, a sliding temporal and spatial window of nonlinear integration that depends on dendritic morphology, active and passive parameters, and synaptic properties. At different activation levels, the rules of synaptic integration shift to cooperativity between different dendrites and cellular compartments, further complicated by nonlinear interactions between somatic spikes and dendritic events.

We would like to clarify two points. First, the key goal of our study was to understand the role played by random connectivity in giving rise to clustered computation. In this revision we provide simulations to show the mechanistic basis for the nonlinearities, and then abstracted these out in order to scale the analysis to networks. These nonlinearities were taken as a given, though we elaborated previous work slightly in order to address the question of ectopic inputs. Second, in our original submission we relied on published work for the estimates of dendritic nonlinearities. Previous work from (Poirazi, Brannon, and Mel 2003; Branco, Clark, and Häusser 2010; Bhalla 2017) have already carried out highly detailed realistic simulations, and in some cases including chemical and electrical nonlinearities as the reviewer mentions (Bhalla 2017). Hence we did not feel that this needed to be redone.

In this resubmission we have addressed the above and two additional concerns, namely whether the different forms of selectivity can coexist in a single model including all these nonlinearities, and whether there is separation of time-scales. The answer is yes to both. The outcome of this is presented in Figure 8 and the associated supplementary figures, and all simulation details are provided on the github repository associated with this paper. A more complete analysis of interaction of multiple nonlinearities in a detailed model is material for further study.

While it is tempting to extend back-of-the-napkin calculations of how many inputs can recruit nonlinear integration in active dendrites, the biological implementation is very different from this hypothetical. It is important to consider these questions, but I am not convinced that this manuscript adequately addressed the questions it set out to probe, nor does it provide information that was unknown beforehand.

We developed our analysis systematically, and perhaps the reviewer refers to the first few calculations as back-of-the-napkin. However, the derivation rapidly becomes more complex when we factor in combinatorics and the effect of noise. This derivation is in the supplementary material. Furthermore, the exact form of the combinatorial and noise equations was non-trivial to derive and we worked closely with the connectivity simulations (Figures 2 and 4) to obtain equations which scale across a large parameter space by sampling connectivity for over 100000 neurons and activity over 100 trials for each of these neurons for each network configuration we have tested.

the biological implementation is very different from this hypothetical.

We do not quite understand in what respect the reviewer feels that this calculation is very different from the biological implementation. The calculation is about projection patterns. In the discussion we consider at length how our findings of selectivity from random projections may be an effective starting point for more elaborate biological connection rules. We have added the following sentence:

“We present a first-order analysis of the simplest kind of connectivity rule (random), upon which more elaborate rules such as spatial gradients and activity-dependent wiring may be developed.”

In case the reviewer was referring to the biological implementation of nonlinear integration, we treat the nonlinear integration in the dendrites as a separate set of simulations, most of which are closely based on published work (Bhalla 2017). We use these in the later sections of the paper to estimate selectivity terms, which inform our final analysis.

In the revision we have worked to clarify this progression of the analysis. As indicated above, we have also made a composite model of all of the nonlinear dendritic mechanisms, chemical and electrical, which underlie our analysis.

nor does it provide information that was unknown beforehand.

We conducted a broad literature survey and to the best of our knowledge these calculations and findings have not been obtained previously. If the reviewer has some specific examples in mind we would be pleased to refer to it.

Reviewer #2 (Public Review):

Summary:

If synaptic input is functionally clustered on dendrites, nonlinear integration could increase the computational power of neural networks. But this requires the right synapses to be located in the right places. This paper aims to address the question of whether such synaptic arrangements could arise by chance (i.e. without special rules for axon guidance or structural plasticity), and could therefore be exploited even in randomly connected networks. This is important, particularly for the dendrites and biological computation communities, where there is a pressing need to integrate decades of work at the single-neuron level with contemporary ideas about network function.

Using an abstract model where ensembles of neurons project randomly to a postsynaptic population, back-of-envelope calculations are presented that predict the probability of finding clustered synapses and spatiotemporal sequences. Using data-constrained parameters, the authors conclude that clustering and sequences are indeed likely to occur by chance (for large enough ensembles), but require strong dendritic nonlinearities and low background noise to be useful.

Strengths:

(1) The back-of-envelope reasoning presented can provide fast and valuable intuition. The authors have also made the effort to connect the model parameters with measured values. Even an approximate understanding of cluster probability can direct theory and experiments towards promising directions, or away from lost causes.

(2) I found the general approach to be refreshingly transparent and objective. Assumptions are stated clearly about the model and statistics of different circuits. Along with some positive results, many of the computed cluster probabilities are vanishingly small, and noise is found to be quite detrimental in several cases. This is important to know, and I was happy to see the authors take a balanced look at conditions that help/hinder clustering, rather than to just focus on a particular regime that works.

(3) This paper is also a timely reminder that synaptic clusters and sequences can exist on multiple spatial and temporal scales. The authors present results pertaining to the standard `electrical' regime (~50-100 µm, <50 ms), as well as two modes of chemical signaling (~10 µm, 100-1000 ms). The senior author is indeed an authority on the latter, and the simulations in Figure 5, extending those from Bhalla (2017), are unique in this area. In my view, the role of chemical signaling in neural computation is understudied theoretically, but research will be increasingly important as experimental technologies continue to develop.

Weaknesses:

(1) The paper is mostly let down by the presentation. In the current form, some patience is needed to grasp the main questions and results, and it is hard to keep track of the many abbreviations and definitions. A paper like this can be impactful, but the writing needs to be crisp, and the logic of the derivation accessible to non-experts. See, for instance, Stepanyants, Hof & Chklovskii (2002) for a relevant example.

It would be good to see a restructure that communicates the main points clearly and concisely, perhaps leaving other observations to an optional appendix. For the interested but time-pressed reader, I recommend starting with the last paragraph of the introduction, working through the main derivation on page 7, and writing out the full expression with key parameters exposed. Next, look at Table 1 and Figure 2J to see where different circuits and mechanisms fit in this scheme. Beyond this, the sequence derivation on page 15 and biophysical simulations in Figures 5 and 6 are also highlights.

We appreciate the reviewers' suggestions. We have tightened the flow of the introduction. We understand that the abbreviations and definitions are challenging and have therefore provided intuitions and summaries of the equations discussed in the main text.

Clusters calculations

“Our approach is to ask how likely it is that a given set of inputs lands on a short segment of dendrite, and then scale it up to all segments on the entire dendritic length of the cell.

Thus, the probability of occurrence of groups that receive connections from each of the M ensembles (PcFMG) is a function of the connection probability (p) between the two layers, the number of neurons in an ensemble (N), the relative zone-length with respect to the total dendritic arbor (Z/L) and the number of ensembles (M).”

Sequence calculations

“Here we estimate the likelihood of the first ensemble input arriving anywhere on the dendrite, and ask how likely it is that succeeding inputs of the sequence would arrive within a set spacing.

Thus, the probability of occurrence of sequences that receive sequential connections (PcPOSS) from each of the M ensembles is a function of the connection probability (p) between the two layers, the number of neurons in an ensemble (N), the relative window size with respect to the total dendritic arbor (Δ/L) and the number of ensembles (M).”

(2) I wonder if the authors are being overly conservative at times. The result highlighted in the abstract is that 10/100000 postsynaptic neurons are expected to exhibit synaptic clustering. This seems like a very small number, especially if circuits are to rely on such a mechanism. However, this figure assumes the convergence of 3-5 distinct ensembles. Convergence of inputs from just 2 ense mbles would be much more prevalent, but still advantageous computationally. There has been excitement in the field about experiments showing the clustering of synapses encoding even a single feature.

We agree that short clusters of two inputs would be far more likely. We focused our analysis on clusters with three of more ensembles because of the following reasons:

(1) The signal to noise in these clusters was very poor as the likelihood of noise clusters is high.

(2) It is difficult to trigger nonlinearities with very few synaptic inputs.

(3) At the ensemble sizes we considered (100 for clusters, 1000 for sequences), clusters arising from just two ensembles would result in high probability of occurrence on all neurons in a network (~50% in cortex, see p_CMFG in figures below.). These dense neural representations make it difficult for downstream networks to decode (Foldiak 2003).

However, in the presence of ensembles containing fewer neurons or when the connection probability between the layers is low, short clusters can result in sparse representations (Figure 2 - Supplement 2). Arguments 1 and 2 hold for short sequences as well.

(3) The analysis supporting the claim that strong nonlinearities are needed for cluster/sequence detection is unconvincing. In the analysis, different synapse distributions on a single long dendrite are convolved with a sigmoid function and then the sum is taken to reflect the somatic response. In reality, dendritic nonlinearities influence the soma in a complex and dynamic manner. It may be that the abstract approach the authors use captures some of this, but it needs to be validated with simulations to be trusted (in line with previous work, e.g. Poirazi, Brannon & Mel, (2003)).

We agree that multiple factors might affect the influence of nonlinearities on the soma. The key goal of our study was to understand the role played by random connectivity in giving rise to clustered computation. Since simulating a wide range of connectivity and activity patterns in a detailed biophysical model was computationally expensive, we analyzed the exemplar detailed models for nonlinearity separately (Figures 5, 6, and new figure 8), and then used our abstract models as a proxy for understanding population dynamics. A complete analysis of the role played by morphology, channel kinetics and the effect of branching requires an in-depth study of its own, and some of these questions have already been tackled by (Poirazi, Brannon, and Mel 2003; Branco, Clark, and Häusser 2010; Bhalla 2017). However, in the revision, we have implemented a single model which incorporates the range of ion-channel, synaptic and biochemical signaling nonlinearities which we discuss in the paper (Figure 8, and Figure 8 Supplement 1, 2,3). We use this to demonstrate all three forms of sequence and grouped computation we use in the study, where the only difference is in the stimulus pattern and the separation of time-scales inherent in the stimuli.

(4) It is unclear whether some of the conclusions would hold in the presence of learning. In the signal-to-noise analysis, all synaptic strengths are assumed equal. But if synapses involved in salient clusters or sequences were potentiated, presumably detection would become easier? Similarly, if presynaptic tuning and/or timing were reorganized through learning, the conditions for synaptic arrangements to be useful could be relaxed. Answering these questions is beyond the scope of the study, but there is a caveat there nonetheless.

We agree with the reviewer. If synapses receiving connectivity from ensembles had stronger weights, this would make detection easier. Dendritic spikes arising from clustered inputs have been implicated in local cooperative plasticity (Golding, Staff, and Spruston 2002; Losonczy, Makara, and Magee 2008). Further, plasticity related proteins synthesized at a synapse undergoing L-LTP can diffuse to neighboring weakly co-active synapses, and thereby mediate cooperative plasticity (Harvey et al. 2008; Govindarajan, Kelleher, and Tonegawa 2006; Govindarajan et al. 2011). Thus if clusters of synapses were likely to be co-active, they could further engage these local plasticity mechanisms which could potentiate them while not potentiating synapses that are activated by background activity. This would depend on the activity correlation between synapses receiving ensemble inputs within a cluster vs those activated by background activity. We have mentioned some of these ideas in a published opinion paper (Pulikkottil, Somashekar, and Bhalla 2021). In the current study, we wanted to understand whether even in the absence of specialized connection rules, interesting computations could still emerge. Thus, we focused on asking whether clustered or sequential convergence could arise even in a purely randomly connected network, with the most basic set of assumptions. We agree that an analysis of how selectivity evolves with learning would be an interesting topic for further work.

References

Bhalla, Upinder S. 2017. “Synaptic Input Sequence Discrimination on Behavioral Timescales Mediated by Reaction-Diffusion Chemistry in Dendrites.” Edited by Frances K Skinner. eLife 6 (April):e25827. https://doi.org/10.7554/eLife.25827.

Branco, Tiago, Beverley A. Clark, and Michael Häusser. 2010. “Dendritic Discrimination of Temporal Input Sequences in Cortical Neurons.” Science (New York, N.Y.) 329 (5999): 1671–75. https://doi.org/10.1126/science.1189664.

Foldiak, Peter. 2003. “Sparse Coding in the Primate Cortex.” The Handbook of Brain Theory and Neural Networks. https://research-repository.st-andrews.ac.uk/bitstream/handle/10023/2994/FoldiakSparse HBTNN2e02.pdf?sequence=1.

Golding, Nace L., Nathan P. Staff, and Nelson Spruston. 2002. “Dendritic Spikes as a Mechanism for Cooperative Long-Term Potentiation.” Nature 418 (6895): 326–31. https://doi.org/10.1038/nature00854.

Govindarajan, Arvind, Inbal Israely, Shu-Ying Huang, and Susumu Tonegawa. 2011. “The Dendritic Branch Is the Preferred Integrative Unit for Protein Synthesis-Dependent LTP.” Neuron 69 (1): 132–46. https://doi.org/10.1016/j.neuron.2010.12.008.

Govindarajan, Arvind, Raymond J. Kelleher, and Susumu Tonegawa. 2006. “A Clustered Plasticity Model of Long-Term Memory Engrams.” Nature Reviews Neuroscience 7 (7): 575–83. https://doi.org/10.1038/nrn1937.

Harvey, Christopher D., Ryohei Yasuda, Haining Zhong, and Karel Svoboda. 2008. “The Spread of Ras Activity Triggered by Activation of a Single Dendritic Spine.” Science (New York, N.Y.) 321 (5885): 136–40. https://doi.org/10.1126/science.1159675.

Losonczy, Attila, Judit K. Makara, and Jeffrey C. Magee. 2008. “Compartmentalized Dendritic Plasticity and Input Feature Storage in Neurons.” Nature 452 (7186): 436–41. https://doi.org/10.1038/nature06725.

Poirazi, Panayiota, Terrence Brannon, and Bartlett W. Mel. 2003. “Pyramidal Neuron as Two-Layer Neural Network.” Neuron 37 (6): 989–99. https://doi.org/10.1016/S0896-6273(03)00149-1.

Pulikkottil, Vinu Varghese, Bhanu Priya Somashekar, and Upinder S. Bhalla. 2021.

“Computation, Wiring, and Plasticity in Synaptic Clusters.” Current Opinion in Neurobiology, Computational Neuroscience, 70 (October):101–12. https://doi.org/10.1016/j.conb.2021.08.001.