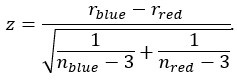Detecting Regime Shifts: Neurocomputational Substrates for Over- and Underreactions to Change

Reviewer #1 (Public review):

Summary:

The study examines human biases in a regime-change task, in which participants have to report the probability of a regime change in the face of noisy data. The behavioral results indicate that humans display systematic biases, in particular, overreaction in stable but noisy environments and underreaction in volatile settings with more certain signals. fMRI results suggest that a frontoparietal brain network is selectively involved in representing subjective sensitivity to noise, while the vmPFC selectively represents sensitivity to the rate of change.

Strengths:

(1) The study relies on a task that measures regime-change detection primarily based on descriptive information about the noisiness and rate of change. This distinguishes the study from prior work using reversal-learning or change-point tasks in which participants are required to learn these parameters from experiences. The authors discuss these differences comprehensively.

(2) The study uses a simple Bayes-optimal model combined with model fitting, which seems to describe the data well.

(3) The authors apply model-based fMRI analyses that provide a close link to behavioral results, offering an elegant way to examine individual biases.

Weaknesses:

My major concern is about the correlational analysis in the section "Under- and overreactions are associated with selectivity and sensitivity of neural responses to system parameters", shown in Figures 5c and d (and similarly in Figure 6). The authors argue that a frontoparietal network selectively represents sensitivity to signal diagnosticity, while the vmPFC selectively represents transition probabilities. This claim is based on separate correlational analyses for red and blue across different brain areas. The authors interpret the finding of a significant correlation in one case (blue) and an insignificant correlation (red) as evidence of a difference in correlations (between blue and red) but don't test this directly. This has been referred to as the "interaction fallacy" (Niewenhuis et al., 2011; Makin & Orban de Xivry 2019). Not directly testing the difference in correlations (but only the differences to zero for each case) can lead to wrong conclusions. For example, in Figure 5c, the correlation for red is r = 0.32 (not significantly different from zero) and r = 0.48 (different from zero). However, the difference between the two is 0.1, and it is likely that this difference itself is not significant. From a statistical perspective, this corresponds to an interaction effect that has to be tested directly. It is my understanding that analyses in Figure 6 follow the same approach.

Relevant literature on this point is:

Nieuwenhuis, S, Forstmann, B & Wagenmakers, EJ (2011). Erroneous analyses of interactions in neuroscience: a problem of significance. Nat Neurosci 14, 1105-1107. https://doi.org/10.1038/nn.2886

Makin TR, Orban de Xivry, JJ (2019). Science Forum: Ten common statistical mistakes to watch out for when writing or reviewing a manuscript. eLife 8:e48175. https://doi.org/10.7554/eLife.48175

There is also a blog post on simulation-based comparisons, which the authors could check out: https://garstats.wordpress.com/2017/03/01/comp2dcorr/

I recommend that the authors carefully consider what approach works best for their purposes. It is sometimes recommended to directly compare correlations based on Monte-Carlo simulations (cf Makin & Orban). It might also be appropriate to run a regression with the dependent variable brain activity (Y) and predictors brain area (X) and the model-based term of interest (Z). In this case, they could include an interaction term in the model:

Y = \beta_0 + \beta_1 \cdot X + \beta_2 \cdot Z + \beta_3 \cdot X \cdot Z

The interaction term reflects if the relationship between the model term Z and brain activity Y is conditional on the brain area of interest X.

Another potential concern is that some important details about the parameter estimation for the system-neglect model are missing. In the respective section in the methods, the authors mention a nonlinear regression using Matlab's "fitnlm" function, but it remains unclear how the model was parameterized exactly. In particular, what are the properties of this nonlinear function, and what are the assumptions about the subject's motor noise? I could imagine that by using the inbuild function, the assumption was that residuals are Gaussian and homoscedastic, but it is possible that the assumption of homoscedasticity is violated, and residuals are systematically larger around p=0.5 compared to p=0 and p=1.

Relatedly, in the parameter recovery analyses, the authors assume different levels of motor noise. Are these values representative of empirical values?

The main study is based on N=30 subjects, as are the two control studies. Since this work is about individual differences (in particular w.r.t. to neural representations of noise and transition probabilities in the frontoparietal network and the vmPFC), I'm wondering how robust the results are. Is it likely that the results would replicate with a larger number of subjects? Can the two control studies be leveraged to address this concern to some extent?

It seems that the authors have not counterbalanced the colors and that subjects always reported the probability of the blue regime. If so, I'm wondering why this was not counterbalanced.

Reviewer #2 (Public review):

Summary:

This paper focuses on understanding the behavioral and neural basis of regime shift detection, a common yet hard problem that people encounter in an uncertain world. Using a regime-shift task, the authors examined cognitive factors influencing belief updates by manipulating signal diagnosticity and environmental volatility. Behaviorally, they have found that people demonstrate both over and under-reaction to changes given different combinations of task parameters, which can be explained by a unified system-neglect account. Neurally, the authors have found that the vmPFC-striatum network represents current belief as well as belief revision unique to the regime detection task. Meanwhile, the frontoparietal network represents cognitive factors influencing regime detection i.e., the strength of the evidence in support of the regime shift and the intertemporal belief probability. The authors further link behavioral signatures of system neglect with neural signals and have found dissociable patterns, with the frontoparietal network representing sensitivity to signal diagnosticity when the observation is consistent with regime shift and vmPFC representing environmental volatility, respectively. Together, these results shed light on the neural basis of regime shift detection especially the neural correlates of bias in belief update that can be observed behaviorally.

Strengths:

(1) The regime-shift detection task offers a solid ground to examine regime-shift detection without the potential confounding impact of learning and reward. Relatedly, the system-neglect modeling framework provides a unified account for both over or under-reacting to environmental changes, allowing researchers to extract a single parameter reflecting people's sensitivity to changes in decision variables and making it desirable for neuroimaging analysis to locate corresponding neural signals.

(2) The analysis for locating brain regions related to belief revision is solid. Within the current task, the authors look for brain regions whose activation covary with both current belief and belief change. Furthermore, the authors have ruled out the possibility of representing mere current belief or motor signal by comparing the current study results with two other studies. This set of analyses is very convincing.

(3) The section on using neuroimaging findings (i.e., the frontoparietal network is sensitive to evidence that signals regime shift) to reveal nuances in behavioral data (i.e., belief revision is more sensitive to evidence consistent with change) is very intriguing. I like how the authors structure the flow of the results, offering this as an extra piece of behavioral findings instead of ad-hoc implanting that into the computational modeling.

Weaknesses:

(1) The authors have presented two sets of neuroimaging results, and it is unclear to me how to reason between these two sets of results, especially for the frontoparietal network. On one hand, the frontoparietal network represents belief revision but not variables influencing belief revision (i.e., signal diagnosticity and environmental volatility). On the other hand, when it comes to understanding individual differences in regime detection, the frontoparietal network is associated with sensitivity to change and consistent evidence strength. I understand that belief revision correlates with sensitivity to signals, but it can probably benefit from formally discussing and connecting these two sets of results in discussion. Relatedly, the whole section on behavioral vs. neural slope results was not sufficiently discussed and connected to the existing literature in the discussion section. For example, the authors could provide more context to reason through the finding that striatum (but not vmPFC) is not sensitive to volatility.

(2) More details are needed for behavioral modeling under the system-neglect framework, particularly results on model comparison. I understand that this model has been validated in previous publications, but it is unclear to me whether it provides a superior model fit in the current dataset compared to other models (e.g., a model without \alpha or \beta). Relatedly, I wonder whether the final result section can be incorporated into modeling as well - i.e., the authors could test a variant of the model with two \betas depending on whether the observation is consistent with a regime shift and conduct model comparison.

Author response:

eLife Assessment

This study provides valuable insights into the behavioral, computational, and neural mechanisms of regime shift detection, by identifying distinct roles for the frontoparietal network and ventromedial prefrontal cortex in sensitivity to signal diagnosticity and transition probabilities, respectively. The findings are supported by solid evidence, including an innovative task design, robust behavioral modeling, and well-executed model-based fMRI analyses, though claims of neural selectivity would benefit from more rigorous statistical comparisons. Overall, this work advances our understanding of how humans adapt belief updating in dynamic environments and offers a framework for exploring biases in decision-making under uncertainty.

Thank you for reviewing our manuscript. We appreciate the editors’ assessment and the reviewers’ constructive comments. Below we address the reviewers’ comments. In particular, we addressed Reviewer 1’s comments on (1) neural selectivity by performing statistical comparisons and (2) parameter estimation by providing more details on how the system-neglect model was parameterized. We addressed Reviewer 2’s comments on (1) our neuroimaging results regarding frontoparietal network and (2) model comparisons.

Public Reviews:

Reviewer #1 (Public review):

Summary:

The study examines human biases in a regime-change task, in which participants have to report the probability of a regime change in the face of noisy data. The behavioral results indicate that humans display systematic biases, in particular, overreaction in stable but noisy environments and underreaction in volatile settings with more certain signals. fMRI results suggest that a frontoparietal brain network is selectively involved in representing subjective sensitivity to noise, while the vmPFC selectively represents sensitivity to the rate of change.

Strengths:

(1) The study relies on a task that measures regime-change detection primarily based on descriptive information about the noisiness and rate of change. This distinguishes the study from prior work using reversal-learning or change-point tasks in which participants are required to learn these parameters from experiences. The authors discuss these differences comprehensively.

Thank you for recognizing our contribution to the regime-change detection literature and our effort in discussing our findings in relation to the experience-based paradigms.

(2) The study uses a simple Bayes-optimal model combined with model fitting, which seems to describe the data well.

Thank you for recognizing the contribution of our Bayesian framework and system-neglect model.

(3) The authors apply model-based fMRI analyses that provide a close link to behavioral results, offering an elegant way to examine individual biases.

Thank you for recognizing our execution of model-based fMRI analyses and effort in using those analyses to link with behavioral biases.

Weaknesses:

My major concern is about the correlational analysis in the section "Under- and overreactions are associated with selectivity and sensitivity of neural responses to system parameters", shown in Figures 5c and d (and similarly in Figure 6). The authors argue that a frontoparietal network selectively represents sensitivity to signal diagnosticity, while the vmPFC selectively represents transition probabilities. This claim is based on separate correlational analyses for red and blue across different brain areas. The authors interpret the finding of a significant correlation in one case (blue) and an insignificant correlation (red) as evidence of a difference in correlations (between blue and red) but don't test this directly. This has been referred to as the "interaction fallacy" (Niewenhuis et al., 2011; Makin & Orban de Xivry 2019). Not directly testing the difference in correlations (but only the differences to zero for each case) can lead to wrong conclusions. For example, in Figure 5c, the correlation for red is r = 0.32 (not significantly different from zero) and r = 0.48 (different from zero). However, the difference between the two is 0.1, and it is likely that this difference itself is not significant. From a statistical perspective, this corresponds to an interaction effect that has to be tested directly. It is my understanding that analyses in Figure 6 follow the same approach.

Relevant literature on this point is:

Nieuwenhuis, S, Forstmann, B & Wagenmakers, EJ (2011). Erroneous analyses of interactions in neuroscience: a problem of significance. Nat Neurosci 14, 1105-1107. https://doi.org/10.1038/nn.2886

Makin TR, Orban de Xivry, JJ (2019). Science Forum: Ten common statistical mistakes to watch out for when writing or reviewing a manuscript. eLife 8:e48175. https://doi.org/10.7554/eLife.48175

There is also a blog post on simulation-based comparisons, which the authors could check out: https://garstats.wordpress.com/2017/03/01/comp2dcorr/

I recommend that the authors carefully consider what approach works best for their purposes. It is sometimes recommended to directly compare correlations based on Monte-Carlo simulations (cf Makin & Orban). It might also be appropriate to run a regression with the dependent variable brain activity (Y) and predictors brain area (X) and the model-based term of interest (Z). In this case, they could include an interaction term in the model:

Y = \beta_0 + \beta_1 \cdot X + \beta_2 \cdot Z + \beta_3 \cdot X \cdot Z

The interaction term reflects if the relationship between the model term Z and brain activity Y is conditional on the brain area of interest X.

Thank you for this great suggestion. We tested the difference in correlation both parametrically and nonparametrically. Their results were identical. In our parametric test, we used the Fisher z transformation to transform the difference in correlation coefficients to the z statistic (Fisher, 1921). That is, for two correlation coefficients, r_blue (the correlation between behavioral slope, and neural slope estimated at change-consistent signals; sample size n_blue) and r_red, (the correlation between behavioral slope, and neural slope estimated at change-consistent signals; sample size n_red), the z statistic of the difference in correlation is given by

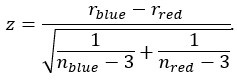
We found that among the five ROIs in the frontoparietal network, two of them, namely the left IFG and left IPS, the difference in correlation was significant (one-tailed z test; left IFG: z=1.8355, p=0.0332; left IPS: z=2.3782, p=0.0087). For the remaining three ROIs, the difference in correlation was not significant (dmPFC: z=0.7594, p=0.2238 ; right IFG: z=0.9068, p=0.1822; right IPS: z=1.3764, p=0.0843). We chose one-tailed test because we already know the correlation under the blue signals was significantly greater than 0. Hence the alternative hypothesis is that r_blue–r_red>0.

In our nonparametric test, we performed nonparametric bootstrapping to test for the difference in correlation. That is, we resampled with replacement the dataset (subject-wise) and used the resampled dataset to compute the difference in correlation. We then repeated the above for 100,000 times so as to obtain the distribution of the correlation difference. We then tested for significance and estimated p-value based on this distribution. Consistent with our parametric tests, here we also found that the difference in correlation was significant in left IFG and left IPS (left IFG: r_blue–r_red=0.46, p=0.0496; left IPS: r_blue–r_red=0.5306, p=0.0041), but was not significant in dmPFC, right IFG, and right IPS (dmPFC: r_blue–r_red=0.1634, p=0.1919; right IFG: r_blue–r_red=0.2123, p=0.1681; right IPS: r_blue–r_red=0.3434, p=0.0631).

We will update these results in the revised manuscript. In summary, we found that the left IFG and left IPS in the frontoparietal network differentially responded to signals consistent with change (blue signals) compared with signals inconsistent with change (red signals). First, the neural sensitivity to signal diagnosticity measured when signals consistent with change appeared (blue signals) significantly correlated with individual subjects’ behavioral sensitivity to signal diagnosticity (r_blue). By contrast, neural sensitivity to signal diagnosticity measured when signals inconsistent with change appeared did not significantly correlate with behavioral sensitivity (r_red). Second, the difference in correlation, r_blue–r_red, was statistically significant between correlation obtained at signals consistent with change and correlation obtained at signals inconsistent with change.

Another potential concern is that some important details about the parameter estimation for the system-neglect model are missing. In the respective section in the methods, the authors mention a nonlinear regression using Matlab's "fitnlm" function, but it remains unclear how the model was parameterized exactly. In particular, what are the properties of this nonlinear function, and what are the assumptions about the subject's motor noise? I could imagine that by using the inbuild function, the assumption was that residuals are Gaussian and homoscedastic, but it is possible that the assumption of homoscedasticity is violated, and residuals are systematically larger around p=0.5 compared to p=0 and p=1. Relatedly, in the parameter recovery analyses, the authors assume different levels of motor noise. Are these values representative of empirical values?

We thank the reviewer for this excellent point. The reviewer touched on model parameterization, assumption of noise, and parameter recovery analysis, which we answered below.

On our model was parameterized

We parameterized the model according to the system-neglect model in Eq. (2) and estimated the alpha parameter separately for each level of transition probability and the beta parameter separately for each level of signal diagnosticity. As a result, we had a total of 6 parameters (3 alpha and 3 beta parameters) in the model. The system-neglect model is then called by fitnlm so that these parameters can be estimated. The term ‘nonlinear’ regression in fitnlm refers to the fact that you can specify any model (in our case the system-neglect model) and estimate its parameters when calling this function. In our use of fitnlm, we assume that the noise is Gaussian and homoscedastic (the default option).

On the assumptions about subject’s motor noise

We wish to emphasize that we did not call the noise ‘motor’ because it can be estimation noise as well. Regardless, in the context of fitnlm, we assume that the noise is Gaussian and homoscedastic.

On the possibility that homoscedasticity is violated

In the revision, we plan to examine this possibility (residuals larger around p=0.5 compared with p=0 and p=1).

On whether the noise levels in parameter recovery analysis are representative of empirical values

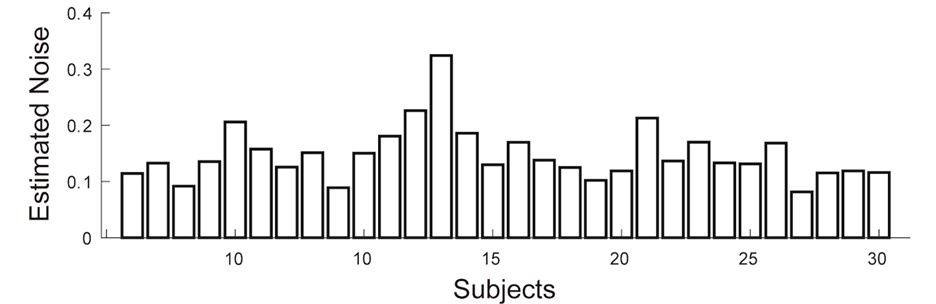
To address the reviewer’s question, we conducted a new analysis using maximum likelihood estimation to estimate the noise level of each individual subject. We proceeded in the following steps. First, for each subject separately, we used the parameter estimates of the system-neglect model to compute the period-wise probability estimates of regime shift. As a reminder, we referred to a ‘period’ as the time when a new signal appeared during a trial (for a given transition probability and signal diagnosticity). Each trial consisted of 10 successive periods. Second, we computed the period-wise likelihood, the probability of observing the subject’s actual probability estimate given the probability estimate predicted by the system-neglect model and the noise level. Here we define noise as the standard deviation of a Gaussian distribution centered at the model-predicted probability estimate. We then summed over all periods the negative logarithm of likelihood and used MATLAB’s minimization algorithm (the ‘fmincon’ function) to obtain the noise estimate that minimized the sum of negative log likelihood (thus the noise estimate that maximized the sum of log likelihood). Across subjects, we found that the mean noise estimate was 0.1480 and ranged from 0.0816 to 0.3239. The noise estimate of each subject can be seen in the figure below.

Author response image 1.

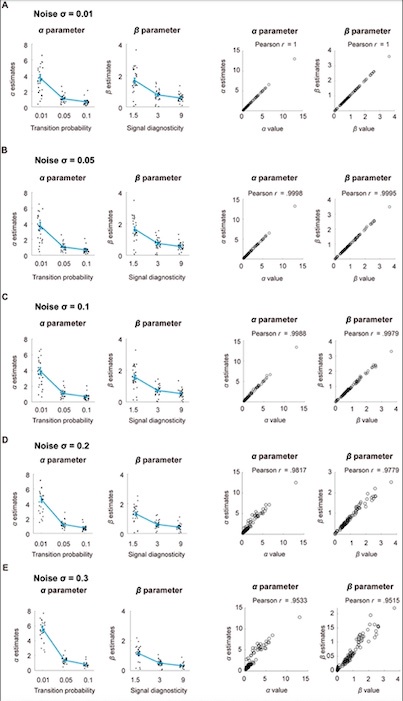
Compared with our original parameter recovery analysis where the maximum noise level was set at 0.1, our data indicated that some subjects’ noise was larger than this value. Therefore, we expanded our parameter recovery analysis to include noise levels beyond 0.1 to up to 0.3. We found good parameter recovery across different levels of noise, with the Pearson correlation coefficient between the input parameter values used to simulate data and the estimated parameter values greater 0.95 (Supplementary Fig. S3). The results will be updated in Supplementary Fig. S3.

We will update the parameter recovery section (p. 44) and Supplementary Figure S3 to incorporate these new results:

“We implemented 5 levels of noise with σ={0.01,0.05,0.1,0.2,0.3} and examined the impact of noise on parameter recovery for each level of noise. These noise levels covered the range of empirical noise levels we estimated from the subjects. To estimate each subject’s noise level, we carried out maximum likelihood estimation in the following steps. First, for each subject separately, we used the parameter estimates of the system-neglect model to compute the period-wise probability estimates of regime shift. As a reminder, we referred to a ‘period’ as the time when a new signal appeared during a trial (for a given transition probability and signal diagnosticity). Each trial consisted of 10 successive periods. Second, we computed the period-wise likelihood, the probability of observing the subject’s actual probability estimate given the probability estimate predicted by the system-neglect model and the noise level. Here we define noise as the standard deviation of a Gaussian distribution centered at the model-predicted probability estimate. We then summed over all periods the negative natural logarithm of likelihood and used MATLAB’s minimization algorithm (the ‘fmincon’ function) to obtain the noise estimate that minimized the sum of negative log likelihood (thus the noise estimate that maximized the sum of log likelihood). Across subjects, we found that the mean noise estimate was 0.1480 and ranged from 0.0816 to 0.3239 (Supplementary Figure S3).”

The main study is based on N=30 subjects, as are the two control studies. Since this work is about individual differences (in particular w.r.t. to neural representations of noise and transition probabilities in the frontoparietal network and the vmPFC), I'm wondering how robust the results are. Is it likely that the results would replicate with a larger number of subjects? Can the two control studies be leveraged to address this concern to some extent?

It would be challenging to use the control studies to address the robustness concern. The control studies were designed to address the motor confounds. They were less suitable, however, for addressing the individual difference issue raised by the reviewer. We discussed why this is the case below.

The two control studies did not allow us to examine individual differences – in particular with respect to neural selectivity of noise and transition probability – and therefore we think it is less likely to leverage the control studies. Having said that, it is possible to look at neural selectivity of noise (signal diagnosticity) in the first control experiment where subjects estimated the probability of blue regime in a task where there was no regime change (transition probability was 0). However, the fact that there were no regime shifts in the first control experiment changed the nature of the task. Instead of always starting at the Red regime in the main experiment, in the first control experiment we randomly picked the regime to draw the signals from. It also changed the meaning and the dynamics of the signals (red and blue) that would appear. In the main experiment the blue signal is a signal consistent with change, but in the control experiment this is no longer the case. In the main experiment, the frequency of blue signals is contingent upon both noise and transition probability where blue signals are less frequent than red signals because of the small transition probabilities. But in the first control experiment, the frequency of blue signals is not less frequent because the regime was blue in half of the trials. Due to these differences, we do not see how analyzing the control experiments could help in establishing robustness because we do not have a good prediction as to whether and how the neural selectivity would be impacted by these differences.

We can address the issue of robustness through looking at the effect size. In particular, with respect to individual differences in neural sensitivity of transition probability and signal diagnosticity, since the significant correlation coefficients between neural and behavioral sensitivity were between 0.4 and 0.58 for signal diagnosticity in frontoparietal network (Fig. 5C), and -0.38 and -0.37 for transition probability in vmPFC (Fig. 5D), the effect size of these correlation coefficients was considered medium to large (Cohen, 1992). Cohen, J. (1992). A power primer. Psychological Bulletin, 112(1), 155-159.

It seems that the authors have not counterbalanced the colors and that subjects always reported the probability of the blue regime. If so, I'm wondering why this was not counterbalanced.

We are aware of the reviewer’s concern. The first reason we did not do these (color counterbalancing and report blue/red regime balancing) was to not confuse the subjects in an already complicated task. Balancing these two variables also comes at the cost of sample size, which was the second reason we did not do it. Although we can elect to do these balancing at the between-subject level to not impact the task complexity, we could have introduced another confound that is the individual differences in how people respond to these variables. This is the third reason we were hesitant to do these counterbalancing.

Reviewer #2 (Public review):

Summary:

This paper focuses on understanding the behavioral and neural basis of regime shift detection, a common yet hard problem that people encounter in an uncertain world. Using a regime-shift task, the authors examined cognitive factors influencing belief updates by manipulating signal diagnosticity and environmental volatility. Behaviorally, they have found that people demonstrate both over and under-reaction to changes given different combinations of task parameters, which can be explained by a unified system-neglect account. Neurally, the authors have found that the vmPFC-striatum network represents current belief as well as belief revision unique to the regime detection task. Meanwhile, the frontoparietal network represents cognitive factors influencing regime detection i.e., the strength of the evidence in support of the regime shift and the intertemporal belief probability. The authors further link behavioral signatures of system neglect with neural signals and have found dissociable patterns, with the frontoparietal network representing sensitivity to signal diagnosticity when the observation is consistent with regime shift and vmPFC representing environmental volatility, respectively. Together, these results shed light on the neural basis of regime shift detection especially the neural correlates of bias in belief update that can be observed behaviorally.

Strengths:

(1) The regime-shift detection task offers a solid ground to examine regime-shift detection without the potential confounding impact of learning and reward. Relatedly, the system-neglect modeling framework provides a unified account for both over or under-reacting to environmental changes, allowing researchers to extract a single parameter reflecting people's sensitivity to changes in decision variables and making it desirable for neuroimaging analysis to locate corresponding neural signals.

Thank you for recognizing our task design and our system-neglect computational framework in understanding change detection.

(2) The analysis for locating brain regions related to belief revision is solid. Within the current task, the authors look for brain regions whose activation covary with both current belief and belief change. Furthermore, the authors have ruled out the possibility of representing mere current belief or motor signal by comparing the current study results with two other studies. This set of analyses is very convincing.

Thank you for recognizing our control studies in ruling out potential motor confounds in our neural findings on belief revision.

(3) The section on using neuroimaging findings (i.e., the frontoparietal network is sensitive to evidence that signals regime shift) to reveal nuances in behavioral data (i.e., belief revision is more sensitive to evidence consistent with change) is very intriguing. I like how the authors structure the flow of the results, offering this as an extra piece of behavioral findings instead of ad-hoc implanting that into the computational modeling.

Thank you for appreciating how we showed that neural insights can lead to new behavioral findings.

Weaknesses:

(1) The authors have presented two sets of neuroimaging results, and it is unclear to me how to reason between these two sets of results, especially for the frontoparietal network. On one hand, the frontoparietal network represents belief revision but not variables influencing belief revision (i.e., signal diagnosticity and environmental volatility). On the other hand, when it comes to understanding individual differences in regime detection, the frontoparietal network is associated with sensitivity to change and consistent evidence strength. I understand that belief revision correlates with sensitivity to signals, but it can probably benefit from formally discussing and connecting these two sets of results in discussion. Relatedly, the whole section on behavioral vs. neural slope results was not sufficiently discussed and connected to the existing literature in the discussion section. For example, the authors could provide more context to reason through the finding that striatum (but not vmPFC) is not sensitive to volatility.

We thank the reviewer for the valuable suggestions.

With regard to the first comment, we wish to clarify that we did not find frontoparietal network to represent belief revision. It was the vmPFC and ventral striatum that we found to represent belief revision ( in Fig. 3). For the frontoparietal network, we identified its involvement in our task through finding that its activity correlated with strength of change evidence (Fig. 4) and individual subjects’ sensitivity to signal diagnosticity (Fig. 5). Conceptually, these two findings reflect how individuals interpret the signals (signals consistent or inconsistent with change) in light of signal diagnosticity. This is because (1) strength of change evidence is defined as signals (+1 for signal consistent with change, and -1 for signal inconsistent with change) multiplied by signal diagnosticity and (2) sensitivity to signal diagnosticity reflects how individuals subjectively evaluate signal diagnosticity. At the theoretical level, these two findings can be interpreted through our computational framework in that both the strength of change evidence and sensitivity to signal diagnosticity contribute to estimating the likelihood of change (Eqs. 1 and 2). We added a paragraph in Discussion to talk about this.

We will add on p. 35:

“For the frontoparietal network, we identified its involvement in our task through finding that its activity correlated with strength of change evidence (Fig. 4) and individual subjects’ sensitivity to signal diagnosticity (Fig. 5). Conceptually, these two findings reflect how individuals interpret the signals (signals consistent or inconsistent with change) in light of signal diagnosticity. This is because (1) strength of change evidence is defined as signals (+1 for signal consistent with change, and -1 for signal inconsistent with change) multiplied by signal diagnosticity and (2) sensitivity to signal diagnosticity reflects how individuals subjectively evaluate signal diagnosticity. At the theoretical level, these two findings can be interpreted through our computational framework in that both the strength of change evidence and sensitivity to signal diagnosticity contribute to estimating the likelihood of change (Eqs. 1 and 2).”

With regard to the second comment, we added discussion on the behavioral and neural slope comparison. We pointed out previous papers conducting similar analysis (Vilares et al., 2012; Ting et al., 2015; Yang & Wu, 2020), their findings and how they relate to our results. Vilares et al. found that sensitivity to prior information (uncertainty in prior distribution) in the orbitofrontal cortex (OFC) and putamen correlated with behavioral measure of sensitivity to prior. In the current study, transition probability acts as prior in the system-neglect framework (Eq. 2) and we found that ventromedial prefrontal cortex represents subjects’ sensitivity to transition probability. Together, these results suggest that OFC and vmPFC are involved in the subjective evaluation of prior information in both static (Vilares et al., 2012) and dynamic environments (current study). In addition, we added to the literature by showing that distinct from vmPFC in representing sensitivity to transition probability or prior, the frontoparietal network represents how sensitive individual decision makers are to the diagnosticity of signals in revealing the true state (regime) of the environment.

We will add on p. 36:

“In the current study, our psychometric-neurometric analysis focused on comparing behavioral sensitivity with neural sensitivity to the system parameters (transition probability and signal diagnosticity). We measured sensitivity by estimating the slope of behavioral data (behavioral slope) and neural data (neural slope) in response to the system parameters. Previous studies had adopted a similar approach (Vilares et al., 2012; Ting et al., 2015; Yang & Wu, 2020). For example, Vilares et al. (2012) found that sensitivity to prior information (uncertainty in prior distribution) in the orbitofrontal cortex (OFC) and putamen correlated with behavioral measure of sensitivity to the prior. In the current study, transition probability acts as prior in the system-neglect framework (Eq. 2) and we found that ventromedial prefrontal cortex represents subjects’ sensitivity to transition probability. Together, these results suggest that OFC and vmPFC are involved in the subjective evaluation of prior information in both static (Vilares et al., 2011) and dynamic environments (current study). In addition, we added to the literature by showing that distinct from vmPFC in representing sensitivity to transition probability or prior, the frontoparietal network represents how sensitive individual decision makers are to the diagnosticity of signals in revealing the true state (regime) of the environment.”

(2) More details are needed for behavioral modeling under the system-neglect framework, particularly results on model comparison. I understand that this model has been validated in previous publications, but it is unclear to me whether it provides a superior model fit in the current dataset compared to other models (e.g., a model without \alpha or \beta). Relatedly, I wonder whether the final result section can be incorporated into modeling as well - i.e., the authors could test a variant of the model with two \betas depending on whether the observation is consistent with a regime shift and conduct model comparison.

Thank you for the great suggestion.

To address the reviewer’s question on model comparison, we tested 4 variants of the system-neglect model and incorporated them into the final result section. The original system-neglect model and its four models are:

– Original system-neglect model: 6 total parameters, 3 beta parameters (one for each level of signal diagnosticity) and 3 alpha parameters (one for each level of transition probability).

– M1: System-neglect model with signal-dependent beta parameters (alpha parameters, and beta parameters separately estimated at change-consistent and change-inconsistent signals): 9 total parameters, 3 beta parameters for change-consistent signals, 3 beta parameters for change-inconsistent signals, and 3 alpha parameters.

– M2: System-neglect model with signal-dependent alpha parameters (alpha parameters separately estimated at change-consistent and change-inconsistent signals, and beta parameters): 9 total parameters, 3 alpha parameters for change-consistent signals, 3 alpha parameters for change-inconsistent signals, and 3 beta parameters.

– M3: System-neglect model without alpha parameters (only the beta parameters): 3 total parameters, all are beta parameters (one for each level of signal diagnosticity).

– M4: System-neglect model without beta parameters (only the alpha parameters): 3 total parameters, all are alpha parameters (one for each level of transition probability).

We compared these four models with the original system-neglect model. In the figure below, we plot where is the Akaike Information Criterion (AIC) of one of the new models minus the AIC of the original model. ∆AIC<0 indicates that the new model is better than the original model. By contrast, ∆AIC>0 suggests that the new model is worse than the original model.

Author response image 2.

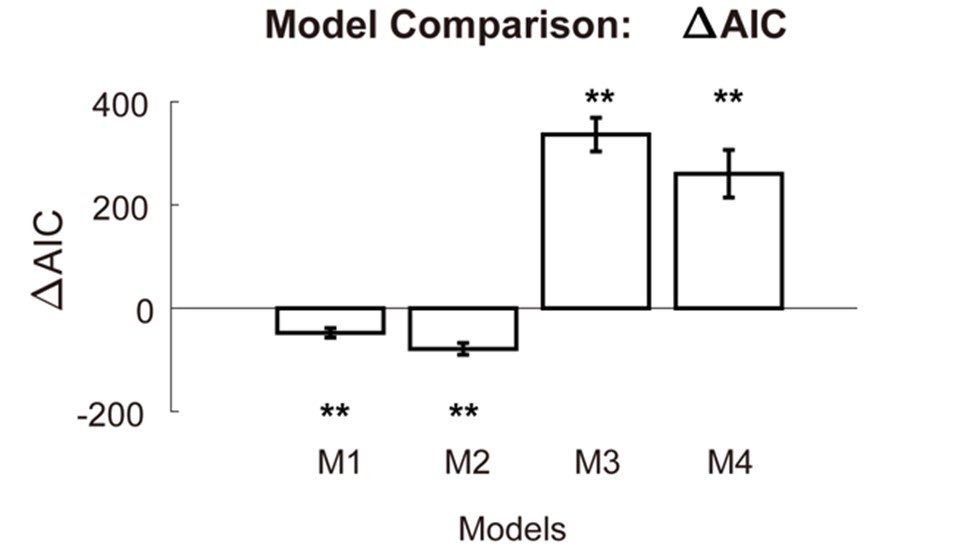
When we separately estimated the beta parameter (M1) for change-consistent signals and change-inconsistent signals, we found that its AIC is significantly smaller than the original model (p<0.01). The same was found for the model where we separately estimated the alpha parameters for change-consistent and change-inconsistent signals (M2). When we took out either the alpha (M3) or the beta parameters (M4), we found that these models were worse than the original model (p<0.01). In summary, we found that models where we separately estimated the alpha/beta parameters for change-consistent and change-inconsistent signals were better than the original model. This is consistent with the insight the neural data provided.

To show these results, we will add a new figure (Figure 7) in the revised manuscript.