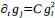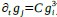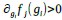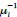The zoo of the gene networks capable of pattern formation by extracellular signaling

Reviewer #1 (Public review):

Summary:

The authors tackle a long-standing question in developmental theory: given a gene-regulatory network that includes extracellular signalling, which topologies are even capable of transforming an initial spatial profile into a genuinely new pattern? Building on the classical reaction-diffusion framework in one dimension, but imposing biologically motivated constraints, they prove that every one-signal sub-network must be either Hierarchical (H), self-activating (L+), or self-inhibiting (L-). They further demonstrate that only three composite classes of full networks - pure H, a coupled L+ L- "Turing" pair, and an L- module fed by an intracellular positive loop ("noise-amplifying")-can create non-trivial spatial transformations. Analytical criteria and illustrative simulations are provided, together providing a closed taxonomy, which is supposed to be relevant for real systems.

Strengths:

(1) Useful classification framework. Reducing a vast number of possible gene circuits to three canonical pattern-forming motifs is a valuable organising insight for both theorists and experimentalists.

(2) Logical completeness. All required cases are addressed, and the proofs elevate previous computational observations to formal statements.

(3) Practical interpretability. Given a reaction network diagram, one can now decide (assuming the model applies to the real systems) whether spatial patterning is even possible, saving experimental effort on in-silico screens that could never succeed.

Weaknesses:

(1) The Results section is difficult to follow. Key logical steps and network configurations are described shortly in prose, which constantly require the reader to address either SI or other parts of the text (see numerous links on the requirements R1-R5 listed at the beginning of the paper) to gain minimal understanding. As a result, a scientifically literate but non-specialist reader may struggle to grasp the argument with a reasonable time invested.

(2) A central step in the model formulation is the linearisation of the reaction term around a homogeneous steady state; higher-order kinetics, including ubiquitous bimolecular sinks such as A + B → AB, are simply collapsed into the Jacobian without any stated amplitude bound on the perturbations. Because the manuscript never analyses how far this assumption can be relaxed, the robustness of the three-class taxonomy under realistic nonlinear reactions or large spike amplitudes remains uncertain.

(3) All modelling is confined to one spatial dimension, and the very definition of a "non-trivial" transformation is framed in terms of peak positions along a line, which clearly must be reformulated for higher dimensions. It's well-known that diffusions in 1, 2, and 3 dimensions are also dramatically different, so the relevance of the three-class taxonomy to real multicellular tissues remains unclear, or at least should be explained in more detail.

Discussion:

As stated above, there are several uncertainties about the relevance of the presented framework for real systems. However, if the results hold, researchers could look at a gene-network diagram and quickly judge whether it can make spatial patterns and, if so, which of the three known mechanisms it will use. That shortcut would save experimental and computational time. In the case that the results don't hold for the real systems, the authors' proof tools at least give theorists a solid base they can extend to more complex cases.

Reviewer #2 (Public review):

Summary:

This study explores how gene regulatory networks that include intra- and extracellular signaling can give rise to spatial patterns of gene expression in cells. The authors investigate this question in a simplified theoretical framework, where all cells are assumed to respond identically to signals, and spatial details such as cell boundaries and extensions are abstracted away. Within this setting, they identify three distinct signaling topologies, referred to as L and H types, and combine them into three minimal subnetworks capable of generating patterns. The study analyzes possible combinations of these topologies and examines how each subnetwork behaves under three different initial conditions. Combining the analyses with mathematical proofs and heuristic arguments, the authors define necessary conditions under which such networks can produce non-trivial spatial patterns.

Strengths:

The authors break down larger gene regulatory networks into smaller subnetworks, which allows for a more tractable analysis of pattern formation. These minimal subnetworks are examined under different initial conditions, providing a range of examples for how patterns can emerge in simplified settings. The study also proposes necessary conditions for pattern formation, which may be useful for identifying relevant network structures. In addition, the manuscript offers heuristic explanations for the emergence of patterns in each subnetwork, which help to interpret the simulation results and analytical criteria.

Weaknesses:

(1) We have serious concerns regarding the validity of the simulation results presented in the manuscript. Rather than simulating the full nonlinear system described by Equation (1), the authors base their results on a truncated expansion (Equation S.8.2) that captures only the time evolution of small deviations around a spatially homogeneous steady state. However, it remains unclear how this reduced system is derived from the full equations - specifically, which terms are retained or neglected and why - and how the expansion of the nonlinear function can be steady-state independent, as claimed. Additionally, in simulations involving the spike plus homogeneous initial condition, it is not evident - or, where equations are provided, it is not correct - that the assumed global homogeneous background actually corresponds to a steady state of the full dynamics. We elaborate on these concerns in the following:

It is assumed that the homogeneous steady states are given by g_i=0 and g_i=c_i, where 1/c_i = \mu_i or \hat{\mu}_i​, independently of the specific network structure. However, the basis for this assumption is unclear, especially since some of the functions do not satisfy this condition - for example, f5​ as defined below Eq. S8.10.5. Moreover, if g_i=c_i does not correspond to a true steady state, then the time evolution of deviations from this state is not correctly described by Eq. S8.2, as the zeroth-order terms do not vanish in that case.

Additionally, the equations used contain only linear terms and a cubic degradation term for each species g_i, while neglecting all quadratic terms and cubic terms involving cross-species interactions (i≠j). An explanation for this selective truncation is not provided, and without knowledge of the full equation (f), it is impossible to assess whether this expansion is mathematically justified. If, as suggested in the Supplementary Information, the linear and cubic terms are derived from f, then at the very least, the Jacobian matrix should depend on the background steady-state concentration. However, the equations for the small deviation around a steady state (including the Jacobian matrix) used in the simulations appear to be independent of the particular steady state concentration.

This is why we believe that the differences observed between the spike-only initial condition and the spike superimposed on a homogeneous background are not due to the initial conditions themselves, but rather result from a modified reaction scheme introduced through a questionable cutoff.

"In simulations with spike initial patterns, the reference value g≡0 represents an actual concentration of 0 and therefore, we must add to (S8.2) a Heaviside function Φ acting of f (i.e., Φ(f(g))=f(g) if f(g)>0 , Φ(f(g))=0 if f(g){less than or equal to}0 ) to prevent the existence of negative concentrations for any gene product (i.e., g_i<0 for some i )." (SI chapter S8).

This cutoff alters the dynamics (no inhibition) and introduces a different reaction scheme between the two simulations. The need for this correction may itself reflect either a problem in the original equations (which should fulfill the necessary conditions and prevent negative concentrations (R4 in main text)) or the inappropriateness of using an expanded approximation which assumes independence on the steady state concentration. It is already questionable if the linearized equations with a cubic degradation term are valid for the spike initial conditions (with different background concentration values), as the amplitude of this perturbation seems rather large.

Lastly, we note that under the current simulation scheme, it is not possible to meaningfully assess criteria RH2a and RH2b, as they rely on nonlinear interactions that are absent from the implemented dynamics.

(2) Most of the proofs presented in the Supplementary Information rely on linearized versions of the governing equations, and it remains unclear how these results extend to the fully nonlinear system. We are concerned that the generality of the conclusions drawn from the linear analysis may be overstated in the main text. For example, in Section S3, the authors introduce the concept of dynamic equivalence of transitive chains (Proposition S3.1) and intracellular transitive M-branching (Proposition S3.2), which pertains to the system's steady-state behavior. However, the proof is based solely on the linearized equations, without additional justification for why the result should hold in the presence of nonlinearities. Moreover, the linearized system is used to analyze the response to a "spike initial pattern of arbitrary height C" (SI Chapter S5.1), yet it is not clear how conclusions derived from the linear regime can be valid for large perturbations, where nonlinear effects are expected to play a significant role. We encourage the authors to clarify the assumptions under which the linearized analysis remains valid and to discuss the potential limitations of applying these results to the nonlinear regime.

(3) Several statements in the main text are presented without accompanying proof or sufficient explanation, which makes it difficult to assess their validity. In some cases, the lack of justification raises serious doubts about whether the claims are generally true. Examples are:

"For the purpose of clarity we will explain our results as if these cells have a simple arrangement in space (e.g., a 1D line or a 2D square lattice) but, as we will discuss, our results shall apply with the same logic to any distribution of cells in space." (Main text l.145-l.148).

"For any non-trivial pattern transformation (as long as it is symmetric around the initial spike), there exists an H gene network capable of producing it from a spike initial pattern." (Main text l.366f).

"In 2D there are no peaks but concentric rings of high gene product concentration centered around the spike, while in 3D there are concentric spherical shells." (Main text l. 447ff).

(4) The study identifies one-signal networks and examines how combinations of these structures can give rise to minimal pattern-forming subnetworks. However, the analysis of the combinations of these minimal pattern-forming subnetworks remains relatively brief, and the manuscript does not explore how the results might change if the subnetworks were combined in upstream and downstream configurations. In our view, it is not evident that all possible gene regulatory networks can be fully characterized by these categories, nor that the resulting patterns can be reliably predicted. Rather, the approach appears more suited to identifying which known subnetworks are present within a larger network, without necessarily capturing the full dynamics of more complex configurations.

(5) The definition of non-trivial pattern formation is provided only in the Supplementary Information, despite its central importance for interpreting the main results. It would significantly improve clarity if this definition were included and explained in the main text. Additionally, it remains unclear how the definition is consistently applied across the different initial conditions. In particular, the authors should clarify how slope-based measures are determined for both the random noise and sharp peak/step function initial states. Furthermore, the authors do not specify how the sign function is evaluated at zero. If the standard mathematical definition sgn(0)=0 is used, then even a simple widening of a peak could fulfill the criterion for non-trivial pattern transformation.

(6) The manuscript lacks a clear and detailed explanation of the underlying model and its assumptions. In particular, it is not well-defined what constitutes a "cell" in the context of the model, nor is it justified why spatial features of cells - such as their size or boundaries - can be neglected. Furthermore, the concept of the extracellular space in the one-dimensional model remains ambiguous, making it unclear which gene products are assumed to diffuse.

Reviewer #3 (Public review):

Pattern formation is responsible for generating the spatial organization of cells, tissues, and organs during embryogenesis. It operates within a multifactorial system including initial conditions, gene regulatory networks, extracellular signals, mechanical forces, stochastic noise, and environmental inputs. Finally, it ensures the functional anatomy of an organism.

This study focuses on the one central aspect in pattern formation: how spatial heterogeneity arises from an initial condition and evolves into a more complex or distinct spatial pattern (non-trivial pattern formation, as they termed). The authors made efforts to explore and characterize all possible ways to achieve the pattern formation. They do this by discussing how extracellular signals spread, how individual cells respond to those signals, and how those responses, in turn, modulate signal propagation.

Finally, their comprehensive analysis summarizes that there are three classes of interactions between extracellular signals and intracellular responses, corresponding to previously known mechanisms that can generate spatial patterns: difference in morphogen concentrations in space, noise-amplification, and Turing pattern.

Author response:

We thank the reviewers for their thorough evaluation and constructive feedback on our manuscript.

We think that their valuable suggestions will strengthen the manuscript and help us clarify several important points.

All reviewers acknowledged the importance of our theoretical results and network classification in making pattern formation analysis a more tractable problem. At the same time, they have also raised a number of important concerns that we shall carefully consider.

A. A major clarification that the reviewers found important concerns the definition of non-trivial pattern transformations and its generalization to higher dimensions. In this regard, the reviewers’ comments are:

Reviewer #1:

(on non-trivial pattern transformations):

(3) All modelling is confined to one spatial dimension, and the very definition of a "non-trivial" transformation is framed in terms of peak positions along a line, which clearly must be reformulated for higher dimensions. It's well-known that diffusions in 1, 2, and 3 dimensions are also dramatically different, so the relevance of the three-class taxonomy to real multicellular tissues remains unclear, or at least should be explained in more detail. Reviewer #2 (on non-trivial pattern transformations):

(5) The definition of non-trivial pattern formation is provided only in the Supplementary Information, despite its central importance for interpreting the main results. It would significantly improve clarity if this definition were included and explained in the main text. Additionally, it remains unclear how the definition is consistently applied across the different initial conditions. In particular, the authors should clarify how slope-based measures are determined for both the random noise and sharp peak/step function initial states. Furthermore, the authors do not specify how the sign function is evaluated at zero. If the standard mathematical definition sgn(0)=0 is used, then even a simple widening of a peak could fulfill the criterion for nontrivial pattern transformation.

We agree with Reviewer #2 that including a more detailed definition of non-trivial pattern transformation in the main text would enhance the clarity of the paper. The one-dimensional (1D) definition currently provided in the Supplementary Information was chosen because all computations presented therein involve exclusively one-dimensional patterns. However, we acknowledge that this definition, as it was, did not have a totally unambiguous generalization to higher dimensions. Therefore, in a revised version of the manuscript, we will incorporate an expanded definition applicable to higher-dimensional cases.

This general definition of a non-trivial pattern transformation should make no reference to the sign of spatial derivatives of either the initial or resulting patterns. Specifically, a pattern transformation is considered non-trivial if it satisfies the following criteria:

- It is heterogeneous: The resulting pattern is heterogeneous in space.

- It is rearranging: The arrangement of critical points (i.e. peaks, valleys and saddle points in a gene product concentration) along the domain in the resulting pattern of a gene product is different to the arrangement of critical points in its initial pattern. This includes the emergence of new critical points, the disappearance of existing ones, or the spatial displacement of critical points from one location to another.

- It is non-replicating: The spatial arrangement of critical points in the pattern of one gene product must differ from that of any other upstream gene product.

Nonetheless, our two initial patterns are spatially discontinuous functions: in homogeneous initial patterns, the white noise is discontinuous by definition; and for the spike and spike+homogeneous initial patterns, we use sharp spikes defined by the rectangular function, which is discontinuous at the spike boundaries. Therefore, the aforementioned definition should be supplemented with the following two ad hoc assumptions:

- Homogeneous initial patterns do not comprise any critical point. White noise in this type of initial patterns represents small thermodynamic fluctuations around the steady state and, for the purpose of pattern transformation, this is equivalent to a constant concentration along the domain.

- Spike and spike+homogeneous initial patterns each contain a single critical point located at the center of the spike. The sharp spikes, modeled using the rectangular function, serve as a theoretical idealization to facilitate mathematical analysis. Once diffusion begins to act, these sharp boundaries are smoothed into differentiable gradients, maintaining a unique critical point at the center of the initial spike, which is the most relevant information for pattern transformation.

Finally, it is worth recalling that our gene network classification is fundamentally based on an analysis of the dispersion relation associated with the gene network, and the construction of this dispersion relation is independent of the spatial dimensionality of the domain (i.e. it does not require assuming any specific number of dimensions). The fact that the description of this dispersion relation was in the SI may have been non-ideal for the understandability of the article and will, consequently, be moved to the main text in an upcoming version of the article. Thus, the gene networks that can lead to pattern transformation are the same in 1D, 2D or 3D. As for the resulting patterns, the broad description we provide also applies to any number of dimensions; these would be periodic, non periodic as in the amplified noise patterns or non periodic as in the hierarchic networks. For the latter notice that, except for boundary effects that we later discuss, the spike initial condition is radially symmetric and thus, the patterns resulting from it will also be radially symmetric. We will make this point more explicit in a revised version of the article, especially since, as suggested, this important portion of the Supplementary Information will be incorporated into the main text.

Reviewer 2 suggests that with our definition of non-trivial pattern transformation, the simple widening of a concentration peak would constitute a non-trivial pattern transformation. This is not the case, as already shown in the figures as a example, since in a widening there is no change in the position of the critical point. A different situation applies if a wide and completely flat concentration peak (i.e. a plateau) forms. As we will explain in the coming version this is not possible because of requirement R5.

We think that this clarification of the definition of non-trivial pattern transformation will also help clarify the next point (B below) since it would make it clearer that this article does not intend to explain which specific resulting pattern would arise from any given gene network.

B. The main concern among these relates to the validity of our linearization of the model equations and the extension of the results obtained for the linear system to the fully nonlinear system. In this regard, the reviewers’ comments are:

Reviewer #1:

(on linearization):

(2) A central step in the model formulation is the linearisation of the reaction term around a homogeneous steady state; higher-order kinetics, including ubiquitous bimolecular sinks such as A + B → AB, are simply collapsed into the Jacobian without any stated amplitude bound on the perturbations. Because the manuscript never analyses how far this assumption can be relaxed, the robustness of the three-class taxonomy under realistic nonlinear reactions or large spike amplitudes remains uncertain.

Reviewer #2:

(on linearization):

(2) Most of the proofs presented in the Supplementary Information rely on linearized versions of the governing equations, and it remains unclear how these results extend to the fully nonlinear system. We are concerned that the generality of the conclusions drawn from the linear analysis may be overstated in the main text. For example, in Section S3, the authors introduce the concept of dynamic equivalence of transitive chains (Proposition S3.1) and intracellular transitive M-branching (Proposition S3.2), which pertains to the system's steady-state behavior. However, the proof is based solely on the linearized equations, without additional justification for why the result should hold in the presence of nonlinearities. Moreover, the linearized system is used to analyze the response to a "spike initial pattern of arbitrary height C" (SI Chapter S5.1), yet it is not clear how conclusions derived from the linear regime can be valid for large perturbations, where nonlinear effects are expected to play a significant role. We encourage the authors to clarify the assumptions under which the linearized analysis remains valid and to discuss the potential limitations of applying these results to the nonlinear regime.

In this article, we address two main questions: first, which gene network topologies can give rise to non-trivial pattern transformations; and second, which broad types of resulting patterns can these gene network topologies give rise to resulting pattern. Thus, we are not intending to explain which exact resulting patterns would arise from any given gene network (i.e. a gene network topology with specific functions and interaction strengths or weights), a question for which non-linearities do indeed matter.

For most known gene regulatory networks, available empirical information is typically limited to the nature of gene product regulations -indicating whether they act as activators or inhibitors- while details about the specific functional form of these regulations are rare. For instance, given two gene products, i and j, the network may indicate that i acts as an activator of j, implying that the concentration of j increases with that of i. However, this increase could follow a variety of functional forms: it may be quadratic (e.g., 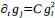), cubic (e.g., 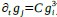), or any other function f j(gi). As we explain in the description of our model, we restrict our study to functions with a monotonicity constraint: higher concentrations of i lead to increased production of j (i.e., 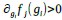). In other words, a given gene interaction is always inhibitory or activatory, it does not change of sign. This monotonicity constraint corresponds to requirement (R5) in our main text. This requirement it is based on the biologically plausible idea that the complexity of gene regulation in development stems more from the topology of gene networks than from the complexity of the regulation by which a gene product may regulate another (i.e. we use simple monotonic functions).

Question 1: A critical part to understand question 1 is in the dispersion relation that was explained in SI. From the reviewers’ comments it is clear that having this crucial part in the main text of an upcoming version of the article would improve understandability, specially for question 1.

In brief, any pattern transformation requires the initial pattern to change. The trigger of such change is a change in the concentration of some gene product, either conceptualized as a noise fluctuation (in the homogeneous initial pattern) or a regulated change in a specific point (in the spike initial pattern). Mathematically, both can be conceptualized as perturbations and, for pattern transformation to be possible, such perturbation should grow so that the initial pattern becomes unstable and can change to another resulting pattern.

If the perturbation is small, one can use the standard linear perturbation analysis in S6.2 of our Supplementary Information. In other words, the linear analysis is enough to ascertain if a small perturbation would grow or not. A gene network in which this will not happen would be unable to lead to pattern transformation, whichever the nonlinear part of f(g). In that sense, the linear approximation provides a necessary condition that any gene network needs to fulfill to lead to pattern transformation.

However, the linear analysis would not ascertain whether a specific gene network will actually lead to pattern transformation (i.e., the condition is not sufficient). This, as well as the shape of the specific resulting pattern, may actually depend on the non-linear parts too. As we discuss, based on the dispersion relation, and other complementing arguments along the article, we can also get some insights on the possible patterns from the linear approximation alone (question 2). This arguments hold thanks to the imposition of requirements (R1-R5) on function f(g), which prevent strange behaviors stemming from the nonlinear part of the equation.

The amplitude bound of perturbations mentioned by Reviewer #1 is addressed by requirements (R2) and (R4). Although the solution to the linear system predicts unbounded growth of unstable eigenmodes, the assume functions f(g) on which the nonlinear terms eventually halt this growth, thereby ensuring the boundedness of solutions as imposed by (R4). This assumption on the nonlinear part is literally requirement R2 on f(g) in the main text.

The transitive chains and branchings in section S3 of the Supplementary Information mentioned by the Reviewer #2 are topological properties of gene networks and therefore they influence only the linear part of the reaction-diffusion equations. This is why the proofs in that section are based on the linearized equations. We agree that clarifying this point in the text, as suggested by the reviewer, would improve the reader’s understanding of the section.

Regarding Reviewer #2’s concerns about large perturbations, we acknowledge that the phrasing using “arbitrary height” may be confusing. For the homogeneous initial conditions these perturbations are assumed to be small because they are actually molecular noise (otherwise the initial condition could not be considered homogenous in the classical sense of developmental biology models). In the spike initial conditions in hierarchic networks the perturbation is not necessarily small. For the analysis provided in the SI we indeed assume that the perturbations are small enough for the linear approximation to be possible. Notice, however, that since these networks require an intracellular self-activating loop upstream of the first extracellular signal, the effective perturbation would rapidly grow to a value determined by such loop.

In general the height of the initial spike does not affect the fact that hierarchic networks can lead to non-trivial pattern transformation. By definition these networks require the secretion of an extracellular signal from the cells in the spike (otherwise no change in gene product concentrations can occur over space). By definition this signal is not produced by any other cells and, thus, its concentration is governed by diffusion from the spike and its production in the cells in the spike. Thus, whichever the initial height of the spike and whichever the non-linearities in f(g), the signal’s concentration would decrease with the distance from the spike. As explained in the main text, this would lead to non-trivial pattern transformations if other general conditions are met. In general, the height of the initial perturbation can affect which specific pattern transformation would arise from a specific gene network but not which gene network topologies can lead to pattern transformation. This will be more clearly stated in an upcoming version of the article. C. In the following, we respond to the remaining concerns raised by the reviewers:

Reviewer #1:

(1) The Results section is difficult to follow. Key logical steps and network configurations are described shortly in prose, which constantly require the reader to address either SI or other parts of the text (see numerous links on the requirements R1-R5 listed at the beginning of the paper) to gain minimal understanding. As a result, a scientifically literate but non-specialist reader may struggle to grasp the argument with a reasonable time invested.

We acknowledge that the current version of the main text may not be as clear as we intended. Initially, we believed that placing the more technical mathematical passages in the Supplementary Information would make the main text more accessible to readers. However, we agree with the reviewer that including some of these computations in the main text could improve clarity. We also believe that adding a summary table outlining all the model’s requirements would further contribute to that goal.

Reviewer #2:

(1) We have serious concerns regarding the validity of the simulation results presented in the manuscript. Rather than simulating the full nonlinear system described by Equation (1), the authors base their results on a truncated expansion (Equation S.8.2) that captures only the time evolution of small deviations around a spatially homogeneous steady state. However, it remains unclear how this reduced system is derived from the full equations specifically, which terms are retained or neglected and why- and how the expansion of the nonlinear function can be steady-state independent, as claimed. Additionally, in simulations involving the spike plus homogeneous initial condition, it is not evident -or, where equations are provided, it is not correct- that the assumed global homogeneous background actually corresponds to a steady state of the full dynamics. We elaborate on these concerns in the following:

We believe there has been a misunderstanding regarding the presentation of the model equations (S8.2) used throughout our simulations. Accordingly, we agree that this relevant section of the Supplementary Information should be rewritten in a revised version of the manuscript to clarify this issue. Below, we address all the concerns raised by the reviewer.

Equation (S8.2) represents the full nonlinear system described in Equation (1). While we recognize that the model may oversimplify real biological processes, its purpose is to illustrate our general statements about pattern formation rather than to capture any specific or detailed mechanism. In this context, model (S8.2) offers three key advantages for our goals: it allows rapid manipulation of gene network topology simply by modifying the matrix J, making it ideal for illustrating pattern formation across different network classes; it accommodates gene networks of arbitrary size -unlike other models, such as the classical Gierer-Meinhardt model, which are limited to two-element Turing or noise-amplifying networks-; and, due to the simplicity of its nonlinear terms, this model involves relatively few free parameters, facilitating the fine-tuning needed to identify parameter regions where non-trivial pattern transformations occur.

Indeed, we find that the ability of model (S8.2) to illustrate our results despite having such simple nonlinear terms -bearing in mind that at least some nonlinearity is always necessary for selforganization- strongly supports the claim that the capacity of a gene network to produce pattern transformations is fully determined by the linear part of Equation (1). In this sense, nonlinear terms primarily influence the precise parameter values at which these transformations occur and contribute to shaping specific features of the resulting patterns.

Model (S8.2) has been successfully employed in pattern formation studies elsewhere in the literature; accordingly, we provide relevant bibliographic references to support its widespread use.

We believe the misunderstanding arises from our explanation of the biological interpretation of the model. As noted in the accompanying bibliography, the model is based on a general reactiondiffusion mechanism assuming the existence of a steady state. However, this conceptual reactiondiffusion framework is not the same as our Equation (1); rather, it was introduced by the original proponents of the model in the seminal paper cited in our text. In this context, Equation (S8.2) describes small concentration perturbations around that steady state, where the variables represent deviations in concentration relative to the general steady state.

The aforementioned general steady state corresponds to the trivial equilibrium point g≡0 in equations (S8.2). Consequently, all our simulations based on model (S8.2) start from this steady state, to which we add white noise to generate homogeneous initial patterns or a sharp spike for the two types of spike initial patterns.

It is also worth noting that Equations (S8.2) represent a non-dimensional model.

It is assumed that the homogeneous steady states are given by g_i=0 and g_i=c_i, where 1/c_i = \mu_i or \hat{\mu}_i, independently of the specific network structure. However, the basis for this assumption is unclear, especially since some of the functions do not satisfy this condition -for example, f5 as defined below Eq. S8.10.5. Moreover, if g_i=c_i does not correspond to a true steady state, then the time evolution of deviations from this state is not correctly described by Eq. S8.2, as the zeroth-order terms do not vanish in that case.

From the explanations above, it is important to distinguish two scales in the process: the scale of small perturbations, where equations (S8.2) apply; and the global scale, where the conceptual general reaction-diffusion system operates. Since the specific form of this general system does not affect equations (S8.2), we assume that it follows any of the models cited in the text, which yield a non-zero steady state at .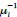

In this sense, Equation (S8.2) represent a small concentration deviation of such global system and g(t ,x) is a relative concentration where g≡0 represents the steady-state at 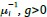are concentrations above 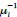, and g<0 are concentrations below .

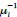As previously mentioned, simulations are performed using Equations (S8.2) on the basis of the equilibrium point g≡0. The result of these simulations is then superimposed on the non-zero steady state 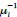and presented in the figures along the article.

Using the full model instead of the simplified Equations (S8.2) may result in slightly different resulting patterns, but it does not affect the gene network’s ability to produce pattern transformations, nor does it alter the main structural properties of the patterns—for example, the periodic nature of patterns generated by Turing networks.

Additionally, the equations used contain only linear terms and a cubic degradation term for each species g_i, while neglecting all quadratic terms and cubic terms involving cross-species interactions (i≠j). An explanation for this selective truncation is not provided, and without knowledge of the full equation (f), it is impossible to assess whether this expansion is mathematically justified. If, as suggested in the Supplementary Information, the linear and cubic terms are derived from f, then at the very least, the Jacobian matrix should depend on the background steady-state concentration. However, the equations for the small deviation around a steady state (including the Jacobian matrix) used in the simulations appear to be independent of the particular steady state concentration.

The Jacobian of Equation (S8.2) is independent of g because g represents a small perturbation around a steady state of a general reaction-diffusion system. Consequently, the matrix J corresponds to the Jacobian of the general system evaluated at that steady state. Evaluating the Jacobian of equations (S8.2) at the equilibrium point g≡0 -which represents the general steady state- recovers the matrix J.

This is why we believe that the differences observed between the spike-only initial condition and the spike superimposed on a homogeneous background are not due to the initial conditions themselves, but rather result from a modified reaction scheme introduced through a questionable cutoff.

"In simulations with spike initial patterns, the reference value g≡0 represents an actual concentration of 0 and therefore, we must add to (S8.2) a Heaviside function Φ acting of f (i.e., Φ(f(g))=f(g) if f(g)>0 , Φ(f(g))=0 if f(g){less than or equal to}0 ) to prevent the existence of negative concentrations for any gene product (i.e., g_i<0 for some i )." (SI chapter S8).

This cutoff alters the dynamics (no inhibition) and introduces a different reaction scheme between the two simulations. The need for this correction may itself reflect either a problem in the original equations (which should fulfill the necessary conditions and prevent negative concentrations (R4 in main text)) or the inappropriateness of using an expanded approximation which assumes independence on the steady state concentration. It is already questionable if the linearized equations with a cubic degradation term are valid for the spike initial conditions (with different background concentration values), as the amplitude of this perturbation seems rather large.

For homogeneous and spike+homogeneous initial conditions, we interpret equations (S8.2) as small perturbations around a non-zero steady state of a general reaction-diffusion system. For spike-only initial conditions, that steady state is zero. As we mention before, g≡0 will then represent such steady-state of zero concentration, g>0 are positive concentrations of the general system, and g<0 would represent unfeasible negative concentrations of the general system. Therefore, the use of a cutoff function to handle such initial conditions is justified. Moreover, this cutoff function is the same as the one employed in the reference general system cited in our paper.

We acknowledge that the cutoff influences the simulations and accounts for the differences observed between spike and spike+homogeneous initial conditions. However, this distinction reflects what occurs in real biological systems, which is precisely why we differentiate these two types of initial states. For instance, the emergence of a periodic pattern in a noise-amplifying network depends critically on the formation of regions with concentrations below the steady state near the initial spike. Such regions can form in spike-plus-homogeneous initial patterns but not in spike-only initial patterns, where concentrations below the steady state would correspond to biologically unfeasible negative values.

Lastly, we note that under the current simulation scheme, it is not possible to meaningfully assess criteria RH2a and RH2b, as they rely on nonlinear interactions that are absent from the implemented dynamics.

It is explicitly stated in the relevant subsections of Section S7 in the Supplementary Information that, for the simulations involving RH2a and RH2b, the function f(g) in equation (S8.2) is modified by adding an ad hoc quadratic term to enable the assessment of these criteria.

(3) Several statements in the main text are presented without accompanying proof or sufficient explanation, which makes it difficult to assess their validity. In some cases, the lack of justification raises serious doubts about whether the claims are generally true. Examples are:

"For the purpose of clarity we will explain our results as if these cells have a simple arrangement in space (e.g., a 1D line or a 2D square lattice) but, as we will discuss, our results shall apply with the same logic to any distribution of cells in space." (Main text l.145-l.148).

We believe that the confusion in this statement arises from the ambiguous use of the phrase “our results”. We will revise the text to provide a more precise description. Specifically, by “our results,” we refer to the conclusion that it is possible to determine whether a gene network leads to nontrivial pattern transformations based solely on its topology. This conclusion is independent of the dimensionality of space, as none of our arguments rely on assumptions specific to spatial dimensions. While one-dimensional examples are used for clarity and illustration, the underlying reasoning applies generally. In an improved version of the article, we will clarify this point explicitly and move relevant arguments from the Supplementary Information into the main text.

Critically, our classification of gene networks is ultimately based on an argument concerning the dispersion relation associated with the network, and the construction of this dispersion relation is independent of the spatial dimensionality of the domain. In this sense, the networks identified in the text as capable of producing pattern transformations will be able to generate non-trivial pattern transformations in any spatial domain and in any number of dimensions. While the specific parameter values that permit such transformations may vary depending on the geometry and dimensionality of the domain, the existence of at least one such parameter set remains unaffected.

The geometry of the domain can influence the specific form of the resulting patterns, but it does not alter the broader class of patterns (e.g., periodic patterns, peaks emerging around a spike, etc.) that a given gene network topology can produce. One such geometric influence, commonly observed in simulations, involves boundary effects. For example, structures such as peaks or rings forming near the boundaries may appear higher, broader, or spatially shifted compared to those arising in the central regions of the domain. However, we think a pattern consisting of a periodic train of peaks where only those near the boundary are slightly different can still be classified as a periodic pattern.

"For any non-trivial pattern transformation (as long as it is symmetric around the initial spike), there exists an H gene network capable of producing it from a spike initial pattern." (Main text l.366f).

A justification for this statement is provided shortly after the claim, although we acknowledge that the current explanation is somewhat cumbersome and would benefit from a clearer presentation in a revised version of the main text.

A more detailed justification is provided in the Supplementary Information, based on three key ideas. First, any pattern (provided it is symmetric with respect to the initial spike) can be described as an arrangement of peaks with varying heights and spatial positions along a one-dimensional domain. Second, there exists a simple gene network—the diamond network—that, through parameter tuning, can produce two peaks of arbitrary height and symmetric position relative to the initial spike. Third, by placing multiple diamond networks positively upstream of a common gene product, that gene product can express peaks at each location where the upstream diamond networks induce them. Under mild additional conditions, this mechanism allows the formation of essentially any symmetric pattern. These mild conditions, along with a detailed analysis of the diamond network’s ability to generate peaks with controllable height and position, are discussed in the Supplementary Information.

"In 2D there are no peaks but concentric rings of high gene product concentration centered around the spike, while in 3D there are concentric spherical shells." (Main text l. 447ff).

This result pertains specifically to pattern transformations arising from spike initial patterns. As defined in the text, spike initial patterns are radially symmetric. Since diffusion preserves radial symmetry, pattern transformations from spike initial patterns in two or three dimensions reduce to effectively one-dimensional transformations along each radial direction. In this framework, each pair of concentration peaks symmetric with respect to the spike in one dimension corresponds to a ring surrounding the spike in two dimensions, and each ring in two dimensions becomes a hollow spherical shell around the spike in three dimensions.

We agree that including a brief section in the Supplementary Information to clarify these subtleties would be helpful for readers to better understand the generalization of certain patterns to higher dimensions.

(4) The study identifies one-signal networks and examines how combinations of these structures can give rise to minimal pattern-forming subnetworks. However, the analysis of the combinations of these minimal pattern-forming subnetworks remains relatively brief, and the manuscript does not explore how the results might change if the subnetworks were combined in upstream and downstream configurations. In our view, it is not evident that all possible gene regulatory networks can be fully characterized by these categories, nor that the resulting patterns can be reliably predicted. Rather, the approach appears more suited to identifying which known subnetworks are present within a larger network, without necessarily capturing the full dynamics of more complex configurations.

We acknowledge that our explanation regarding the combination of sub-networks was relatively brief, and we intend to address this in a revised version. Our argument that combining sub-networks does not produce qualitatively new types of pattern transformations -beyond those already described- is based on the dispersion relation. Although this relation was only detailed in the Supplementary Information, it is central to our argument and will therefore be moved to the main text. Below, we provide an outline of this argument:

Our study identifies two distinct behaviors of the principal branch of the dispersion relation at large wavenumbers. Based on this, gene networks capable of pattern formation can be classified into two categories: networks of the first kind, where the real part of the principal branch diverges to infinity as the wavenumber increases; and networks of the second kind, where the real part of the principal branch converges to a positive finite value for large wavenumbers. Naturally this argument applies to any gene network irrespectively of which, or how many, sub-networks are used to built it.

Any gene regulatory network capable of pattern formation falls into one of these two categories. We identified that networks of the first kind contain at least one Turing sub-network, whereas networks of the second kind include either an H sub-network or a noise-amplifying sub-network. In this way, the primary objective of our study -namely, achieving a topological classification of gene regulatory networks capable of pattern formation- is fulfilled. It is important to note that while the dispersion relation provides broad information about the possible resulting patterns a gene network topology can produce (e.g., periodic versus noisy), it does not specify the exact patterns that emerge for each particular set of parameter values.

Finally, regarding the shape of the resulting patterns, Figure S10 in the Supplementary Information exemplifies the notion that the behavior of combined networks can be understood as a combination of the individual behaviors of each constituent sub-network (note that the contribution of each type of sub-network in the resulting pattern is readily distinguishable). Consequently, we focus our detailed analysis on the patterning properties of the fundamental classes.

(6) The manuscript lacks a clear and detailed explanation of the underlying model and its assumptions. In particular, it is not well-defined what constitutes a "cell" in the context of the model, nor is it justified why spatial features of cells -such as their size or boundaries- can be neglected. Furthermore, the concept of the extracellular space in the one-dimensional model remains ambiguous, making it unclear which gene products are assumed to diffuse.

The size of cells is ignored in our model because we assume that they are small enough with respect to the total size of the domain that the space continuous reaction-diffusion equation (equation (1) in the main text) holds. Conceptually, one could understand cells in our model each of the pieces in an even partition of the domain into small subdomains surrounding each position x. This is anyway the standard procedure in most models of pattern formation by reaction-diffusion in embryonic development.

For extracellular signals, we assume that g(t ,x) corresponds to the concentration of the signal in the extracellular space surrounding the cell located at position x. The extracellular space is any fluid medium for which Fick Laws apply and, therfore, the Fickian diffusion term in equation (1) is valid.

For intracellular gene products, we assume that g(t ,x) corresponds to the concentration of such gene product within the cell at position x (if the gene product in hand is a transcription factor, for example), or on its surface (if it is a membrane-bound receptor). When collapsed in the continuous equations there is not such difference between being strictly within the cell or on its boundary. The only important fact is that these gene products cannot diffuse.

Regarding cell boundaries, let us consider an extracellular signal s that regulates a transcriptor factor i within cells (in our model, i is an intracellular gene product). Such regulation shall be mediated by a membrane-bound receptor, which corresponds to intracellular gene product j. In terms of the gene regulatory network this is s→ j→i. Cell boundary effects mentioned by the reviewer should be encapsulated in the specific functional form of the regulation function f(g), but they have no effect in the actual topology of the network. Consequently, they are out of the scope of this study: as we mentioned before, considering different non-linear terms for f(g) will affect the parameter range for which a gene network is capable of producing non-trivial pattern transformations, but not their overall ability to produce non-trivial pattern transformations (i.e., the existence of at least one choice of model parameters for which such transformations take place).

Finally, we would like to once again express our sincere gratitude to all reviewers for their insightful and constructive feedback. We are confident that the thorough peer review process will significantly enhance both the clarity and depth of our work. We greatly value the detailed comments provided and will carefully incorporate them in the preparation of a revised manuscript, which we intend to submit in the coming months.