Author Response
Reviewer #1 (Public Review):
The authors introduce a computational model that simulates the dendrites of developing neurons in a 2D plane, subject to constraints inspired by known biological mechanisms such as diffusing trophic factors, trafficked resources, and an activity-dependent pruning rule. The resulting arbors are analyzed in terms of their structure, dynamics, and responses to certain manipulations. The authors conclude that 1) their model recapitulates a stereotyped timecourse of neuronal development: outgrowth, overshoot, and pruning 2) Neurons achieve near-optimal wiring lengths, and Such models can be useful to test proposed biological mechanisms- for example, to ask whether a given set of growth rules can explain a given observed phenomenon - as developmental neuroscientists are working to understand the factors that give rise to the intricate structures and functions of the many cell types of our nervous system.
Overall, my reaction to this work is that this is just one instantiation of many models that the author could have built, given their stated goals. Would other models behave similarly? This question is not well explored, and as a result, claims about interpreting these models and using them to make experimental predictions should be taken warily. I give more detailed and specific comments below.
We thank the reviewer for the summary of the work. We find the criticism “that this is one instantiation of many models [we] could have built” can apply to any model. To quote George Box, “all models are wrong, but some models are useful” was the moto that drove our modeling approach. In principle, there are infinitely many possible models. We chose one of the most minimalistic models which implements known biological mechanisms including activity-independent and -dependent phases of dendritic growth, and constrained parameters based on experimental data. We compare the proposed model to other alternatives in the Discussion section, especially to the models of Hermann Cuntz which propose very different strategies for growth.
However, the reviewer is right that within the type of model we chose, we could have more extensively explored the sensitivity to parameters. In the revised manuscript we will investigate the sensitivity of model output to variations of specific parameters, as explained below.
Point 1.1. Line 109. After reading the rest of the manuscript, I worry about the conclusion voiced here, which implies that the model will extrapolate well to manipulations of all the model components. How were the values of model parameters selected? The text implies that these were selected to be biologically plausible, but many seem far off. The density of potential synapses, for example, seems very low in the simulations compared to the density of axons/boutons in the cortex; what constitutes a potential synapse? The perfect correlations between synapses in the activity groups is flawed, even for synapses belonging to the same presynaptic cell. The density of postsynaptic cells is also orders of magnitude of, etc. Ideally, every claim made about the model's output should be supported by a parameter sensitivity study. The authors performed few explorations of parameter sensitivity and many of the choices made seem ad hoc.
It is indeed important to clarify how the model parameters were selected. Here we provide a short justification for some of these parameters, which will be included in the revised manuscript.
- Potential synapse density: We modelled 1,500 potential synapses in a cortical sheet of size 185x185 microns squared. We used 1 pixel per μm to capture approximately 1 μm thick dendrites. Therefore, we started with initial density of 0.044 potential synapses per μm^2. From Author Response Image 1 we can see that at the end of our simulation time ~1,000 potential synapses remain. So in fact, the density of potential synapses is totally sufficient, since not many potential synapses end up connected. The rapid slowing down of growth in our model is not due to a depletion of potential synaptic partners as the number of potential synapses remains high. Nonetheless, we will explore this in the revised manuscript. (this figure will be included in the revised submission):
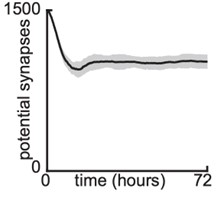
- Stabilized synapse density: Since ~1,000 of the potential synapses in the modeled cortical sheet remain available, ~500 become connected to the dendrites of the 9 somas in the modeled cortical sheet. This means that the density of stable connected synapses is approximately 0.015 synapses per μm^2. This is also the number that is shown in Figure 3b, which is about 60 synapses stabilized per cell. This density is much easier to compare to experimental data, and below we provide some numbers from literature we already cited in the manuscript as well as a recent preprint.
In the developing cortex:
Leighton, Cheyne and Lohmann 2023 https://doi.org/10.1101/2023.03.02.530772 find up to 0.4 synapses per μm in pyramidal neurons in vivo in the developing mouse visual cortex at P8 to P13. This is almost identical to our value of 0.4 synapses per μm.
Ultanir et al., 2007 https://doi.org/10.1073/pnas.0704031104 find 0.7 to 1.7 spines per μm in pyramidal neurons in vivo in L2/3 of the developing mouse cortex, at P10 to P20.
Glynn et al., 2011 https://doi.org/10.1038/nn.2764 find 0.1 to 0.7 spines per μm^2 in pyramidal neurons in vivo and in vitro in L2/3 of the developing mouse cortex, at P8 to P60.
In the developing hippocampus:
Although these values vary somewhat across experiments, in most cases they are in agreement with our chosen values, especially when taking into account that we are modeling development (rather than adulthood).
- Soma/neuron density: Indeed, we did not exactly mention this number anywhere in the paper. But from the figures we can infer 9 somas growing dendrites on an area of ~34,000 μm^2. Thus, neuron density would be 300 neurons per mm^2. This number seems a bit low after a short search through the literature. For e.g. Keller et al., 2018 https://www.frontiersin.org/articles/10.3389/fnana.2018.00083/full reports about 90,000 neurons per mm^3, albeit in adulthood.
We are also performing a sensitivity analysis where some of these parameters are varied and will include this in the revised manuscript. In particular:
(1) We will vary the nature of the input correlations. In the current model, the synapses in each correlated group receive spike trains with a perfect correlation and there are no correlations across the groups. We will reduce the correlations within group and add non-zero correlations across the groups.
(2) We will vary the density of the neuronal somas. We expect that higher densities of somas will either yield smaller dendritic areas because the different neurons compete more or result in a state where nearby neurons have to complement each other regarding their activity preferences.
(3) We will introduce dynamics in the potential synapses to model the dynamics of axons. We plan to explore several scenarios. We could introduce a gradual increase in the density of potential synapses and implement a cap on the number of synapses that can be alive at the same time, and vary that cap. We could also introduce a lifetime of each synapse (following for example a lognormal distribution). A potential synapse can disappear if it does not form a stable synapse in its lifetime, in which case it could move to a different location.
Point 1.2. Many potentially important phenomena seem to be excluded. I realize that no model can be complete, but the choice of which phenomena to include or exclude from this model could bias studies that make use of it and is worth serious discussion. The development of axons is concurrent with dendrite outgrowth, is highly dynamic, and perhaps better understood mechanistically. In this model, the inputs are essentially static. Growing dendrites acquire and lose growth cones that are associated with rapid extension, but these do not seem to be modeled. Postsynaptic firing does not appear to be modeled, which may be critical to activity-dependent plasticity. For example, changes in firing are a potential explanation for the global changes in dendritic pruning that occur following the outgrowth phase.
As the reviewer concludes, no model can be complete. In agreement with this, here we would like to quote a paragraph from a very nice paper by Larry Abbott (“Theoretical Neuroscience Rising, Neuron 2008 https://www.sciencedirect.com/science/article/pii/S0896627308008921) which although published more than 10 years ago, still applies today:
“Identifying the minimum set of features needed to account for a particular phenomenon and describing these accurately enough to do the job is a key component of model building. Anything more than this minimum set makes the model harder to understand and more difficult to evaluate. The term ‘‘realistic’’ model is a sociological rather than a scientific term. The truly realistic model is as impossible and useless a concept as Borges’ ‘‘map of the empire that was of the same scale as the empire and that coincided with it point for point’’ (Borges, 1975). […] The art of modeling lies in deciding what this subset should be and how it should be described.”
We have clearly stated in the Introduction (e.g. lines 37-75) which phenomena we include in the model and why. The Discussion also compares our model to others (lines 315-373), pointing out that most models either focus on activity-independent or activity-dependent phases. We include both, combining literature on molecular gradients and growth factors, with activity-dependent connectivity refinements instructed by spontaneous activity. We could not think of a more tractable, more minimalist model that would include both activity-independent or activity-dependent aspects. Therefore, we feel that the current manuscript provides sufficient motivation but also a discussion of limitations of the current model.
Regarding including the concurrent development of axons, we agree this is very interesting and currently not addressed in the model. As noted at the bottom of our reply to point 1.1, bullet (3) we are now revising the manuscript to include a simplified form of axonal dynamics by allowing changes in the lifetime and location of potential synapses, which come from axons of presynaptic partners.
Regarding postsynaptic firing, this is indeed super relevant and an important point to consider. In one of our recent publications (Kirchner and Gjorgjieva, 2021 https://www.nature.com/articles/s41467-021-23557-3), we studied only an activity-dependent model for the organization of synaptic inputs on non-growing dendrites which have a fixed length. There, we considered the effect of postsynaptic firing and demonstrated that it plays an important role in establishing a global organization of synapses on the entire dendritic tree of the neuron, and not just local dendritic branches. For example, we showed that could that it could lead to the emergence of retinotopic maps which have been found experimentally (Iacaruso et al., 2017 https://www.nature.com/articles/nature23019). Since we use the same activity-dependent plasticity model in this paper, we expect that the somatic firing will have the same effect on establishing synaptic distributions on the entire dendritic tree. We will make a note of this in the Discussion in the revised paper.
Point 1.3. Line 167. There are many ways to include activity -independent and -dependent components into a model and not every such model shows stability. A key feature seems to be that larger arbors result in reduced growth and/or increased retraction, but this could be achieved in many ways (whether activity dependent or not). It's not clear that this result is due to the combination of activity-dependent and independent components in the model, or conceptually why that should be the case.
We never argued for model uniqueness. There are always going to be many different models (at different spatial and temporal scales, at different levels of abstraction). We can never study all of them and like any modeling study in systems neuroscience we have chosen one model approach and investigated this approach. We do compare the current model to others in the Discussion. If the reviewers have a specific implementation that we should compare our model to as an alternative, we could try, but not if this means doing a completely separate project.
Point 1.4. Line 183. The explanation of overshoot in terms of the different timescales of synaptic additions versus activity-dependent retractions was not something I had previously encountered and is an interesting proposal. Have these timescales been measured experimentally? To what extent is this a result of fine-tuning of simulation parameters?
We found that varying the amount of BDNF controls the timescale of the activity-dependent plasticity (see our Figure 5c). Hence, changing the balance between synaptic additions vs. retractions is already explored in Figure 5e and f. Here we show that the overshoot and retraction does not have to be fine-tuned but may be abolished if there is too much activity-dependent plasticity.
Regarding the relative timescales of synaptic additions vs. retractions: since the first is mainly due to activity-independent factors, and the second due to activity-dependent plasticity, the questions is really about the timescales of the latter two. As we write in the Introduction (lines 60-62), manipulating activity-dependent synaptic transmission has been found to not affect morphology but rather the density and specificity of synaptic connections (Ultanir et al. 2007 https://doi.org/10.1073/pnas.0704031104), supporting the sequential model we have (although we do not impose the sequence, as both activity-independent and activity-dependent mechanisms are always “on”; but note that activity-dependent plasticity can only operate on synapses that have already formed).
Point 1.5. Line 203. This result seems at odds with results that show only a very weak bias in the tuning distribution of inputs to strongly tuned cortical neurons (e.g. work by Arthur Konnerth's group). This discrepancy should be discussed.
First, we note that the correlated activity experienced by our modeled synapses (and resulting synaptic organization) does not necessarily correspond to visual orientation, or any stimulus feature, for that matter.
Nonetheless, this is a very interesting question and there is some variability in what the experimental data show. Many studies have shown that synapses on dendrites are organized into functional synaptic clusters: across brain regions, developmental ages and diverse species from rodent to primate (Kleindienst et al. 2011; Takahashi et al. 2012; Winnubst et al. 2015; Gökçe et al., 2016; Wilson et al. 2016; Iacaruso et al., 2017; Scholl et al., 2017; Niculescu et al. 2018; Kerlin et al. 2019; Ju et al. 2020). Interestingly, some in vivo studies have reported lack of fine-scale synaptic organization (Varga et al. 2011; X. Chen et al. 2011; T.-W. Chen et al. 2013; Jia et al. 2010; Jia et al. 2014), while others reported clustering for different stimulus features in different species. For example, dendritic branches in the ferret visual cortex exhibit local clustering of orientation selectivity but do not exhibit global organization of inputs according to spatial location and receptive field properties (Wilson et al. 2016; Scholl et al., 2017). In contrast, synaptic inputs in mouse visual cortex do not cluster locally by orientation, but only by receptive field overlap, and exhibit a global retinotopic organization along the proximal-distal axis (Iacaruso et al., 2017). We proposed a theoretical framework to reconcile these data: combining activity-dependent plasticity similar to the BDNF-proBDNF model that we used in the current work, and a receptive field model for the different species (Kirchner and Gjorgjieva, 2021 https://www.nature.com/articles/s41467-021-23557-3). We can mention this aspect in the revised manuscript.
Point 1.6. Line 268. How does the large variability in the size of the simulated arbors relate to the relatively consistent size of arbors of cortical cells of a given cell type? This variability suggests to me that these simulations could be sensitive to small changes in parameters (e.g. to the density or layout of presynapses).
As noted at the bottom of our reply to point 1.1, bullet (3) we are now revising the manuscript to include changes in the lifetime and location of potential synapses.
Point 1.7. The modeling of dendrites as two-dimensional will likely limit the usefulness of this model. Many phenomena- such as diffusion, random walks, topological properties, etc - fundamentally differ between two and three dimensions.
The reviewer is right about there being differences between two and three dimensions. But a simpler model does not mean a useless model even if not completely realistic. We have ongoing work that extends the current model to 3D but is beyond the scope of the current paper. In systems neuroscience, people have found very interesting results making such simplified geometric assumptions about networks, for instance the one-dimensional ring model has been used to uncover fundamental insights about computations even though highly simplified and abstracted.
Point 1.8. The description of wiring lengths as 'approximately optimal' in this text is problematic. The plotted data show that the wiring lengths are several deviations away from optimal, and the random model is not a valid instantiation of the 2D non-overlapping constraints the authors imposed. A more appropriate null should be considered.
We did not use the term “optimal” in line with previous literature. We wrongly referred to the minimal wiring length as the optimal wiring length, but neurons can optimize their wiring not only by minimizing their dendritic length (e.g. work of Hermann Cuntz). In the revised manuscript, we will replace the term “optimal wiring” with “minimal wiring”. Then we will compare the wiring length in the model with the theoretically minimal wiring length, the random wiring length and the actual data.
Point 1.9. It's not clear to me what the authors are trying to convey by repeatedly labeling this model as 'mechanistic'. The mechanisms implemented in the model are inspired by biological phenomena, but the implementations have little resemblance to the underlying biophysical mechanisms. Overall my impression is that this is a phenomenological model intended to show under what conditions particular patterns are possible. Line 363, describing another model as computational but not mechanistic, was especially unclear to me in this context.
What we mean by mechanistic is that we implement equations that model specific mechanisms i.e. we have a set of equations that implement the activity-independent attraction to potential synapses (with parameters such as the density of synapses, their spatial influence, etc) and the activity-dependent refinement of synapses (with parameters such as the ratio of BDNF and proBDNF to induce potentiation vs depression, the activity-dependent conversion of one factor to the other, etc). This is a bottom-up approach where we combine multiple elements together to get to neuronal growth and synaptic organization. This approach is in stark contrast to the so-called top-down or normative approaches where the method would involve defining an objective function (e.g. minimal dendritic length) which depends on a set of parameters and then applying a gradient descent or other mathematical optimization technique to get at the parameters that optimize the objective function. This latter approach we would not call mechanistic because it involves an abstract objective function (who could say what a neuron or a circuit should be trying to optimize) and a mathematical technique for how to optimize the function (we don’t know of neurons can compute gradients of abstract objective functions).
Hence our model is mechanistic, but it does operate at a particular level of abstraction/simplification. We don’t model individual ion channels, or biophysics of synaptic plasticity (opening and closing of NMDA channels, accumulation of proteins at synapses, protein synthesis). We do, however, provide a biophysical implementation of the plasticity mechanism though the BDNF/proBDNF model which is more than most models of plasticity achieve, because they typically model a phenomenological STDP or Hebbian rule that just uses activity patterns to potential or depress synaptic weights, disregarding how it could be implemented.
Reviewer #2 (Public Review):
This work combines a model of two-dimensional dendritic growth with attraction and stabilisation by synaptic activity. The authors find that constraining growth models with competition for synaptic inputs produces artificial dendrites that match some key features of real neurons both over development and in terms of final structure. In particular, incorporating distance-dependent competition between synapses of the same dendrite naturally produces distinct phases of dendritic growth (overshoot, pruning, and stabilisation) that are observed biologically and leads to local synaptic organisation with functional relevance. The approach is elegant and well-explained, but makes some significant modelling assumptions that might impact the biological relevance of the results.
Strengths:
The main strength of the work is the general concept of combining morphological models of growth with synaptic plasticity and stabilisation. This is an interesting way to bridge two distinct areas of neuroscience in a manner that leads to findings that could be significant for both. The modelling of both dendritic growth and distance-dependent synaptic competition is carefully done, constrained by reasonable biological mechanisms, and well-described in the text. The paper also links its findings, for example in terms of phases of dendritic growth or final morphological structure, to known data well.
Weaknesses:
The major weaknesses of the paper are the simplifying modelling assumptions that are likely to have an impact on the results. These assumptions are not discussed in enough detail in the current version of the paper.
- Axonal dynamics.
A major, and lightly acknowledged, assumption of this paper is that potential synapses, which must come from axons, are fixed in space. This is not realistic for many neural systems, as multiple undifferentiated neurites typically grow from the soma before an axon is specified (Polleux & Snider, 2010). Further, axons are also dynamic structures in early development and, at least in some systems, undergo activity-dependent morphological changes too (O'Leary, 1987; Hall 2000). This paper does not consider the implications of joint pre- and post-synaptic growth and stabilisation.
We thank the reviewer for the summary of the strengths and weaknesses of the work. While we feel that including a full model of axonal dynamics is beyond the scope of the current manuscript, some aspects of axonal dynamics can be included. In a revised model, we will introduce a gradual increase in the density of potential synapses and implement a cap on the number of synapses that can be alive at the same time, and vary that cap. We plan to also introduce a lifetime of each synapse (following for example a lognormal distribution). A potential synapse can disappear if it does not form a stable synapse in its lifetime, in which case it could move to a different location. See also our reply to reviewer comment 1.1, bullet (3).
- Activity correlations
On a related note, the synapses in the manuscript display correlated activity, but there is no relationship between the distance between synapses and their correlation. In reality, nearby synapses are far more likely to share the same axon and so display correlated activity. If the input activity is spatially correlated and synaptic plasticity displays distance-dependent competition in the dendrites, there is likely to be a non-trivial interaction between these two features with a major impact on the organisation of synaptic contacts onto each neuron.
We are exploring the amount of correlation (between and within correlated groups) to include in the revised manuscript (see also our reply to reviewer comment 1.1, bullet (1)).
However, previous experimental work, (Kleindienst et al., 2011 https://doi.org/10.1016/j.neuron.2011.10.015) has provided anatomical and functional analyses that it is unlikely that the functional synaptic clustering on dendritic branches is the result of individual axons making more than one synapse (see pg. 1019).
- BDNF dynamics
The models are quite sensitive to the ratio of BDNF to proBDNF (eg Figure 5c). This ratio is also activity-dependent as synaptic activation converts proBDNF into BDNF. The models assume a fixed ratio that is not affected by synaptic activity. There should at least be more justification for this assumption, as there is likely to be a positive feedback relationship between levels of BDNF and synaptic activation.
The reviewer is correct. We used the BDNF-proBDNF model for synaptic plasticity based on our previous work: Kirchner and Gjorgjieva, 2021 https://www.nature.com/articles/s41467-021-23557-3.
There, we explored only the emergence of functionally clustered synapses on static dendrites which do not grow. In the Methods section (Parameters and data fitting) we justify the choice of the ratio of BDNF to proBDNF from published experimental work. We also performed sensitivity analysis (Supplementary Fig. 1) and perturbation simulations (Supplementary Fig. 3), which showed that the ratio is crucial in regulating the overall amount of potentiation and depression of synaptic efficacy, and therefore has a strong impact on the emergence and maintenance of synaptic organization. Since we already performed all this analysis, we do not expect there will be any differences in the current model which includes dendritic growth, as the activity-dependent mechanism has such a different timescale.
A further weakness is in the discussion of how the final morphologies conform to principles of optimal wiring, which is quite imprecise. 'Optimal wiring' in the sense of dendrites and axons (Cajal, 1895; Chklovskii, 2004; Cuntz et al, 2007, Budd et al, 2010) is not usually synonymous with 'shortest wiring' as implied here. Instead, there is assumed to be a balance between minimising total dendritic length and minimising the tree distance (ie Figure 4c here) between synapses and the site of input integration, typically the soma. The level of this balance gives the deviation from the theoretical minimum length as direct paths to synapses typically require longer dendrites. In the model this is generated by the guidance of dendritic growth directly towards the synaptic targets. The interpretation of the deviation in this results section discussing optimal wiring, with hampered diffusion of signalling molecules, does not seem to be correct.
We agree with this comment. We had wrongly used the term “optimal wiring” as neurons can optimize their wiring not only by minimizing their dendritic length but other factors as noted by the reviewer. In the revised manuscript will replace the term “optimal wiring” with “minimal wiring” and discuss these differences to previous work.
Reviewer #3 (Public Review):
The authors propose a mechanistic model of how the interplay between activity-independent growth and an activity-dependent synaptic strengthening/weaken model influences the dendrite shape, complexity and distribution of synapses. The authors focus on a model for stellate cells, which have multiple dendrites emerging from a soma. The activity independent component is provided by a random pool of presynaptic sites that represent potential synapses and that release a diffusible signal that promotes dendritic growth. Then a spontaneous activity pattern with some correlation structure is imposed at those presynaptic sites. The strength of these synapses follow a learning rule previously proposed by the lab: synapses strengthen when there is correlated firing across multiple sites, and synapses weaken if there is uncorrelated firing with the relative strength of these processes controlled by available levels of BDNF/proBDNF. Once a synapse is weakened below a threshold, the dendrite branch at that site retracts and loses its sensitivity to the growth signal
The authors run the simulation and map out how dendrites and synapses evolve and stabilize. They show that dendritic trees growing rapidly and then stabilize by balancing growth and retraction (Figure 2). They also that there is an initial bout of synaptogenesis followed by loss of synapses, reflecting the longer amount of time it takes to weaken a synapse (Figure 3). They analyze how this evolution of dendrites and synapses depends on the correlated firing of synapses (i.e. defined as being in the same "activity group"). They show that in the stabilized phase, synapses that remain connected to a given dendritic branch are likely to be from same activity group (Figure 4). The authors systemically alter the learning rule by changing the available concentration of BDNF, which alters the relative amount of synaptic strengthening, which in turn affects stabilization, density of synapses and interestingly how selective for an activity group one dendrite is (Figure 5). In addition the authors look at how altering the activity-independent factors influences outgrowth (Figure 6). Finally, one of the interesting outcomes is that the resulting dendritic trees represent "optimal wiring" solutions in the sense that dendrites use the shortest distance given the distribution of synapses. They compare this distribute to one published data to see how the model compared to what has been observed experimentally.
There are many strengths to this study. The consequence of adding the activity-dependent contribution to models of synapto- and dendritogenesis is novel. There is some exploration of parameters space with the motivation of keeping the parameters as well as the generated outcomes close to anatomical data of real dendrites. The paper is also scholarly in its comparison of this approach to previous generative models. This work represented an important advance to our understanding of how learning rules can contribute to dendrite morphogenesis
We thank the reviewer for the positive evaluation of the work and the suggestions below.




