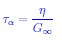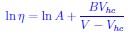Free volume theory explains the unusual behavior of viscosity in a non-confluent tissue during morphogenesis

Reviewer #1 (Public Review):

The authors consider data by the Heisenberg group on rheological properties of non-confluent tissue in zebrafish embryos. These data had shown a steep increase and subsequent saturation in viscosity with cell density. The authors introduce a physical agent-based model of such tissues that accounts for the dispersion in cell size and the softness of the cells. The model is inspired by previous models to study glassy dynamics and reveals essential physical features that can explain the observed behavior. It goes beyond previous studies that had analysed the observations in terms of a percolation problem. The numerics is thoroughly done and could have a deep impact on how we describe non-confluent tissues.

Reviewer #2 (Public Review):

This paper explores how minimal active matter simulations can model tissue rheology, with applications to the in vivo situation of zebrafish morphogenesis. The authors explore the idea of active noise, particle softness and size heterogeneity cooperating to give rise to surprising features of experimental tissue rheologies (in particular an increase and then a plateau in viscosity with fluid fraction). In general, the paper is interesting from a theoretical standpoint, by providing a bridge between concepts from jamming of particulate systems and experiments in developmental biology. The idea of exploring a free space picture in this context is also interesting. However, I'm still unsure right now though of how much it can be applied to the specific system that the authors refer to - which could be fixed either by doing theoretical checks or considering other experimental systems/models reported in the recent literature.

Reviewer #3 (Public Review):

The authors successfully explain the sharp rise and subsequent saturation of the viscosity in dependence of cell packing fraction in zebrafish blastoderm with the help of a 2D model of soft deformable, polydisperse and self-propelled (active) disks. The main experimental observations can be reproduced and the unusual dependence of the viscosity on packing fraction can be explained by the available free area and the emergent motility of small sized cells facilitating multi-cell rearrangement in a highly jammed environment.

The paper is very well written, the results (experimental as well as theoretical) are original and scientifically valid. This is an important contribution to understanding the rheological properties of non-confluent tissues linking equilibrium and transport properties.

Author Response

The following is the authors’ response to the original reviews.

Reviewer #1

As written in my public review I consider the science of this work to be high quality. I have some suggestions for the write-up though. As a general comment, I think that too much has been put into the appendices. In particular, the main text could contain more details about the model.

We are pleased that this Reviewer feels that our work to be of “high quality”. We value the reviewer’s insightful suggestions and comments. Following this Reviewer’s suggestion we have moved certain sections to the main text.

In what follows, we provide responses to each of the reviewer’s inquiry, and indicate the appropriate changes in the revised version.

P2 -

ϕ is introduce as packing fraction - on p3 it’s called cell density. Also it is not clear whether it is an area fraction or a cell number density. Please define properly and I would suggest sticking to one notion.

ϕ is the cell packing fraction. In two dimensions (as is the case in our simulations) it is the area fraction. However, in order to stick to one general notation (independent of dimension) we use “packing fraction” to represent how densely the cells are packed. We changed it the revised manuscript to ensure uniformity.

P3 -

“which should and should slow down the overall dynamics” Typo?

Corrected it in the revised manuscript.

“One would intuitively expect that the ϕfree should decrease with increasing cell density” Please, define ϕfree

ϕfree is defined in Eqn. 4. We ought to have defined it in the introduction.

“When ϕ exceeds ϕS, the free area ϕfree saturates because the soft cells interpenetrate each other,” I suggest clearly distinguishing between biological cells and the agents (disks) used in the simulation. Please, also clarify What interpenetration of agents corresponds to in tissues?

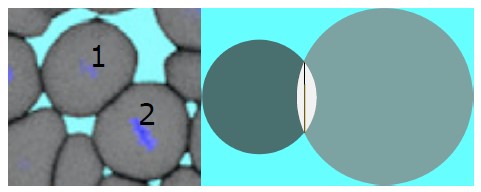
We have rewritten the sentence as, ”The simulations show that when..” Soft disks used in the simulations seem to be not an unrealistic model for biological cells. The small deformations noted in our model is not that different from the cells in the tissues. For visual reference, please see Author response image 1. In the left panel of the figure, a 2D snapshot of the experimental zebrafish tissue, displays the deformation of cells labeled as 1 and 2. Likewise, the right panel illustrates the extent to which such deformations are replicated in the simulation by allowing two cells to overlap (the white area in the right panel of Author response image 1 represents the interpenetration). In the revised manuscript, we have made the necessary change from “soft cells” to “soft disks.”

Author response image 1.

Snapshots of zebrafish tissue (left panel) (Ref. [14] main text) and model two dimensional tissue (right). In the right panel the white area represents the overlap and the black vertical line represents the intersection.

“The facilitation mechanism, invoked in glassy systems [22] allows large cells to move with low mobility.” What is the facilitation mechanism?

Facilitation, which is an intuitive idea, that refers to a mechanism by which cells in a in highly jammed environment can only move if the neighboring cells get out of the way. In our case (as shown in the text (Fig.3 (A) and Fig. 13 (A) & (B)) the smaller cells move faster almost independent of ϕ. When a small cell moves, it creates a void which could facilitate neighboring cells (including big ones) to move.

“η (or relaxation time)” I suggest explaining the link between η and the relaxation time.

First, in making this point on aging we only showed that the relaxation time is independent of the waiting time. In the revised manuscript we deleted η.

Although not germane to this study, in the literature on glass transition, it is not uncommon to use relaxation time τα (as a proxy of viscosity η) to describe the dynamics. The relation between τα and η is given by

where G∞ is the “infinite frequency” shear modulus, which holds in unjammed or in liquids. This relation suggests that τα is proportional to η, which is almost never satisfied in glass forming systems.

P5 - “In addition, the elastic forces characterizing cell-cell interactions are soft, which implies that the cells can penetrate with rij − (Ri + Rj) < 0 when they are jammed.” Is this about the model or the biological tissue? Presumably the former, because real cells do not penetrate each other, right? What are rij, Ri and Rj?

This is about the model. The cells are sufficiently soft that they can be deformed, which allows for modest interpenetration. Real cells exhibit similar behavior (see Fig. 1). In inset of Fig. 4 (b) rij is the center to center distance between cells with radii Ri and Rj. It is better to use the word overlap instead of penetrate, which is what we have done in the revised version.

“we simulated a highly polydisperse system (PDs) in which the cell sizes vary by a factor of ∼ 8” Is it important to have a factor 8 - the zebra fish tissue presents a factor 5 − 6?

This is an important question, which is difficult to answer using analytic theory. It does require simulations unfortunately. We do not know a priori the polysipersity value needed to observe saturation in η at high value of ϕ. However, we have shown that the a system with one type of cell (monodisperse) crystallizes. Furthermore, mixtures of two cell types do not show any saturation in η over the parameter range that we explored. A systematic simulation study is needed to explore a range of parameter values to determine the minimum PD, which would match the experimental findings.

We performed 3D simulations to figure out if much less PD would yield saturation in η. Preliminary simulations in three dimensions with a lower value of PD (11.5% with a size variations by a factor of ≈ 2 ) exhibits saturation in the relaxation time. For comparison, the value of PD in the current work is ≈ 24% with a size variation by a factor of 8.

P6 -

“which is related to the Doolittle equation [26] for fluidity ( )” what is the Doolittle equation? Is it important here? Also: “VFT equation for cells”? Is it the same as given on p.2 - so nothing special for cells - or a different one?

Historically, the Doolittle equation was proposed to describe the change in η in terms of free volume in the context polymer systems over 60 years ago. The physics in the polymers is very different from the soft models for cells considered here. Nevertheless, the equations has meaning in the context as well. The Doolittle (other names associated with similar equations are Ferry, Flory... ) equation is given by

, where A and B are constants, V is the total volume and Vhc is the hardcore volume. Essentially, is the relative free volume. It can be shown that one can arrive at the VFT equation starting from the Doolittle equation.

The VFT equation for cells is same as given in page 2, which we restate for completeness. Here, we introduce the apparent activation energy.

“The stress-stress tensor” Why not simply stress tensor?

We have corrected it.

“shows qualitatively the same behavior as the estimate of viscosity (using dimensional arguments) made in experiments.” Where is this shown?

The dependence of viscosity as a function ϕ is shown in Figure 1 (c).

P7 -

Fig 2A caption “dashed line” Maybe full line?

This should be full line. It is fixed in in the revised manuscript.

P8 -

“a puzzling finding that is also reflected” Why is it puzzling?

In figure 2 (C), it shows that the increase in the duration in the plateau of Fs(q,t) ceases when ϕ exceeds ≈ 0.90. This to us is puzzling (always a matter of perspective) because we expected that the duration of Fs(q,t) plateau to increase as a function of ϕ based on the VFT behavior for ϕ ≤ ϕS. As a result, we imagined that the relaxation time τα would continue to increase beyond ϕS. However, the simulations show that the relaxation time is essentially a constant for ϕ > 0.90, which implies that the soft disk system (our model for the tissue) is an unusual with behavior that has no counter part in the material world.

“If the VFT relation continues” –“If the VFT relation continued”

We have fixed it.

First paragraph does not seem to be coherent

What is RS (or Rs)?

RS is the radius of the small cell. In the revised manuscript we have made this clear.

P10 -

Please, define the waiting time.

The waiting time refers to the period between sample preparation and data collection either in experiments or in simulations. In an ergodic system, the properties should not depend on the waiting time provided provided it is large. In other words, after the system reaches thermal equilibrium, the waiting time tω should not have an impact on the properties of the system.

“fully jammed” Please, define.

The term “fully jammed” refers to a state in which the constituent particles in a system do not move. For example, it a hard sphere system at a packing fraction of approximately 0.84 is fully jammed, which implies there is wiggle room for a particle move without violating the excluded volume restriction. At this specific packing fraction, the hard sphere system undergoes a jamming transition, resulting in the particles becoming completely immobile. The nonconfluent tissue modeled here is not fully jammed.

P11 -

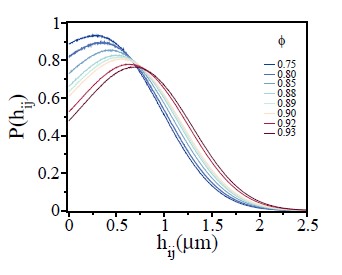
Fig.4 it is hard to see that the width of P(hij) increases with ϕ.

Please see Author response image 2 with a less number of curves for a better visualization. We have replaced this figure in the revised version.

Author response image 2.

Probability of overlap (hij) between two cells, P(hij), for various ϕ values.

“Thus, even if the cells are highly jammed at ϕ ≈ ϕS, free area is available because of an increase in the overlap between cells.” This conclusion seems premature at this point.

The Referee is correct. This is shown in Fig. 5. We amended the ends of the sentence to reflect this observation.

P12 -

“as is the case when the extent of compression increases” extent of compression = density?

This is correct. Extent of compression corresponds to the packing fraction or the density.

“This effect is expected to occur with high probability at ϕS and beyond,” Why? What is special about ϕS.

To achieve high packing fractions beyond a certain value of ϕ soft cells have, which would occur at a certain value ϕS. In the system studied here, ϕ ≈ 0.90 = ϕS. Note that ϕS could be altered by changing the system parameters.

P15 -

“local equilibrium” In a thermodynamic sense? There is also cell migration, so thermodynamic equilibrium does not seem to be appropriate.

This is an important point. The observation that equilibrium concepts hold in what is manifestly a non-equilibrium system is a surprise. It is referred in a thermodynamic sense. We agree with the reviewer because of cell division (in Ref. [14] main text), cell death, thermodynamic equilibrium does not seems to be appropriate. This is exactly the point we raise in the introduction. However, considering the timescale of cell division and death it appears that there may be a local steady state, which we we call a “local equilibrium”. As a consequence phase transition ideas and Green-Kubo relations are applicable. Indeed, a surprise in the conclusion in Ref. [14] is that in the zebrafish morphogenesis equilibrium description seems adequate.

“number of near neighbor cells that is in contact with the ith cell. The jth cell is the nearest neighbor of the ith cell, if hij > 0” A neighbour cell or the nearest neihbor?

A neighbour cell is accurate.

P16 -

“In our model there is no dynamics with only systematic forces because the temperature is zero.” What is a systematic force? I do not understand the sentence.

Systematic force between two cells is defined in Eqn. 5 in the main text. Because temperature is not a relevant variable in our model, we want to emphasize that in the absence of self propulsion, the cells would not move at all.

Reviewer #2

Major comments:

A/ Role of size polydispersity

In the text, and also in the methods (Appendix A), the authors mention that they need large polydispersity of particle sizes to explain the viscous plateau, as the dynamics of small vs large cells are ”dramatically different” (Appendix G). They simulate a system where cell sizes vary by a factor 8, mentioning this is typical in tissues, but I found this quite surprising - this would be heterogeneities in cell volume of 500, many orders of magnitude above what has been measured in tissues. As far as I’m aware, divisions are quite symmetric and synchronous in early vertebrate embryogenesis, so volume variations are expected to be very small (similarly in epithelial tissues, where jamming has been looked at extensively, I’m not aware of examples with ratio of 8 between cell diameters). One question I had is that when the authors look at ”small polydispersity”, there are 50 − 50 mixtures. Would small polydispersity with continuous distributions change this picture? Could they take their current simulations but smoothly change the ratio of polydispersity from 8 to 0 to see exactly how much they need to explain viscosity plateauing, and at which point is the transition?

We thank the reviewer for raising this important question, which was also a concern for Reviewer #1. The value of polydispersity (PD) required to observe such behavior is not known a priori even within the simple model used. We selected a PD value, with a size variation of a factor of 8, guided in part by the experiment (projection onto 2D) shown in Figure 1(B) and Figure 6(D). We also showed that the monodisperse system crystallizes, and the binary system do not show signs of saturation within the explored range of parameter space and ϕ. This suggests that a certain degree of size dispersity is necessary to obtain saturation in η.

As discussed in Appendix B, the binary system is characterized by the variables , where RB and RS represent the radii of the big and small cells, respectively, and the packing fraction ϕ. By more fully exploring the parameter space encompassing λ and ϕ than we did, it maybe possible, as the Referee suggests, that a system with two different cell sizes would yield the experimentally observed dependence of η on ϕ.

As part of an answer to the Reviewer #1 on a the same issue, we mentioned results of preliminary simulations in three dimensions with reduced levels of polydispersity, and discovered that at lower levels of polydispersity (variation in size by a factor of ≈ 2 and polydispersity value 11.50%), the relaxation time does saturate beyond a certain packing fraction (see Fig. 3). We have not established if η, the key quantity of interest, would exhibit a similar behavior in 3D.

Author response image 3.

(A) τα as a function of ϕ for 11% polydispersity with size variation by a factor of ∼ 2 in the three dimensional system. (B) Same as (A) except polydispersity value is 24% and a size variation by a factor of ∼ 8.

B/ Role of fluctuations/self-propulsion in this system, and relationship to recent findings

“A priori it is unclear why equilibrium concepts should hold in zebrafish morphogenesis, which one would expect is controlled by non-equilibrium processes such as self-propulsion, growth and cell division. ”

This is raised as a key paradox, but is not very clear to me in the context raised by the authors. In particular, they use self-propulsion as a source of activity and explain the evolution of viscosity but a facilitation process involving re-arrangements/motility. But I don’t think self-propulsion has been argued to play a role in zebrafish blastoderm - Ref 14 argues that this is effectively a zerotemperature phenomenon and that cell motility/rearrangements do not show any correlation with viscosity. So this part of the model assumption was not clear to me in relationship with the proposed experimental system. Active noise has been proposed to play key roles in other systems, including motility-driven and tension fluctuation-driven unjamming (among many others Bi et al, PRX, 2016, Mitchel et al, Nat Comm, 2020, Pinheiro et al, Nat Phys, 2022 as well as Kim & Campas, Nat Physics, 2021) - maybe this is somewhere where the author model could fit? In Kim & Campas, Nat Phys, 2021 in particular, the authors develop simulations of non-confluent tissues with noise, that seems to bear some resemblance to the model developed here, so it would be important to discuss the similarities and distinctions (usually I think polydispersity is not considered indeed). In general, the authors look here at a particle based model, but cells have adhesions with well-defined contact angles, so there is a question of the cross-over between their findings and the large body of recent literature on active foams/vertex models (which are not really discussed there).

We appreciate the lengthy comment here, and there is a lot to unpack. We also thank the referee for the references, some of which we did not know about earlier.

The primary objective of our study is to determine the simplest minimal model that would explain the experimentally observed dependence of viscosity in zebrafish blastoderm tissue as ϕ is increased beyond a certain packing fraction during morphogenesis. In Reference 14, the authors analyzed the data using the framework of rigidity percolation theory and presented evidence of a genuine equilibrium phase transition. Consequently, one would that expect zebrafish blastoderm tissue to be in equilibrium, which is surprising from many perspectives. However, since the tissue is a growing system involving numerous cell divisions and cell death, it is not immediately evident whether the assumption of equilibrium is valid. Indeed, the same problem arises when considering the glass transition where rapid cooling drives the system out of equilibrium. Nevertheless, heat capacity and η are often analyzed using the notion of equilibrium. Hence, considering this issue within the context of our research appears to be reasonable.

To the best of our knowledge, the authors in Ref. 14 did not provide an explanation for the η behavior. The focus was, which was excellent and is the basis on which we initiated this study, was on the use of rigidity percolation theory to explain the results. Indeed, they performed an experiment by mildly reducing myosin II activity, which apparently affects cell motility. The quantitative effect was not reported.

We did not impose any requirement of cell rearrangements etc in the model. There is essentially one variable, free area available, that explains the η dependence on ϕ. It is possible that one can come up with other zero temperature models that could also explain the data. To the best of our knowledge, it has not been proposed.

It would be interesting to set our model in the context of other models that the referee points out. This would be an interesting research topic to explore. The only comment we would like to make is that it is unclear how vertex model for confluent tissues could explain the viscosity data.

C/ Calculation of the effective shear viscosity

The authors calculate viscosity from a Green-Kubo relation, although it would be good to clarify at which time scale (and maybe even shear amplitude) they expect this to be valid. These kinds of model would be expected to show plastic rearrangements for large deformations for instance, could the authors simulate realistic rheological deformations (e.g. Kim & Campas, 2021 applying external shear on the simulations) to see how much this matches both their expectation and the data?

Once it is established that there is local equilibrium (as implied by the use of phase transition ideas to analyse the experimental data in Ref. 14), it is natural to use the Green-Kubo relation to calculate transport properties. Hence, for our purposes, it is valid for all time scales and amplitude. The Reviewer also wonders if the model could be used to simulate response to shear in order to probe rheological properties. There is no conceptual issue here and indeed this is an excellent suggestion that we intend to pursue in the future.

D/ Role of cell adhesion

The authors consider soft elastic disks of different sizes but unless I missed it, there is no adhesion being considered. This is expected to play a key role in jamming and multicellular mechanics, so I think the authors should either look at what this changes in their simulations, or at least discuss why they are neglecting it. One reason I’m asking is that it’s not totally clear to me that the ”free space” picture, coming from the fact that cells can interpenetrate in their model would hold in a model of deformable cells adhering to each other with constant volume (leading to more equilibration of deformations it would seem?).

The referee raises another question regarding the lack of adhesion in the simulations. As pointed out before, we were trying to create a minimal model to account for the experimental observations for η upon changing the packing fraction. Thus, we a coarse-grained model where we considered poly-disperse cells with elastic interactions which recapitulates the experimental observations. The referee is correct that adhesion plays a role in jammed systems, and examination of how it would affect is an aspect that would be interesting to consider in the future. We hasten to add that even systems without attractive adhesion-type interaction become jammed. In principle, in many-body systems, the parameter space is large and one needs to carefully determine which parameter is important for the problem at hand. Therefore, in the first pass we did not find the need to consider the role of adhesion.

Minor comments:

The writing could be condensed in some places, with some details being moved to SI (for instance, section E on ageing is very short and seem more suited for supplements, or at least not as an independent section, note that the figure numbering also jumps to Fig. 9 there, although it’s Fig. 3 just before and Fig. 9 just after - re-ordering into main and supporting figures would be clearer.

We thank the Reviewer for this recommendation. The ageing section, although is short, it does provide a line of evidence that equilibrium approaches could be valid. We have modestly expanded the section by moving Appendix D to the main text, a general suggestion made by Referee 1. We have tried to be consistent in the numbering of figures in the revision.

Reviewer #3

I am very much in favor of the manuscript in its present form - I only suggest commenting (in the manuscript) on the issue described below.

Motivated by the fact that the experimental system consists of living, motile cells the authors use an active particle model (eq. 6) with stochastic selfpropulsion as the only source for noise (zero-temperature). It would be useful to elaborate briefly how important this stochastic self-propulsion is for the emergent rheological properties of the system (as summarized above): would these properties also be present in the “passive” version of the same model at “non-vanishing” temperature, and if not, why? Or analogously in a “passive” version which is “shaken”, reminiscent of shaken granular matter? To clarify these issues would relate this study to (or discriminate it from) passive, but complex, liquids or granular matter.

We appreciate the reviewer’s positive feedback on our work. The reviewer has raised an important question concerning our model in which self-propulsion serves as the source of noise. Without self-propulsion, the system would come to a stationary state after reaching mechanical equilibrium. As mentioned in Eqn. (6) (in the main text), we can define a characteristic time . It is possible that scaling the time t by τ would not alter the results.

The second question raised by the reviewer is also important. A passive version of the model would be to consider Eq. 6 in our article, and instead of using activity use the standard stochastic force. The resulting force would be at a finite temperature,. The coefficient of noise (a diffusion term) would be related to γi through the Fluctuation dissipation theorem(FDT)). Such a system of equations cannot ne mapped to Eq. 6 in which µ and γi are independently varied. It is unlikely that such a model, incorporating a “non-vanishing” temperature, would not result in the observed dependence of η on ϕ for the following reason. The passive model represents a polydisperse system, which would form a glass with η increasing with volume fraction, following the VFT law, as has been demonstrated in the glass transition literature for harmonic glasses. The other proposal whether the shaken version version would explain the experiments is also interesting. These are worth pursuing in future studies.