Modelling collective behavior in groups of mice housed under semi-naturalistic conditions

Reviewer #2 (Public review):

The authors have constructively responded to previous referee comments and I believe that the manuscript is a useful addition to the literature. I particularly appreciate the quantitative approach to social behavior, but have two cautionary comments.

(1) Conceptually it is important to further justify why this particular maximum entropy model is appropriate. Maximum entropy models have been applied across a dizzying array of biological systems, including genes, neurons, the immune system, as well as animal behavior, so would seem quite beneficial to explain the particular benefits here, for mouse social behavior as coarse-grained through the eco-hab chamber occupancy. This would be an excellent chance to amplify what the models can offer for biological understanding, particularly in the realm of social behavior

(2) Maximum entropy models of even intermediate size systems involve a large number of parameters. The authors are transparent about that limitation here, but I still worry that the conclusion of the sufficiency of pairwise interactions is simply not general, and this may also relate to the differences from previous work. If, as the authors suggest in the discussion, this difference is one of a choice of variables, then that point could be emphasized. The suggestion of a follow up study with a smaller number of mice is excellent.

Reviewer #3 (Public review):

Summary:

Chen et al. present a thorough statistical analysis of social interactions, more precisely, co-occupying the same chamber in the Eco-HAB measurement system. They also test the effect of manipulating the prelimbic cortex by using TIMP-1 that inhibits the MMP-9 matrix metalloproteinase. They conclude that altering neural plasticity in the prelimbic cortex does not eliminate social interactions, but it strongly impacts social information transmission.

Strengths:

The quantitative approach to analyzing social interactions is laudable and the study is interesting. It demonstrates that the Eco-HAB can be used for high throughput, standardized and automated tests of the effects of brain manipulations on social structure in large groups of mice.

Weaknesses:

A demonstration of TIMP-1 impairing neural plasticity specifically in the prelimbic cortex of the treated animals would greatly strengthen the biological conclusions. The Eco-HAB provides coarser spatial information compared to some other approaches, which may influence the conclusions.

Author response:

The following is the authors’ response to the original reviews.

We would like to thank the reviewer and the editor for carefully reading our manuscript, and acknowledging the strength of combining quantitative analysis with semi-naturalistic experiments on mice social behavior. Please find below our response to both the public review and the recommendation to the authors. As a summary, we have included additional figures and texts such as

- a new Results subsection “Choosing timescales for analysis ” (page 6)

- a new Materials and Methods subsection “Maximum entropy model with triplet interactions” (page 17)

- new supplementary figures, which have current labels of:

- Figure 2 - figure supplement 5

- Figure 2 - figure supplement 6

- Figure 2 - figure supplement 7

- Figure 4 - figure supplement 1

- Figure 4 - figure supplement 2

Public Reviews:

Reviewer #1 (Public Review):

Summary:

In this manuscript, Chen et al. investigate the statistical structure of social interactions among mice living together in the ECO-Hab. They use maximum entropy models (MEM) from statistical physics that include individual preferences and pair-wise interactions among mice to describe their collective behavior. They also use this model to track the evolution of these preferences and interactions across time and in one group of mice injected with TIMP-1, an enzyme regulating synaptic plasticity. The main result is that they can explain group behavior (the probability of being together in one compartment) by a MEM that only includes pair-wise interactions. Moreover, the impact of TIMP-1 is to increase the variance of the couplings J_ij, the preference for the compartment containing food, as well as the dissatisfaction triplet index (DTI).

Strengths:

The ECO-Hab is a really nice system to ask questions about the sociability of mice and to tease apart sociability from individual preference. Moreover, combining the ECO-Hab with the use of MEM is a powerful and elegant approach that can help statistically characterize complex interactions between groups of mice -- an important question that requires fine quantitative analysis.

Weaknesses:

However, there is a risk in interpreting these models. In my view, several of the comparisons established in the current study would require finer and more in-depth analysis to be able to establish firmer conclusions (see below). Also, the current study, which closely resembles previous work by Shemesh et al., finds a different result but does not provide the same quantitative model comparison included there, nor a conclusive explanation of why their results are different. In total, I felt that some of the results required more solid statistical testing and that some of the conclusions of the paper were not entirely justified. In particular, the results from TIMP-1 require proper interaction tests (group x drug) which I couldn't find. This is particularly important when the control group has a smaller N than the drug groups.

We would like to thank the reviewer and the editor for carefully reading our manuscript, and acknowledging the strength of combining quantitative analysis with semi-naturalistic experiments on mice social behavior. Thanks to the reviewer’s suggestion, we have improved our manuscript by

(1) A proper comparison with Shemesh et al., especially to include maximum entropy models with triplet interactions. We show that triplet models overfit even given the entire 10 day dataset, which limits our study to look at pairwise interactions.

(2) Results on cross-validation for both triplet interaction models and pairwise interaction models, completed on aggregates of various length of days. This analysis showed that pairwise models overfit for single-day data, and led us to learn pairwise models only on 5day aggregation of data. We have updated the manuscript (both the text and the figures) to present these results.

(3) New results that subsample the drug groups to the same size as the control group. The conclusions about TIMP-1 treated mice hordes hold when we compare groups of the same size.

Recommendations for the authors:

Reviewer #1 (Recommendations For The Authors):

(1) COMPARISON WITH PREVIOUS WORK. The comparison with the cited previous work of Shemesh et al. 2013 rests novelty to the use of ME models in characterizing social interactions between groups of mice as well as sheds doubts on the main claim of the manuscript, namely that second-order correlations are sufficient to describe the joint distribution of occupancies of all mice (in particular triplets; there is no quantification of the variance explained by model in panel Fig. 2D). In my view, to make the claim "These results show that pairwise interaction among mice are sufficient to assess the observed collective behavior", the authors should compare models with 2nd and 3rd order interactions and quantify how much of the total correlation can be explained by pair-wise interactions, triplet interactions, and so on. Without a proper model comparison, it is unclear how the authors can make such a claim. One thing observed by Shemesh et al. is that, on average, J_ij are negative. This does not seem to be the case in the current study and the authors should discuss why.

Finally, the explanation provided in the Discussion about this discrepancy (spatial resolution and different group size) are not completely satisfactory. With more animals, one would imagine that the impact of higher order correlations would increase (and not decrease) as the number of terms of 3rd, 4th, ... order will be very big. I would also think that the same could be true for the spatial scale: assessing interactions with a coarser spatial grid (whole cages in the case of the ECO-Hab) would allow for simultaneous interactions among more mice to happen compared with a situation in which the spatial grid is so small that only a few animals can fit in each subdivision.

We thank the reviewer for the recommendation. In the updated version of the manuscript, we explicitly learn the triplet interaction model. We show that because the number of mice in our experiment is much larger than Shemesh et al., a triplet model runs into the problem of overfitting.

In particular, we found that the test set likelihood increases monotonically when the L2 regularization strength increases, which corresponds to a suppression of the triplet interaction strength (see additional supplementary figure, now Figure 2 - figure supplement 5). More specifically, for the range of regularization strength (β_G) we tested (10^-1 < β_G < 10¹), the maximum test set likelihood is achieved at β_G = 10¹, which corresponds to 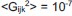. Notice that those learned triplet interactions are very close to zero. This means we should select a model with pairwise interactions over a model with triplet interactions.

We have added the above reasoning in page 5, line 166-169 of the Results section with the sentence “Moreover, models with triplet interactions show signs of overfitting under crossvalidation, which is mitigated when the triplet interactions are suppressed close to zero using L2 regularization”, a new subsection “Maximum entropy model with triplet interactions” in Materials and Methods (page 16-17, line 548 - 563) to describe the protocols of learning and crossvalidation for these triplet interaction models.

Furthermore, we extended the discussion about the difference between Shemesh et al. and our results in the Discussion section. In addition to the difference of spatial scales (chamber vs. location in the chamber), and the difference of group size and its impact on data analysis (N = 15 in our largest cohort and N = 4 in theirs), we added a discussion about the difference of experimental arena, which in Eco-HAB contains connected chambers that mimic the naturalistic environment, and in Shemesh et al. contains a single chamber. The change in the text is on page 12, between line 390 and line 394.

We thank the reviewers for pointing out that the mean 2nd order interaction in Shemesh et al. is negative. One possibility is that the labeled areas in Shemesh et al. are much smaller than in our Eco-HAB setup, which could suggest that mice do have the space to stay in the same area, which will lead to a negative mean 2nd order interaction.

(2) ASSESSMENT OF THE TEMPORAL EVOLUTION OF THE INTERACTIONS. The analysis of the stability of the social structure is not conclusive. First, I don't think the authors can conclude that "These results suggest that the structure of social interactions in a cohort as a whole is consistent across all days." If anything is preserved, they would be the statistics of that structure but not the structure itself (i.e., there is no evidence for that). The comparison of the stability of the mean <h_i> and the mean <J_ik> would also require a statistical test to be able to state that "Delta h_i changed more strongly from day to day (Fig. 3D, top panel) relative to the interaction measured as the Jij's." The same is true for the assessment of the TIMP: the differences found in the variability in J_ij and in the mean and variance of the h_i's, look noisy and would require a proper statistical test. The traces look quite variable across days in the control condition, so assessing differences may be difficult. Finally, it would be good to know if the variability in individual J_ij is because they truly vary from day to day or because estimating them within one day is difficult (statistical error). If the reason is the latter, one could decrease the temporal resolution to 2-3 days and see whether the estimated J_ijs are more stable. Perhaps, also for that reason, the summed interaction strength J_i is also more stable, simply because it aggregates more data and has a smaller statistical error.

We thank the reviewer for pointing out the necessity of assessing the temporal evolution of the interactions. The problem of shorter data duration leads to more noise in the estimation, together with the reviewer’s Comment 4 about the risk of overfitting, led us to add a new Results subsection “Choosing timescales for analysis” (page 6, line 171 to line 189). Specifically, we assess whether the pairwise maximum entropy model overfits using data from _K-_day aggregates, by computing the log-likelihood of both the training sets and the test sets,which is chosen to be 1 hour from the 6 hour data window of each day. We found that for single day data, the pairwise maximum entropy model overfits. In contrast, for data with aggregates of more or equal to 4 days of data, the pairwise model does not overfit. This new result is supported by an additional supplementary figure, now Figure 2 - figure supplement 6.

To be consistent with later approaches in the manuscript where we consider the effects of TIMP1, we choose the analysis windows to be data aggregates from 5 days. This means for the experiment that collects a total of 10 days of data, there are only two time points, thus a study of the temporal evolution is limited to comparison between the first 5 days and the last 5 days of the experiment. We describe these results in the Results subsection “Stability of sociability over time” (page 6, line 190 - 220). An additional supplementary figure, now Figure 2 - figure supplement 7, shows in details the comparison of the inferred interaction strength J and the chamber preference between the first 5 days and the last 5 days for the 4 cohorts of male C57BL6/J mice, which shows the inferred interactions have a consistent variability across first and last 5 days, and across all cohorts. The small value of Pearsons’ correlation coefficient shows that the exact structure (pairspecific J_ij) is not stable. At the end of the Results subsection “Stability of sociability over time”, we explicitly say that “This implies that the maximum entropy model does not infer a social structure that is stable over time.”

(3) EFFECT OF TIMP-1. The reported effects of TIMP-1 on the variance of the J_ij seem very small and possibly caused by a few outlier J_ijs (perhaps from one or two animals) which

are not present in the control group which seems to have fewer animals (N = 9 minus two mice that died after the surgery vs. N = 14 in the drug group), so the lack of a significant difference in the sigma[J_ij] could simply be due to a smaller N (a test for the interaction group x drug was not done).

The clearest effect of TIMP-1 seems to be a change in place preference (h_i) and not the interaction terms (J_ij) (Fig. 3F bottom). But this could be explained by a number of factors that have nothing to do with sociability such as that recovery from surgery makes them eat more/less. The fact that it seems to be present, as recognized by the authors, in the control group with no TIMP-1 and that this effect was not observed in the female group F1, puts into question the specificity and reproducibility of the result.

Finally, the effect of TIMP-1 in the DTI would require more statistics (testing the interaction group x drug). The fact that the control group has fewer animals (N = 9 vs. 15 and 13 in the drug groups), and that there is a weaker trend in the DTI of the control group to start high and then decrease, makes this test necessary.

Now, after we select a proper timescale to learn the pairwise maximum entropy model, we update the manuscript to present results only on 5-day aggregation of data (see updated Figure 3, updated supplementary figures, Figure 3 - figure supplement 1 and 2). For the variance of the J_ij, the F-test between different 5-day aggregates before and after TIMP for the male drug group now shows a nonsignificant p-value after applying the Bonferroni correction. For the female drug group, the difference of the J_ij variance is still significant.

To test the effect of different group size on DTI, we subsampled the drug groups by 1) subsampling the inferred interactions learned from the original N = 15 or N = 13 data, or 2) subsampling the mice colocalization data and then inferring the pairwise interactions. In both cases, the resulting DTI for the subsampled drug group still exhibits the same global pattern as before, i.e. after TIMP-1 injection, DTI significantly increases, which after 5 days falls back to the baseline level. The results are supported by two additional supplementary figures, Figure 4 - figure supplement 1 and 2. This result is referred to in the text in the Results subsection “Impaired neuronal plasticity in the PL affects the structure of social interactions” (page 10, line 333 - 336): “Notably, the difference of the DTI is not due to the control group M4 has less mice, as subsampling both on the level of the inferred interactions (Figure 4 - figure supplement 1) and on the level of the mice locations (Figure 4 - figure supplement 2) give the same DTI for cohorts M1 and F1.”

(4) MODEL COMPARISON. Any quantitative measure of "goodness" of the model , (i.e., comparison of the predictions of the model with triplet frequency as well as the distribution of p(K)) should be cross-validated. In particular, Fig. S2 needs to be cross-validated for the goodness of fit to be properly quantified. Is the analysis shown in Fig. 3F crossvalidated? Because otherwise, there is an expected increase in the likelihood simply explained by an increase in the number of parameters of the model (i.e., adding the J_ij's).

As discussed in our responses to Comment 1 and 2, we have added results about cross-validation in the new supplementary figures, Figure 2 – figure supplement 5 and 6 , for which we computed the test-set and training-set likelihood for maximum entropy models with pairwise interactions and also for models with triplet interactions. Figure 2 - figure supplement 6 shows the pairwise model does not overfit when we consider the aggregated data from more or equal to 4 days.

(5) EFFECT OF SLEEP. The comparison of p(K) between the data and the model requires a bit more investigation: the model underestimates instances in which almost all mice were in the same compartment (i.e., for K >= 13. p(K)_data >> p(K)_MEM; btw where is the pairwise point p(15) in Fig. 2E and Fig. S4?). Could this be because there were still short periods during the dark cycle in which all mice were asleep in one of the cages? As explained by the authors, sleep introduces very strong higher order correlations between animals as they like sleeping altogether. Knowing whether removing light periods was enough to remove this "sleep contamination" or not, would be important in order to interpret discrepancies between the pairwise model and the data.

Figure 2E shows that the pairwise maximum entropy model (in black) overestimates the data (in blue circles) for P(K) at large K (and not underestimates). In the data, we never observe all 15 mice being in the same box; hence P_data(15) = 0, and does not show up in the log-scaled figure (same for Figure 2 - figure supplement 3). A possible explanation for the pairwise model overestimating P(K) at large K is that the finite-sized box limits the total number of mice that are comfortably staying in the same box. It can also be due to the fact that the number of time points at which K >= 13 is small and hence causes an underestimation due to finite data. We have added this interpretation of the discrepancy of P(K) to Section “Pairwise interaction model explains the statistics of social behavior” in page 6, line 160.

We thank the Reviewer for raising the point of “sleep contamination”. Indeed, Eco-HAB data, as do data from other 24h-testing behavioral systems, demonstrate distinct differences in activity levels during the light and dark phases of the light-dark cycle (Rydzanicz et al., EMBO Mol. Med., 2024). During the light phases, mice primarily sleep and, as noted, they huddle, so many individuals within the cohort tend to remain in close proximity for extended periods. We acknowledge that including such periods in the analysis could potentially introduce confounding effects to the model due to limited movement and interactions, and this is why we decided not to use this data. However, during the dark phases, mice are highly active, with individuals rarely staying in the same compartment for long periods. Specifically, in the dark phases, while there are occasional instances where a few mice may remain in the same compartment for over 1 hour, the majority exhibit considerable mobility, actively exploring and transitioning between compartments. We see no compelling reason to exclude these periods from our analysis, as such activity aligns with the natural behavioral repertoire of the mice and provides robust data for our model. Furthermore, it is well-established that mammals, including nocturnal species such as mice, are most active shortly after waking, typically at the onset of their active phase (i.e., the beginning of the dark phase). To ensure a conservative approach, we specifically analyzed the first 6 hours of the dark phase when the cumulative number of box visits is at its peak, indicating heightened activity levels. In our view, this period offers an optimal window for studying natural behaviors, including social interactions.

Additionally, prior studies using the Eco-HAB system have consistently demonstrated that mice engage in social interactions both within the compartments and in the connecting tubes during the dark phase (Puścian et al., eLife, 2016, Winiarski et al. in press). Given this evidence and the observed behavioral dynamics in our data, the likelihood of mice being asleep during the analyzed periods of the dark phase is very low.

We hope this clarification addresses the reviewer’s concerns and highlights the rationale underpinning our analysis choices. Thank you for raising this important point, which allowed us to provide additional context for our approach.

(6) COMPARTMENT PREFERENCES. The differences between p(K) across compartments also would require a bit more attention: of a MEM with non-spatially dependent pair-wise interactions shows differences across compartments, it must be because of the terms h_{i,r} terms which contain a compartment index, right? Wouldn't this imply that the independence model, which always underrepresents data events with large K, already contains the difference in goodness of fit between compartments (1, 3) and (2, 4)? In the plots, it does not look like the goodness of the independent model depends on the compartment (the authors could compare directly the models' predictions between compartments). Moreover, when looking at Fig. 2C, it does not look like the value of h_{i,r} in compartments (1,3) is higher than in (2,4) (if anything, it would be the other way around). How can this be explained? It would be good to know if the difference across compartments comes from differences in the empirical p(K) or in the models' prediction? If the difference is in the data p(K), could it be that the compartments 2-4 showing higher p(K=15) (i.e., larger difference with the pairwise MEM prediction) are those chosen by mice to sleep during the light cycle? If not, what could explain these differences across compartments? Could the presence of food and water explain this difference?

The reviewer is correct, in the pairwise MEM, the difference across compartments enter in the box preference h_ir. Greater h_ir means compartment r is more attractive to mouse i. Because box 2 and 4 contain food and water, we expect that mice are more attracted to box 2 and 4, and this is what we see in Figure 2C, bottom subpanels. To reduce the number of parameters to look at, we introduce an index Δh_i = h_i2 + h_i4 - h_i1 - h_i3. This index Δh_i is found to be mostly positive (see updated Figure 3C), which makes sense because mice are attracted to food and water.

Next we analyze the difference of P(K) across compartments (Figure 2 - figure supplement 3). There is already a difference in the P(K) calculated from empirical data. For example, P(K) in compartment 2 has a maximum at K = 5 while P(K) in compartment 1 has a maximum at K = 3.

One interesting observation is that it seems from Figure 2 - figure supplement 3 that the pairwise model explains P(K) in compartment 1 and compartment 3 better than in compartment 2 and in compartment 4. In compartment 2 and 4, the pairwise MEM overestimates P(K) for large K. An alternative MEM could include compartment-specific interaction strength, but it will also introduce 315 new parameters for a mice cohort with size N = 15.

MINOR

(1) A more quantitative comparison between in-cohort sociability and couplings J_ij as œwell as mean rates and parameters h_i is required. The matrices in Fig. 2C do look similar. So it is not clear how the comparison between these values is contributing to characterizing the correlation structure of the data.

The comparison between in-cohort sociability and coupling J_ij is given by supplementary Figure 2 - figure supplement 2. The key point for the model with the learned J_ij reproducing the in-cohort sociability is given by Figure 2 - figure supplement 1.

(2) Analysis of "in-state" probability is not explained. To me, it wasn't obvious what Fig. S5 is showing. I was assuming that this analysis was comparing the prediction of the MEM about the position of each animal at each time point, given its preference (h), pairwise interactions (J_ij), and the position of all other animals and the true position of the animal. But it seems like it is comparing the shape of the distribution of this prob across time between the data and the model (I guess the data had to be temporally binned in coarser temporal periods to yield prob values other than 0s and 1s). Also, not clear whether this analysis was done for each compartment separately and then averaged. This needs explanation.

The in-state probability is comparing the prediction of the MEM about the position of each animal at each time point, given its preference (h), pairwise interactions (J_ij), and the position of all other animals and the true position of the animal. To achieve values between 0s and 1s, we bin the data temporally according to the model-predicted in-state probability.

We have added the explanation of in-state probability on page 6, line 163-166. We have also improved the description of in-state probability in Materials and Methods (subsection “Comparing in-state probability between model prediction and data”, line 493 - 503, page 15), and added a pointer from the main text to it.

(3) Looks like Fig. S3 is not cited in the text.

We added a pointer to Fig. S3 (now Figure 2 - figure supplement 2) in line 154.

(4) The authors say that "TIMP-1 release from the TIMP-1-loaded nanoparticles diminishes after 5 days." Does that mean from the day of the injection (4-5 days before the "After Day 1") or five days after reintroduced in the ECO-Hab?

It means five days after the mice were re-introduced in the ECO-Hab. We have updated the text in Results/Effects of impairing neuronal plasticity in the PL on subterritory preferences and sociability (the end of the first paragraph of this subsection) to

“The choice of five-day aggregated data for analysis is in line both with the proper timescales needed for the pairwise maximum entropy model to not overfit, and with the literature that TIMP-1 release from the TIMP-1-loaded nanoparticles is stable for 7-10 days after injection (Chaturvedi et al., 2014) (i.e. 2-5 days after the mice are reintroduced to Eco-HAB).” (line 272 - 276, page 9)

(5) In Methods, the authors should report the final N of each of the three groups.

The number of final N is reported in Table 1 (page 13). In the updated version, we have added a pointer to Table 1 in Materials and Methods/Animals, and in Materials and Methods/Exclude inactive and dead mice from analysis. We have also expanded the caption of Table 1 to clarify the difference between final N and initial N, and added a pointer to Materials and Methods/Exclude inactive and dead mice from analysis.