Author response:
The following is the authors’ response to the original reviews.
Public Reviews:
Reviewer #1 (Public Review):
The paper proposes an interesting perspective on the spatio-temporal relationship between FC in fMRI and electrophysiology. The study found that while similar network configurations are found in both modalities, there is a tendency for the networks to spatially converge more commonly at synchronous than asynchronous time points. However, my confidence in the findings and their interpretation is undermined by an apparent lack of justification for the expected outcomes for each of the proposed scenarios, and in the analysis pipeline itself.
Main Concerns
(1) Figure 1 makes sense to me conceptually, including the schematics of the trajectories, i.e.
Scenario 1: Temporally convergent, same trajectories through connectome state space
Scenario 2: Temporally divergent, different trajectories through connectome state space
However, based on my understanding I am concerned that these scenarios do not necessarily translate into the schematic CRP plots shown in Figure 2C, or the statements in the main text:
For Scenario 1: "epochs of cross-modal spatial similarity should occur more frequently at on-diagonal (synchronous) than off-diagonal (asynchronous) entries, resulting in an on-/off-diagonal ratio larger than unity"
For Scenario 2: "epochs of spatial similarity could occur equally likely at on-diagonal and off-diagonal entries (ratio≈1)"
Where do the authors get these statements and the schematics in Figure 2C from? Are they based on previous literature, theory, or simulations?
I am not convinced based on the evidence currently in the paper, that the ratio of off- to on-diagonal entries (and under what assumptions) is a definitive way to discriminate between scenarios 1 and 2.
For example, what about the case where the same network configuration reoccurs in both modalities at multiple time points? It seems to me that one would get a CRP with entries occurring equally on the on-diagonal as on the off-diagonal, regardless of whether the dynamics are matched between the two modalities or not (i.e. regardless of scenario 1 or 2 being true).
This thought experiment example might have a flaw in it, and the authors might ultimately be correct, but nonetheless, a systematic justification needs to be provided for using the ratio of off- to on-diagonal entries to discriminate between scenarios 1 and 2 (and under what assumptions it is valid).
In the absence of theory, a couple of ways I can think of to gain insight into this key aspect are:
(1) Use surrogate data for scenarios 1 and 2:
a. For scenario 1: Run the CRP using a single modality. E.g. feed in the EEG into the analysis as both modality 1 AND modality 2. This should provide at least one example of CRP under scenario 1 (although it does not ensure that all CRPs under this scenario will look like this, it is at least a useful sanity check)
b. For scenario 2: Run the CRP using a single modality plus a shuffled version. E.g. feed in the EEG into the analysis as both modality 1 AND a temporally shuffled version of the EEG as modality 2. The temporal shuffling of the EEG could be done by simply splitting the data into blocks of say ~10s and then shuffling them into a new order. This should provide a version of the CRP under scenario 2 (although it does not ensure that all CRPs under this scenario will look like this, it is at least a useful sanity check).
(2) Do simulations, with clearly specified assumptions, for scenarios 1 and 2. One way of doing this is to use a simplified (state-space) setup and randomly simulate N spatially fixed networks that are independently switching on and off over time (i.e. "activation" is 0 or 1). Note that this would result in a N-dimensional connectome state space.
The authors would only need to worry about simulating the network activation time courses, i.e. they would not need to bother with specifying the spatial configuration of each network, instead, they would make the implied assumption that each of these networks has the same spatial configuration in modality 1 and modality 2.
With that assumption, the CRP calculation should simply correspond to calculating, at each time i in modality 1 and time j in modality 2, the number of networks that are activating in both modality 1 and modality 2, by using their activation time courses. Using this, one can simulate and compute the CRPs for the two scenarios:
a. Scenario 1: where the simulated activation timecourses are set to be the same between both modalities
b. Scenario 2: where the simulated activation timecourses are simulated separately for each of the modalities
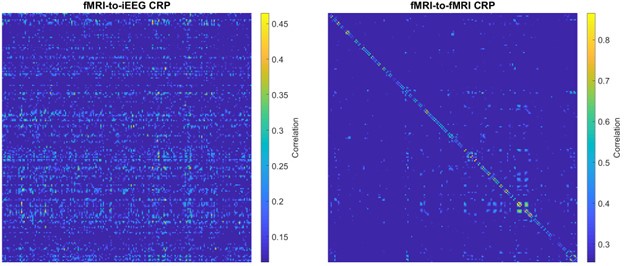
We thank the reviewer for raising this important matter as it directly relates to our study hypothesis. To address this point, we chose to focus on the first of the two alternative suggestions of the reviewer, as it provides evidence based on empirical data. In line with the reviewer’s suggestion 1, recurrence plots have indeed been previously applied to connectome dynamics data from the same modality [Hansen et al., NeuroImage 2015; Fig. 2B]. As shown in the referenced study, where the recurrence plot has been estimated within fMRI connectome dynamics, the on-diagonal entries have noticeably larger correlation values in comparison to off-diagonal entries. As the authors state, this contrast emphasizes the autocorrelation of connectome dynamics in their single modality recurrence plot. Extending these findings to our cross-modal recurrence plots, more synchronicity of connectome dynamics across fMRI and EEG will -by theory- translate into stronger correlation values along the diagonal axis as it represents neighboring timepoints in the data. On the other hand, less cross-modal synchronicity translates to a lack of such correlation prevalence along the diagonal axis.
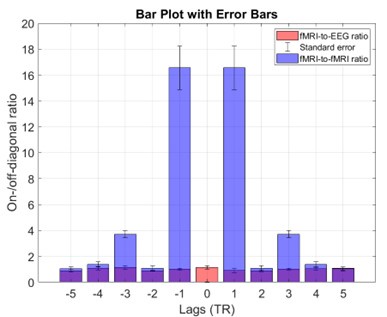
Complementing these statements with empirical data, Author response image 1 shows the fMRI-to-iEEG and fMRI-to-fMRI CRPs side by side as suggested by the reviewer. For simplicity, we thresholded each CRP at the top 5% of entries and calculated their corresponding on-/off-diagonal ratios. The on/off-diagonal ratio for fMRI-to-fMRI CRP was 4.32 ± 6.26 across -5 to +5 TR lags (with a maximum of 16.56 at a lag of one TR), while this value was 1.00 ± 0.31 for fMRI-to-iEEG CRP. Thus, it becomes apparent that synchronicity of connectome dynamics directly translates to the on-/off-diagonal ratio in CRP.
Author response image 1.
Sample CRP shown for a subject for comparing two cases: fMRI-to-iEEG (left) and fMRI-to-fMRI (right). The comparison shows that in the presence of genuine synchronous connectome dynamics, as expected for the within-molality case (right panel), the on-/off-diagonal ratio is expected to show noticeably higher values. This figure establishes a strong link between our proposed metric of on-/off-diagonal ratio and the extent of synchronicity of connectome dynamics.
Author response image 2.
On-/off-diagonal ratio in the fMRI-to-fMRI recurrence plot is considerably higher than the cross-modal fMRI-to-iEEG case. Horizontal axis shows the lag where the metric was calculated in the CRP. The bars reflect the group average metric while the whickers show standard deviation. Note that for the within-modality case, ratio is not defined at lag zero because of identical connectome frames.
(2) Choices in the analysis pipeline leading up to the computation of FC in fMRI or EEG will affect the quality of information available in the FC. For example, but not only, the choice of parcellation (in the study, the number of parcels is very high given the number of EEG sensors). I think it is important that we see the impact of the chosen pipeline on the time-averaged connectomes, an output that the field has some idea about what is sensible. This would give confidence that the information being used in the main analyses in the paper is based on a sensible footing and relates to what the field is used to thinking about in terms of FC. This should be trivial to compute, as it is just a case of averaging the time-varying FCs being used for the CRP over all time points. Admittedly, this approach is less useful for the intracranial EEG.
We agree with the reviewer on ensuring that the time-averaged FC aligns with expectations of the field and prior work. For this reason, our supplementary analysis already included an analysis that replicates the well-established (albeit modest) spatial similarity between fMRI static connectome and EEG/iEEG static connectomes:
“In scalp EEG-fMRI data, cross-modal spatial (2D) Pearson correlation of group-level time-averaged connectomes between fMRI and EEG-FCAmp or fMRI and EEG-FCPhase were calculated across all frequency bands. The average spatial correlation value across frequency bands r = 0.28 and r = 0.28 for EEG-FCAmp and EEG-FCPhase, respectively. The spatial correlation values across all frequency bands and connectivity measures were significantly higher than the corresponding null distributions generated by phase-permuted group-level fMRI-FC spatial organization (p<0.005; 200 repetitions; FDR-corrected at q<0.05 for the number of frequency bands). …. Of note, the small effect sizes are strongly in line with prior literature (Hipp and Siegel, 2015; Wirsich et al., 2017; Betzel et al., 2019) and may point to possible divergence in the dynamic domain as investigated in the main manuscript.”
This replication directly confirms the validity of our selected atlas for further investigations into the connectome dynamics. We acknowledge that with 64 EEG channels, one can only estimate a relatively coarse connectome. Among the well-known coarse atlases, we chose the Desikan-Killiany atlas as it is based on anatomical features, eliminating possible biases towards a particular functional data modality. Moreover, this atlas has been commonly used for multimodal functional connectivity studies, facilitating the confirmation of prior findings in the time-averaged domain [Deligianni et al. Front. Neurosci 2104, Wirsich et al. NeuroImage, 2020, Wirsich et al., NeuroImage 2021].
(3) Leakage correction. The paper states: "To mitigate this issue, we provide results from source-localized data both with and without leakage correction (supplementary and main text, respectively)." Given that FC in EEG is dominated by spatial leakage (see Hipp paper), then I cannot see how it can be justified to look at non-spatial leakage correction results at all, let alone put them up front as the main results. All main results/figures for the scalp EEG should be done using spatial leakage-corrected EEG data.
We agree that relying on leakage-uncorrected scalp EEG alone would be problematic. It is for this reason that the intracranial data constructs the core of our results, emphasizing that the observed multiplex architecture of connectomes is indeed present in the absence of source leakage. Only when this finding is established in the intracranial EEG, do we provide the scalp EEG data as a generalization to whole-cortex coverage connectomes of healthy subjects. Moreover, it is known that existing source-leakage correction algorithms may inadvertently remove some of the genuine zero-lag connectivity. For instance, Finger and colleagues have shown that the similarity of functional connectivity to structural connectivity diminishes after correction for source-leakage (Finger et. al, PLOS Comp. Biol. 2016). Therefore, we have deliberately chosen to include our generalization findings before source-leakage correction (main text) as well as after source-leakage correction reflecting a more stringent approach (supplementary analysis). Importantly, our conclusions hold true for both before and after source-leakage correction.
Reviewer #2 (Public Review):
Summary:
The study investigates the brain's functional connectivity (FC) dynamics across different timescales using simultaneous recordings of intracranial EEG/source-localized EEG and fMRI. The primary research goal was to determine which of three convergence/divergence scenarios is the most likely to occur.
The results indicate that despite similar FC patterns found in different data modalities, the time points were not aligned, indicating spatial convergence but temporal divergence.
The researchers also found that FC patterns in different frequencies do not overlap significantly, emphasizing the multi-frequency nature of brain connectivity. Such asynchronous activity across frequency bands supports the idea of multiple connectivity states that operate independently and are organized into a multiplex system.
Strengths:
The data supporting the authors' claims are convincing and come from simultaneous recordings of fMRI and iEEG/EEG, which has been recently developed and adapted.
The analysis methods are solid and involve a novel approach to analyzing the co-occurrence of FC patterns across modalities (cross-modal recurrence plot, CRP) and robust statistics, including replication of the main results using multiple operationalizations of the functional connectome (e.g., amplitude, orthogonalized, and phase-based coupling).
In addition, the authors provided a detailed interpretation of the results, placing them in the context of recent advances and understanding of the relationships between functional connectivity and cognitive states.
Weaknesses:
Despite the impressive work, the paper still lacks some analyses to make it complete.
Firstly, the effect of the window size is unclear, especially in the case of different frequencies where the number of cycles that fall in a window will vary drastically. A typical oscillation lasts just a few cycles (see Myrov et al., 2024), and brain states are usually short-lived because of meta-stability (see Roberts et al., 2019).
We now replicate our results with an additional window size. Please see section “Recommendations for the authors”.
Secondly, the authors didn't examine frequencies lower than 1Hz despite similarities between fMRI and infra-slow oscillations found in prior literature (see Palva et al., 2014; Zhang et al., 2023).
We address this issue below. Please see section “Recommendations for the authors”.
On a minor note, the phase-locking value (PLV) is positively biased for EEG data (see Palva et al., 2018) and a different metric for phase coupling could be a more appropriate choice (e.g., iPLV/wPLI, see Vinck et al., 2011).
While iPLV and wPLI are not positively biased, they may reduce genuine zero-phase connectivity as they were initially designed to address spurious zero-phase connectivity from source leakage in scalp EEG. Indeed, PLV connectivity is shown to be more strongly correlated with structural connectivity than wPLI and other phase coupling methods [Finger et al., PLOS Comp. Biol. 2016], emphasizing that it contains genuine connectivity that may be lacking when zero-phase connectivity is removed. We chose PLV because it is a widely used functional connectivity metric, particularly in intracranial data where source leakage is not a critical concern. Thus, using PLV facilitates cross-study comparisons including to our prior work [e.g. Mostame et al. NeuroImage 2020, Mostame et al. J Neurosci 2021].
The repository with the code is also unavailable.
Thank you for bringing this to our attention. We have now made our repository publicly accessible at: https://github.com/connectlab/Mostame2024_Multiplex_iEEG_fMRI.
Recommendations for the authors:
Reviewer #1 (Recommendations For The Authors):
The window widths used to compute FC as a function of time are an important aspect, so I feel that this should be briefly described up-front in the main Results text.
Methods. "Finally, to compensate for the time lag between hemodynamic and neural responses of the brain (Logothetis et al., 2001), we shifted the fMRI-FC time course 6 seconds backwards in time." What about the effects of temporal blurring from the HRF? Do we need to care about that?
We agree with the importance to investigate the effect if temporal blurring of the HRF. The main text already included a replication of findings from CRPs generated using fMRI data and EEG amplitude signals convolved with the canonical HRF. This method serves as an alternative to the 6-second shifting. Both approaches produced similar results.
Methods. In fMRI connectome computation it is common to look at partial correlation rather than full correlation. Partial correlation focuses more on direct connections. It would be good if the paper acknowledged and justified why it is OK to use full correlation.
We have now added a brief explanation in this regard in the main text (Methods section) as follows:
“In fMRI connectome computation, some prior work has used partial correlation instead of full correlation. Partial correlation emphasizes direct connections by calculating correlation between any pair of bran regions after regressing out the timeseries of all other regions. However, we have opted to use full correlation because this permits interpretation of our outcomes in the context of the vast existing literature that uses full correlations in fMRI including the majority of bimodal (EEG-fMRI) connectome studies (e.g. Tagliazucchi et al., 2012; Deligianni et al., 2014; Wirsich et al., 2017b, 2020, 2021; Allen et al., 2018).”
The paper should relate the results to findings showing clear links between simultaneously recorded EEG and fMRI beyond FC. E.g. Mantini (PNAS) 2007 and Van De Ville (PNAS) 2010 to name two.
In line with this important point, we have extended the existing discussion section that compares our outcomes to EEG-fMRI beyond functional connectivity:
“Prior multi-modal studies of neural dynamics have predominantly aimed at methodologically cross-validating hemodynamic and electrophysiological observations, thus focusing on their convergence. These important foundational studies include e.g., the cross-modal comparison of region-wise (Mukamel et al., 2005; Nir et al., 2007) or ICN-wise (Mantini et al., 2007) activity fluctuations, instantaneous activity maps (Hunyadi et al., 2019; Zhang et al., 2020) or EEG microstates (Van de Ville 2010), infraslow connectome states (Abreu et al., 2020), or connection-wise FC including studies in the iEEG-fMRI and scalp EEG-fMRI data used in the current study (Ridley et al., 2017; and Wirsich et al., 2020, respectively). In contrast to this prior work, the current study investigated the highly time-resolved cross-modal temporal relationship at the level of FC patterns distributed over all available pairwise connections, and found a connectome-level temporal divergence. The discrepancy between temporal divergence in our study and convergence in prior studies implies that infraslow fluctuations of activity in individual regions or of FC in individual region-pairs observable in both modalities (prior studies) are neurally distinct from connectome-wide FC dynamics observable separately in each modality (current study). Indeed, we confirmed the existence of infraslow electrophysiological FC dynamics driving cross-modal temporal associations at the level of individual connections (Fig. S3) …”
Reviewer #2 (Recommendations For The Authors):
(1) Check different window sizes and stability of the FC patterns as a function of it.
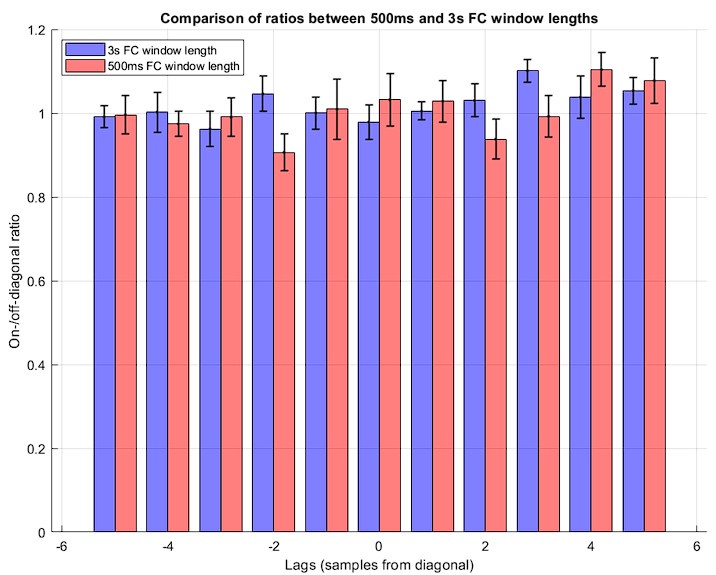
We thank the reviewer for the helpful feedback. We agree that the window size could possibly affect the estimation of individual connectome frames, particularly given that neural processes unfold at hundreds of milliseconds rather than seconds. However, we expect that the asynchronous nature of cross-modal convergence observed in our data would remain intact regardless of the specific window length used for FC calculations. To confirm this, we replicated some of our main analyses in the iEEG-fMRI data with a window length of 500ms (as opposed to 3s, equivalent to one TR) as follows:
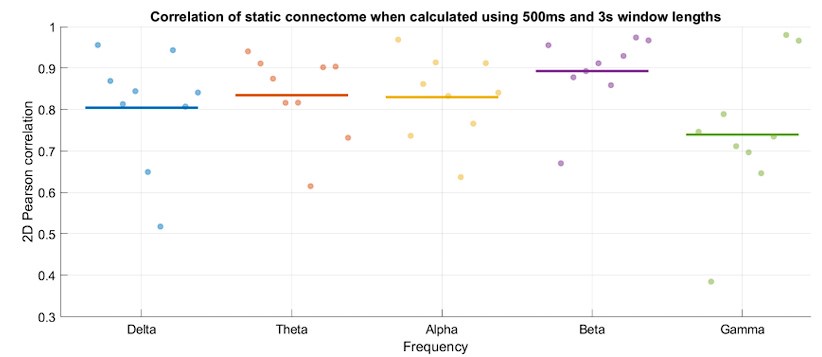
First, we showed that changing the window length does not substantially impact the overall architecture of the connectomes (Author response image 3). Particularly, the time-averaged connectome patterns across different frequency bands were all strongly correlated between the two analyses (500ms and 3s window lengths).
Author response image 3.
Time-averaged connectome patterns are highly replicable when calculated using 3s or 500ms window lengths. Horizontal axis represents frequency bands, while each dot represents a subject. Vertical axis shows 2D Pearson correlation of the two connectomes. The group average within each frequency band is marked by a horizontal line.
Second, we replicated our major findings of CRP and its on-/off-diagonal ratio in the iEEG-fMRI dataset using a window length of 500ms for FC calculations. Indeed, the data does not show a substantial difference in the on-/off-diagonal ratios of the CRP entries between the 3s and 500ms window lengths. Specifically, the ratio was equal to 1.02 ± 0.07 for 500ms window length, emphasizing absence of significant temporal convergence of the connectome dynamics (see Author response image 4). A paired t-test between group-averaged ratios across different lags confirms a lack of significant difference between the two analyses (p= 0.50). This finding further emphasizes the genuine asynchronous nature of connectome dynamics across the neural timescales measured in fMRI and electrophysiology. We have added this analysis to the supplementary data.
Author response image 4.
On-/off-diagonal ratio is shown across lags for both analyses: 3s window length (blue) and 500ms window length (red). Each bar shows the mean across subjects, while the whiskers show the corresponding standard deviations.
(2) Try to decrease the lowest frequency of the analysis below 1Hz or just compute it for multiple log-spaced frequencies from infra-slow delta to high-gamma band.
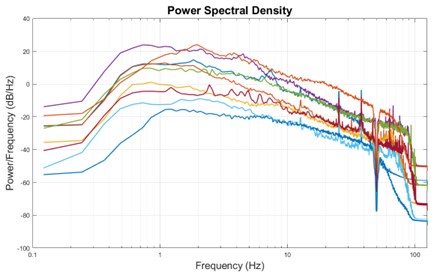
Thank you for pointing out this matter. We do not expect considerable signal in the frequency range below the current lower bound of delta (1Hz) because as in most other EEG recordings, EEG was not recorded in DC setting and has a hardware high-pass filter of 0.1Hz. Nonetheless, we investigated the power spectral density of our iEEG-fMRI data and found that there is indeed little signal power left in the available infraslow range [0.5 – 1 Hz] after the preprocessing steps (Author response image 5).
Author response image 5.
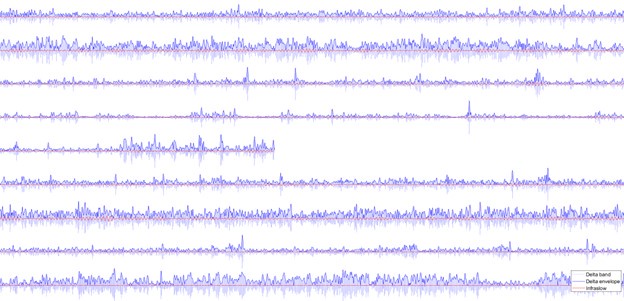
Power spectral density of all subjects in the fMRI-iEEG dataset shows lack of sufficient power in the infraslow range. Infraslow range signals are almost always filtered out during recording unless the recording setup includes a DC amplifier. The infraslow signal of EEG that is often considered correlated with the fMRI signals in the literature most commonly are extracted from the slow-changing envelope of the bandlimited signals, like envelope of gamma oscillations.
Accordingly, when the iEEG signals are filtered within the range of [0.5, 1], there is little signal variation observed in the signal timeseries, contrasting the adjacent delta band signal (Author response image 6). Importantly, the power envelope of the delta band (and all other canonical bands not shown here) comprise major fluctuations in the infraslow range, as expected. We would like to emphasize that the existing studies addressing infraslow EEG signal dynamics typically consider the infraslow envelope fluctuations of band-limited signals in traditional frequency bands [e.g. Nir et. al, Nat Neurosci 2008] rather than direct recordings in the infraslow frequency range. Investigating HRF-convolved EEG signals similarly captures the infraslow characteristics of the timeseries [e.g. Mantini et al. PNAS 2007, Sadaghiani et al., J Neurosci 2010] (and note that HRF-convolved analyses are included as supplementary investigation in the current study). To the best of our knowledge, very few studies have investigated direct infraslow EEG signals using DC EEG, and we are aware of only two DC-EEG studies with concurrent fMRI [Hiltunen et al., J Neurosci 2014, Grooms et al., Brain Connectivity 2017]. The infraslow correlates of fMRI in electrophysiological signals reported in prior work therefore reflect the slow changes in faster activity or connectivity of traditional frequency bands, which is indeed already included in the current study.
Author response image 6.
Sample timeseries of the iEEG signal of the nine subjects (nine rows) for a 400 second interval. Blue signals show the bandlimited delta with its envelope shown as darker blue. The red signal represents the infraslow signal component left in the data, which is much lower in power.