Tapered whiskers are required for active tactile sensation
- Janelia Farm Research Campus, Howard Hughes Medical Institute, United States
- Max Planck Institute for Brain Research, Germany
- Ben Gurion University, Israel
Figures
Figure 1
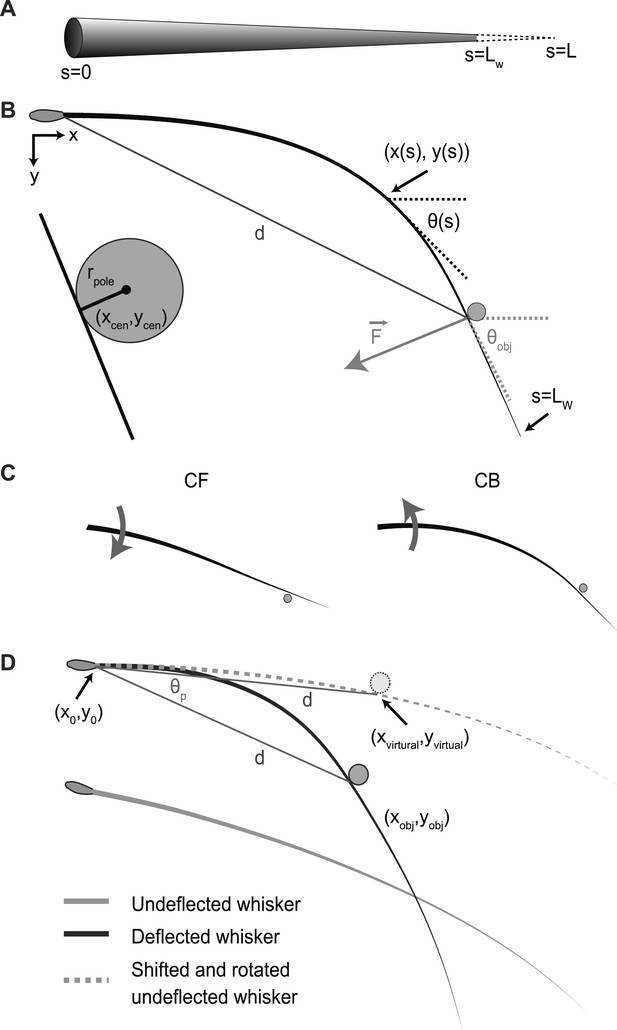
Schematic of the whisker in two dimensions.
(A) The whisker is modeled as a truncated cone of length LW, virtually extended to length L. (B) The base of the whisker (in the follicle, or attached to a galvo, Figures 4–6) is at point (x0, y0) and angle θ0, measured clockwise. The position of a point along the whisker is (x(s), y(s)) and its angle with the x-axis is θ(s). The contacted object is a cylindrical pole with radius rpole centered at (xcen, ycen); the pole and whisker are shown at a magnified scale in the inset on the left. The whisker contacts the object at the point (xobj, yobj) at an angle θobj. The object distance, d, is the distance between (xobj, yobj) and the whisker base. The pole applies a force on the whisker. (C) The concave forward (CF, left) and concave backward (CB, right) whisker configurations. Thick black lines, whiskers; solid circle, poles; gray arrows, movement directions. (D), Definition of the push angle, θp, which measures the strain on the whisker imposed by the object. The deflected and undeflected whiskers are shown as black and gray lines respectively. The pole is a dark gray circle. The undeflected whisker is translated and rotated in the plane such that it has the same x0, y0 and θ0 as the deflected whisker. This generates a virtual undeflected whisker (dashed gray line). A virtual pole (light gray circle) is generated by shifting the real pole such that it will be tangent to the virtual undeflected whisker. In addition, the distance from the contact point of the virtual unbent whisker and the virtual pole, (xvirtual, yvirtual) and the base (x0, y0) is equal to d, the distance between (xobj, yobj) and the base. The angle between the two line segments connecting the base with the real and virtual contact points is θp.
Figure 2
Interactions between whiskers and an object.
Solutions of the quasi-static model (Equations 8–14) for a conical whisker (A and B) and a cylindrical whisker (C and D). The pole is denoted by a gray circle. The resting shape of the whisker is y = Ax2, where A = 0.02 mm−1 (Quist and Hartmann, 2012), and the whisker touches the pole in the concave backward configuration. (A) Two solutions for a conical whisker. For θp = 10°, there are two solutions for whisker shape, one is stable (solid line) and one is unstable (dashed line). (B) Whisker shape at the saddle-node bifurcation (θp = 15.6°). There is only one solution as the stable and unstable solutions coalesce. The object touches the whisker not at the tip. For any larger θp, static solutions cease to exist and the whisker slips off the pole. (C) Whisker shape for a cylindrical ‘whisker’ and θp = 10°. Only one solution (stable) exists; the unstable solution is not physical because its computed arclength is longer than Lw = 20 mm. (D) For θp = 62.7°, the tip of the cylindrical ‘whisker’ reaches the object. Beyond this value of θp, the ‘whisker’ is pulled off the object. Parameters for all panels: Lw = 20 mm, rbase= 30 µm, rtip = 1.5 µm for the conical whisker and 30 µm for the cylindrical ‘whisker’, d=15.7 mm, E = 3 GPa, x0 = 0, y0 = 0. The pole has rpole=0.25 mm and its center is located at xcen = 15.13 mm, ycen = 4.29 mm.
Figure 3
Analysis of conical (A–E) and cylindrical whiskers (F–J) pushing into a pole.
(A) Schematic of a conical whisker. Parameters for panels (B–E): Lw = 20 mm, rbase= 30 µm, rtip = 1.5 µm, x0 = 0, y0 = 0, rpole = 0.25 mm, E = 3 GPa. The equation of the undeflected whisker is y = Ax2 where A = 0.02 mm−1 (Quist and Hartmann, 2012). For CB configurations, xcen = 15.13 mm, ycen = 4.29 mm; for CF configurations, xcen = 14.87 mm, ycen = 4.71 mm. Positive and negative values of θp correspond to CB and CF configurations respectively. (B) θobj as a function of θp. Left, concave forward (CF); right, concave backward (CB). Solid lines, stable solutions; dashed lines, unstable solutions (Equations 8–14). Solid circles denote saddle-node bifurcations (SNB). (C) Force F as a function of θp. (D) Location of object contact along the whisker arc, sobj, as a function of θp. Arrows correspond to Figure 2A (a) and Figure 2B (b, SNB). (E) The detachment curve in the θp−d plane bounds the parameter regime with a stable solution for a whisker contacting an object. Black lines represent the points when the stable solution coalesces with an unstable solution and disappears via a saddle-node bifurcation (slip-offs). Blue line represents the points where the whisker is pulled off because the tip has reached the object, sobj = LW (pull-offs). (F) Schematic of a cylindrical whisker. Parameters as for conical whisker, except that Lw = 20 mm, rbase= rtip = 30 µm. Panels (G–J) correspond to panels (B–E). Two object distances are considered in panels (G–I). Arrows in panel i correspond to Figure 2C,D. d = 15.7 mm (blue lines) corresponds to the pole location used in (B–D). The ends of the blue lines correspond to pull-offs. Additionally, an object distance d = 10 mm is shown (black lines). The black solid circles correspond to slip-offs (SNBs).
Figure 4
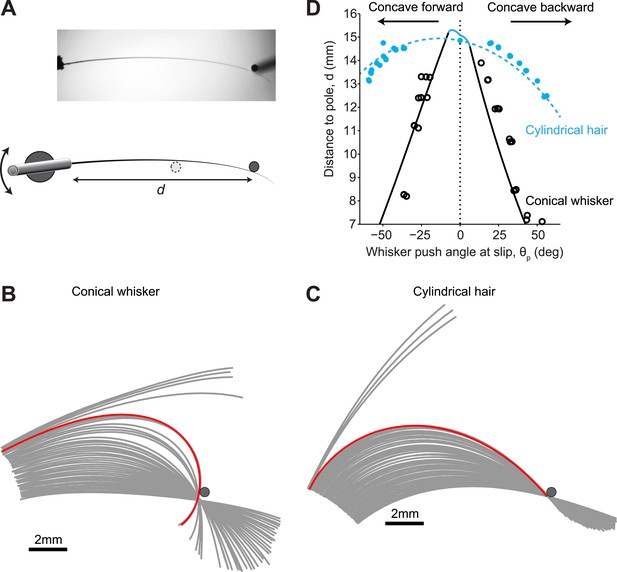
Isolated whiskers interacting with cylindrical poles.
(A) Top-down view of a mouse C2 whisker mounted on a galvanometer scanner. The scanner rotates the whisker into a vertical pole. The distance of the pole from the base of the whisker, d, is varied across experiments. (B) Snapshots of the whisker at 32 Hz as it is smoothly rotated (0.2 Hz, counter clockwise) into and past the pole. Red line, whisker shape immediately (<32 ms) before slip-off. Note that the end of the whisker had not reached the point of object contact. (C) Snapshots of a near-cylindrical hair. Red line, hair shape immediately before pull-off. Note that the end of the hair had reached the point of object contact. (D) The detachment curve in the θp−d plane. Solid line, theoretical prediction for conical whisker; open circles, experimental measurements for conical whisker. Dashed line, theoretical prediction for cylindrical hair; solid circles, experimental measurements for cylindrical hair. Blue, pull-offs occur because whisker tip has reached the object. Black, slip-offs occurs because of saddle-node bifurcation. Parameters of the conical whisker: Lw = 15.25 mm, rbase= 32.5 µm, rtip = 2 µm, A = 0.02 mm−1. Parameters of the approximately cylindrical hair: Lw = 15.0 mm, rbase= 30 µm, rtip = 26.5 µm, A = 0.017 mm−1. Pole radius, rpole = 0.25 mm.
Figure 5
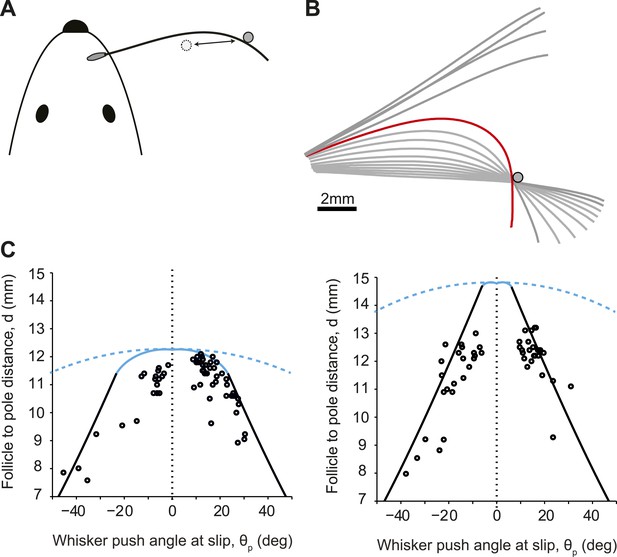
Slip-offs during object location discrimination behavior.
(A) Schematic of a mouse whisking to touch a pole (experiments from Pammer et al., 2013). (B) Time series (250 Hz) of whisker shape around example protraction slip event. Frame of slip-off is highlighted in red. (C) Detachment curves in the θp−d plane for two whiskers. Solid line, theoretical predictions for conical whisker; open circles, experimental measurements for conical whiskers. Dashed line, theoretical predictions for cylindrical hair. Blue, pull-offs. Black, slip-offs. Left, truncated whisker with parameters: Lw = 12.5 mm, rbase= 35 µm, rtip = 8.5 µm. Right, whisker parameters: Lw = 15.3 mm, rbase = 33.5 µm, rtip = 2 µm. For both whiskers, intrinsic curvature was y = A(x−2.2 mm)2 where A = 0.02 mm−1.
Figure 6
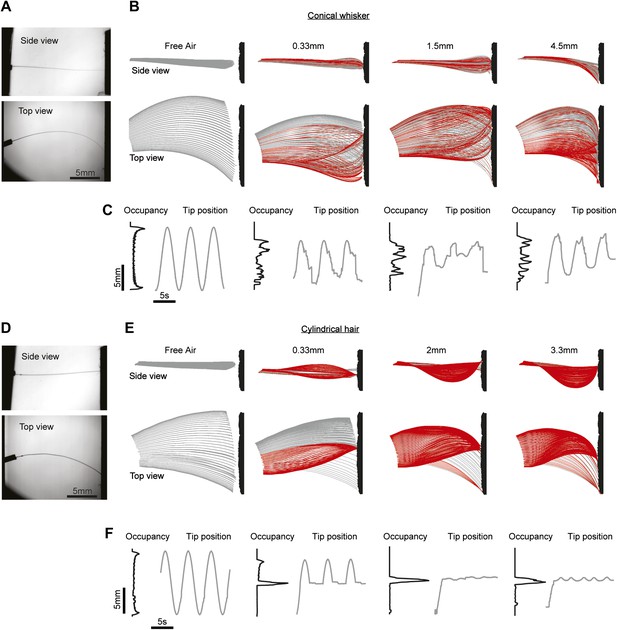
The whisker taper is necessary for slips across textures.
(A) Dual-perspective imaging of a conical whisker, mounted on a galvo, sweeping across a texture (600 grit sandpaper). ‘Top’, Side view; ‘Bottom’, Top view. (B) Conical whisker swept past the texture at four distances: Free air, push distance dp = 0.33 mm, 1.5 mm and 4.5 mm. dp = ||x(Lw)−x(0), y(Lw)−y(0)||−d, where d is the nearest distance from the base of the whisker to the surface. In other words, dp is the distance the surface is moved radially into the whisker beyond just touching. Red traces indicate frames where the whisker tip is stuck, gray traces where the tip is slipping along the surface. Surface texture is schematic and exaggerated. (C) Black lines, histograms of tip position over time. Gray lines, trajectories of the whisker tip over the first three whisking periods. Traces are aligned to peak of theta at base. (D–F), as (A–C), but using a cylindrical hair of similar length. Free air, push distance dp = 0.33 mm, 2 mm and 3.3 mm. Whisker parameters Lw = 16.4 mm, rbase= 33.5 µm, rtip = 2 µm. Hair parameters as in Figure 4.
Figure 7
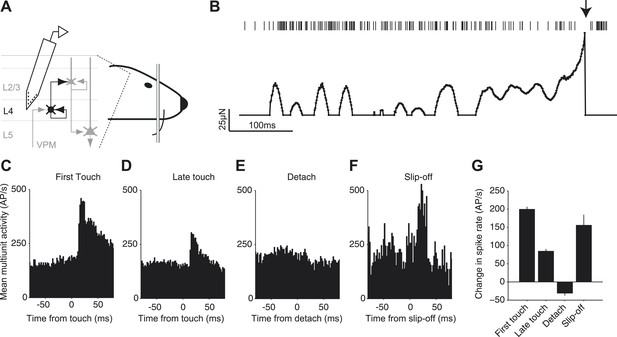
Neural signals of slip-off in the barrel cortex.
(A) Silicon probe recording during a pole localization task (experiments from O’Connor et al., 2013). (B) Spikes and whisker forces, one behavioral trial. ‘Top’, multi-unit activity. Arrow, slip-off event. ‘Bottom’, contact induced forces. Solid circles, time points with non-zero contact-mediated forces calculated from changes in whisker curvature. A 2 ms period during which the whisker was slipping off was removed as the quasi-static model is invalid for such highly dynamic events. (C–F) Multi-unit spike responses in the barrel cortex (shank < 300 μm from the center of the C2 barrel). (C) Activity aligned to the first touch in a trial (720 responses; two animals, three sessions, six electrode shanks). (D) Same as (C), but aligned to the last touch before a behavioral response (i.e., lick) (720 responses). (E) Same as (C), but aligned to the moment of detach on the last touch before a behavioral response in trials without slip-offs (392 responses). To prevent contamination by touch-onset this analysis was restricted to touches that were longer than 50 ms. (F) Aligned to slip-off (34 responses). (G) Change in spike rate triggered by the event (activity 10–30 ms post event, minus activity −50 to 0 ms pre event). Error bars, SEM. Pairwise comparison showed no significant difference in evoked spikes between first touch and slip-off groups (p=0.20), a significant difference between last touch and slip-off (p=0.037) and significant differences between all other groups (every pair, p<10−12).
Videos
Video 1
Example video of a conical whisker mounted on the galvo (Figure 4) slipping off a pole. Speed 16fps, 0.5x real-time.
Video 2
Example video of a cylindrical hair mounted on the galvo (Figure 4) pulling off a pole. Speed 16fps, 0.5x real-time.
Video 3
Composite video of the conical whisker mounted on a galvo slipping across the textured surface in Figure 6B (4.5 mm push distance). Upper video is the side view, lower video is the top view. Speed 32fps, 1x real-time.
Video 4
Composite video of the cylindrical hair mounted on a galvo getting stuck on the textured surface in Figure 6E (3.3 mm push distance). Upper video is the side view, lower video is the top view. Speed 32fps, 1x real-time.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Tapered whiskers are required for active tactile sensation
eLife 2:e01350.
https://doi.org/10.7554/eLife.01350
