The inherent mutational tolerance and antigenic evolvability of influenza hemagglutinin
- Fred Hutchinson Cancer Research Center, United States
Figures
Figure 1
Schematic of the deep mutational scanning experiment.
The Illumina deep-sequencing samples are shown in yellow boxes (DNA, mutDNA, virus, mutvirus). Experimental steps and associated sources of mutations are shown in blue text, while sources of error during Illumina sample preparation and sequencing are shown in red text. This entire process was performed in biological triplicate.
Figure 2
Properties of the HA codon-mutant library as assessed by Sanger sequencing of 34 individual clones drawn roughly evenly from the three experimental replicates.
(A) There are an average of 2.1 codon mutations per clone, with the number per clone following a roughly Poisson distribution. (B) The codon mutations involve a mix of one-, two-, and three-nucleotide mutations. (C) The nucleotide composition of the mutant codons is roughly uniform. (D) The mutations are distributed uniformly along HA's primary sequence. (E) There is no tendency for mutations to cluster in primary sequence. Shown is distribution of observed pairwise distances between mutations in multiply mutated clones vs the expected distribution when the mutations are placed independently in the clones. All plots show results only for substitution mutations; insertion/deletion mutations are not shown. However, only two insertion/deletion mutations (0.06 per clone) were identified. The data and computer code used to generate this figure are at https://github.com/jbloom/SangerMutantLibraryAnalysis/tree/v0.2.
Figure 3 with 3 supplements
The per-codon frequencies of mutations in the samples.
The samples are named as in Figure 1, with the experimental replicate indicated with the numeric label. The DNA samples have a low frequency of mutations, and these mutations are composed almost entirely of single-nucleotide codon changes—these samples quantify the baseline error rate from PCR and deep sequencing. The mutation frequency is only slightly elevated in virus samples, indicating that viral replication and reverse transcription introduce only a small number of additional mutations. The mutDNA samples have a high frequency of single- and multi-nucleotide codon mutations, as expected from the codon mutagenesis procedure. The mutvirus samples have a lower mutation frequency, with most of the reduction due to fewer stop-codon and nonsynonymous mutations—consistent with purifying selection purging deleterious mutations. The data and code used to create this plot is available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html; this plot is the file parsesummary_codon_types_and_nmuts.pdf described therein. The sequencing accuracy was increased by using overlapping paired-end reads as illustrated in Figure 3—figure supplement 1. The overall number of overlapping paired-end reads for each sample is shown in Figure 3—figure supplement 2. A representative plot of the read depth across the primary sequence is shown in Figure 3—figure supplement 3.
Figure 3—figure supplement 1
The overlapping paired-end Illumina sequencing strategy.
(A) Sequencing accuracy was increased by fragmenting the HA gene to pieces roughly 50 nucleotides in length, and then using overlapping paired-end 50 nucleotide Illumina sequencing reads. Codon identities were only called if the reads overlapped and concurred on the codon identity. (B) The distribution of actual HA fragment lengths for a representative sample. The plot in (B) is the file replicate_3/DNA/replicate_3_DNA_insertlengths.pdf described at http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
Figure 3—figure supplement 2
The total number of reads for each sample.
For all samples, the majority of reads could be paired and aligned to the HA sequence. However, the exact fraction of reads that could be paired varied somewhat among samples due to variation in the efficiency with which the HA gene was fragmented to the target length of 50 nucleotides. This plot is the file alignmentsummaryplot.pdf described at http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
Figure 3—figure supplement 3
The per-codon read depth as a function of primary sequence.
This plot is typical of the samples. The read depth varied fairly consistently as a function of primary sequence, presumably due to biases in the positions at which the HA gene tended to fragment. This plot is the file replicate_3/DNA/replicate_3_DNA_codondepth.pdf described at http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
Figure 4 with 1 supplement
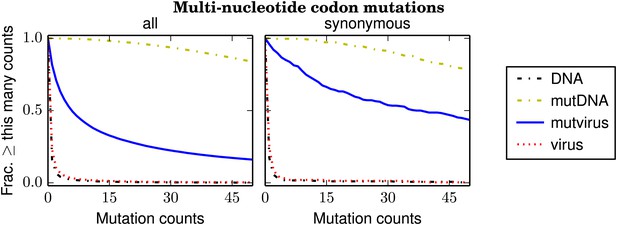
The number of times that each possible multi-nucleotide codon mutation was observed in each sample after combining the data for the three biological replicates.
Nearly all mutations were observed many times in the mutDNA samples, indicating that the codon mutagenesis was comprehensive. Only about half of the mutations were observed at least five times in the mutvirus samples, indicating either a bottleneck during virus generation or purifying selection against many of the mutations. If the analysis is restricted to synonymous multi-nucleotide codon mutations, then about 85% of mutations are observed at least five times in the mutvirus samples. Since synonymous mutations are less likely to be eliminated by purifying selection, this latter number provides a lower bound on the fraction of codon mutations that were sampled by the mutant viruses. The redundancy of the genetic code means that the fraction of amino-acid mutations sampled is higher. The data and code used to create this figure are available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html; this plot is the file countparsedmuts_multi-nt-codonmutcounts.pdf described therein. Similar plots for the individual replicates are shown in Figure 4—figure supplement 1.
Figure 4—figure supplement 1
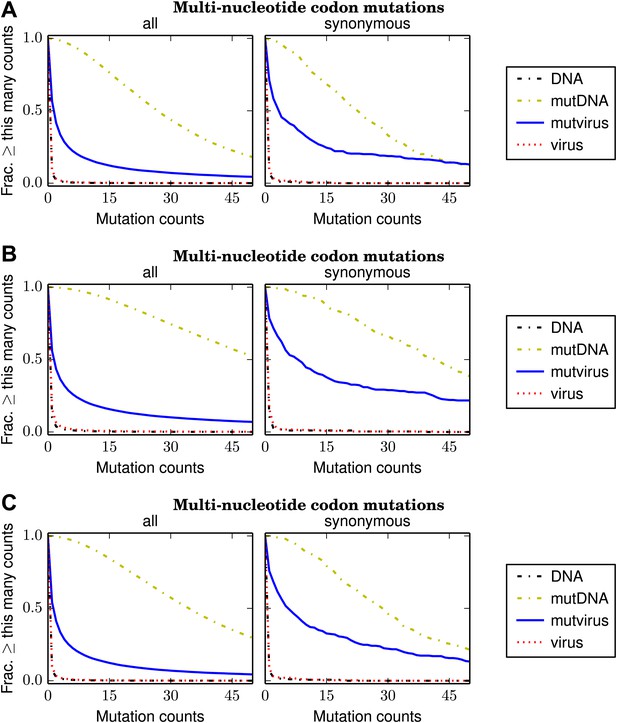
Plots like those in Figure 4 for the individual biological replicates.
(A) replicate 1, (B) replicate 2, and (C) replicate 3. These plots are the files replicate_1/countparsedmuts_multi-nt-codonmutcounts.pdf, replicate_2/countparsedmuts_multi-nt-codonmutcounts.pdf, and replicate_3/countparsedmuts_multi-nt-codonmutcounts.pdf described at http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
Figure 5 with 1 supplement
The amino-acid preferences inferred using the combined data from the three biological replicates.
The letters have heights proportional to the preference for that amino acid, and are colored by hydrophobicity. The first overlay bar shows the relative solvent accessibility (RSA) for residues in the HA crystal structure. The second overlay bar indicates Caton et al. antigenic sites or conserved receptor-binding residues. The sequence is numbered sequentially beginning with 1 at the N-terminal methionine—however, this first methionine is not shown as it was not mutagenized. Figure 5—figure supplement 1 shows the same data with H3 numbering of the sequence. The data and code used to create this figure are available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html; this plot is the file sequentialnumbering_site_preferences_logoplot.pdf described therein.
Figure 5—figure supplement 1
A plot matching that shown in Figure 5 except that the HA sequence is numbered using the H3 numbering scheme.
This plot is the file H3numbering_site_preferences_logoplot.pdf described at http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
Figure 6
Correlations among the amino-acid preferences inferred using data from the individual biological replicates.
(A) The preferences from two technical repeats of the sample preparation and deep sequencing of biological replicate #1 are highly correlated. (B)–(D) The preferences from the three biological replicates are substantially but imperfectly correlated. Overall, these results indicate that technical variation in sample preparation and sequencing is minimal, but that there is substantial variation between biological replicates due to stochastic differences in which mutant viruses predominate during the initial reverse-genetics step. The Pearson correlation coefficient (R) and associated p-value are shown in the upper-left corner of each plot. The data and code used to create this figure are available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html; these plots are the files correlations/replicate_1_vs_replicate_1_repeat.pdf, correlations/replicate_1_vs_replicate_2.pdf, correlations/replicate_1_vs_replicate_3.pdf, and correlations/replicate_2_vs_replicate_3.pdf described therein.
Figure 7
Correlation of the site-specific amino-acid preferences determined in our study with the “relative fitness” (RF) values reported by Wu et al. (2014). Wu et al. (2014) report RF values for 2350 of the 564×19 = 10716 possible amino-acid mutations to the WSN HA examined in our study (they only examine single-nucleotide changes and disregard certain types of mutations due to oxidative damage of their DNA).
To compare across the data sets, we have normalized their RF values by the RF value for the wildtype amino-acid (which they provide for only 2264 of the 2350 mutations). We then correlate on a logarithmic scale these normalized RF values with the ratio of our measurement of the preference for the mutant amino acid divided by the preference for the wildtype amino acid, using the preferences from our combined replicates. For mutations for which Wu et al. (2014) report an RF of zero, we assign a normalized RF equal to the smallest value for their entire data set. There is a significant Pearson correlation of 0.48 between the data sets, indicating that both our experiments and those of Wu et al. (2014) are capturing many of the same constraints on HA. The data and code used to create this figure are available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html; this plot is the file correlation_with_Wu_et_al.pdf described therein.
Figure 8 with 1 supplement
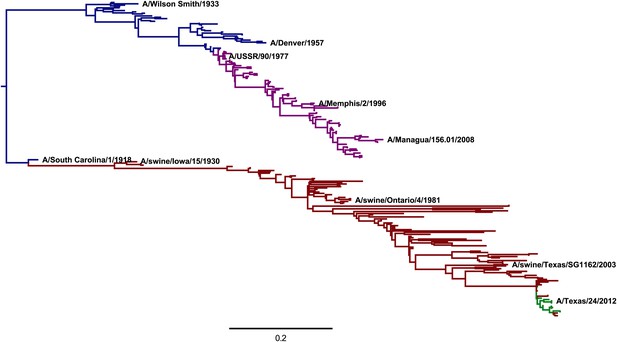
A phylogenetic tree of human and swine H1 HA sequences descended from a common ancestor closely related to the 1918 virus.
The WSN virus used in the experiments here is a lab-adapted version of the A/Wilson Smith/1933 strain. Human H1N1 that circulated from 1918 until 1957 is shown in blue. Human seasonal H1N1 that reappeared in 1977 is shown in purple. Swine H1N1 is shown in red. The 2009 pandemic H1N1 is shown in green. This tree was constructed using codonPhyML (Gil et al., 2013) with the substitution model of Goldman and Yang (1994). This plot is the file CodonPhyML_Tree_H1_HumanSwine_GY94/annotated_tree.pdf described at http://jbloom.github.io/phyloExpCM/example_2014Analysis_Influenza_H1_HA.html. Figure 8—figure supplement 1 shows a tree estimated for the same sequences using the substitution model of Kosiol et al. (2007).
Figure 8—figure supplement 1
A phylogenetic tree of the same sequences shown in Figure 8, this time inferred using the substitution model of Kosiol et al. (2007).
This tree is extremely similar to that in Figure 8, indicating the inferred topology is robust to the exact choice of codon-substitution model. This plot is the file CodonPhyML_Tree_H1_HumanSwine_KOSI07/annotated_tree.pdf described at http://jbloom.github.io/phyloExpCM/example_2014Analysis_Influenza_H1_HA.html.
Figure 9
The frequencies of amino acids among the naturally occurring HA sequences in Figure 8 vs the amino-acid preferences inferred from the combined replicates (Figure 5).
Note that a natural frequency close to one or zero could indicate absolute selection for or against a specific amino acid, but could also simply result from the fact that natural evolution has not completely sampled all possible mutations compatible with HA structure and function. The Pearson correlation coefficient (R) and associated p-value are shown on the plot. This plot is the file natural_frequency_vs_preference.pdf described at http://jbloom.github.io/phyloExpCM/example_2014Analysis_Influenza_H1_HA.html.
Figure 10
Inherent mutational tolerance of HA’s receptor-binding residues and antigenic sites.
(A) Surface of HA with one monomer colored by site entropy as determined by the deep mutational scanning; blue indicates low mutational tolerance and red indicates high mutational tolerance. (B) The structure shows residues classified as antigenic sites by Caton et al. (1982) in colored spheres; the plot shows site entropy vs relative solvent accessibility (RSA) of these residues (red triangles) and all other HA1 residues in the crystal structure (blue circles). (C) Antigenic sites of Caton et al. (1982) plus all other surface-exposed residues that contact these sites. (D) Conserved receptor-binding residues. (E) All receptor-binding residues. Table 4 shows that residues in (B) and (C) have unusually high mutational tolerance, residues in (D) have unusually low mutational tolerance, and residues in (E) do not have unusual mutational tolerance. The data and code to create all panels of this figure is provided via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html. The structure is PDB 1RVX (Gamblin et al., 2004).
Figure 11
The inherent mutational tolerance of NP's CTL epitopes is indistinguishable from that of non-epitope sites in NP.
The plot shows the site entropy vs relative solvent accessibility (RSA) of NP residues that participate in multiple CTL epitopes (red triangles) and all other NP residues in the crystal structure (blue circles). Visual inspection suggests that the epitope sites have mutational tolerance comparable to other sites, and this result is supported by the statistical analysis in Table 5. Note that unlike for HA, there is no trend for RSA to correlate with site entropy—this could be because many of NP’s surface-exposed sites are constrained by interactions with viral RNA. The CTL epitopes are those delineated in the first supplementary table of Gong and Bloom (2014). The site entropies are computed from a previously described deep mutational scan of NP, and are the values in the first supplementary file of Bloom (2014); the RSA values are also taken from that reference. The data and code used to generate this plot is available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html; the plot itself is the file NP_CTL_entropy_rsa_correlation.pdf described therein.
Tables
Table 1
The amino-acid preferences inferred from the combined experimental replicates are consistent with existing knowledge about HA structure and function
| Site in sequential numbering | Site in H3 numbering | Existing knowledge | Inferred amino-acid preferences |
|---|---|---|---|
| 127 | 117 (HA1) | Mutation from S to P creates a temperature-sensitive defect (Nakajima et al., 1986) | The preference for S is 30 times higher than the preference for P |
| 174 | 161 (HA1) | Mutation from Y to H creates a temperature-sensitive defect (Nakajima et al., 1986) | The preference for Y is 25 times higher than the preference for H |
| 344 | 1 (HA2) | Mutation from G to E abolishes HA fusion activity (Qiao et al., 1999) | The preference for G is 11 times higher than for E |
| 343 | 327 (HA1) | A basic residue (R or K) is required for HA proteolytic activation (Stech et al., 2005) | The combined preferences for R and K (0.87) far exceed those of all other amino acids combined |
| 108 | 98 (HA1) | Receptor-binding residue, is Y in >99% of natural H1 HAs | The preference for Y (0.61) exceeds those of all other amino acids combined |
| 166 | 153 (HA1) | Receptor-binding residue, is W in >99% of natural H1 HAs | The preference for W (0.65) exceeds those of all other amino acids combined |
| 196 | 183 (HA1) | Receptor-binding residue, is H in >99% of natural H1 HAs | The preference for H (0.69) exceeds those of all other amino acids combined |
| 203 | 190 (HA1) | Receptor-binding residue, is D in 90% of natural H1 HAs | The highest preference is for the chemically similar E |
| 207 | 194 (HA1) | Receptor-binding residue, is L in 97% of natural H1 HAs | The preference for L (0.55) exceeds those of all other amino acids combined |
| 208 | 195 (HA1) | Receptor-binding residue, is Y in >99% of natural H1 HAs | The preference for Y (0.72) exceeds those of all other amino acids combined |
| 239 | 226 (HA1) | Receptor-binding residue, is Q in ≈99% of natural H1 HAs | Q is one of three amino acids with a high preference |
| 241 | 228 (HA1) | Receptor-binding residue, is G in >99% of natural H1 HAs | The preference for G (0.57) exceeds those of all other amino acids combined |
-
The conserved receptor-binding residues listed in this table are those delineated in the first table of Martin et al. (1998) that also have at least 90% conservation among all naturally occurring H1 HAs in the Influenza Virus Resource (Bao et al., 2008).
Table 2
An evolutionary model derived from the experimentally inferred amino-acid preferences describes the HA sequence phylogeny in Figure 8 far better than a variety of existing state-of-the-art models
| Model | Δ AIC | Log likelihood | Parameters (optimized + empirical) |
|---|---|---|---|
| Combined | 0.0 | −24088.7 | 0 (0 + 0) |
| replicate 3 | 303.2 | −24240.3 | 0 (0 + 0) |
| Combined, Halpern and Bruno | 500.6 | −24339.0 | 0 (0 + 0) |
| replicate 1 | 535.4 | −24356.4 | 0 (0 + 0) |
| replicate 3, Halpern and Bruno | 657.8 | −24417.6 | 0 (0 + 0) |
| replicate 2 | 876.2 | −24526.8 | 0 (0 + 0) |
| GY94, gamma ω, gamma rates | 882.6 | −24517.0 | 13 (4 + 9) |
| replicate 1, Halpern and Bruno | 983.2 | −24580.3 | 0 (0 + 0) |
| GY94, gamma ω, one rate | 1109.7 | −24631.5 | 12 (3 + 9) |
| replicate 2, Halpern and Bruno | 1190.0 | −24683.7 | 0 (0 + 0) |
| KOSI07, gamma ω, gamma rates | 1620.5 | −24834.9 | 64 (4 + 60) |
| GY94, one ω, gamma rates | 1859.4 | −25006.4 | 12 (3 + 9) |
| KOSI07, gamma ω, one rate | 1883.0 | −24967.2 | 63 (3 + 60) |
| KOSI07, one ω, gamma rates | 2378.8 | −25215.1 | 63 (3 + 60) |
| GY94, one ω, one rate | 2544.5 | −25350.0 | 11 (2 + 9) |
| KOSI07, one ω, one rate | 3040.0 | −25546.7 | 62 (2 + 60) |
| combined, randomized | 5632.8 | −26905.1 | 0 (0 + 0) |
| replicate 1, randomized | 6002.4 | −27089.9 | 0 (0 + 0) |
| replicate 3, randomized | 6138.8 | −27158.1 | 0 (0 + 0) |
| replicate 2, randomized | 6477.8 | −27327.6 | 0 (0 + 0) |
| combined, randomized, Halpern and Bruno | 7072.8 | −27625.1 | 0 (0 + 0) |
| replicate 1, randomized, Halpern and Bruno | 7795.0 | −27986.2 | 0 (0 + 0) |
| replicate 3, randomized, Halpern and Bruno | 7891.8 | −28034.6 | 0 (0 + 0) |
| replicate 2, randomized, Halpern and Bruno | 8494.4 | −28335.9 | 0 (0 + 0) |
-
The model is most accurate if it utilizes data from the combined experimental replicates, but it also outperforms existing models even if the data are only derived from individual replicates. Models are ranked by AIC (Posada and Buckley, 2004). GY94 indicates the model of Goldman and Yang (1994), and KOSI07 indicates the model of Kosiol et al. (2007). The nonsynonymous/synonymous ratio (ω) and the substitution rate are either estimated as a single value or drawn from a four-category gamma distribution. Randomizing the experimentally inferred preferences among sites makes the models far worse. The models work best fixation probabilities are computed from the preferences using the first equation proposed in Bloom (2014). The table also shows the results if the fixation probabilities are instead computed using the equation of Halpern and Bruno (1998) as described in Bloom (2014). This table is the file H1_HumanSwine_GY94_summary.tex described at http://jbloom.github.io/phyloExpCM/example_2014Analysis_Influenza_H1_HA.html. Table 3 shows the results when the tree topology is instead estimated using the substitution model of Kosiol et al. (2007).
Table 3
An evolutionary model derived from the experimentally inferred amino-acid preferences also outperforms existing models for the tree topology in Figure 8—figure supplement 1
| Model | ΔAIC | Log likelihood | Parameters (optimized + empirical) |
|---|---|---|---|
| Combined | 0.0 | −24082.5 | 0 (0 + 0) |
| replicate 3 | 304.8 | −24234.9 | 0 (0 + 0) |
| Combined, Halpern and Bruno | 494.4 | −24329.7 | 0 (0 + 0) |
| replicate 1 | 534.2 | −24349.6 | 0 (0 + 0) |
| replicate 3, Halpern and Bruno | 653.2 | −24409.1 | 0 (0 + 0) |
| replicate 2 | 869.4 | −24517.2 | 0 (0 + 0) |
| GY94, gamma ω, gamma rates | 876.7 | −24507.8 | 13 (4 + 9) |
| replicate 1, Halpern and Bruno | 976.8 | −24570.9 | 0 (0 + 0) |
| GY94, gamma ω, one rate | 1101.0 | −24621.0 | 12 (3 + 9) |
| replicate 2, Halpern and Bruno | 1180.4 | −24672.7 | 0 (0 + 0) |
| KOSI07, gamma ω, gamma rates | 1609.0 | −24823.0 | 64 (4 + 60) |
| GY94, one ω, gamma rates | 1856.2 | −24998.6 | 12 (3 + 9) |
| KOSI07, gamma ω, one rate | 1867.3 | −24953.1 | 63 (3 + 60) |
| KOSI07, one ω, gamma rates | 2367.9 | −25203.4 | 63 (3 + 60) |
| GY94, one ω, one rate | 2548.3 | −25345.6 | 11 (2 + 9) |
| KOSI07, one ω, one rate | 3028.0 | −25534.5 | 62 (2 + 60) |
| Combined, randomized | 5628.0 | −26896.5 | 0 (0 + 0) |
| replicate 1, randomized | 5993.6 | −27079.3 | 0 (0 + 0) |
| replicate 3, randomized | 6138.0 | −27151.5 | 0 (0 + 0) |
| replicate 2, randomized | 6475.2 | −27320.1 | 0 (0 + 0) |
| combined, randomized, Halpern and Bruno | 7069.4 | −27617.2 | 0 (0 + 0) |
| replicate 1, randomized, Halpern and Bruno | 7786.8 | −27975.9 | 0 (0 + 0) |
| replicate 3, randomized, Halpern and Bruno | 7889.2 | −28027.1 | 0 (0 + 0) |
| replicate 2, randomized, Halpern and Bruno | 8496.0 | −28330.5 | 0 (0 + 0) |
-
This table differs from Table 2 in that it uses the tree topology inferred with the model of Kosiol et al. (2007) rather than Goldman and Yang (1994). This table is the file H1_HumanSwine_KOSI07_summary.tex described at http://jbloom.github.io/phyloExpCM/example_2014Analysis_Influenza_H1_HA.html.
Table 4
The antigenic sites are more significantly mutationally tolerant than other HA1 residues with similar relative solvent accessibility (RSA), the conserved receptor-binding residues are significantly less mutationally tolerant than other similar residues, and sites in the more expansive set of all receptor-binding residues have typical levels of mutational tolerance
| Model: site entropy ∼ RSA + (Caton et al. antigenic site) + intercept | |||
| Property | Estimate | Standard error | p-value |
| RSA | 1.29 | 0.12 | <10−10 |
| Caton et al. antigenic site | 0.30 | 0.09 | 1.6 × 10−3 |
| Model: site entropy ∼ RSA + (antigenic site or contacting residue) + intercept | |||
| Property | Estimate | Standard error | p-value |
| RSA | 1.22 | 0.13 | <10−10 |
| antigenic site or contacting residue | 0.23 | 0.07 | 2.2 × 10−3 |
| Model: site entropy ∼ RSA + (conserved receptor binding) + intercept | |||
| Property | Estimate | Standard error | p-value |
| RSA | 1.38 | 0.11 | <10−10 |
| conserved receptor binding | −0.52 | 0.16 | 1.7 × 10−3 |
| Model: site entropy ∼ RSA + (all receptor binding) + intercept | |||
| Property | Estimate | Standard error | p-value |
| RSA | 1.40 | 0.11 | <10−10 |
| all receptor binding | −0.18 | 0.11 | 0.12 |
-
The sets of residues analyzed here are those shown in Figure 10. Shown here are the results of multiple linear regression of the continuous dependent variable of site entropy (as computed from the amino-acid preferences) vs the continuous independent variable of RSA and the binary variable of being a receptor-binding residue or being an antigenic site. The data and code used to perform these analyses are available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
Table 5
There is no statistically significant difference between the inherent mutational tolerance of NP sites involved in multiple CTL epitopes and all other NP residues
| Model: NP site entropy ∼ RSA + (multiple CTL epitopes) + intercept | |||
|---|---|---|---|
| Property | Estimate | Standard error | p-value |
| RSA | −0.05 | 0.07 | 0.52 |
| multiple CTL epitopes | −0.04 | 0.04 | 0.31 |
-
The table shows the result of multiple linear regression of the continuous dependent variable of site entropy (as computed from the amino-acid preferences) vs the continuous independent variable of RSA and the binary variable of participating in multiple CTL epitopes. The data set analyzed here is plotted in Figure 11. The data and code used to perform this analysis are available via http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
Additional files
-
Supplementary file 1
The coding sequence of the WSN HA gene used in this study is provided in FASTA format.
- https://doi.org/10.7554/eLife.03300.025
-
Supplementary file 2
An Excel file listing the oligonucleotides used for the codon mutagenesis.
- https://doi.org/10.7554/eLife.03300.026
-
Supplementary file 3
The site-specific amino-acid preferences as computed from the averages of the three unique replicates are provided in this supplementary file in text format. This is the file combined_equilibriumpreferences.txt described at http://jbloom.github.io/mapmuts/example_WSN_HA_2014Analysis.html.
- https://doi.org/10.7554/eLife.03300.027
-
Supplementary file 4
The alignment of human and swine HA sequences used to build the phylogenetic trees are provided in this supplementary file in FASTA format. This is the file H1_HumanSwine_alignment.fasta described at http://jbloom.github.io/phyloExpCM/example_2014Analysis_Influenza_H1_HA.html.
- https://doi.org/10.7554/eLife.03300.028
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The inherent mutational tolerance and antigenic evolvability of influenza hemagglutinin
eLife 3:e03300.
https://doi.org/10.7554/eLife.03300
