Quantitative determinants of aerobic glycolysis identify flux through the enzyme GAPDH as a limiting step
- Cornell University, United States
- Harvard Medical School, United States
- Johns Hopkins University School of Medicine, United States
Figures
Figure 1
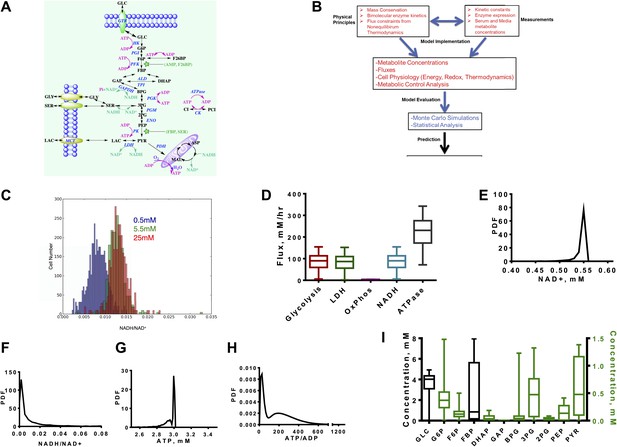
A quantitative model and statistical simulation method captures the diversity of metabolic states observed in tumor and proliferating cells.
(A) Schematic of the glycolysis model with chemical reactions and allosteric points of regulation described. Abbreviations: GLC—glucose, G6P—glucose-6-phosphate, F6P—fructose-6-phosphate, FBP—fructose-1,6,-bisphosphate, F26BP—fructose-2,6,-bisphosphate, GAP—glcyceraldehyde-3-phosphate, DHAP—dihydroxyacetone phosphate, BPG—1,3 bisphosphoglycerate, 3PG—3-phosphoglycerate, 2PG—2-phosphoglycerate, PEP—phosphoenolpyruvate, PYR—pyruvate, SER—Serine, GLY—glycine, Lac—lactate, MAL—malate, ASP—aspartate, Pi—inorganic phosphate, CI—creatine, PCI—phosphophocreatine, GTR—glucose transporter, HK—hexokinase, PGI—phosphoglucoisomerase, PFK—phosphofructokinase, ALD—aldolase, TPI—triosephosphoisomerase, GAPDH—glyceraldehyde-phosphate dehydrogenase, PGK—phosphoglycerate kinase, PGM—phosphoglycerate mutase, ENO—enolase, PK—pyruvate kinase, LDH—lactate dehydrogenase, MCT—monocarboxylate transporter, PDH—pyruvate dehydrogenase, CK—creatine kinase. (B) Overview of the algorithm and simulation method. (C) Measured values of the NADH/NAD+ ratio across a population of MCF10A breast epithelial cells. Three values of glucose concentration are considered (0.5 mM blue, 5.5 mM green, and 25 mM red). (D) Calculated fluxes (mM/hr) for glycolysis rate (Glycolysis) are defined as the rate of glucose to pyruvate (per molecule of pyruvate), pyruvate to lactate flux (LDH), rate of oxygen consumption (OxPhos), rate of NADH turnover (NADH), and ATP turnover (ATPase). (E) Calculated probability density function (PDF) of NAD+ concentrations. (F) Calculated probability density function (PDF) of NADH/NAD+ ratio. (G) Calculated probability density function (PDF) of ATP concentrations. (H) Calculated probability density function (PDF) of ATP/ADP ratio. (I) Box plots showing the distribution of concentrations computed from the simulation for each intermediate in glycolysis.
Figure 2
Evaluation of the statistics of the Warburg Effect and relationships to other variables in metabolism.
(A) Probability density function (PDF) of the Warburg Effect (WE) defined as the ratio of flux through LDH to that of flux into the mitochondria. (B) Pearson correlations of intermediate metabolite levels in glycolysis with the extent of the Warburg Effect (WE). (C) Pearson correlations of the expression levels of glycolytic enzymes with the extent of the Warburg Effect (WE). (D) Pearson correlations of coupled metabolic parameters with the extent of the Warburg Effect (WE).
Figure 3
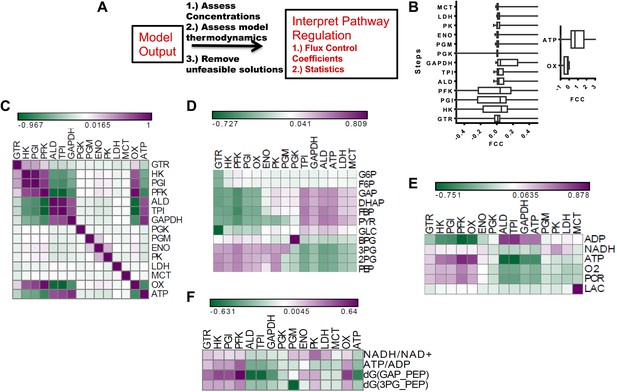
Metabolic control analysis and its relationship to metabolic variables.
(A) Schematic of workflow for global sensitivity analysis. After the model is constructed and feasible solutions obtained, each realization of glycolysis is subjected to metabolic control analysis (MCA). The resulting analysis is then subject to a statistical evaluation. (B) (left) Box plots of flux control coefficient (FCC) for lactate production for each enzymatic step in glycolysis (FCC = dlnJlac/dln Ei) where Jlac is the rate of pyruvate conversion to lactate, and Ei is the ith enzyme in glycolysis for each step of glycolysis. (right) Box plots of flux control coefficient (FCC) for lactate production for Oxygen consumption (OxPhos) and ATP consumption (ATP). (C) Pearson correlations between lactate FCC values for each step in glycolysis. Heat map is colored ranging from the minimum value (green) to the maximum value (purple). (D) Pearson correlations between metabolite concentrations in glycolysis and lactate FCC values for each step in glycolysis. Heat map is colored ranging from the minimum value (green) to the maximum value (purple). (E) Pearson correlations between metabolic parameters and lactate FCC values for each step in glycolysis. Heat map is colored ranging from the minimum value (green) to the maximum value (purple). (F) Pearson correlations between ratios and lactate FCC values for each step in glycolysis.
Figure 4
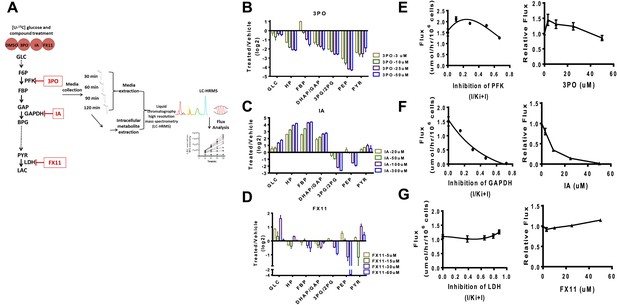
Experimental flux control coefficients.
(A) Schematic of experimental flux control analysis. Cells are pre-incubated with 13C glucose and treated with differing concentrations of inhibitors that target glycolysis at different points in the pathway. Media and intracellular metabolites are collected, subjected to (liquid chromatography high resolution mass spectrometry) LC-HRMS, and subjected to flux analysis. (B) Changes in metabolite levels observed from treatment with 3PO an inhibitor of PFK2. (C) Changes in metabolite levels observed from treatment with IA an inhibitor of GAPDH. (D) Changes in metabolite levels observed from treatment with FX11 and inhibitor of LDH. For B–D, the logarithm (log2) of the fold change of treated to vehicle across intermediates in glycolysis is shown for each concentration of compound denoted in the figure legend. Abbreviations are the same as described in Figure 1 except that HP denotes all hexose phosphates that were measured and not distinguished in the current mass spectrometry method. (E) Lactate flux from glucose as a function PFK2 inhibition. (F) Lactate flux from glucose as a function GAPDH inhibition. (G) Lactate flux from glucose as a function LDH inhibition. For E–G, the plot on the left shows the measured glucose to lactate flux as a function of the estimated fraction of enzyme inhibited (left) inhibitor concentration (right).
Figure 5
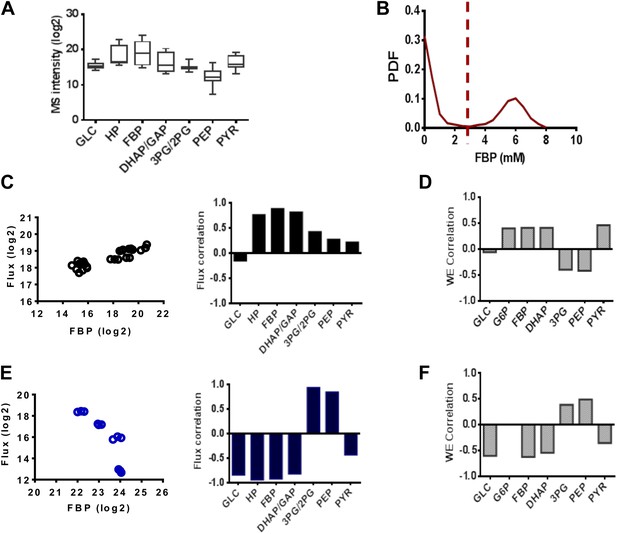
FBP levels predict distinct mechanisms in glycolysis.
(A) Variation of metabolite levels across glycolysis over 14 conditions in triplicate resulting in 42 independent experiments involving cells growing in basal conditions and those with differing extents of inhibition of glycolysis from results in Figure 4. (B) Simulated distribution of FBP levels in glycolysis. (C) Correlation of lactate flux with measured glycolytic intermediates for low FBP levels. The left panel shows data for FBP and right panel reports the values of the Spearman correlation coefficients for each metabolite. (D) Simulated correlation of lactate flux with metabolite levels of glycolytic intermediates in conditions of low FBP levels. (E) Correlation of lactate flux with measured glycolytic intermediates for high FBP levels. The left panel shows data for FBP and right panel reports the values of the Spearman correlation coefficients for each metabolite. (F) Simulated correlation of lactate flux with metabolite levels of glycolytic intermediates in conditions of low FBP levels.
Figure 6
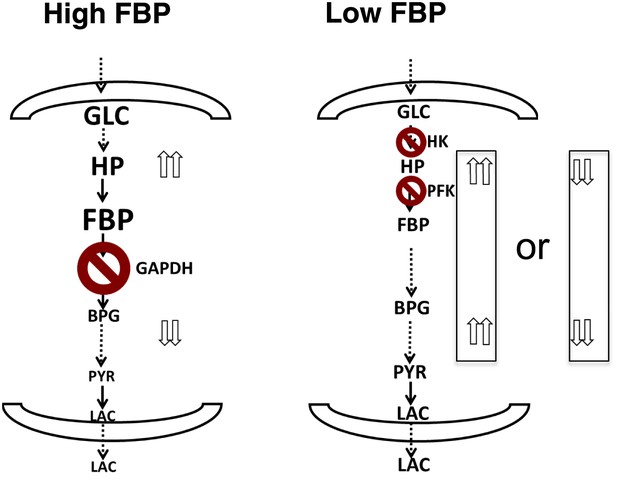
A unified model of aerobic glycolysis.
A unified picture of flux control in aerobic glycolysis. (left) Under conditions where there is an accumulation of intermediates in upper glycolysis and depletion of intermediates in lower glycolysis a bottleneck exists at the step involving GAPDH. This bottleneck is due to the status of energy and redox metabolism and the thermodynamics of the pathway that together mediate the flux through GAPDH. As a result, inhibiting flux through glycolysis is most sensitive to a perturbation in GAPDH activity. (right) Under conditions where the metabolites in glycolysis are distributed more evenly with levels together being either high or low, no such bottleneck exists. Instead flux through glycolysis leading to lactate production is most determined by the canonical pacemaking steps in glycolysis involving PFK and HK. The relative levels of glycolytic intermediates are denoted by the size of the text.
Author response image 1
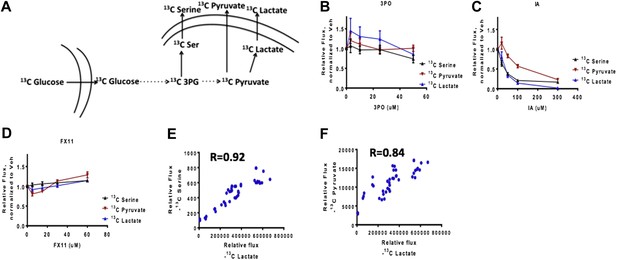
Comparison of glucose uptake rate and rate from glucose to lactate production. A) Diagram of flux experiment. Flux from glucose to pyruvate (e.g. glucose uptake), serine (biosynthetic flux), and lacate (Warburg Effect) is measured. 13C glucose is input as described in the methods. B) Comparison of fluxes for 3PO (PFK2 inhibition) treatment C) Comparison of fluxes for IA (GAPDH inhibition) treatment. D) Comparison of fluxes for FX11 (LDHA inhibition) treatment. E) Correlation between flux to serine and flux to lactate across each measurement. F) Correlation between flux to pyruvate and flux to lactate across each measurement.
Additional files
-
Supplementary file 1
Equations and parameters used for the glycolysis model.
- https://doi.org/10.7554/eLife.03342.009
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Quantitative determinants of aerobic glycolysis identify flux through the enzyme GAPDH as a limiting step
eLife 3:e03342.
https://doi.org/10.7554/eLife.03342
