Direct measurement of the mechanical work during translocation by the ribosome
- University of California, Berkeley, United States
- Technion-Israel Institute of Technology, Israel
- University of California, Santa Cruz, United States
- Howard Hughes Medical Institute, University of California, Berkeley, United States
Figures
Figure 1 with 1 supplement
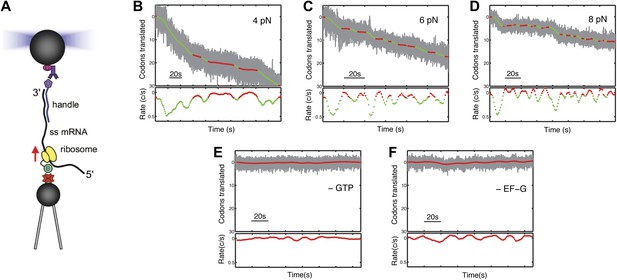
Following translation by a single ribosome on a single mRNA.
(A) Geometry for single-molecule translation experiments. A biotinylated ribosome is loaded onto a single-stranded mRNA and attached to a streptavidin-coated polystyrene bead fixed to a micropipette. The 3′ of the message is anchored to a second bead through a 1460 bp DNA/RNA hybrid handle. Calibrated forces can be applied to the ribosome by manipulating the second bead with an optical trap, while the translation progress of the ribosome is determined by the change in extension of the tether. (B–D) Typical translation events recorded under 4, 6 and 8 pN of constant tension. The upper panels show the codons translated as a function of time, and indicate that translation proceeds not in a continuous manner, but in a series of translational bursts separated by long pauses. The gray line shows the raw (1 kHz) data, while green (translocation) and red (pause) are filtered down to 1 Hz. The lower panels show the instantaneous velocities calculated from the traces above. (E and F) Control experiments, under 8 pN of tension, showing that in the absence of GTP or EF-G, no translation signals were detected.
Figure 1—figure supplement 1
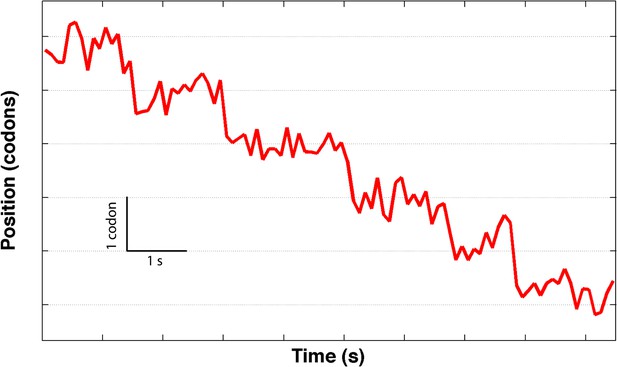
A partial translation trace showing an unusually low noise level, and a sequence of presumptive single-codon translocation steps.
The data was sampled at 2 kHz and averaged down to 5 Hz.
Figure 2
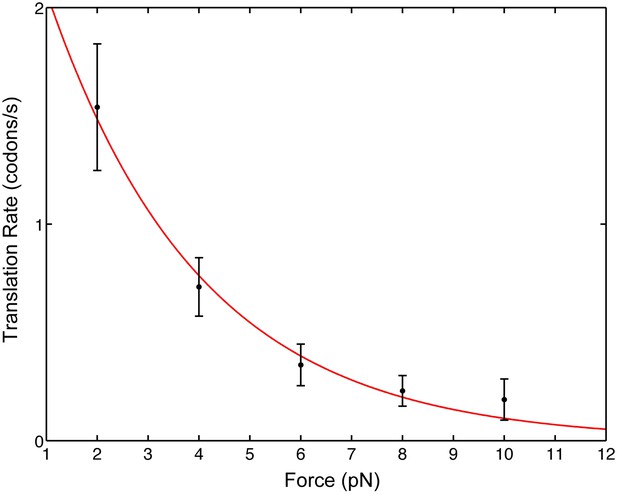
Pause-free translational velocity as a function of opposing force.
Data points are the mean velocities for all measured traces at each force (N = 54). Error bars represent the standard error of the mean. The solid line is an exponential fit of the form .
Figure 3
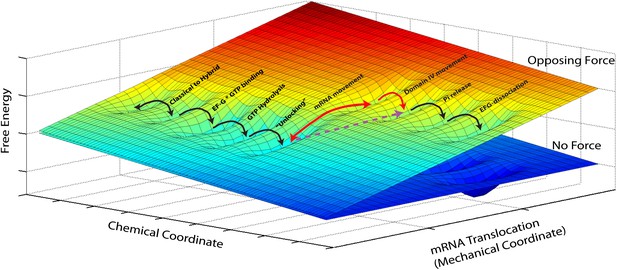
Reduced energy landscape for mRNA translocation.
The mechanical coordinate describes the movement of the mRNA relative to the 30S subunit, while the chemical coordinate describes all binding, hydrolysis and dissociation processes, in addition to conformational changes with a reaction coordinate orthogonal to the translocation coordinate probed in our experiments. Translocation proceeds by diffusive transitions between minima of this reduced energy surface. A Power Stroke mechanism involves a diagonal transition, with simultaneous progress in the chemical and mechanical axis (dashed, purple line). Alternatively, a Brownian Ratchet (full, red lines) is composed of two orthogonal transitions: a fast equilibrium between pre- and post-translocated states along the mechanical coordinated, followed by a ‘rectifying’ chemical transition.
Figure 4 with 1 supplement
Pause entry and exit rates.
(A) Pause entry rate, calculated as the inverse of the mean duration of the translation bursts in between the pauses. (B) Pause exit rate, equal to the inverse of the mean pause duration. Both rates are essentially independent of the applied opposing force.
Figure 4—figure supplement 1
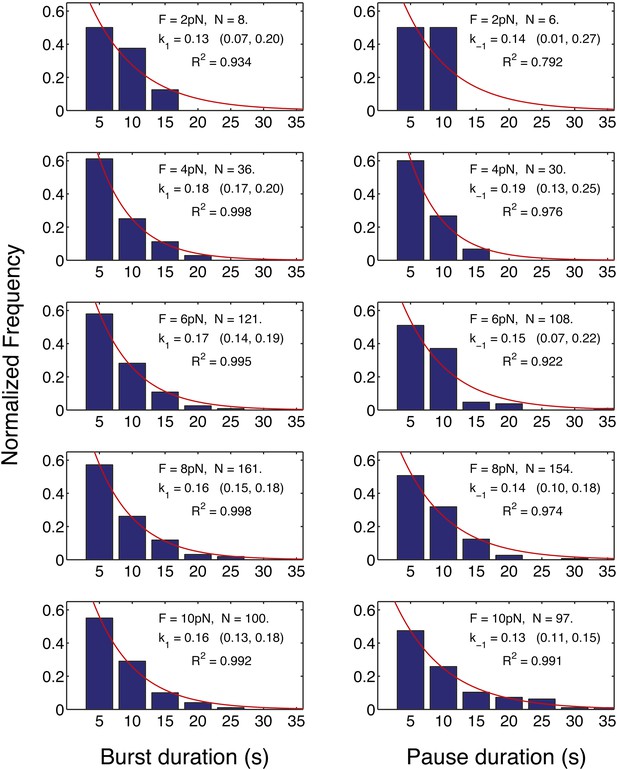
Distribution of the translation bursts and pauses durations for all the measured opposing forces.
Left panels: distribution of the bursts durations measured at the forces specified in each graph. Right panels: distributions of the pauses durations. With the exception of the pause duration distribution at 2 pN, for which the amount of data is limited (N = 6), all the distributions are well fitted by a single exponential function. The rates calculated from the distributions (k1, k−1) are indicated together with their 95% confidence interval. These rates are in good agreement with the rates calculated from the mean burst and mean pause durations (Figure 4).
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Direct measurement of the mechanical work during translocation by the ribosome
eLife 3:e03406.
https://doi.org/10.7554/eLife.03406
