Perturbation biology nominates upstream–downstream drug combinations in RAF inhibitor resistant melanoma cells
- Memorial Sloan Kettering Cancer Center, United States
- Tri-Institutional Training Program in Computational Biology and Medicine, United States
- The Sidney Kimmel Comprehensive Cancer Center at Johns Hopkins University, United States
Figures
Figure 1 with 1 supplement
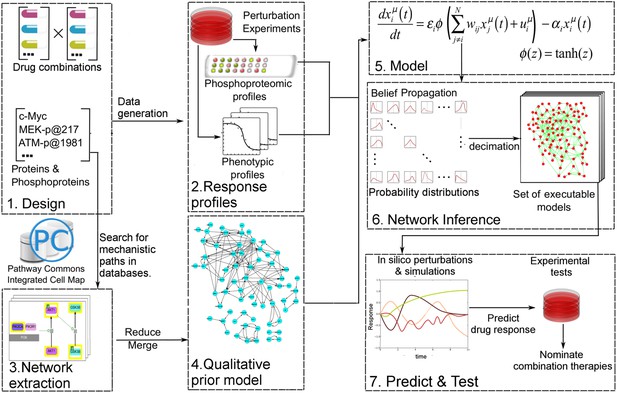
Quantitative and predictive signaling models are generated from experimental response profiles to perturbations.
Perturbation biology involves systematic perturbations of cells with combinations of targeted compounds (Box 1, 2), high-throughput measurements of responses (Box 2), automated extraction of prior signaling information from databases (Box 3, 4), construction of ordinary differential equation (ODE)-based signaling pathway models (Box 5 and Equation 1) with the belief propagation (BP) based network inference algorithm (Box 6), and prediction of system responses to novel perturbations with the models and simulations (Box 7) (Molinelli, Korkut, Wang et al., 2013). The newly developed ‘Pathway Extraction and Reduction Algorithm’ (PERA) (Box 3) generates a qualitative prior model (Box 4), which is a network of known interactions between the proteins of interest (i.e., profiled (phospho)proteins). This is achieved through a search in the Pathway Commons information resource, which integrates biological pathway information from multiple public databases. In the quantitative network models, the nodes represent measured levels of (phospho)proteins or cellular phenotypes, and the edges represent the influence of the upstream nodes on the time derivative of their downstream effectors. This definition corresponds to a simple yet efficient ODE-based mathematical description of models (Box 5). Our BP-based modeling approach combines information from the perturbation data (phosphoproteomic and phenotypic) with prior information to generate network models of signaling (Box 6). We execute the resulting ODE-based models to predict system response to untested perturbation conditions (Box 7).
Figure 1—figure supplement 1
BP-guided decimation algorithm.
The algorithm is used to construct executable, individual network model solutions from BP-generated probability distributions for each edge strength value (Wij). The algorithm chart depicts one round of BP-guided decimation to generate a single model solution. Consecutive runs of BP-guided decimation algorithm lead to construction of a network model solution ensemble.
Figure 2 with 4 supplements
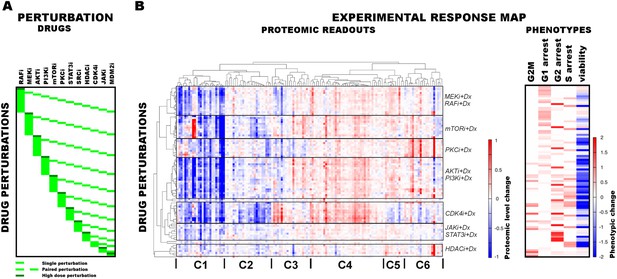
Response of melanoma cells to systematic perturbations with targeted agents.
(A) The combinatorial perturbation matrix. The melanoma cells are perturbed with combinations of targeted drugs (see Supplementary file 1C for perturbation conditions). (B) The concentration changes in 138 proteomic entities (50 phospho, 88 total protein measurements) (left) and the phenotypic changes (right) in response to drug combinations with respect to the untreated conditions form an experimental ‘response map’ of the cellular system. The response map reflects the functional relations between signaling proteins and cellular processes. The two-way clustering analysis of the proteomic readouts reveals distinct proteomic response signatures for each targeted drug. Phosphoproteomic response is measured using the RPPA technology. Cell cycle progression and viability response are measured using flow cytometry and resazurin assays, respectively. The cell cycle progression phenotype is quantified based on the percentage of the cells in a cell cycle state in perturbed condition with respect to the unperturbed condition. For the phenotypic readouts, the order of the perturbation conditions is same as in (A). The response values are relative to a no drug control and given as log2(perturbed/unperturbed).
Figure 2—figure supplement 1
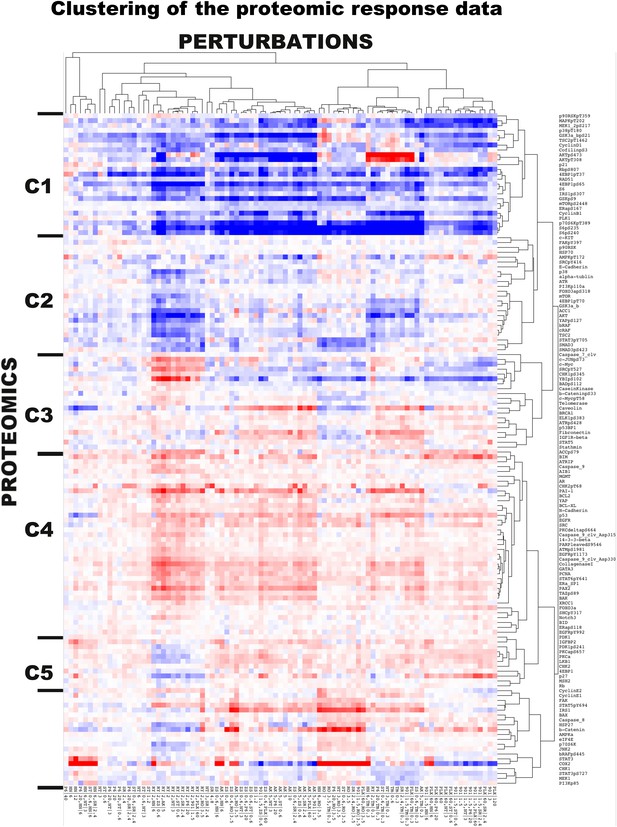
The two-way clustering analysis of the experimental response map.
The hierarchical clustering reveals distinct proteomic signatures of response to drugs targeting different signaling pathways. The Cluster software is used for the two-way hierarchical clustering with correlation-based distance metric and average-linkage method. We identified three major (C1, C2, and C4) and three minor (C3, C5, C6) proteomic response clusters.
Figure 2—figure supplement 2
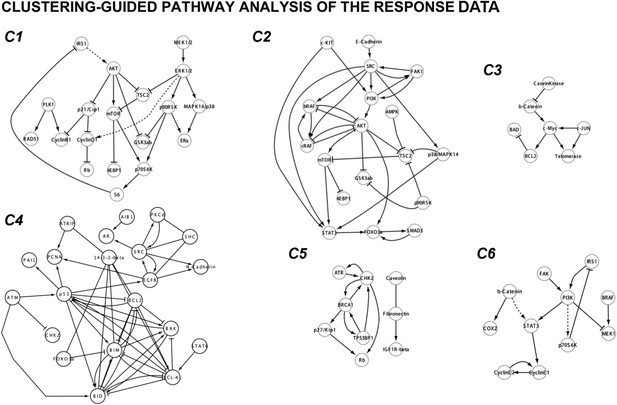
Cluster-guided pathway analysis of the response map.
We extracted the signaling interactions between the proteomic entities that fell into each cluster. The signaling interactions within each proteomic cluster are extracted from the Pathway Commons 2 database using the PERA algorithm. Here, we simplified the pathway diagrams by removing the post-translational modifications and merging the nodes associated with identical genes (e.g., AKTpT308, AKTpS473, and AKT are merged to AKT node). The resulting diagrams display the known pathways associated with proteomic response clusters. The cluster-guided pathway analysis suggests that functionally related proteins (i.e., proteins on the same or related pathways) are enriched in distinct clusters. The phospho-proteomic entities on MAPK and PI3K/AKT pathways are enriched in cluster 1 (C1) of the response map. The total protein measurements related to MAPK and PI3K/AKT pathways are enriched in a related but distinct cluster (C2). The level of various apoptotic proteins increase in response to most targeted drugs and form another distinct cluster (C4). Interestingly, EGFR (Both phospho and total level) and a set of EGFR related docking proteins (e.g., SHC, 14-3-3-β) are also enriched in C4 possibly due to the increase in the expression of those entities in response to targeted drugs such as MEKi and PI3Ki. The observed increase in EGFR level suggests a potential feedback loop that emerges from downstream elements of MAPK and PI3K/AKT pathways, which are targeted by multiple agents in this study.
Figure 2—figure supplement 3
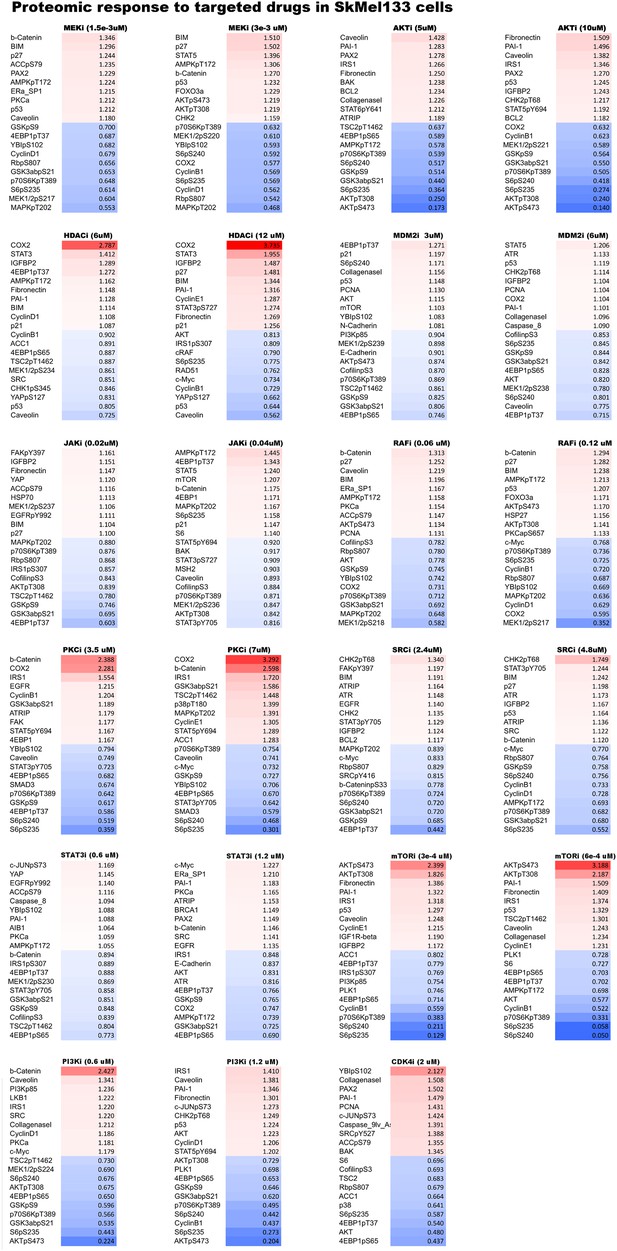
Proteomic response to single agent perturbations.
Proteomic levels in SkMel-133 cells change in response to targeted drugs as measured with reverse phase protein array (RPPA). For each drug, we listed the top 10 decreasing and increasing phosphoproteins out of 138 proteomic entities profiled with RPPA. The protein levels are normalized to no drug condition and given in linear space.
Figure 2—figure supplement 4
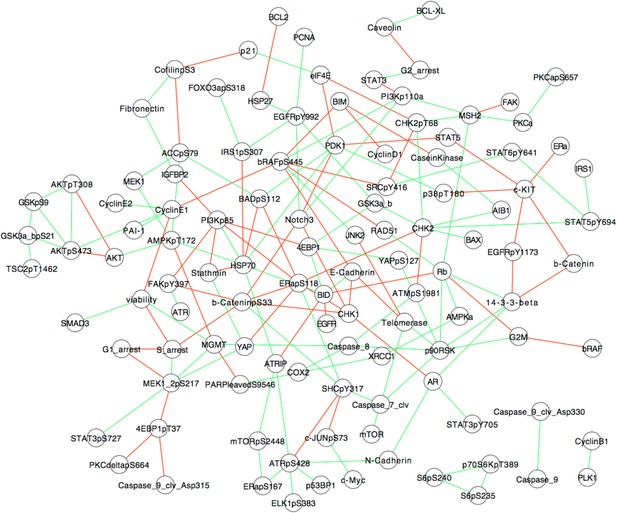
Association models of the response map from partial correlations.
A correlation-based network model of signaling is inferred using the SkMel-133 perturbation response data and the graphical Gaussian model (GGM) network inference method. GGM uses the first-order partial correlation coefficients as a measure of direct associations between two nodes, for which the effects of other nodes are eliminated. The advantage of partial correlations over the conventional pairwise correlations is its ability to distinguish direct interactions from indirect ones. Partial coefficients are calculated by inverting the correlation matrix. Here, we computed the partial correlations using the shrinkage estimation method, a form of regularized estimator of the covariance matrix and its inverse (Schafer and Strimmer, 2005). Shrinkage method is particularly useful for inferring models when number of variables is higher than number of constraints (n > p). See (Schafer and Strimmer, 2005) for algorithmic details and formulation of partial correlation calculation. The network model covers the interactions between 138 proteomic species and five phenotypic measurements (i.e., cell viability and cell cycle progression nodes). The models involve the interactions with statistically significant (False Discovery Rate (FDR) -adjusted p-value < 0.01, H0: pcor = 0 based on a null-distribution estimated from the data, see Schafer and Strimmer, 2005, for details) association strengths (green: positive, red: negative associations). The resulting models capture some of the well-characterized and potentially interesting interactions such as those between AKT, GSK3, and TSC2. Cell viability node is directly linked to proteomic nodes SMAD3, Cyclin E1, MGMT. G1-arrest node is directly linked to MEK phosphorylation node, while S-arrest is associated with beta-catenin phosphorylation node. G2-arrest is linked to STAT3 and caveolin total levels, and G2M transition is linked to BRAF, RB, and p90S6K total level nodes. The models provide an approximate picture of pairwise interactions in SkMel-133 cells, are not executable, do not capture the high-order couplings within the cellular system, and hence, we conclude that they do not have the required power for predicting system response to untested perturbations.
Figure 3 with 1 supplement
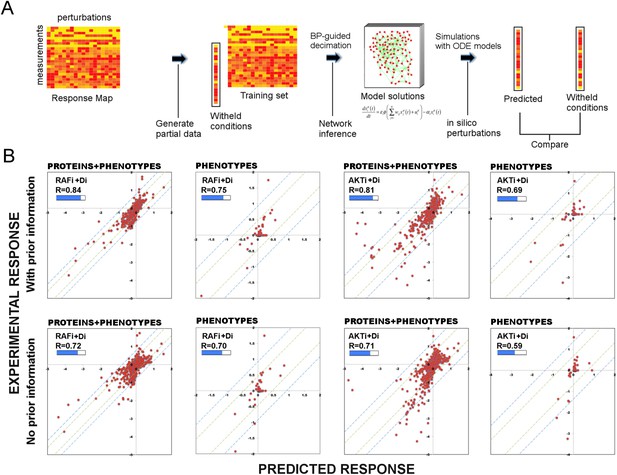
Use of prior information increases the predictive power of models.
(A) To test the predictive power of network models, a leave-11-out cross-validation test is performed. Using the BP-guided decimation algorithm, 4000 network model solutions are inferred in the presence and absence of prior information using the partial response data. Resulting models are executed with in silico perturbations to predict the withheld conditions. Each experimental data point represents the readouts from RPPA and phenotype measurements under the corresponding perturbation conditions. Each predicted data point is obtained by averaging results from simulations with in silico perturbations over 4000 model solutions. The experimental and predicted profiles are compared to demonstrate the power of network models to predict response to combinatorial drug perturbations. (B) In all conditions, network inference with prior information leads to a higher cumulative correlation coefficient (R) and significantly improved prediction quality (RAFi p = 1 × 10−3, AKTi p = 5.7 × 10−3, unpaired t-test H0: ΔXwith_prior = ΔXw/o_prior, ΔX = |Xexp − Xpred|) between experimental and predicted responses. Plots on top row: prior information is used for network inference. Plots on bottom row: no prior information is used for network inference. Response to RAFi + {Di} (first and second column) and AKTi + {Di} (third and fourth column) is withheld from the training set and the withheld response is predicted. All responses (phenotypic + proteomic) (first and third column) and only phenotypic responses (second and fourth column) are plotted. {Di} denotes set of all drug perturbations combined with drug of interest. (See Figure 3—figure supplement 1 for the cross-validation calculations with all other partial data sets and Supplementary file 1E for statistical validation of the predictions.)
Figure 3—figure supplement 1
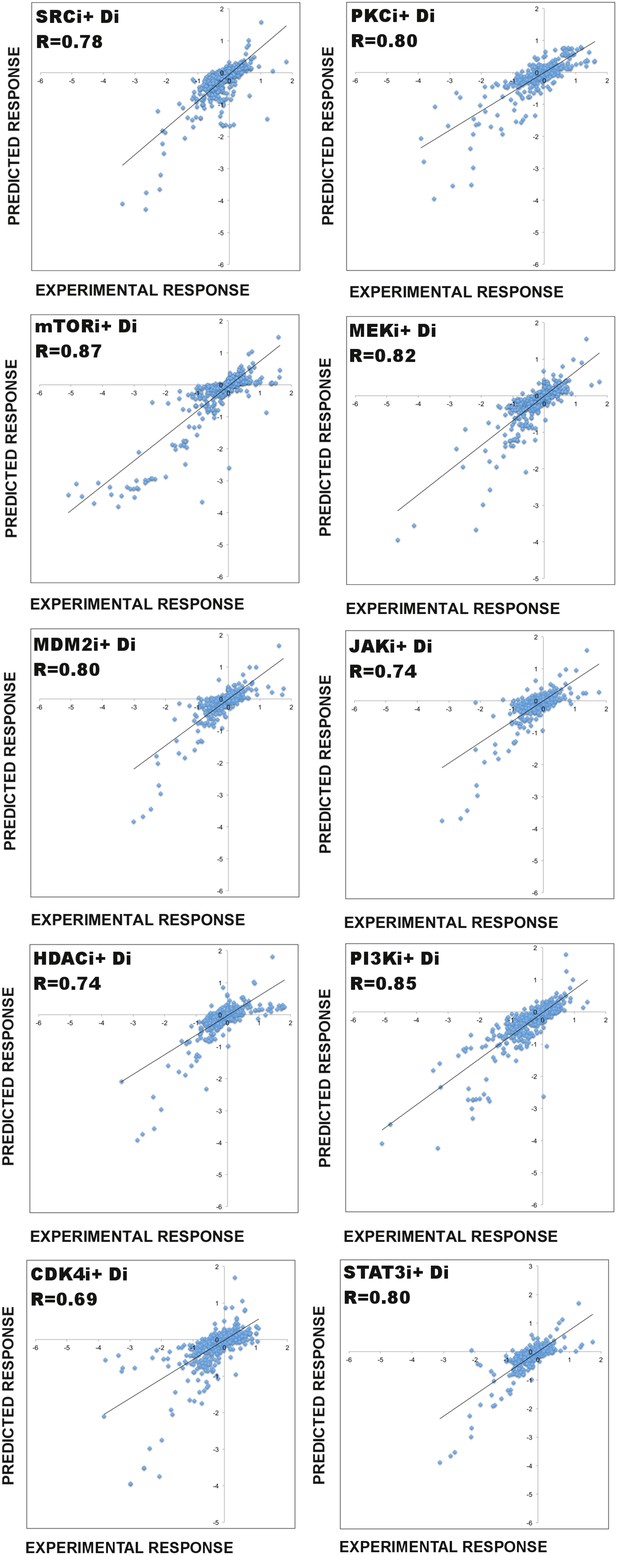
Predictive power of the perturbation biology models.
The ability of the models to predict system response to untested perturbations is tested with a leave-11-out cross-validation scheme, which involves model simulations with in silico perturbations (Figure 3A). For each cross-validation calculation, the response profile to every possible combination of an individual drug is withheld and models are constructed using the partial data (i.e., combinations of all other drugs plus the drug of interest applied as a single agent) and prior information. Through simulations of the models with in silico perturbations that represent the withheld experimental perturbations, we predict the system response in the withheld conditions. The comparison of the simulated data with the experimental data reveals the predictive power (ability of the models to predict system response to untested perturbations) of our modeling approach. Here, we demonstrate the cross-validation results for 10 drugs (see Figure 3A for RAF inhibitor [RAFi] and AKTi cross-validation results). In each plot, Di represents all drugs except the drug, for which all combinatorial drug response is withheld. For each validation calculation displayed in this figure, 1000 models are generated using the BP-guided decimation algorithm. Each model is executed with 11 in silico perturbations (e.g., mTORi + Di). The simulation results are averaged over 1000 models for each proteomic and phenotypic node and compared to the experimentally measured values. R represents the correlation between the experimental and the predicted response data. To statistically validate the predictions, we computed the frequentist coverage probability for each calculation (Supplementary file 1E).
Figure 4 with 5 supplements
Inferred network models capture oncogenic signaling pathways in melanoma.
(A) The generation of the average model. The set of <Wij> averaged over the Wij in all models provide the average network model. The signaling processes are explained through qualitative analysis of the average model and its functional subnetworks (see Figure 5 for quantitative analysis). (B) The average network model contains proteomic (white) and phenotypic nodes (orange) and the average signaling interactions (<Wij> > 0.2) over the model solutions. The edges between the BRAF, CRAF, TSC2, and AKTpT308 represent the cross-pathway interactions between the MAPK and PI3K/AKT pathways (see Figure 2—figure supplement 2 for analysis of edge distributions in the solution ensemble) (green edges: positive signed, red edges: negative signed interactions). (C) Cell cycle signaling subnetwork contains the interactions between the cyclins, CDKs, and other associated molecules (e.g., p27/Kip1). RBpS807 and cyclin D1 are the hub nodes in the subnetwork and connect multiple signaling entities. (D) ERK subnetwork. MEKpS217 is the critical hub in this pathway and links upstream BRAF and SRC to downstream effectors such as ERK phosphorylation. (E) In the PI3K/AKT subnetwork, the SRC nodes (i.e., phosphorylation, total level, activity) are upstream of PI3K and AKT (total level, AKTpS473 and AKTp308) and the AKT nodes are the major hubs. Downstream of AKT, the pathway branches to mTOR, P70S6K and S6 phosphorylation cascade and the GSK3β phosphorylation events. A negative edge originating from mTORpS2448 and acting on AKTpS473 presumably captures the well-defined negative feedback loop in the AKT pathway (O'Reilly et al., 2006). Note that nodes tagged with ‘a’ (e.g., aBRAFV600E) are activity nodes, which couple drug perturbations to proteomic changes.
Figure 4—figure supplement 1
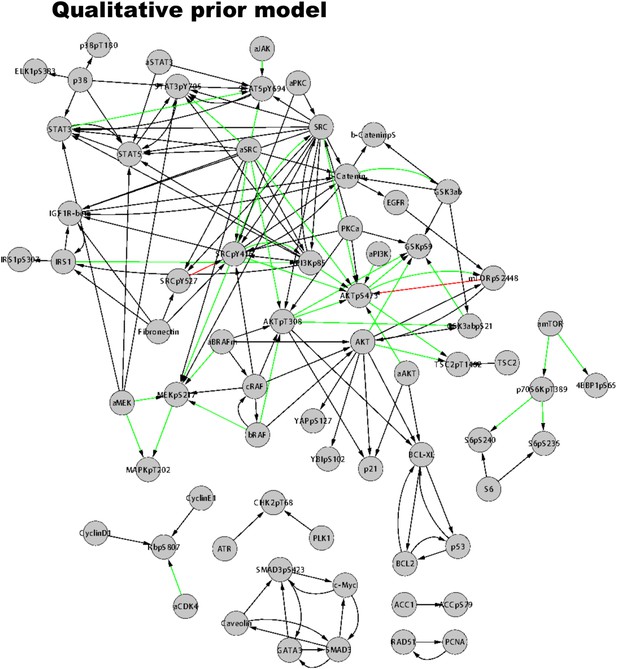
The prior model of signaling.
The prior information model is extracted from Reactome and NCI PID using the PERA algorithm (see ‘Materials and methods’ for PERA algorithm and use of the prior model in inference). The prior model served as a bias in BP-based network inference. Green arrows represent priors for activating edges, red arrows represent inhibitory edges, and black arrows represent generic edges (i.e., activating or inhibitory).
Figure 4—figure supplement 2
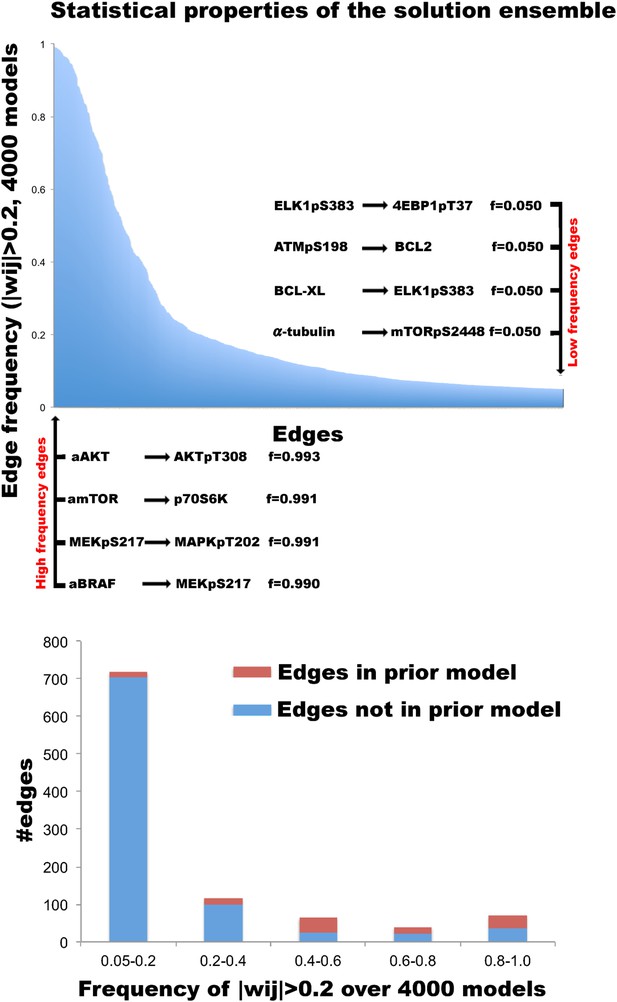
Distribution of edges in the solution ensemble.
In order to model cellular signaling and predict response, we computed 4000 signaling models and generated a solution ensemble. Top: edge frequencies (f(wij)) in the solution ensemble. The y-axis represents the frequency values for nonzero edge strengths (f(|wij| > 0.2)) in the ensemble. The X-axis represents the interactions ordered by their frequencies, f(|wij| > 0.2). The part of the long tail, which corresponds to the edges with frequencies less than 0.05, is not displayed. A set of well reported interactions such as the coupling of AKT activity node to phospho-AKT and phospho-MEK to phosho-MAPK (ERK) are inferred with |wij| > 0.2 in >99% of the model solutions (left). Few examples of the rarely captured signaling interactions are given on right. Bottom: the frequency distribution of nonzero edges (|wij| > 0.2) has a bimodal character. A set of interactions with nonzero edge values is shared by nearly all of the inferred network models (0.8 < f(|wij| > 0.2) < 1.0). Such frequent edges form a stable network skeleton shared by majority of the solutions. On the other hand, a set of possible interactions have nonzero edge strength (wij) values in ∼50% of the solutions. Such interactions vary among different model solutions and possibly account for the variations in system response predicted with different model solutions. The interactions in the prior model are particularly enriched in these two groups. A large fraction of potential interactions have very low (0.05 < f(|wij| > 0.2) < 0.20) or near zero (f(|wij| > 0.2) < 0.05) frequencies in the model ensemble.
Figure 4—figure supplement 3
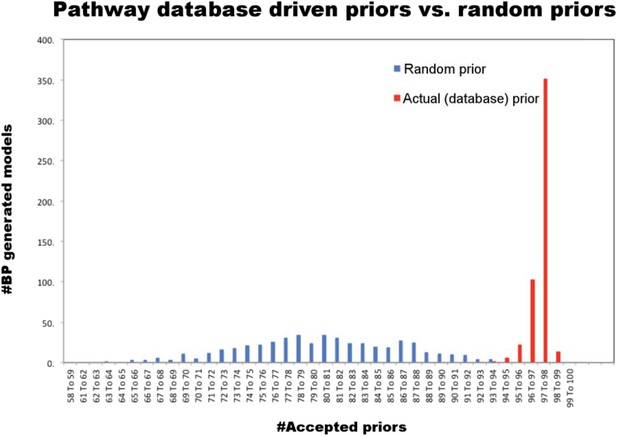
Comparison of random and actual prior information.
We tested whether the database driven prior model conforms to the experimental data and prior information does not overly restrain the inferred models. For this purpose, we constructed and compared network models using the pathway driven and randomly generated prior restraints in BP-based modeling. We have tested 500 unique, randomly generated pseudoprior restraints each containing 154 interactions, equal to the number of interactions in the pathway driven prior model. The models are generated using a fast BP-based inference method, which is different than the BP-based decimation. For model construction, we first computed the probability distribution of edge values (P(Wij)) for each possible interaction. Next, we constructed the models by assigning the edge value (Wij) for which BP-generated P(Wij) is maximum. We compared the models generated with different prior models for their prior scores (i.e., number of edges, which were both accepted by the algorithm and included in the prior model). The models generated using the database driven priors had significantly higher accepted priors compared to the randomly generated models (p < 0.05 Student's t-test for H0: μpsrandom = μpsdatabase-driven). Note that, we performed 500 parallel BP runs using identical, database driven prior models. We observed a low degree of variation in the number of accepted priors when the models are generated using the database driven priors. This is indicative of some solution degeneracy in the models. In predictive network modeling, we accounted for the solution degeneracy by re-computing the P(Wij) at the initial step of each BP-guided decimation calculation.
Figure 4—figure supplement 4
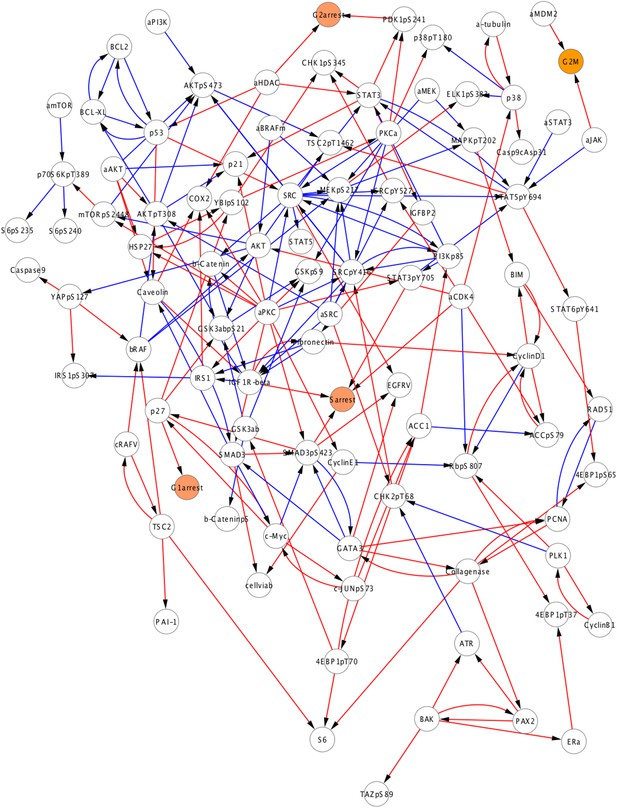
A subset of the prior information is represented in the average network model.
The average model, which was generated from the solutions inferred with the BP-guided decimation algorithm, contains 202 interactions in total and 89 of these interactions (blue edges) are also sampled in the qualitative prior model, which contains 154 interactions. 65 prior edges are not represented in the average model as the prior bias in network inference did not conform to the experimental data and not accepted frequently in the model ensemble. Note that a majority of the interactions in the prior set is sampled by only a fraction of the models; however, those interactions are not sufficiently strong and/or frequent that they are not captured in the average model (Figure 4—figure supplement 2).
Figure 4—figure supplement 5
Optimization of network inference cost function parameters.
We performed an error and connectivity analysis of BP-generated models with varying cost function parameters (sum-of-squares error [SSE]: β, model complexity: λ, prior information: κ). The network models are generated using the SkMel-133 proteomic/phenotypic response data and the BP-based inference method as in Figure 4—figure supplement 3. The SSE and model complexity (number of edges in the model) are calculated for each inferred model. We searched for the inference parameters that lead to low SSE and an intermediate model complexity (e.g., 1.5 < [(#edges)/(#nodes)] < 2.0). (A) The β and λ is incremented systematically while κ = λ. A low SSE with a desired connectivity level is reached for β = 2, λ = 5 and κ = 5. For different parameter sets, we obtained lower errors only for extremely connected networks inferred with high β values and so with a high weight on error in BP-optimization (e.g., β = 5, λ = 5, κ = 5, SSE = 3.8, #edges = 252). (B) The β and λ is incremented while κ is fixed (κ = 5) to determine the optimum solution with better SSE and connectivity level for (κ = 5). The parameter set, β = 2 and λ = 5 yielded the most desired SSE and connectivity values. (C) The κ is incremented for fixed β and λ (β = 2, λ = 5). The error is relatively insensitive to variations in κ as the final error is in the range of 5.6–6.1 for different κ values, although the connectivity increases with increasing prior strength in the cost function. This suggests that the error is mainly driven by the global β and λ terms at least around the tested β and λ values. Increasing κ, which is nonzero for only a small fraction (<2%) of possible interactions in the model, may enforce an increase in number of nonzero edges with an incremental effect on the error. κ = 5 yielded a desired connectivity value with a sufficiently low SSE. We used the parameter set (β = 2, λ = 5, κ = 5) in all BP-guided decimation calculations with the SkMel-133 data.
Figure 5 with 2 supplements
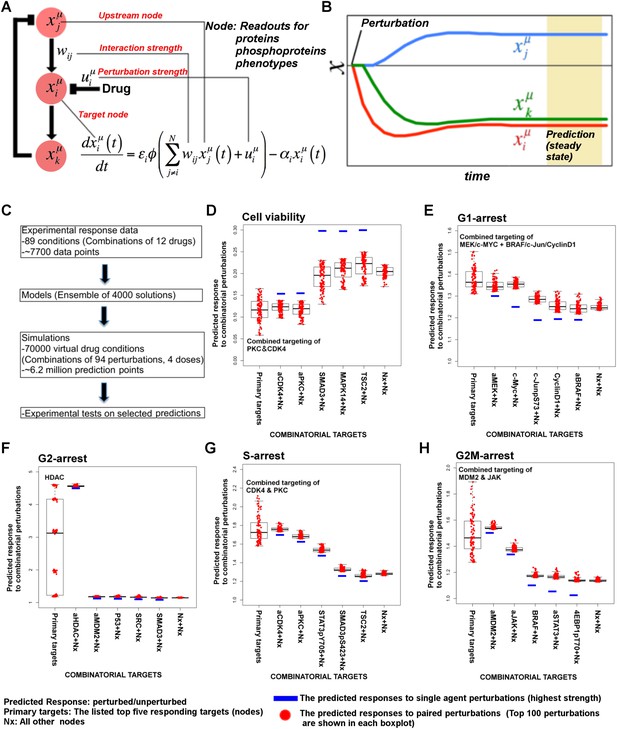
Simulations with in silico perturbations provide predictions on system response to novel perturbations.
(A) The schematic description of network simulations. The system response to paired perturbations is predicted by executing the ODE-based network models with in silico perturbations. In the ODE-based models, {Wij} represents the set of interaction strengths and is inferred with the BP-based modeling strategy. The in silico perturbations are applied as real-valued uim vectors. The time derivative and final concentration of any predicted node is a function of the model parameters, the perturbations, and the values of all the direct and indirect upstream nodes in the models. (B) The model equations are executed until all model variables (protein and phenotype responses) reach to steady state. The predicted response values are the averages of simulated values at steady state over 4000 distinct model solutions. (C) The simulations expand the response map by three orders of magnitude and generate testable hypotheses. (D–H) The predicted phenotypic response to combinatorial in silico perturbations. Each box contains the 100 highest phenotypic responses to paired perturbations. The first box includes the response predictions for combined perturbations on primary targets (e.g., aMEK, c-Myc for G1-arrest. Also see Table 1 for the definition of the term ‘primary target’). The second to sixth boxes include the predicted response for combined targeting of the primary targets with all other nodes (Nx). The last box represents the predicted response data for combination of all nodes except the primaries. For the complete predicted phenotypic response see Figure 5—figure supplements 1, 2.
Figure 5—figure supplement 1
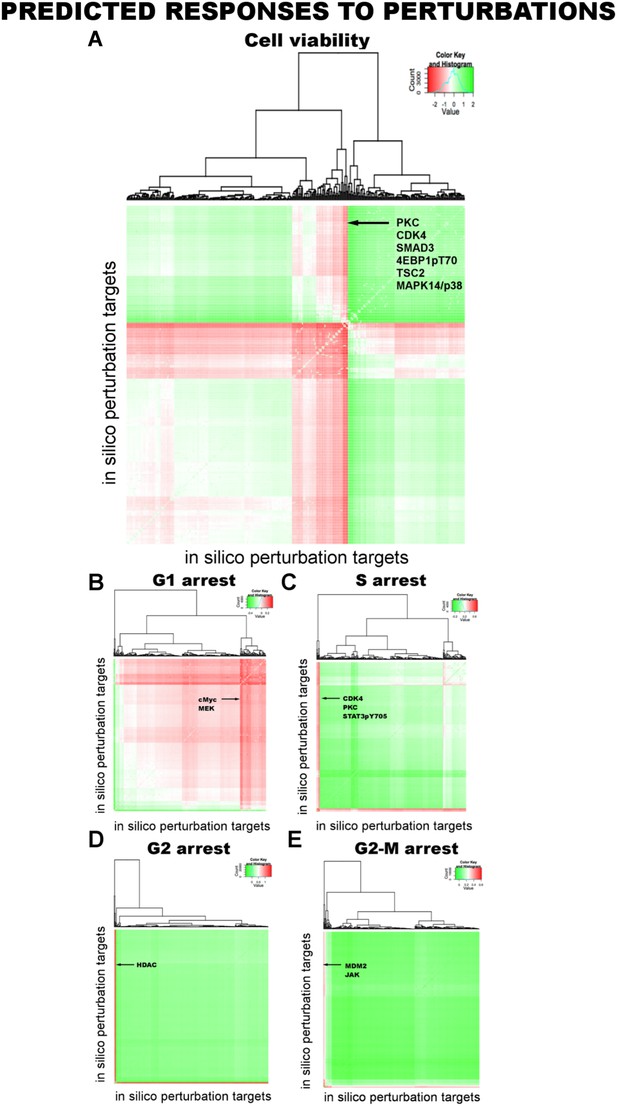
Prediction of phenotypic responses to in silico combinatorial perturbations.
We computationally predicted cell viability and cell cycle arrest (G1, S, G2, and G2M) in response to combinatorial perturbations on all proteomic nodes in the network models (see Table 1 and Figures 5, 6). In silico perturbations include paired combinations of 94 perturbations in four different perturbation strengths (equivalent to IC0-20-40-60-80 with respect to the basal level of a particular node) leading to more than 70,000 unique perturbation conditions. Each in silico perturbation is applied to 4000 inferred network models. This leads to a simulation of ∼28 million unique conditions for 99 different readouts and nearly a 2.8 billion total predicted readouts over all models, a scale inaccessible by most experimental screening methods. The heatmaps display the phenotypic response landscape to combinatorial perturbations. Each data point on the heatmaps is the response to a perturbation averaged over predictions from 4000 network models. (A) Cell viability response to combinatorial perturbations. The desired response from a perturbation is reduction in cell viability (red: decreased cell viability, green: increased cell viability). (B–E) Same as in A but for cell cycle progression phenotypes. For cell cycle phenotypes, the desired response is an increase in the cell cycle arrest (red: increased cell cycle arrest. green: decreased cell cycle arrest).
Figure 5—figure supplement 2
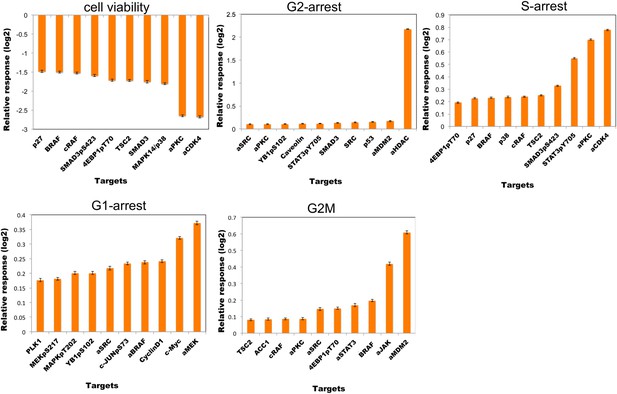
The top ten most effective single-agent in silico perturbations for each phenotype.
The listed proteomic entities for each phenotype are potential drug targets for slowing down the growth of melanoma cells. The error bars represent the ±SEM over the simulations of all model solutions.
Figure 6 with 4 supplements
The combined targeting of c-Myc with MEK and BRAF leads to synergistic response in melanoma cells.
(A) The isobolograms of predicted G1-response to combined targeting of c-Myc with MEK, BRAF, cyclin D1, and pJUNpS73. The leftward shift of isocurves implies synergistic interactions between the applied perturbations particularly for co-targeting of c-Myc with MEK or BRAF. u denotes strength of in silico perturbations. (B) RAFi inhibits MEK phosphorylation at S217 and MEKi inhibits ERK phosphorylation at T202 in a dose-dependent manner (first 2 gels). Western blot shows the level of c-Myc in response to JQ1, MEKi, RAFi, and their combinations (24 hr) (third gel). c-Myc expression is targeted with JQ1 combined with MEKi or RAFi. Direct target of JQ1, BRD4 protein is expressed in both control and 500 nM JQ1-treated cells (fourth gel) (See Figure 6—figure supplement 4 for uncropped western blot images). (C, D) The cell cycle progression phenotype in response to JQ1 and RAFi as measured using flow cytometry. 46% and 51% of cells are in G1-stage 24 hr after RAFi and JQ1 treatment, respectively. The combination has a synergistic effect on G1 cell cycle arrest (G1 = 84%). 39% of cells are in G1 when they are not treated with drugs. On panel D, error bars in right panel: ±SE in three biological replicates E. The drug dose–response curves of cell viability for MEKi + JQ1 (top) and RAFi + JQ1 (bottom). Cell viability is measured using the resazurin assay. Error bars: ±SEM in three biological replicates F. The synergistic interactions between JQ1 and RAFi/MEKi. 1 − Amax is the fraction of cells alive in response to highest drug dose normalized with respect to the nondrug treated condition (top panel). Combination index (CI) quantifies the synergistic interactions between drugs (bottom left). CI is calculated at a given level of inhibition and is a measure of the fractional shift between the combination doses (C1 and C2) and the single agent's inhibitory concentration (Cx,1, Cx,2).
Figure 6—figure supplement 1
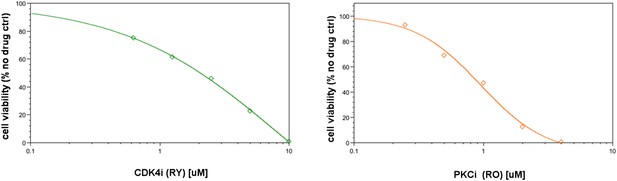
The cell viability response to CDK4i and PKCi.
The IC50 for CDK4i is ∼2 μM in SkMel-133 cells. The maximum response is reached at ∼10 μM. The IC50 for CDK4i is ∼1 μM and maximum response is reached at 4 μM in SkMel-133 cells. CDK4i (2μ) and PKCi (3.5–7 μM) were used in original input perturbation data. The models recapitulated the effect of high doses of PKC and CDK4 inhibitors required to decrease cell viability. However, no significant effect on viability is observed in the biologically more relevant nM range.
Figure 6—figure supplement 2
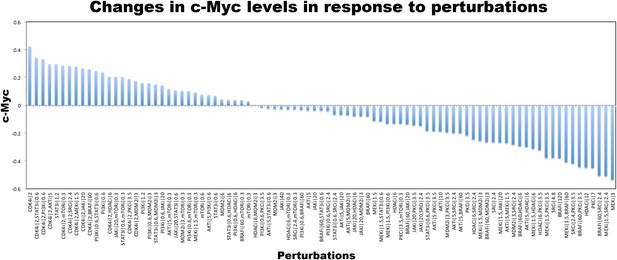
Changes in c-Myc level in response to perturbations in SkMel-133 cells as measured with RPPA experiments.
Each data point is log normalized with respect to the c-Myc level in unperturbed condition. c-Myc level is highest when cells are treated with CDK4i. Various drug combinations that include STAT3 and mTOR inhibitors follow CDK4i combinations. c-Myc level is lowest when cells are perturbed with MEK, BRAF, SRC, PKC, and HDAC inhibitors, respectively. Each data point is the average of RPPA readouts from three replicates.
Figure 6—figure supplement 3
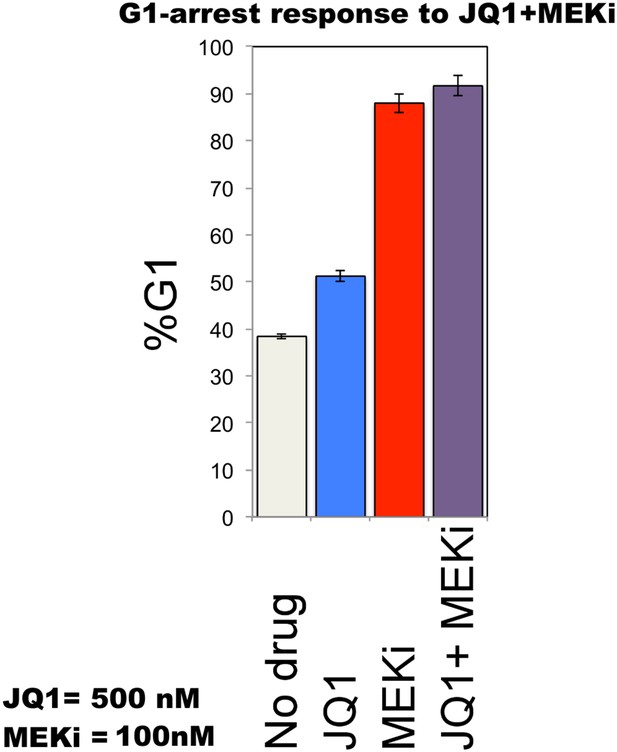
Cell cycle arrest response of melanoma cells to JQ1 and MEKi combination.
51% and 88% of cells are in G1-stage 24 hr after JQ1 and MEKi treatment, respectively. JQ1 + MEKi combination has an increased effect on G1 cell cycle arrest (G1 = 92%). 39% of cells are in G1 when they are not treated with drugs. Error bars in right panel: ±SE in three biological replicates.
Figure 6—figure supplement 4
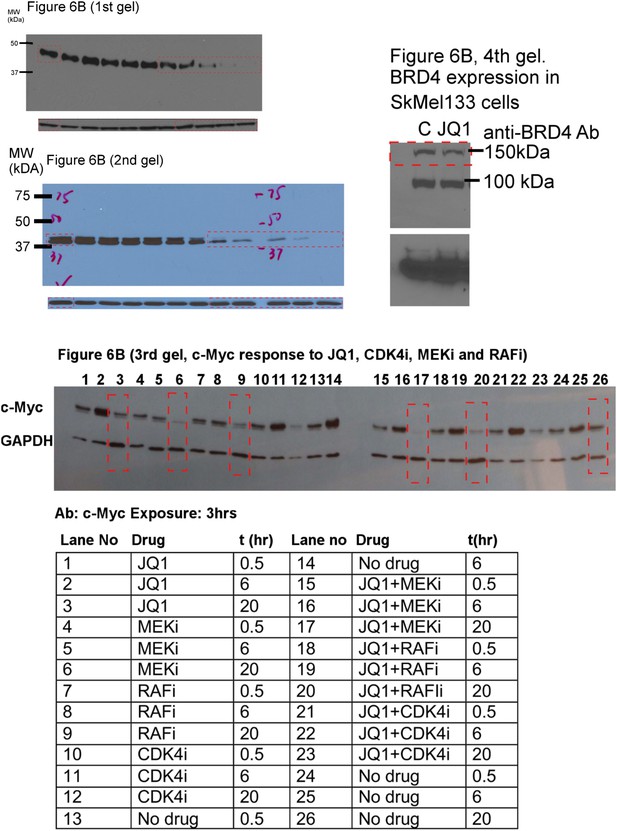
Uncropped versions of the gels presented in Figure 6B.
In the fourth gel, the observed band at ∼100 kDa is most likely the BRD4 B or C isoform.
Figure 7
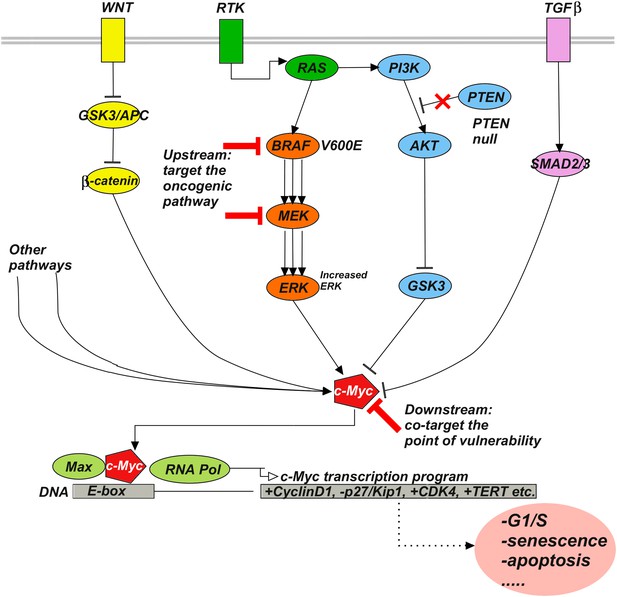
Upstream–downstream combination therapy.
Co-targeting a specific genomic upstream alteration (here, a BRAFV600E mutant) and a general downstream point of vulnerability (here, c-Myc) may be an effective strategy to overcome drug resistance, as it has the potential dual advantage of specificity and generality. The specificity of targeting an upstream oncogenic activator such as BRAFV600E reduces the likelihood of toxicity because normal cells depend much less or not at all on the activator. The generality of targeting a downstream signaling molecule such as c-Myc increases the likelihood of blocking diverse bypass mechanisms. Signaling pathways such as Wnt, RTK, TGFβ, and various others influence c-Myc stability, expression, and activity. For example, ERK phosphorylates c-Myc at S62 to stabilize the molecule, while phosphorylation at T58 by GSK3 leads to ubiquitylation and degradation. β-catenin and SMAD3 act as transcriptional activator and repressor of c-Myc, respectively. RAF-inhibitor resistance can, for example, be mediated by the activities of the Wnt (Anastas et al., 2014), TGFβ (Sun et al., 2014), or RTK (Villanueva et al., 2010; Xing et al., 2012) pathways.
Tables
Table 1
Phenotypic nodes and predicted responses from simulations with in silico perturbations
| Phenotype | Immediate upstream nodes (<wij> in average model) | Predicted primary target* | Predicted combination partners |
|---|---|---|---|
| Cell viability | SMAD3 (0.49) | aPKC | SMAD3, 4EBP1pT70, TSC2, MAPK14/p38 |
| cyclin E1 (−0.28) | aCDK4 | ||
| G1-arrest | p27/KIP1 (0.83) | c-Myc | Cell cycle (cyclin B1, RBpS807, cyclin D1, PLK1), MAPK pathway (MAPKpT202, MEKpS217, BRAF, aBRAF), AKT, AKTpT308, RAD51, p38/MAPK14, aSRC, YBIpS102, cJUNpS73, SMAD3 |
| PDK1pS241 (0.20) | aMEK | ||
| G2-arrest | aHDAC (−0.77) | aHDAC | Generic response from all nodes |
| S-arrest | STAT3pY705 (−0.66) | aCDK4 | aPKC, SMAD3pS423, STAT3pS705, IGFBP2, cyclin B1, IGF1Rβ, Fibronectin |
| IGF1Rβ (−0.20) | |||
| SMAD3pS423 (−0.23) | aPKC | STAT3pS705 | |
| aCDK4 (−0.49) | |||
| G2M | aJAK (−0.24) | aMDM2 | aJAK, aSTAT3, BRAF, 4EBPpT70 |
| aMDM2 (−0.38) |
-
*
A proteomic node is a primary target when substantial phenotypic change is predicted in response to perturbation of the node alone. The phenotypic response is further increased when the primary targets are perturbed in combination with a set of other nodes (i.e., the combination partners). Also See Figure 5D–H, Supplementary file 1D and Figure 5—figure supplements 1, 2.
Table 2
Drug resistance is overcome as the IC50 (cell viability) approaches the IC50 (target phosphorylation)
| JQ1 | MEKi | RAFi | |
|---|---|---|---|
| IC50 (target phosphorylation) | – | 3 nM* | 65 nM* |
| IC50 (cell viability) single agent | 200 nM | 15 nM | >1 μM |
| IC50 (cell viability) combined with JQ1 | – | 5 nM† | 120 nM† |
-
*
MEKi targets pERK and RAFi targets pMEK. Phopho-IC50s are quantified from gels (Figure 6B).
-
†
IC50s for viability and phosphorylation are in same order.
Additional files
-
Supplementary file 1
(A) Drugs used in perturbation experiments. (B) Proteins that respond to at least one perturbation and exist in models. (C) Perturbation conditions. (D) Predicted G1-arrest response to combined targeting of c-Myc and other nodes (Perturbations on c-Myc + X). (E) Statistical validation of perturbation models. (F) Predicted co-targeting strategies in SkMel133 cell line.
- https://doi.org/10.7554/eLife.04640.029
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Perturbation biology nominates upstream–downstream drug combinations in RAF inhibitor resistant melanoma cells
eLife 4:e04640.
https://doi.org/10.7554/eLife.04640
