Additive effects on the energy barrier for synaptic vesicle fusion cause supralinear effects on the vesicle fusion rate
Figures
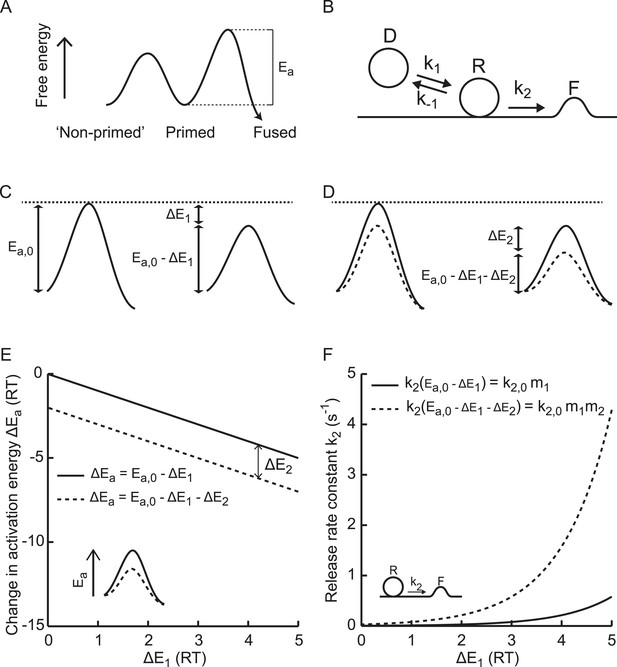
Supralinear modulation of synaptic efficacy through additive effects on the activation energy for fusion.
(A) Schematic of the energy landscape for synaptic vesicle priming and fusion, with Ea the activation energy for vesicle fusion, and (B) the corresponding vesicle-state model. (C) Reduction of the fusion activation energy at rest Ea,0 by an amount ΔE1, or (D) by a combined effect of ΔE1 and ΔE2. (E) Additive effect of ΔE2 causes a constant shift of the effective activation energy for fusion ΔEa for different values of ΔE1, but a (F) multiplicative effect on the release rate constant k2.
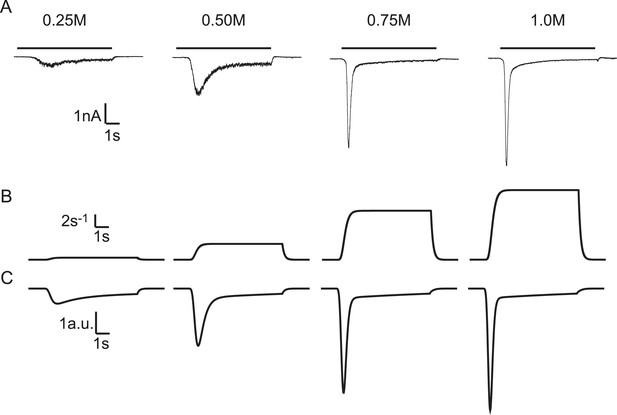
Modelling HS-induced EPSCs.
(A) Concentration dependence of HS-induced release kinetics. (B) Model simulations of time courses of k2, for different values of k2,max and (C) corresponding synaptic responses (−k2R).
-
Figure 2—source data 1
Parameter values for Figure 2—figure supplements 1 and, 3.
- https://doi.org/10.7554/eLife.05531.005
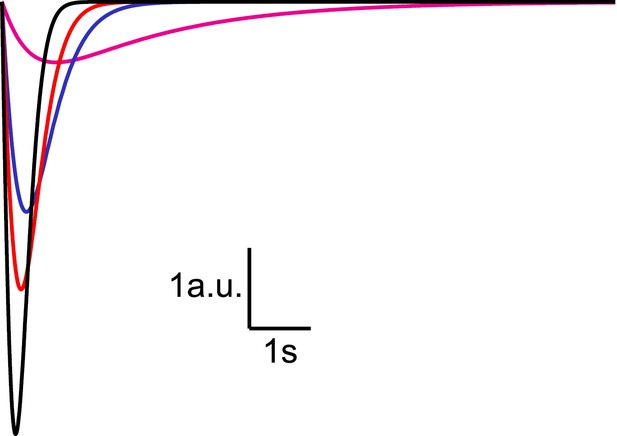
Analytical solution for hypertonic sucrose-induced release from a RRP without replenishment.
Current responses obtained from Equation (14) after convolution with a typical mEPSC. The magenta line corresponds to k2,max = 0.5 s−1, blue to k2,max = 3 s−1, red to k2,max = 5 s−1, and black to k2,max = 10 s−1.
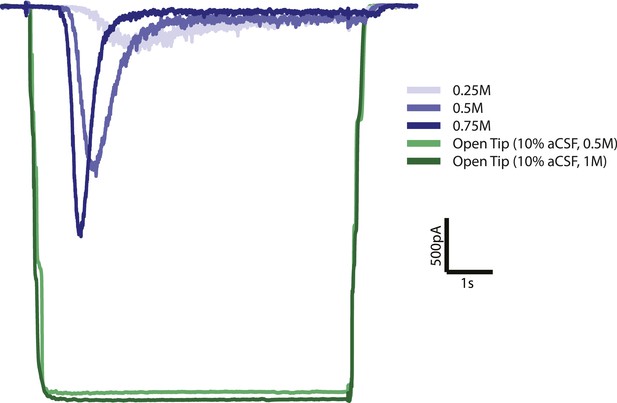
Open tip experiments show rapid solution exchange.
Solution exchange was measured by the change in holding current when switching from normal (0.3M) extracellular solution to 10 times diluted (0.03M) extracellular solution with 0.5 or 1M sucrose. Green curves are the average responses for 6 recordings, corrected for baseline and inverted for displaying purposes. Blue curves represent postsynaptic current responses to different sucrose concentrations which show a delayed response with respect to the sucrose stimulus.
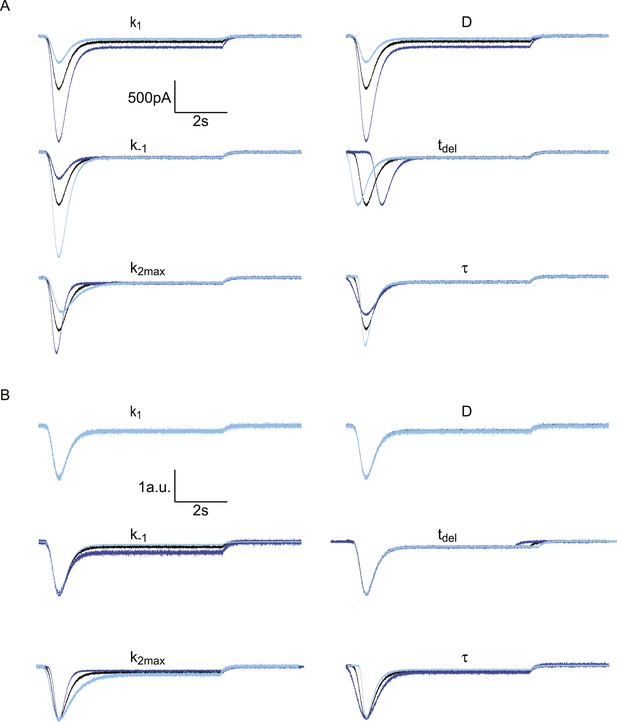
Effect of different model parameters on simulated HS-induced EPSCs.
The default parameter set, represented by the black traces, is . In each subpanel, one of these parameters is either multiplied by 2 (dark blue) or divided by 2 (light blue). The Gaussian white noise added to these curves was generated using the MATLAB ‘randn()’ function, with µ = 0 pA and σ = 10 pA. (A) Absolute traces. (B) Traces scaled and aligned to peak.

Probing the energy barrier for synaptic vesicle fusion.
(A1) HS induced EPSCs (black) with model fits (red) superimposed. (A2) Spontaneous vesicle release at 0M sucrose. (B) RRP size obtained from model fits using Equation (9). (C) Fitted maximal release rate constants k2,max at different sucrose concentrations. (D) Changes in activation energy (at 293 K) obtained from values for k2,max in C using Equation (5). Data for 0.25M and higher were fitted with a monoexponential function, which was transformed into the dose–response curve in C using the equations given in Figure 3—source data 1.
-
Figure 3—source data 1
Parameter values for Figure 3B–D, bootstrap analysis Figure 3, Figure 3—figure supplement 1A–C, bootstrap analysis Figure 3—figure supplement 1, Figure 3—figure supplement 3B–E, and Figure 3—figure supplement 4B–E.
- https://doi.org/10.7554/eLife.05531.010
-
Figure 3—source data 2
Parameter values for Figure 3—figure supplement 5A and ,C.
- https://doi.org/10.7554/eLife.05531.011
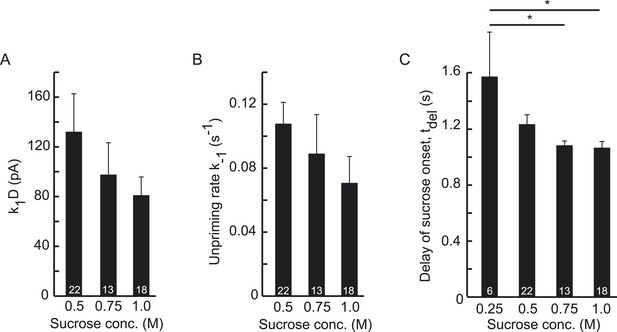
Higher concentrations of hypertonic do not significantly affect upstream parameters but reduce the delay of sucrose action onset with respect to time of switching of the application barrel.
(A) Priming rate k1D, (B) Unpriming rate constant k−1, and (C) Delay of sucrose onset, tdel.
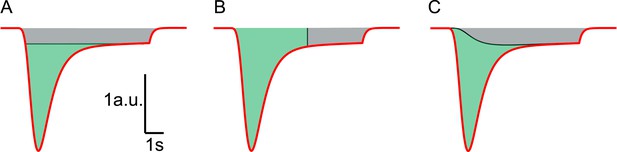
Different methods to estimate RRP size from HS responses.
Red line represents a typical current response in a.u. induced by hypertonic stimulation. (A) HS induced current response is corrected for vesicle replenishment by taking the steady state current at the end of the response as baseline and subtracting this from the total current. Integration of the corrected current response yields the RRP size in nC, or in vesicles, after dividing total charge by the quantal content of a single mEPSC (green area) (Basu et al., 2007; Arancillo et al., 2013). This gives an underestimation of the RRP since vesicle replenishment does not start at the maximal rate at the onset of the response but grows gradually during the stimulation. (B) RRP size is estimated from integration of the total charge transfer from the beginning of the response to an arbitrary timepoint after the peak (green area), neglecting any contribution from vesicle replenishment (grey area) (Reim et al., 2001; Rosenmund et al., 2002; Toonen et al., 2006; Ikeda and Bekkers, 2009). This usually leads to an overestimation. (C) In this paper, the definition of the steady state RRP in Equation (9) is used to infer the RRP size from the fitted model parameters. Effectively, in comparison to methods shown in A and B, we correct for vesicle replenishment by subtracting the calculated vesicle replenishment using Equation (20) (black line) from the total current. Integration of the corrected HS induced current response yields an accurate estimation of the RRP (green area).

Effect of the non-selective glutamate receptor antagonist kynurenic acid (KYN) on release kinetics.
(A) Current traces induced by 0.5 or 0.75M sucrose in the presence or absence of 0.2 mM KYN (measured in the same neuron). Shown are raw and scaled traces. Insets show zoom of 0.75M peak. (B–D) KYN induced changes in (B) release rate constant k2,max (C) RRP size, (D) priming rate k1Dk1D, (E) unpriming rate constant k−1. Parameters are obtained from unscaled raw data and normalized to the condition without KYN. Since KYN reduced the measured current, RRP size and priming rates are reduced. The maximal release rate is unaffected in 0.5M sucrose, but increased by KYN in 0.75M sucrose. This suggests that post-synaptic receptor saturation might play a role in sucrose concentrations of 0.75M or higher.
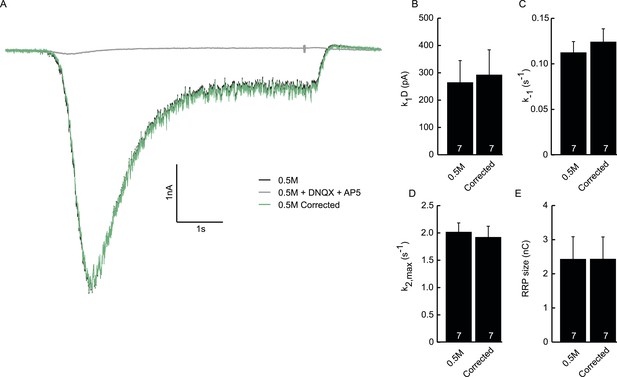
Subtraction of non-receptor current does not affect fitted model parameters.
(A) Example trace of postsynaptic response evoked by 0.5M sucrose (black). Green trace is corrected for the non-receptor current induced by 0.5M in the presence of AMPA and NMDA blockers DNQX (10 µM) and APV (50 µM) (grey). (B) Priming rate k1D. (C) Unpriming rate constant k−1. (D) Release rate constant k2,max. (E) RRP size.

Fitting HS-induced EPSCs.
(A) The default parameter set is as in Figure 2—figure supplement 3. Each panel shows the first 4 s of the simulated trace per parameter setting in black. Traces are overlaid with results of 10 independent fits starting at different initial conditions, shown in red (best fit), green (accepted fit upon visual inspection) and grey (rejected fit upon visual inspection). With the exception of the results for 2k−1, the same scale holds for all curves. (B) Key features encircled in red to judge quality of the fit by visual inspection: (1) Late onset of fit, (2) wrong peak amplitude and/or time-to-peak, (3) too slow decay towards steady state phase, (4) Steady-state phase (refill) is fitted incorrectly. (C) Fit method robustly discriminates between different model parameters. Graphs display fitted model parameters, obtained from fits approved after visual inspection in (A) (red and green curves), as a function of the adapted model parameter. Strong linear correlation is found for the adapted model parameter, whereas the other parameters are invariant.
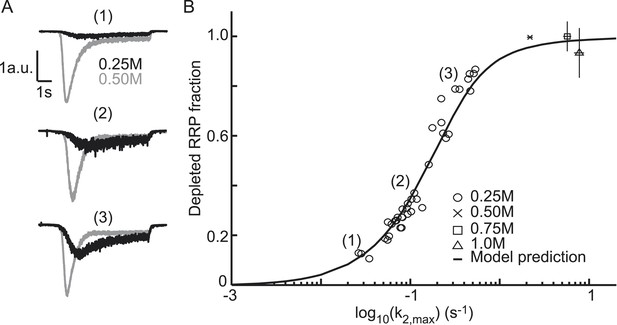
Relation between depleted RRP fraction and release kinetics.
(A) Examples of submaximal responses in different cells. 0.25M responses (black), scaled to 0.5M responses (grey) in the same cell, display faster kinetics when a larger fraction of the RRP is depleted. (B) Fitted data overlayed on the predicted curve. Data points corresponding to the examples in A are indicated. Data points for 0.50M, 0.75M, and 1.0M are shown as mean ± SEM. Note that whereas the model predicts a 94% depletion of the RRP with 0.5M the y-axis value at 0.5M is one per definition since the RRP size at this concentration was used as a reference to calculate the depleted RRP fraction.
-
Figure 4—source data 1
Parameter values for Figure 4B and Figure 4—figure supplement 1.
- https://doi.org/10.7554/eLife.05531.018
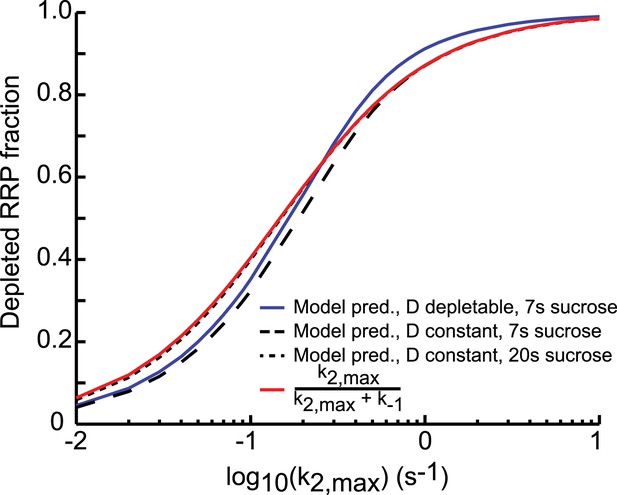
Comparison of analytical approximation and model predictions of the relation between release kinetics and RRP depletion.
For small k2,max, the duration of the sucrose pulse dictates the depleted RRP fraction: 7 s stimuli deplete a smaller fraction than stimuli of 20 s and longer. For large k2,max, the blue curve (D depletable) exceeds the others, because the steady-state RRP at the end of the stimulus is smaller when D is depletable. This is due to Equation (24): Rf = k1Df/(k−1 + k2,max). A smaller upstream pool at the end of the stimulus (Df) thus yields a smaller Rf and hence a larger depleted RRP fraction (Ri − Rf)/Ri.
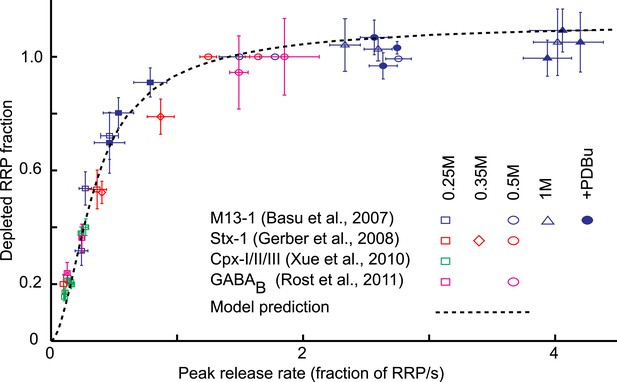
Model predicts relation between peak release rate, defined as the release rate at the peak of a HS-induced response, and depleted RRP fraction for different combinations of HS stimulations and genetic or biochemical manipulations of the activation energy for fusion.
Data are taken from (Basu et al., 2007; Gerber et al., 2008; Xue et al., 2010; Rost et al., 2011) Model prediction is obtained from peak release rates and depleted RRP fractions extracted from model simulations where parameter k2,max is varied keeping other model parameters constant. Note that beyond 0.5M the predicted curve and some data points overshoot the value of one because 0.5M was used as a reference to calculate the depleted RRP fraction at the other concentrations, assuming complete depletion at 0.5M, whereas the model predicts only 94% depletion at this point.
-
Figure 5—source data 1
Parameter values for Figure 5.
- https://doi.org/10.7554/eLife.05531.021
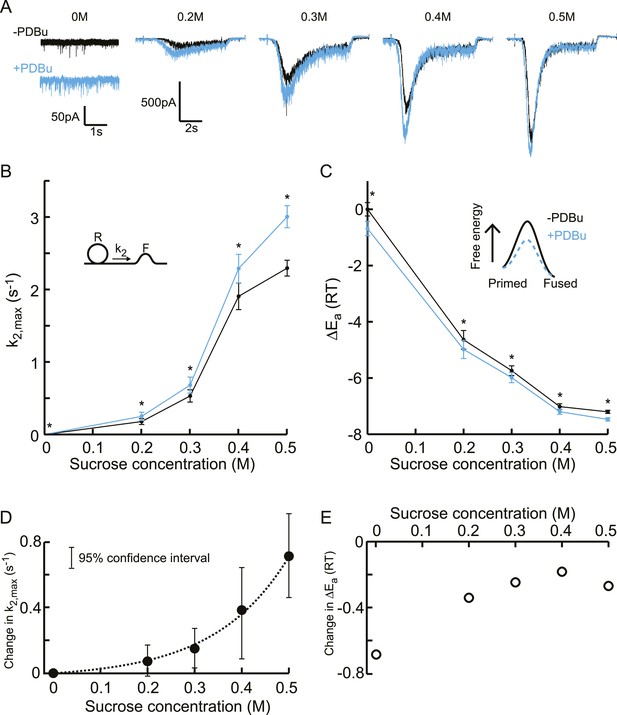
Additive effect on the activation energy for fusion induced by PDBu causes supralinear effect on release kinetics.
(A) Current traces, (B) release rate constants k2,max, and (C) activation energies for fusion at different sucrose concentrations in the absence and presence of PDBu. PDBu-induced changes in k2,max and ΔEa, obtained by subtraction of the data curves in B and C before and after PDBu application, show (D) an exponential increase in k2,max for increasing sucrose concentrations whereas (E) the changes in the energy domain are in the same order of magnitude (reduction at 0M is probably an overestimation due to Ca2+ depenence of the spontaneous release, [see text]). Mean values of k2,max displayed are all within the 95% confidence interval as determined by Bootstrap analysis.
-
Figure 6—source data 1
Parameter values for Figure 6B–E, bootstrap analysis Figure 6, Figure 6—figure supplement 3A–D, and Figure 6—figure supplement 3.
- https://doi.org/10.7554/eLife.05531.023
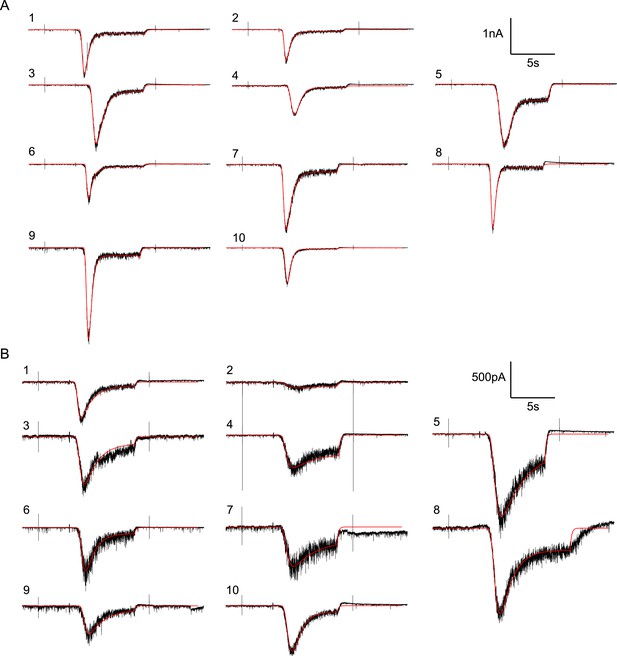
Random examples of individual HS-evoked EPSCs (black) in the absence of PDBu, overlaid with their best fit (red).
(A) Responses to 0.5M. (B) Responses to 0.3M.

Random examples of individual HS-evoked EPSCs (blue) in the presence of PDBu, overlaid with their best fit (red).
(A) Responses to 0.5M. (B) Responses to 0.3M.
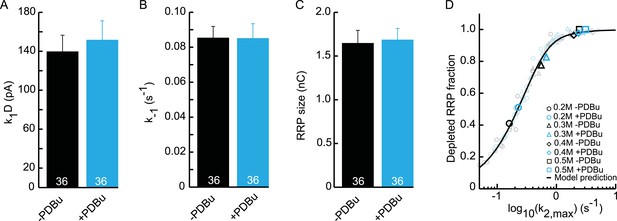
Upstream parameters and RRP size are not affected by PDBu application.
(A) Priming rate k1D. (B) Unpriming rate constant k−1. (C) RRP size. (D) Relation between k2,max and depleted RRP is maintained in the presence of PDBu, but synaptic responses to submaximal HS-stimulation display faster kinetics and more RRP depletion.
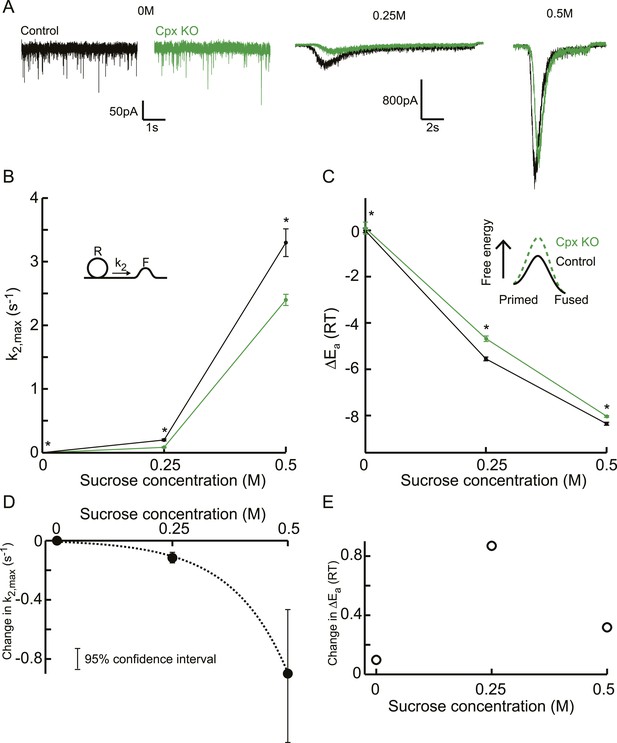
Additive effect on the activation energy for fusion induced by Cpx deletion causes supralinear effect on release kinetics.
(A) Current traces, (B) release rate constants k2,max, and (C) fusion energy barrier heights at different sucrose concentrations for control and CpxKO cells. Cpx deletion-induced changes in k2,max and ΔEa, obtained by subtraction of the data curves for control and CpxKO in B and C, show (D) an exponential increase in k2,max for increasing sucrose concentrations whereas (E) the changes in the energy domain are in the same order of magnitude. Mean values of k2,max displayed are all within the 95% confidence interval as determined by Bootstrap analysis. Cpx data were published before in (Xue et al., 2010) and reanalysed here.
-
Figure 7—source data 1
Parameter values for, bootstrap analysis Figure 7B–E, bootstrap analysis Figure 7, Figure 7—figure supplement 1A–D, and bootstrap analysis Figure 7—figure supplement 1.
- https://doi.org/10.7554/eLife.05531.028
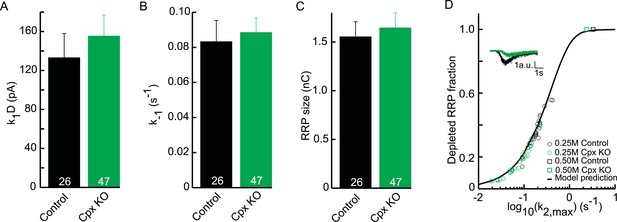
Upstream parameters and RRP size are not affected in Cpx KO.
(A) Priming rate k1D. (B) Unpriming rate constant k−1. (C) RRP size. (D) Relation between k2,max and depleted RRP is maintained in Cpx KO synapses, but synaptic responses to submaximal HS-stimulation display slower kinetics and less RRP depletion.
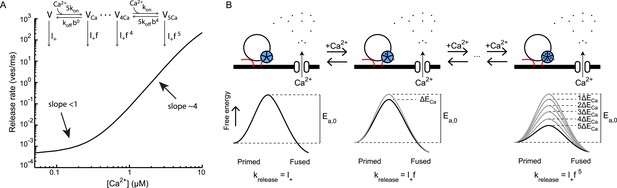
Supralinear Ca2+ dependency of release can be explained by additive modulation of the activation energy for fusion by the Ca2+ sensor.
(A) Non-linear relation between Ca2+ and release rate in the Calyx of Held as predicted by the allosteric model of Lou et al. (2005). Allosteric model with 6 different vesicle states is depicted in inset. (B). Reinterpretation of this allosteric model in terms of additive effects on the activation energy of the binding of Ca2+ to the Ca2+ sensor: each Ca2+ ion that binds reduces the activation energy Ea, 0 by an amount ΔECa. From Equation (4) it follows that for each vesicle state the release rate constant krelease is given by Equation (6), with the spontaneous release rate constant and a multiplication factor. This is mathematically equivalent to the release rate constants depicted for the different vesicle states in the allosteric model in A and thus yields the same prediction of the non-linear relation between Ca2+ and release rate.
Additional files
-
Source code 1
Custom software to analyze HS-induced postsynaptic currents written in MATLAB (only compatible with MATLAB R2013 or older). Instructions for how to use the program are in the readme file. Use on a Mac or Linux system requires specification of the location of the poi_library when asked for by the program.
- https://doi.org/10.7554/eLife.05531.031





