MorphoGraphX: A platform for quantifying morphogenesis in 4D
Figures
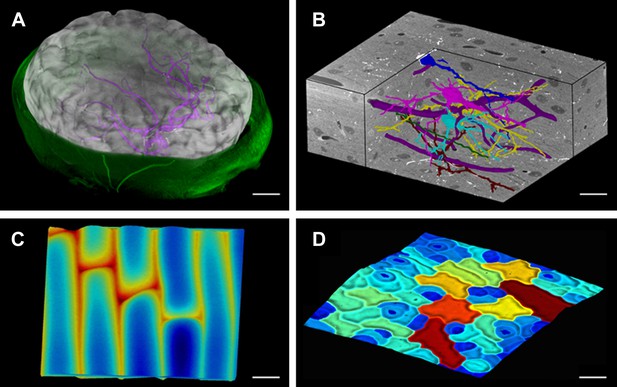
MorphoGraphX renderings of 3D image data and surfaces.
(A) Extraction of a brain surface (gray, semi-transparent surface colored by signal intensity) from a Magnetic Resonance Angiography scan of an adult patient (IXI dataset, http://www.brain-development.org/). Surrounding skull and skin (green) have been digitally removed prior to segmentation. Voxels from the brain blood vessels are colored in purple. (B) Serial block-face scanning electron microscopy (SEM) images of mouse neocortex (Whole Brain Catalog, http://ccdb.ucsd.edu/index.shtm, microscopy product ID: 8244). Cutaway view (gray) shows segmented blood vessels (dark purple) and five pyramidal neurons colored according to cell label number. (C) Topographic scan of onion epidermal cells using Cellular Force Microscopy (Routier-Kierzkowska et al., 2012), colored by height. (D) 3D reconstruction of Arabidopsis thaliana leaf from stereoscopic SEM images (Routier-Kierzkowska and Kwiatkowska, 2008), colored by cell size. Scale bars: (A) 2 cm, (B and C) 20 μm, (D) 30 μm.
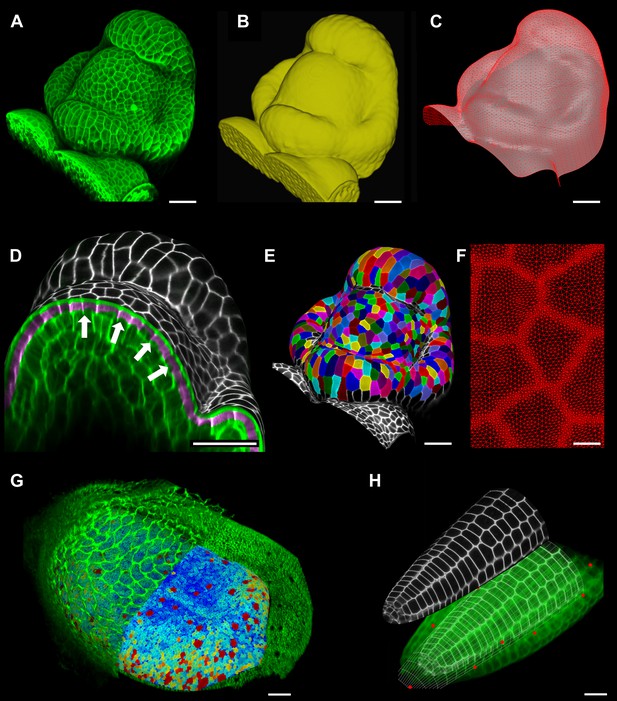
Feature extraction and 3D editing of confocal image stacks.
A sample workflow from raw data to segmented cells is presented for an A. thaliana flower (A–F). (A and B) After removing noise with 3D filters, the stack (green) is converted into a mask using edge detection (yellow). (C) A coarse representation of the surface is extracted with marching cubes, then smoothed and subdivided. (D) After subdivision, a thin band of signal representing the epidermal layer (purple) is projected onto the mesh, giving a clear outline of the cells. Note that the projection is perpendicular to the curved surface and its depth is user-defined (in this case, from 2 to 5 μm). (E) The surface is then segmented with the watershed algorithm, which we adapted to work on unstructured triangular meshes. (F) Closeup of adaptive subdivision, with finer resolution near cell boundaries. A similar process flow was used to segment shoot apical meristem in tomato (Kierzkowski et al., 2012; Nakayama et al., 2012) and A. thaliana (Kierzkowski et al., 2013), as well as Cardamine hirsuta leaves (Vlad et al., 2014). (G) 3D editing tools can be used to expose internal cell layers prior to surface extraction. Cell shapes extracted from the curved pouch of a Drosophila melanogaster wing disc, after removing signal from the overlying peripodial membrane (Aegerter-Wilmsen et al., 2012). Alternatively, the stack can be cleaned by removing voxel data above an extracted mesh or conserving only the signal at a defined distance from the mesh, as shown in purple in (D) and Figure 2—figure supplement 2. (H) MorphoGraphX also provides tools to project signal on arbitrary curved surfaces defined interactively by moving control points (red). A Bezier surface is highly bent to cut through the cortical cells of a mature A. thaliana embryo. Scale bars: 2 μm in (F), 20 μm in all other panels.
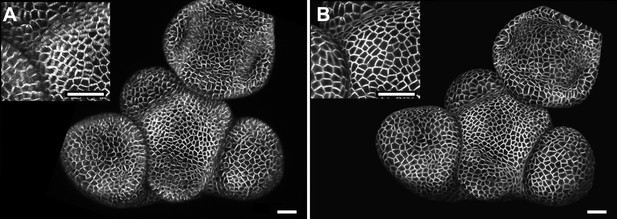
Maximal projection vs projection of signal on curved surface.
(A) Flat maximal projection of the membrane protein PIN1::GFP in an Arabidopsis inflorescence meristem using ImageJ. (B) The same confocal stack analysed in MorphoGraphX was used to extract a surface mesh first, then project the signal normal to the surface at a depth from 1 to 5 μm. In the case of curved organs like the shoot apical meristem of Arabidopsis, maximal projection (close up inset A) results in distortions that make it difficult to interpret the image (i.e., determine PIN1 polarization) or track changes in cell shape. The projection method used in MorphoGraphX (inset B), on the other hand, is less prone to artefacts. Scale bars 20 μm.

Mesh-volume interaction.
The original volumetric data (A) can be trimmed using a surface, either to clean up the data for further segmentation or to display the part of the data which was projected. Here we kept only the volumetric data located between 2 to 5 μm from the curved surface (B), showing what part of the signal was projected onto the surface to obtain the cell outline in main Figure 2D. Scale bar 20 μm.
Quantification of signal projected on the mesh surface.
(A) Microtubule orientation (red line) determined in epidermal cells of C. hirsuta fruits. Signal for TUA6-GFP (green) at a maximal depth of 1.5 μm was projected on the curved surface and processed with a modified version of a 2D image analysis algorithm (Boudaoud et al., 2014) to compute fiber orientation. Line length indicates strength of orientation. (B) Quantification of vestigial (left) and wingless (right) transcription in the wing disc of D. melanogaster at 0–20 μm depth. Data from (Aegerter-Wilmsen et al., 2012). (C and D) Quantification of PIN1::GFP signal in Arabidopsis shoot apical meristem at different depths. A projection between 0 and 6 μm away from the surface corresponds to the epidermal (L1) layer (C), while a depth of 6–12 μm reflects the sub-epidermal (L2) layer. (E) Sub-cellular localization of PINFORMED1 (PIN1) in the L1 is assessed by quantification of the projected signal for each cell wall, as in (Nakayama et al., 2012). The projected PIN1 signal can be compared with other markers of organ initiation, such as the curvature. While projected PIN1 signal from the L1 (C and E) shows a clear accumulation of signal at the incipient primordium (star), there is no sign of up-regulation in the deeper layer (D) nor visible bulge yet (see Figure 3—figure supplement 1). (C–E) Data from (Kierzkowski et al., 2013). Scale bars: 20 μm.
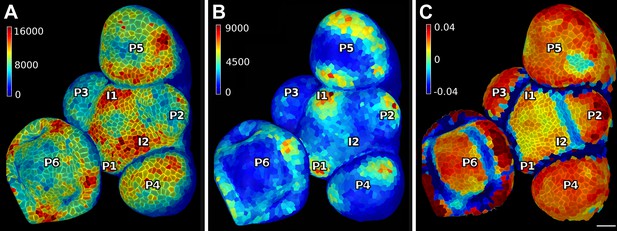
PIN1 expression levels in L1 and L2 vs curvature in Arabidopsis inflorescence meristem.
(A and B) show PIN1::GFP signal quantification respectively in the epidermal (L1) and sub-epidermal (L2) layers, as in main Figure 3. (C) Tissue curvature for a neighborhood of 10 μm, with positively curved areas in red and negatively curved on blue. Phyllotactic order (P6, P5, ..., I1, I2) is indicated, based on PIN1 expression and curvature. I2 marks the youngest incipient primordium, with no apparent bulging nor peak of PIN1 expression in the L2 yet, but PIN1 up-regulation already visible in L1 layer. Scale bar 20 μm.

Quantification of PIN1-GFP signal localized to close to the membrane vs internal signal.
(A) Projection of PIN1-GFP signal on the curved mesh surface extracted from a young flower bud. (B) Quantification of the average internal signal in each cell, in arbitrary units. (C) Quantification of membrane signal, in arbitrary units. (D) Ratio of internal vs total signal per cell. All signals (total, internal and membrane) are here averaged over the total area of the triangles used for the computation. Membrane and internal signal are distinguished based on the distance to the cell border. The signal from vertices closer than 0.7 µm to the cell outline is considered as membrane signal, while vertices farther than this threshold are considered internal. Note that the resolution of classical confocal images (A) does not allow the separation of plasma membrane signal from two adjacent cells in this case where the cell walls are very thin. It is only possible to distinguish PIN1 localization, not polarity. The use of other imaging techniques, such as hyper-resolution microscopy, could potentially allow a precise quantification of PIN1 polarization at the individual cell level in MorphoGraphX. In organs with larger cells, a more sophisticated analysis of the signal near the walls, such as that used in the CellSeT software (Pound et al., 2012), could be implemented for curved surfaces. Scale bar: 10 µm.
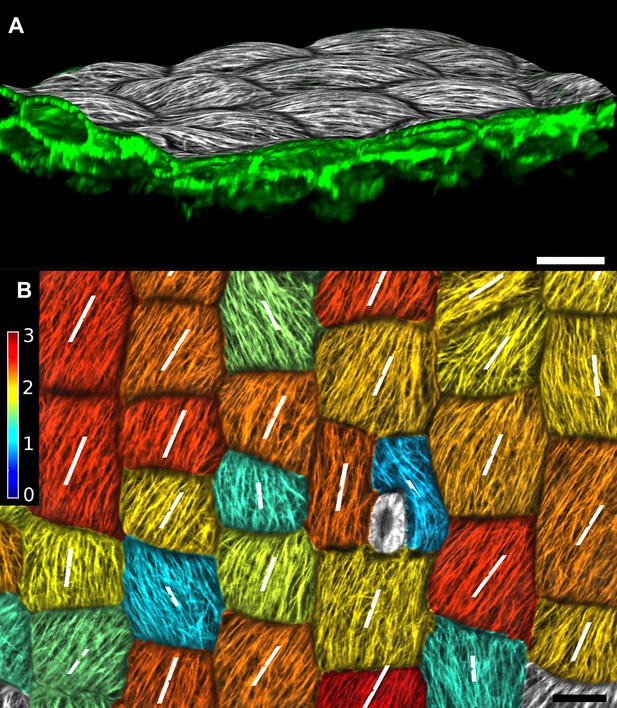
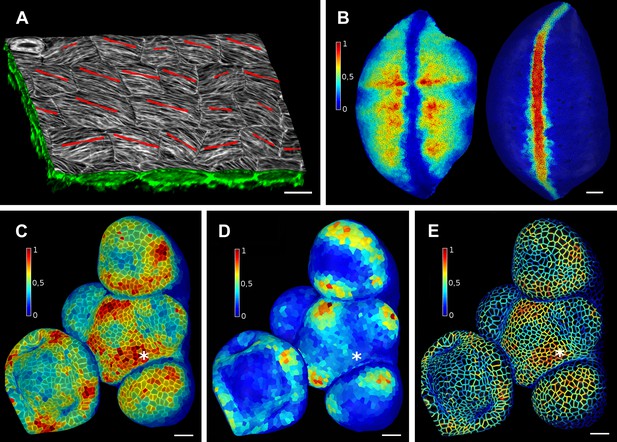
Quantification of microtubule orientation.
We adapted the FibrilTool ImageJ plugin (Boudaoud et al., 2014) to extract fibril orientations in MorphoGraphX. While the original algorithm was written for 2D unsegmented images, our implementation works on our curved surface images. This presents an advantage for highly curved organs or cells, as is the case with the Cardamine fruit epidermis (A). In addition, the use with segmented images allows the border exclusion zone to be assigned automatically, substantially reducing the clicking required and greatly increases throughput. Fiber orientation is determined by finding the principal component of color gradient within each cell. The main orientation of fibers (B, white segments) is perpendicular to the direction of maximal gradient. The degree of fiber orientation (B, colormap), or anisotropy, is given by the formula: (gradientMax/gradientMin -1). The adapted algorithm in MorphoGraphX allows us to directly combine various types of quantifications, for example, growth direction, PIN localization and MT orientation, on the same dataset. Scale bars: 20 µm.

Growth in the tomato shoot apex over 22 hr.
(A) Expression of the auxin activity reporter pDR5::VENUS visualized underneath the semi-transparent mesh. (B) Average curvature (μm−1) for a neighborhood of 20 μm, with positive values in red, and negative values in blue. (C) Shoot apex surface colored by cell proliferation rate as in (Vlad et al., 2014). New cell walls are indicated in dark red. (D) Top and side views of the heat map of areal expansion over the first 11 hr interval. Principal directions of growth (PDGs) are indicated for cells displaying an anisotropy above 15%, with expansion in white and shrinkage in red. Note the rapid anisotropic expansion of the developing primordium P1 and of the peripheral zone close to the incipient primordium I1, while cells in the boundary between P1 and the meristem contract in one direction (red lines). Arrows indicate the correspondence between top and side views. Raw confocal data from (Kierzkowski et al., 2012). Scale bars 50 μm.

Simplification of mesh.
(A) After several rounds of signal projection, segmentation with watershed and mesh sub-division, the final mesh has a finer resolution at the cell borders than in the rest of the cell. (B) A simplified version of the mesh can be created, to conserve only some of the vertices from the cell outline (in red) and the cell centers (in orange). This simplified mesh can be used to compute cell shape and tissue curvature, or to study the neighborhood information within a tissue. (C) The mesh can be even more simplified to keep only the cell junctions (green dots), cell boundaries represented by edges (red) and centers (not shown). This representation is used in the computation of PDGs. Simplified meshes are also useful to export for use as starting geometry for simulation models. Scale bar 5 μm.

Computation of PDGs in case of anisotropic deformation.
In (A and B) the cell outline is simplified to keep only the junctions (see Supplementary Figure 4C). Mother cells (A) on the first time point and their daughters (B) on the second time point are identified using the lineage tracking tool. The same junctions (green dots) are identified on both time points using the cell neighborhood information. Notice that new junctions generated by cell division on the second time point have no match. Pairs of matched vertices between the two time points are then used to computed the PDGs for each cell. The result can be visualized either on the first (C) or second (D) time points of the simplified meshes. PDGs can also be saved and re-loaded for display on the original, fine meshes (E and F). Different colors can be used to visualize expansion (in white) and contraction (in red) on the axis (G and H). The results of the PDG computation can also be visualized as heat maps, by coloring each cell according to the magnitude of deformation in the maximal (G) or minimal direction (H), or by other quantities (i.e., anisotropy, etc). Blue cells in (H) shrink along one axis and belong to the boundary region of the tomato shoot apex shown in main Figure 4D, while the cells colored in red in (G) and (H) belong to the fast growing peripheral zone adajcent to the boundary. Scale bar 5 μm.
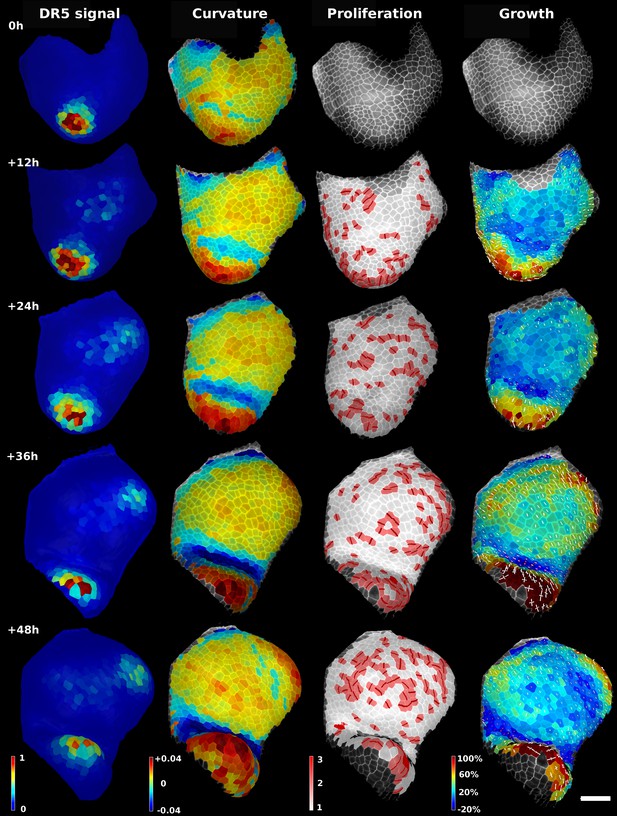
Analysis of time lapse series of tomato shoot apical growth over 48 hr (5 time points, 12 hr intervals).
First column on left: Quantification of pDR5::3xVENUS-N7 signal over 20 μm depth. Arbitrary units. Second column: Average tissue curvature for a neighborhood of 15 μm, given in μm−1. Third column: Cell proliferation, given in number of daughter cells. New cell walls are marked in dark red. Right column: Areal expansion (in %) for each 12 hr interval, displayed on the second time point. The axis of PDGs are displayed only for cells with high anisotropy. White axis represent expansion, red axis shrinkage. Scale bar: 50 μm.
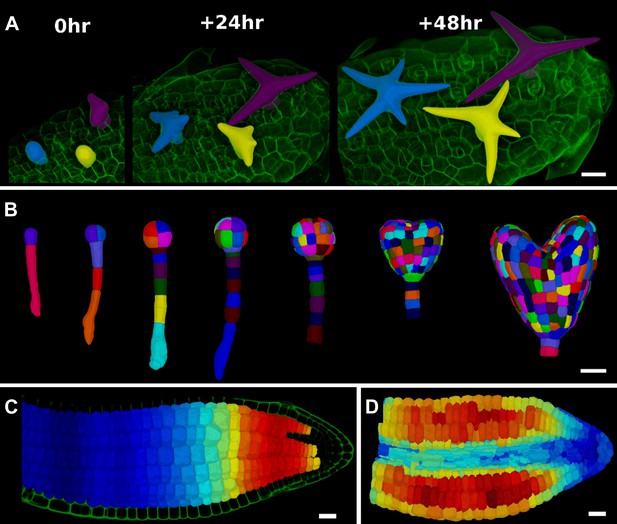
3D segmentation for growth tracking and modeling templates.
(A) Volume segmentation of trichomes from time-lapse confocal imaging in Capsella rubella leaf colored by cell label number. (B) Full 3D segmentation of developing Arabidopsis embryos, colored by cell label number. Data from (Yoshida et al., 2014). (C) False colored projection of the average growth rate along the main axis of an Arabidopsis embryo. Data from (Bassel et al., 2014). (D) Mechanical model of embryo based on a 3D mesh showing cell wall expansion due to turgor pressure, as published in (Bassel et al., 2014). Scale bars: 20 μm.
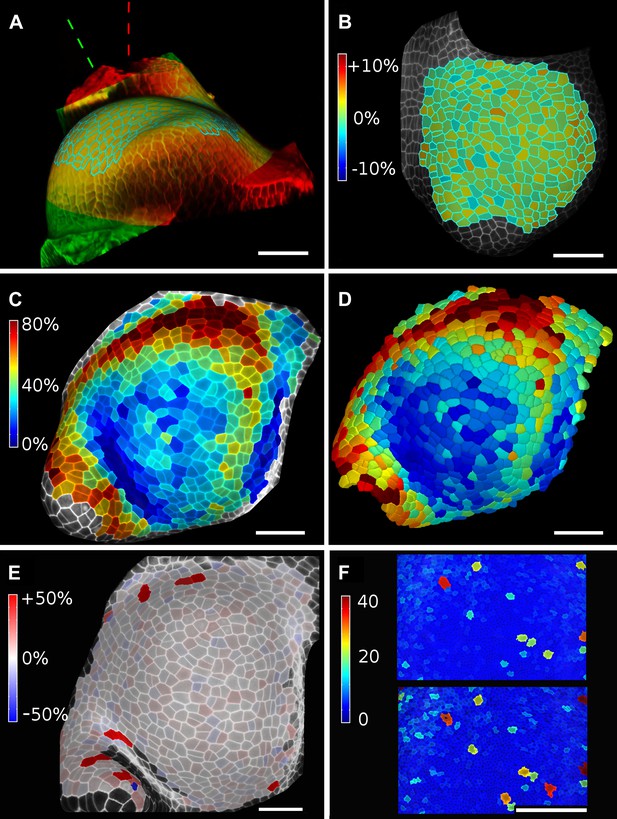
Validation of the method.
(A and B) Control for viewing angle. (A) A shoot apex imaged from different directions. A first image stack (in red) was acquired before tilting the Z axis (dashed lines) by approximately 30° and acquiring a second stack (in green). Cells were then segmented on both stacks and their areas compared (B). Note that the pairwise cell size differences are random, with no obvious trend related to the viewing angle. Average error per cell is less than 2%. Colorbar: relative surface area increase in percent. Panels (A) and (B) adapted from Figure 5 of Kierzkowski et al. (2012). (C and D) Comparison between projected areas and actual 3D volumes. (C) The epidermal cells of the apex were projected on the surface and segmented. Heatmap shows percent increase in area over 11 hr of growth. (D) The same data was segmented in 3D. Heatmap shows the percent increase in volume of cells, same color scale as in (C). Note the close correspondence in cell expansion extracted from surface and volumetric segmentations. (E) Difference in size between automatically and manually segmented cells on a tomato shoot apex. Cells fused by auto-segmentation are in bright red, split cells are in dark blue. (F) Cell sizes (in μm2) from manual (top) and automatic (bottom) segmentation on a fragment of Drosophila wing disc. Scale bars: 40 μm.
Videos
User interface and rendering in MorphoGraphX.
https://doi.org/10.7554/eLife.05864.005Manual segmentation of a tomato shoot apex.
https://doi.org/10.7554/eLife.05864.009Automatic segmentation of a tomato shoot apex.
https://doi.org/10.7554/eLife.05864.010Lineage tracking and growth analysis of time lapse data on tomato shoot apex.
https://doi.org/10.7554/eLife.05864.015Additional files
-
Supplementary file 1
MorphoGraphX User Manual. The MorphoGraphX user manual is written in a tutorial style, and the accompanying data sets are available for download on the MorphoGraphX website (www.MorphoGraphX.org). Installation instructions for MorphoGraphX and troubleshooting tips are in Section 16 towards the end of the manual.
- https://doi.org/10.7554/eLife.05864.022





