Noise promotes independent control of gamma oscillations and grid firing within recurrent attractor networks
- University of Edinburgh, United Kingdom
- Institute for Adaptive and Neural Computation, United Kingdom
Figures
Figure 1 with 1 supplement
Attractor network model with feedback inhibition and theta frequency inputs.
(A) A schematic of populations of excitatory cells (E cells, red) and inhibitory cells (I cells, blue) on a twisted torus of size 34 × 30 neurons. The synaptic coupling between the two populations was parameterized by the inter-population peak synaptic conductances gE (E → I synapses) and gI (I → E synapses). (B) Top: Plots illustrate peak synaptic conductances of E (red) and I (blue) synapses as a function of the distance between pre- and post-synaptic neurons. Bottom: Distributions of synaptic weights from all I cells onto an E cell in the model (left) and from all E cells onto an I-cell (right). Parameters gI and gE determine maximal values of these distributions. (C) Examples of the membrane potential of an isolated E cell during two consecutive theta cycles in networks without noise (white noise input current standard deviation σ = 0 pA), with an intermediate amount of noise (σ = 150 pA) and with noise levels doubled (σ = 300 pA). Theta signal is illustrated in grey.
Figure 1—figure supplement 1
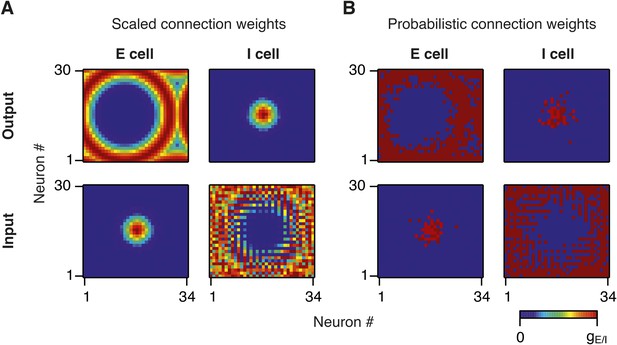
Synaptic weights in scaled and probabilistic variants of the network.
(A) Output (top) and input (bottom) synaptic weights of an E (left) and I (right) neuron in the middle of the twisted torus in a network in which synaptic weights are scaled according to the synaptic profile functions from Figure 1B. (B) Same as (A), but synaptic weights are constant and the probability of connection between a pair of neurons is scaled according to the synaptic profile functions in Figure 1B.
Figure 2 with 4 supplements
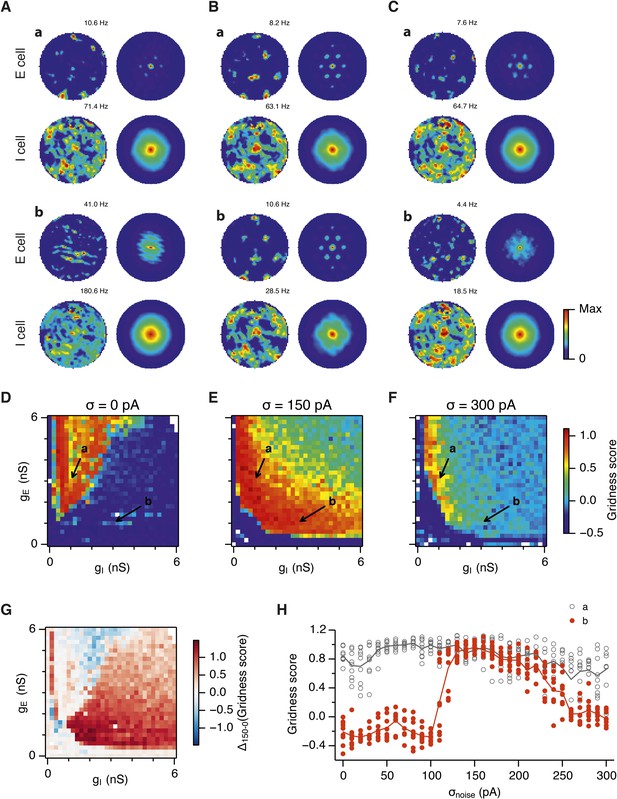
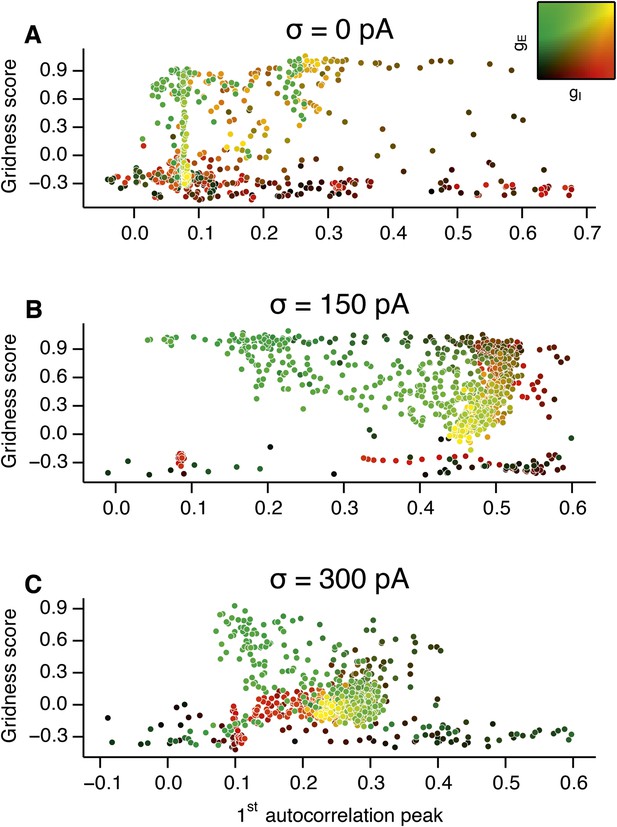
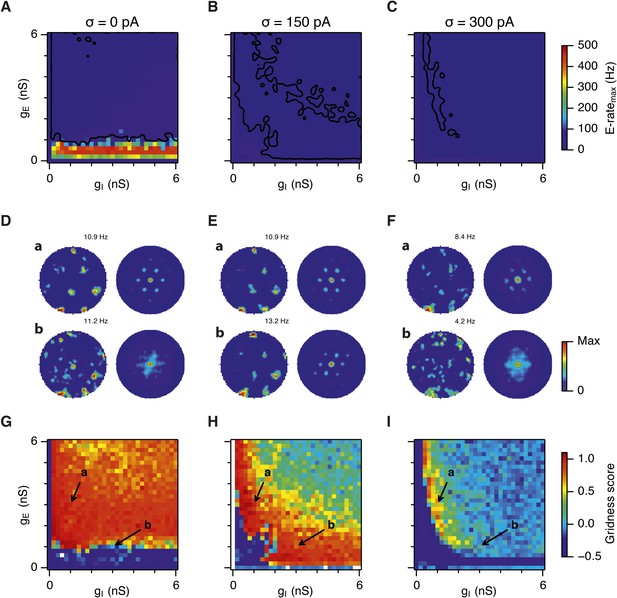
Noise increases the range of synaptic strengths that support grid firing.
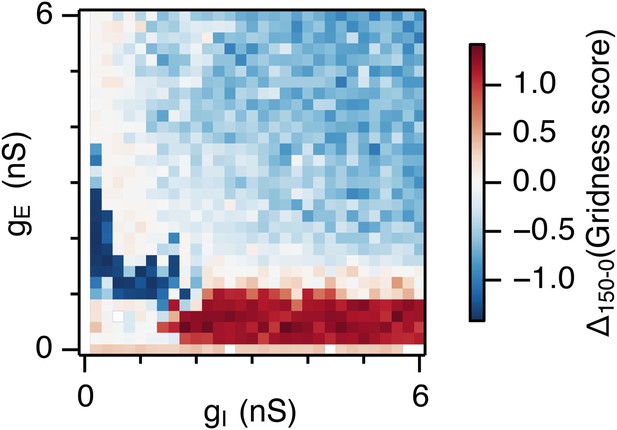
(A–C) Example spatial firing fields (left) and spatial autocorrelation plots (right) of E and I cells for networks without noise (A; σ = 0 pA), with noise level set to σ = 150 pA (B), and noise level set to σ = 300 pA (C) and with the strengths of recurrent synaptic connections indicated by arrows in (D–F). Maximal firing rate is indicated to the top right of each spatial firing plot. The range of spatial autocorrelations is normalized between 0 and 1. (D–F) Gridness score as a function of gE and gI for networks with each noise level. Each item in the color plot is an average gridness score of four simulation runs. Arrows indicate the positions of grid field and autocorrelation examples from simulations illustrated in (A–C). Simulations that did not finish in a specified time interval (5 hr) are indicated by white color. (G) Difference between gridness scores of networks with σ = 150 pA and networks with σ = 0 pA plotted as a function of gE and gI. (H) Gridness score plotted as a function of the standard deviation of intrinsic noise. Each noise level comprises simulations from a neighborhood of gE and gI surrounding a center point in the parameter space (center included) indicated by arrows in (D–F).
Figure 2—figure supplement 1
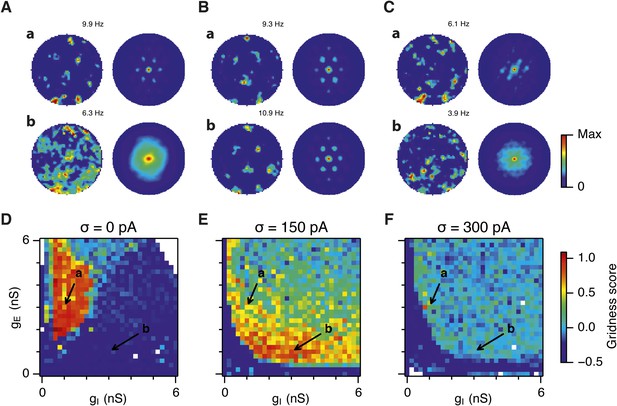
Sensitivity of grid firing to changes in feedback inhibition, excitation and noise levels in networks with connection probability between pairs of neurons drawn according to the synaptic profile functions in Figure 1B.
(A–C) Example spatial firing fields (left) and spatial autocorrelation plots (right) of E and I cells for networks without noise (A; σ = 0 pA), with noise set to σ = 150 pA (B), and noise set to σ = 300 pA (C) and with the strengths of recurrent synaptic connections indicated by arrows in (D–F). Maximal firing rate is indicated in the top right of each spatial firing plot. The range of spatial autocorrelations is normalized between 0 and 1. (D–F) Gridness score as a function of gE and gI for networks with each noise level. Each item in the color plot is an average gridness score of two simulation runs. Arrows indicate the positions of grid field and autocorrelation examples from simulations illustrated in (A–C). Simulations that did not finish in a specified time interval (5 hr) are indicated by white color.
Figure 2—figure supplement 2
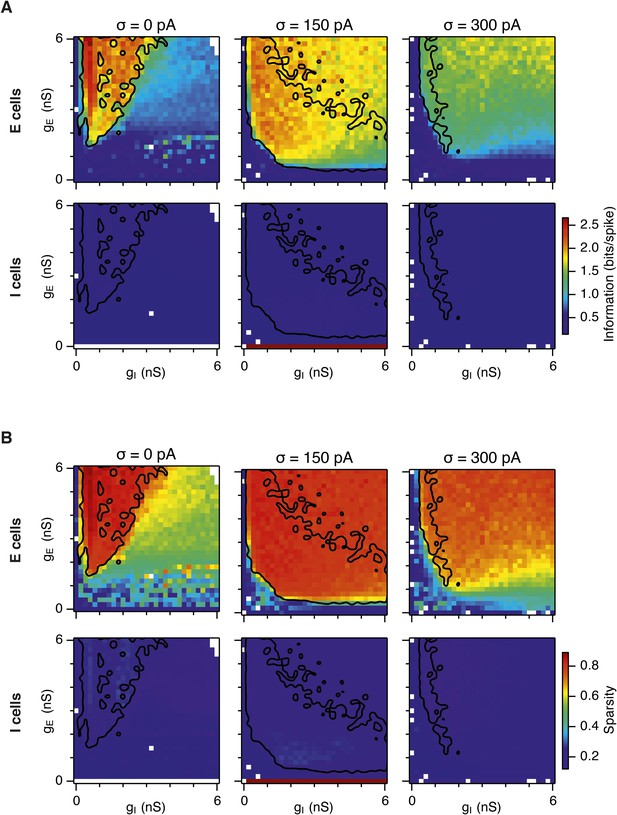
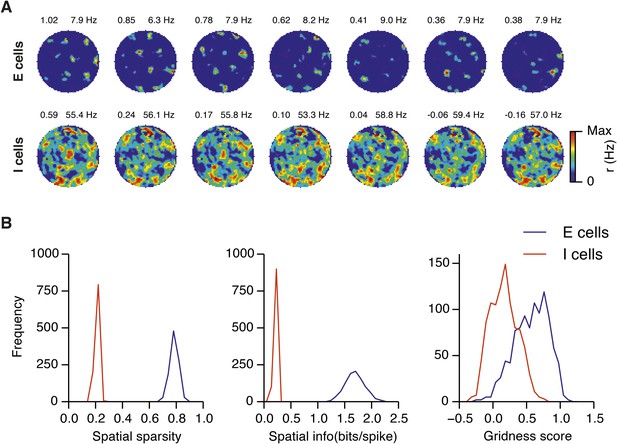
Spatial information and sparsity of firing fields of E and I cells.
(A) Spatial information of E (top) and I (bottom) cells as a function of gE and gI in networks from Figure 2. (B) Same as (A), but the color plots show spatial sparsity of E and I cells. Black lines indicate the region from Figure 2D–F where the gridness score = 0.5.
Figure 2—figure supplement 3
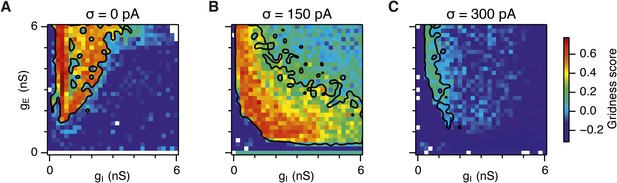
Gridness scores of I cells.
Colour plots show gridness score as a function of gE and gI for networks without noise (A), with noise standard deviation σ = 150 pA (B), and σ = 300 pA (C). Data are from simulations of networks with feedback inhibition only (E-I networks; Figure 2). Black lines indicate the region from Figure 2D–F where the gridness score of E cells = 0.5.
Figure 2—figure supplement 4
Spatial firing fields in networks with uncorrelated spatial input applied to each I cell.
(A) Examples of firing fields of E and I cells. Gridness score and maximal firing rate of the firing field is indicated in the top left and right parts of each firing field, respectively. (B) Distributions of spatial sparsity (left), spatial information (centre) and gridness score (right) of 100 randomly selected cells from each population of neurons. Each simulation run was repeated 10 times with different random seeds. Network parameters were gE = 3 nS and gI = 1 nS. Each I cell received connections from three randomly selected neurons with a place like spatial firing field. Properties of place cells: rmax = 100 Hz, σfield = 80 cm (cf. Appendix 1).
Figure 3 with 4 supplements
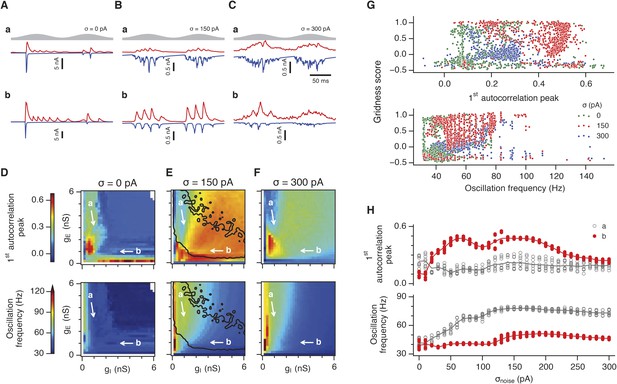
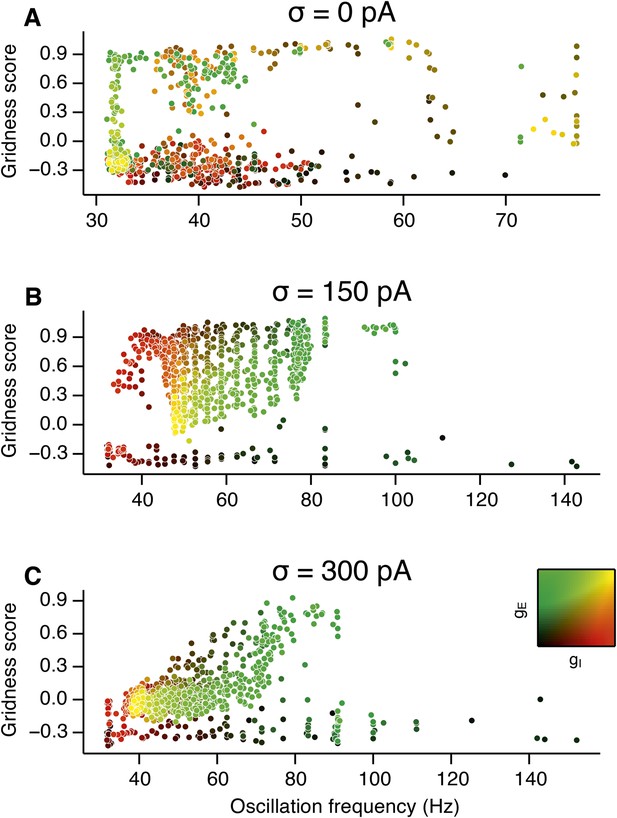
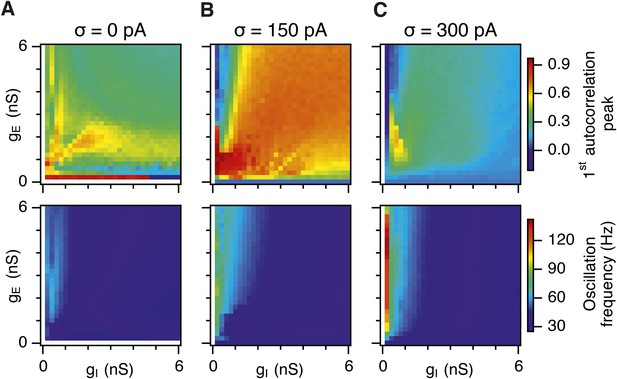
Differential sensitivity of gamma oscillations and grid fields to changes in the strength of E and I synapses.
(A–C) Examples of inhibitory (red) and excitatory (blue) synaptic currents recorded respectively from excitatory and inhibitory neurons from simulations highlighted by arrows in panels (D–F). (D–F) Top: Correlation value at the first local maximum of the autocorrelation of inhibitory synaptic currents (I → E cells, 25 randomly selected E cells), plotted as a function of gE and gI, for networks without noise (D), with noise level set to σ = 150 pA (E), and noise level set to σ = 300 pA (F). Each point is an average over five simulation trials. In these simulations velocity and place cell inputs were disabled. The duration of simulations was 10 s. Bottom: Frequency corresponding to the peaks of the autocorrelation functions for simulations in the top panels. Black lines in (E) indicate the region from Figure 2E where the gridness score = 0.5. (G) Scatter plots show gridness score as a function of gamma oscillation strength (top) and frequency (bottom) for simulations with noise absent (green), with an intermediate level of noise (red) and highest simulated noise level (blue). Each dot represents data from a single network configuration. (H) Top: Gamma oscillation strength plotted as a function of standard deviation of the noise current. Grey color indicates simulations with gE = 3 nS, gI = 1 nS (A). Red color indicates simulations with gE = 1 nS, gI = 3 nS (B). Bottom: Frequency corresponding to the detected autocorrelation peak.
Figure 3—figure supplement 1
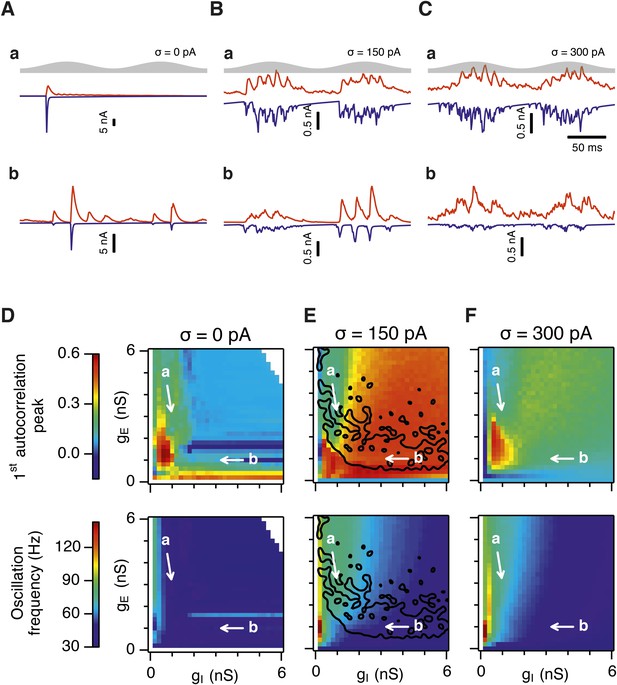
Sensitivity of gamma oscillations to changes in the strength of E and I synapses in networks with connection probability between pairs of neurons drawn according to the synaptic profile functions in Figure 1B.
(A–C) Examples of inhibitory (red) and excitatory (blue) synaptic currents recorded respectively from excitatory and inhibitory neurons from simulations highlighted by arrows in panels (D–F). (D–F) Top: Correlation value at the first local maximum of an autocorrelation of inhibitory synaptic currents (I → E cells, 25 randomly selected E cells), plotted as a function of gE and gI, for networks without noise (D), with noise set to σ = 150 pA (E), and noise set to σ = 300 pA (F). Each point is an average over five simulation trials. In these simulations velocity and place cell inputs were disabled. The duration of simulations was 10 s. Bottom: Frequency corresponding to the peaks of the autocorrelation functions for simulations in the top panels. Black lines in (E) indicate the region from Figure 2—figure supplement 1 where the gridness score = 0.5.
Figure 3—figure supplement 2
Scatter plots of gridness score as a function of the amplitude of gamma oscillations.
(A–C) The plots show relationships between grid field computations (gridness score) and the power of nested gamma oscillations for deterministic networks (A), networks with moderate noise (B) and networks with the highest simulated noise level (C). Noise level is indicated by σ. The strength of the oscillation was obtained by computing autocorrelation functions of inhibitory currents impinging onto 25 randomly selected E cells in the network and detecting their first local maxima. The correlation value at the first local maximum is plotted on the abscissa. Color coding determines the values of gE and gI, as shown in the 2D colorbar.
Figure 3—figure supplement 3
Scatter plots of gridness score as a function of the detected oscillation frequency.
(A–C) The plots show relationships between grid field computations (gridness score) and the frequency of gamma oscillations for deterministic networks (A), networks with moderate noise (B) and networks with the highest simulated noise level (C). Noise level is indicated by σ. The frequency of the oscillation was obtained by computing autocorrelation functions of inhibitory currents impinging onto 25 randomly selected E cells in the network and detecting their first local maxima. The time lag at the first local maximum yielded the frequency of the oscillation, which is plotted on the abscissa. Color coding determines the values of gE and gI, as shown in the 2D colorbar.
Figure 3—figure supplement 4
Amplitude and frequency of gamma oscillations in the gE and gI parameter regions where grid fields are robust.
Amplitude (top) and frequency (bottom) of detected gamma oscillations for simulations in which gridness score is greater than 0.5, in deterministic networks (A), networks with an intermediate level of noise (B) and in networks with the highest simulated level of noise (C). The data in this figure are from simulations in Figure 3.
Figure 4 with 1 supplement
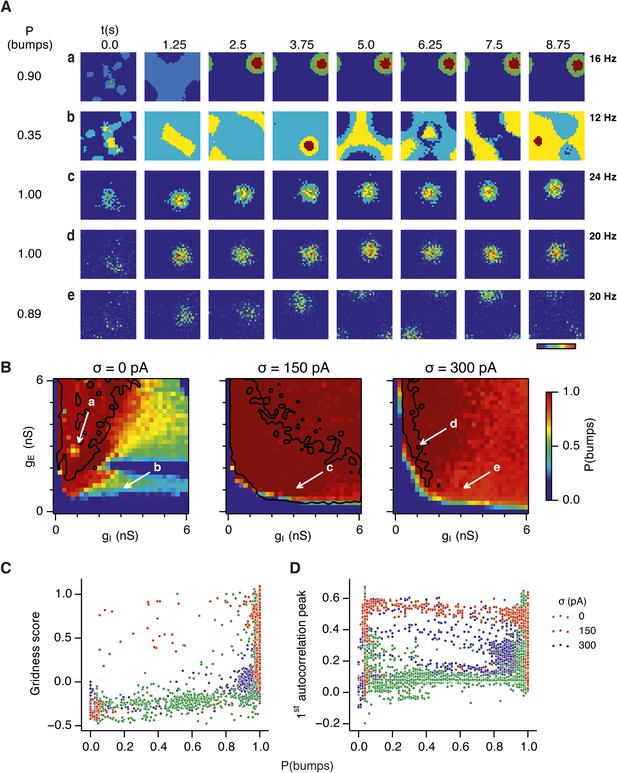
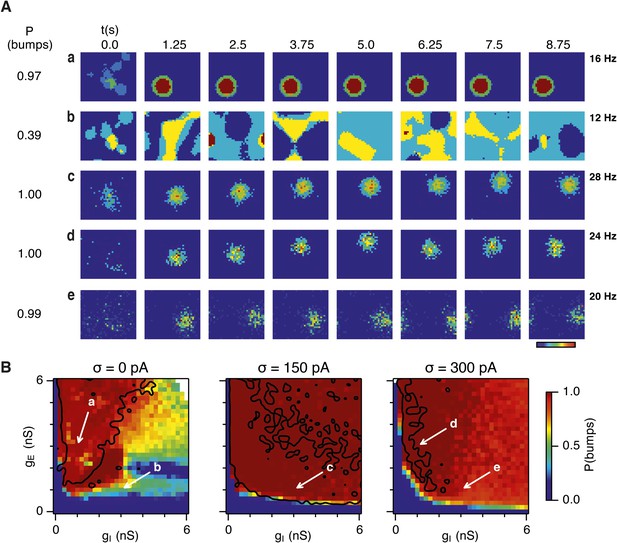
Noise promotes formation of continuous attractors.
(A) Examples of snapshots of network activity of E cells from simulations in which velocity and place cell inputs are inactivated. Each row shows a simulation trial with a value of gE and gI highlighted by an arrow in panel (B). The corresponding probability of bump formation (P(bumps)) and the maximal firing rate is indicated to the left and right, respectively. (B) Color plots show probability of bump formation (P(bumps)), for the simulated range of gE and gI and the three simulated noise levels. Each color point is an average of five 10 s simulation runs. Arrows show positions in the parameter space of examples in (A). Black lines indicate the regions where the gridness score = 0.5 (cf. Figure 2D–F). (C) Relationship between gridness score computed from the grid field simulation runs (Figure 2D–F) and the probability of bump formation (B). (D) Relationship between gamma oscillation strength (Figure 3D–F) and the probability of bump formation (B). Each color in (C and D) represents one noise level and each dot in the scatter plots corresponds to simulations of a single pair of values of gE and gI.
Figure 4—figure supplement 1
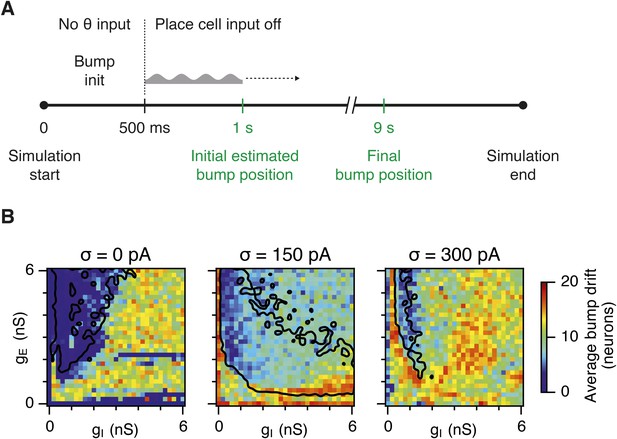
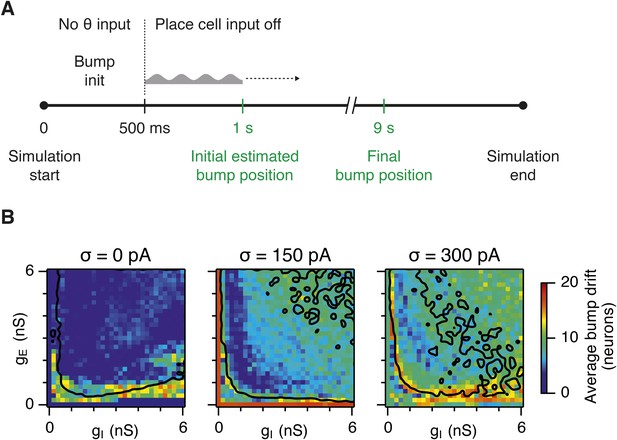
Sensitivity of bump attractor spontaneous drift to variations in gE and gI and noise levels.
(A) Schematic of the bump attractor drift estimation procedure. The first 500 ms of a simulation trial are used to initialize the bump attractor. Onset of theta modulated input current was at 500 ms. The estimated centers of bump attractors measured by the least squares fit of symmetric Gaussians were at 1 s (initial position) and 9 s (final position). The drift was then estimated as the distance on twisted torus between the initial and final position. Simulation time was 10 s. (B) Color plots show bump attractor drifts averaged over five simulation trials, for the simulated ranges of excitatory and inhibitory synaptic strengths and levels of noise. Networks without noise can form stable bump attractors in a subset of their parameter region. Networks with noise suffer from attractor drift in majority of the parameter region. Black lines in (B) indicate the region from Figure 2D–F where gridness score = 0.5.
Figure 5 with 1 supplement
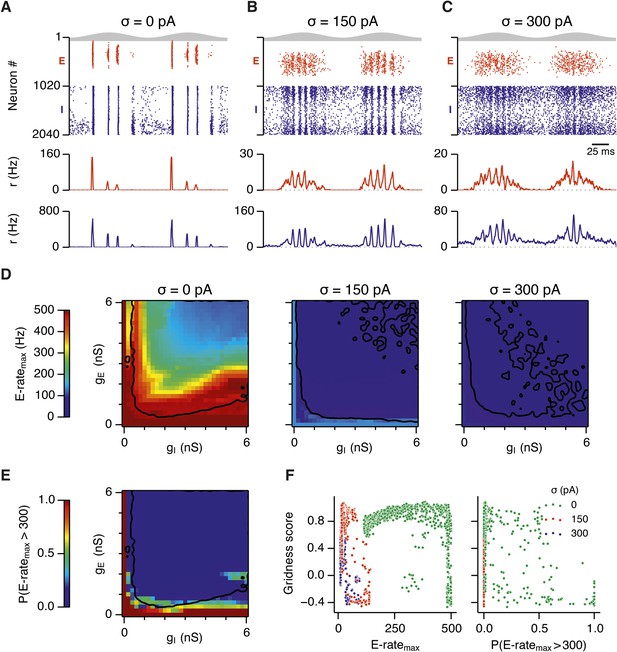
Noise opposes generation of seizure-like states.
(A–C) Raster plots show activity of all neurons in the excitatory (red) and inhibitory (blue) populations for the duration of two theta cycles (top), along with the average population firing rates for both populations (center and bottom; calculated with a sliding rectangular window with 2 ms duration and 0.5 ms time step), for networks where noise is absent (A; σ = 0), with noise set to σ = 150 pA (B), and with noise set to σ = 300 pA (C). Simulations were performed in the absence of animal movement and place cell input; gE = 1 nS and gI = 3 nS. (D) Maximal average population firing rate of E cells estimated from the whole simulation run (10 s; 500 ms at the beginning of the simulation excluded) for each simulated level of noise. Each point is an average of maxima from five simulation runs. (E) Probability of the maximal population-average firing rate during each theta cycle exceeding 300 Hz, that is, at least 60% of E cells firing synchronously within a time period of 2 ms in the parameter space of gE and gI when σ = 0 pA. Black lines indicate regions where gridness score equals 0.5. (F) Scatter plots show the relationship between gridness score and the maximal firing rate during the simulation (left) and the probability of the maximal population-average firing rate during each theta cycle exceeding 300 Hz (right).
Figure 5—figure supplement 1
Examples of activity in the network.
(A–C) Top: Mean maximal firing rate per theta cycle (average over five trials), outlining the average activity during theta cycles, in the parameter space of gE and gI. Center and bottom: Raster plots (center) and population-average firing rates (bottom) of all cells in selected locations of the E-I parameter space during 16 consecutive θ cycles. Action potentials and firing rates of E and I cells are colored red and blue, respectively. An arrow highlights the position in the parameter space.
Figure 6 with 5 supplements
Seizure-like states and grid firing fields in networks without theta frequency inputs.
(A–C) Maximal average population firing rate of E cells estimated from the whole simulation run (10 s; 500 ms at the beginning of the simulation excluded) for each simulated level of noise indicated by σ, in networks with theta frequency inputs replaced with a constant input with the same mean amplitude. Each point is an average of maxima from five simulation trials. Black lines indicate the regions from (G–H) where gridness score = 0.5. (D–F) Example spatial firing fields (left) and autocorrelation plots (right) for the specific values of gE and gI indicated by arrows in (G–I), corresponding to the three simulated noise levels. Maximal firing rate is indicated at the top right of each spatial firing plot. The range of spatial autocorrelations is normalized between 0 and 1. (G–I) Gridness score as a function of gE and gI, for each simulated level of noise. Each item in the color plot is an average gridness score of three simulation runs of 600 s duration. Arrows indicate the positions of grid field and autocorrelation examples from simulations illustrated in (D–F). Simulations that did not finish in a specified time interval (5 hr) are indicated by white color.
Figure 6—figure supplement 1
Effect of replacing theta frequency inputs by a constant input with an equal mean amplitude.
(A–C) Amplitude (top) and frequency (bottom) of detected gamma oscillations (‘Materials and methods’) in deterministic networks (A), networks with an intermediate level of noise (B) and in networks with the highest simulated level of noise (C). Each point is an average of five simulation runs. Data are from the same simulation set. White color indicates simulation runs in which no autocorrelation peaks were detected (cf. ‘Materials and methods’).
Figure 6—figure supplement 2
Effect of noise on gridness scores in networks without theta frequency inputs.
The plot shows a difference between gridness scores of networks with σ = 150 pA and networks with σ = 0 pA plotted as a function of gE and gI when theta inputs were replaced with a constant input with an equal mean amplitude.
Figure 6—figure supplement 3
Firing rates of E cells.
(A) Average firing rate of all E cells during simulations of animal movement as a function of gE and gI. Black lines outline the region from Figure 2D–F where gridness score = 0.5. (B) Relationship between gridness score and firing frequency of E cells.
Figure 6—figure supplement 4
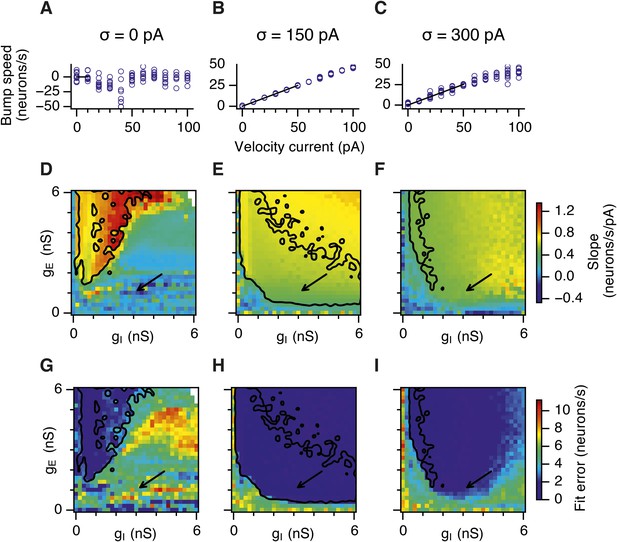
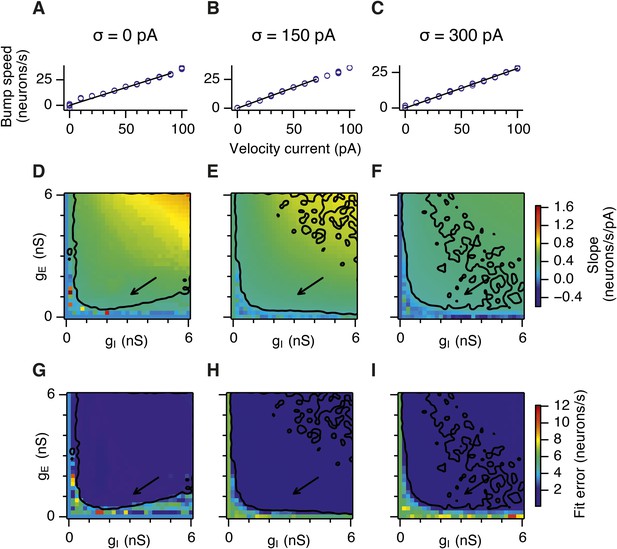
Calibration of the gain of the velocity inputs.
(A–C) Bump attractor speed as a function of the strength of the velocity current for the three simulated levels of noise. 10 simulation runs were performed for each level of noise (blue markers). In each run the speed of the bump was calculated in response to the injected velocity input and the data were used to fit a linear relationship using an estimation procedure outlined in Appendix 1 (black line). (D–F) Slope of the estimated velocity gain of the attractor networks as a function of gE and gI for all simulated levels of noise. (G–I) Same as in (D–F) but the plots show error of fit for the estimated linear relationships. Arrows show locations of the data plotted in (A–C). Black lines in (D–I) indicate the region from Figure 2D–F where gridness score = 0.5.
Figure 6—figure supplement 5
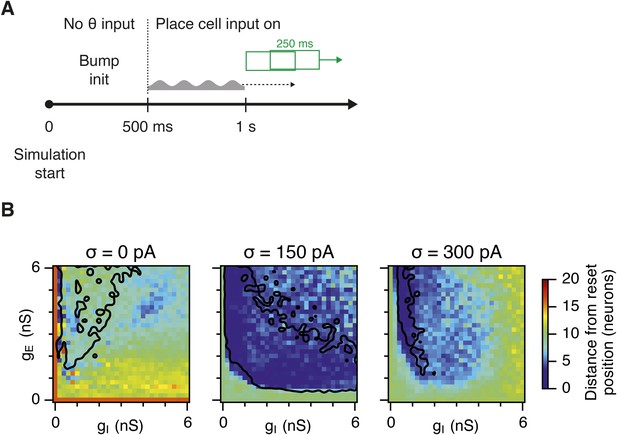
Effectivity of the place cell resetting mechanism as a function of gE and gI and noise levels.
(A) Illustration of the procedure to estimate the difference between the bump position induced by place cells and actual estimated position of the bump state, by using a sliding window with 250 ms duration and 125 ms time step. The resulting distance from the reset position, in one simulation run, was then an average over all sliding windows. (B) Color plots show the effectivity of place cell mechanism for an average of five simulation runs with 10 s duration. Place cells are most effective in networks with an intermediate amount of noise. Black lines in (B) indicate the region from Figure 2D–F where gridness score = 0.5.
Figure 7 with 10 supplements
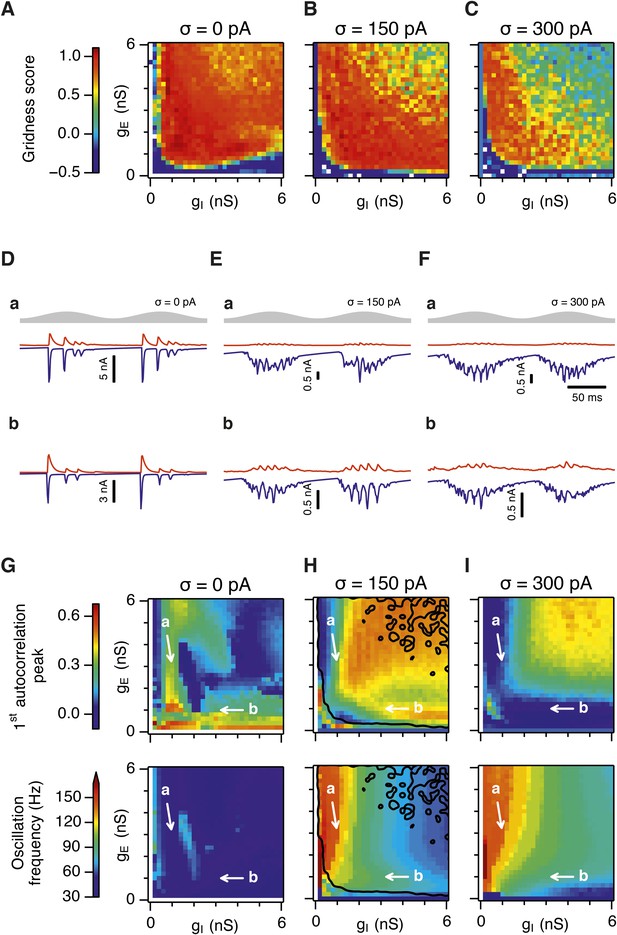
Gridness scores and gamma activity in networks with recurrent inhibition.
(A–C) Gridness score as a function of gE and gI for networks without noise (A; σ = 0 pA), with noise level set to σ = 150 pA (B), and noise level set to σ = 300 pA (C). Simulations that did not finish in a specified time interval (5 hr) are indicated by white color. (D–F) Examples of inhibitory (red) and excitatory (blue) synaptic currents recorded respectively from excitatory and inhibitory neurons from simulations highlighted by arrows in panels (G–I). (G–I) Top: Correlation value at the first local maximum of an autocorrelation of inhibitory synaptic currents (I → E cells, 25 randomly selected E cells), plotted as a function of gE and gI, for networks without noise (G), with noise level set to σ = 150 pA (H), and noise level set to σ = 300 pA (I). Each point is an average over five simulation trials. In these simulations velocity and place cell inputs were disabled. The duration of simulations was 10 s. Bottom: Frequency corresponding to the peaks of the autocorrelation functions for simulations in the top panels. Black lines in (H) indicate the regions from (B) where gridness score = 0.5.
Figure 7—figure supplement 1
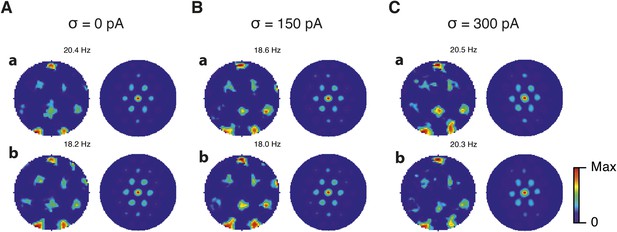
Spatial firing fields in networks that contain recurrent I → I synapses.
(A–C) Example spatial firing fields (left) and spatial autocorrelation plots (right) for networks with gE = 3 nS and gI = 1 nS (A) and networks with gE = 1 nS and gI = 3 nS (B), corresponding to the three simulated noise levels indicated by σ. Maximal firing rate is indicated to the top right of each spatial firing plot. Range of spatial autocorrelations is normalized between 0 and 1.
Figure 7—figure supplement 2
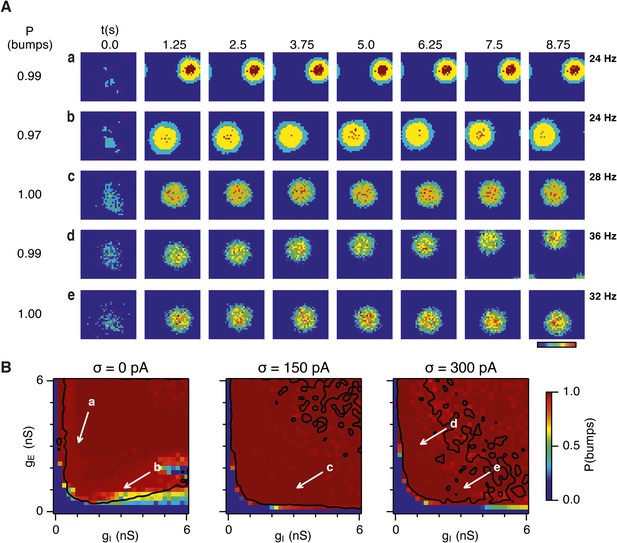
Continuous attractors in networks that contain direct I → I synapses.
(A) Examples of E cell population firing rate snapshots from simulations in which velocity and place cell inputs are inactivated. Each row shows a simulation trial with a value of gE and gI highlighted by an arrow in panel (B). The corresponding probability of bump formation (P(bumps)) is indicated to the left. Maximal firing rate for each set of snapshots is indicated to the right. (B) Color plots show probability of bump formation (P(bumps)), for the simulated range of gE and gI and the three simulated noise levels. Each color point is an average of five 10 s simulation runs. Black lines in (B) indicate the region from Figure 7A–C where gridness score = 0.5.
Figure 7—figure supplement 3
Sensitivity of bump attractor spontaneous drift to variations in gE, gI and noise levels in networks that contain direct I → I synapses.
(A) Schematic of the bump attractor drift estimation procedure. The first 500 ms of a simulation trial are used to initialize the bump attractor. Onset of theta modulated input current was at 500 ms. The estimated centers of bump attractors measured by the least squares fit of symmetric Gaussians were at 1 s (initial position) and 9 s (final position). The drift was then estimated as the distance on twisted torus between the initial and final position. Simulation time was 10 s. (B) Color plots show bump attractor drifts averaged over five simulation trials, for the simulated ranges of excitatory and inhibitory synaptic strengths and levels of noise. Networks without noise can form stable bump attractors in a subset of their parameter region. Networks with noise suffer from attractor drift in the majority of the parameter region. Black lines in (B) indicate the region from Figure 7A–C where gridness score = 0.5.
Figure 7—figure supplement 4
Calibration of the gain of the velocity inputs in networks that contain direct I → I synapses.
(A–C) Bump attractor speed as a function of the strength of the velocity current for the three simulated levels of noise indicated by σ. Values of gE and gI are indicated by arrows in (D–I). 10 simulation runs were performed for each level of noise (blue markers). In each run the speed of the bump was calculated in response to the injected velocity input and the data were used to fit a linear relationship using an estimation procedure outlined in Appendix 1 (black line). (D–F) Slope of the estimated velocity gain of the attractor networks as a function of gE and gI for all simulated levels of noise. (G–I) Same as in (D–F) but the plots show error of fit for the estimated linear relationships. Arrows in (D–I) show locations of the data plotted in (A–C). Black lines in (D–I) indicate the region from Figure 7A–C where gridness score = 0.5.
Figure 7—figure supplement 5
Seizure-like states in networks that contain direct I → I synapses.
(A–C) Raster plots show activity of all neurons in the excitatory (red) and inhibitory (blue) populations for the duration of two theta cycles (top), along with the average population firing rates for both populations (center and bottom; calculated with a sliding rectangular window with 2 ms duration and 0.5 ms time step), for networks where noise is absent (A; σ = 0), with noise set to σ = 150 pA (B), and with noise set to σ = 300 pA (C). Simulations were performed in the absence of animal movement and place cell input; gE = 1 nS and gI = 3 nS. (D) Maximal average population firing rate of E cells estimated from the whole simulation run (10 s; 500 ms at the beginning of the simulation excluded) for each simulated level of noise. Each point is an average of maxima from five simulation runs. (E) Probability of the maximal population-average firing rate during each theta cycle exceeding 300 Hz, that is, at least 60% of E cells firing synchronously within a time period of 2 ms, in the parameter space of gE and gI when σ = 0 pA. Black lines indicate the regions from Figure 7A–C where gridness score equals 0.5. (F) Scatter plots show the relationship between gridness score and the maximal firing rate during the simulation (left) and the probability of the maximal population-average firing rate during each theta cycle exceeding 300 Hz (right).
Figure 7—figure supplement 6
Sensitivity of grid firing to changes in inhibition and excitation in networks that contain direct E → E synapses.
(A–C) Example firing fields (left) and spatial autocorrelation plots (right) for the strengths of recurrent synaptic connections indicated by arrows in (D–F) for networks without noise (A; σ = 0 pA), with noise set to σ = 150 pA (B), and noise set to σ = 300 pA (C). (D–F) Gridness score as a function of gE and gI for networks with each noise level. Each item in the color plot is an average gridness score of two simulation runs. Arrows indicate the positions of grid field and autocorrelation examples from simulations illustrated in (A–C).
Figure 7—figure supplement 7
Sensitivity of gamma oscillations to changes in inhibition and excitation in networks that contain direct E → E synapses.
(A–C) Examples of inhibitory (red) and excitatory (blue) synaptic currents recorded respectively from excitatory and inhibitory neurons from simulations highlighted by arrows in panels (D–F). (D–F) Top: Correlation value at the first local maximum of an autocorrelation of inhibitory synaptic currents (I → E cells, 25 randomly selected E cells), plotted as a function of gE and gI, for networks without noise (D), with noise set to σ = 150 pA (E), and noise set to σ = 300 pA (F). Each point is an average over five simulation trials. In these simulations velocity and place cell inputs were disabled. The duration of simulations was 10 s. Bottom: Frequency corresponding to the peaks of the autocorrelation functions for simulations in the top panels. Black lines in (E) indicate the region from Figure 7—figure supplement 6 where the gridness score = 0.5.
Figure 7—figure supplement 8
Continuous attractors in networks that contain direct E → E synapses.
(A) Examples of E cell population firing rate snapshots from simulations in which velocity and place cell inputs are inactivated. Each row shows a simulation trial with a value of gE and gI highlighted by an arrow in panel (B). The corresponding probability of bump formation (P(bumps)) is indicated to the left. Maximal firing rate for each row is indicated to the right. (B) Color plots show probability of bump formation (P(bumps)), for the simulated range of gE and gI and the three simulated noise levels indicated by σ. Each color point is an average of five 10 s simulation runs. Arrows show positions in the parameter space of examples in (A). Black lines indicate the region from Figure 7—figure supplement 6 where the gridness score = 0.5.
Figure 7—figure supplement 9
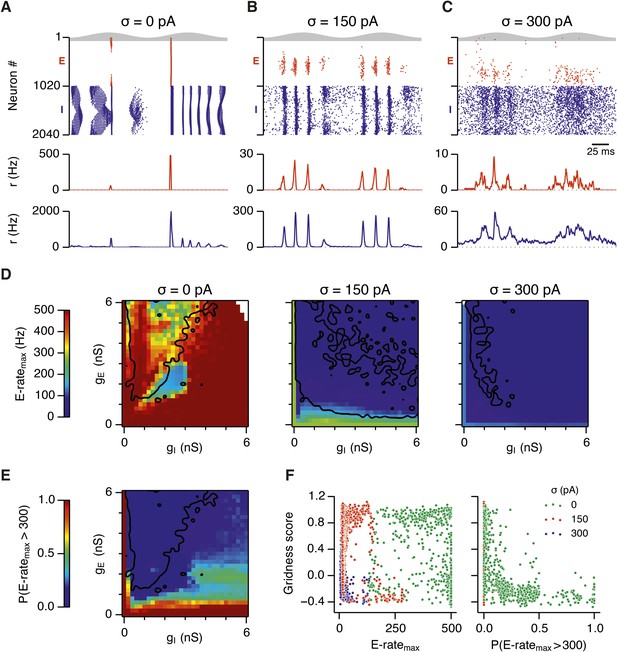
Seizure-like states in networks that contain direct E → E synapses.
(A–C) Raster plots show activity of all neurons in the excitatory (red) and inhibitory (blue) populations for the duration of two theta cycles (top), along with the average population firing rates for both populations (center and bottom; calculated with a sliding rectangular window with 2 ms duration and 0.5 ms time step), for networks where noise is absent (A; σ = 0), with noise set to σ = 150 pA (B), and with noise set to σ = 300 pA (C). Simulations were performed in the absence of animal movement and place cell input; gE = 1 nS and gI = 3 nS. (D) Maximal average population firing rate of E cells estimated from the whole simulation run (10 s; 500 ms at the beginning of the simulation excluded) for each simulated level of noise. Each point is an average of maxima from five simulation runs. (E) Probability of the maximal population-average firing rate during each theta cycle exceeding 300 Hz, that is, at least 60% of E cells firing synchronously within a time period of 2 ms in the parameter space of gE and gI when σ = 0 pA. (F) Scatter plots show the relationship between gridness score and the maximal firing rate during the simulation (left) and the probability of the maximal population-average firing rate during each theta cycle exceeding 300 Hz (right). Black lines in (D and E) indicate the region from Figure 7—figure supplement 6 where the gridness score = 0.5.
Figure 7—figure supplement 10
Probability of bump formation and network activity plots in networks with structured E → E and unstructured E → I and I → E connections.
Since the presence of bump attractors is necessary for grid computation, we tested whether networks with only structured E-E connections can generate activity bumps. We used the Gaussian fitting procedure (cf. ‘Materials and methods’) to estimate the presence of bump attractors in these networks. (A) Probability of bump formation as a function of the E-E synaptic scaling factor (gE → E) and the width of the synaptic profile (σE → E). Arrow highlights the position in the parameter space corresponding to the raster plots (center) and network activity snapshots (bottom) for E and I cells. Firing rate in the network activity color plots are in the range of 0 (dark blue) to the maximum firing rate indicated to the right of the plot (dark red). In these networks gE = 1 nS and gI = 0.1 nS. (B) Same as (A) but gE = 3 nS and gI = 1 nS. (C) Same as (A) and (B) but in these simulations the synaptic scaling factor of E-E connections and the width of the synaptic profile were fixed (gE → E = 3 nS and σE → E = 0.0833) and gE and gI varied in the range of 0–6 nS. Simulations that produced excessive spiking activity and did not finish in a specified time limit (3 hr) are indicated by white color. Many networks suffer from runaway excitation and inhibition (A) or generate only background synaptic activity characterized by low firing rates of E and I cells (B and C). The Gaussian fitting procedure used to estimate the probability of bump formation can nevertheless yield a high bump score due to the fact that this procedure can also give a high score to intermittent pockets of activity (A) or pockets of background activity of E cells (B and C). This activity, however, is not stable enough to generate grid firing fields.
Appendix figure 1
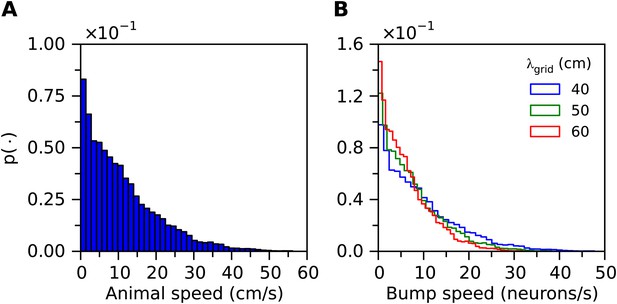
(A) Histogram of velocities of a simulated animal.
(B) Histogram of bump speeds derived from the animal velocities estimated in Equation 21, for different grid field spacings.
Tables
Appendix table 1
Parameter values for synapses
| Name | Units | Value |
|---|---|---|
| EAMPA | mV | 0 |
| τAMPA | ms | 1 |
| ENMDA | mV | 0 |
| τNMDA | ms | 100 |
| mV | −75 | |
| ms | 5 |
Appendix table 2
Neuron parameters and their description
| Name | Description | Name | Description |
|---|---|---|---|
| Vm | Membrane potential | EAMPA | AMPA reversal potential |
| Cm | Membrane capacitance | gNMDA | NMDA conductance |
| gL | Leak conductance | ENMDA | NMDA reversal potential |
| EL | Leak reversal potential | Im | Trans-membrane current |
| gAHP | AHP conductance | Isyn | Synaptic current |
| τAHP | AHP time constant | Isyn | Synaptic current |
| EAHP | AHP reversal potential | Iext | External current |
| ΔT | Spike initiation width | Iconst | Constant current |
| VT | Spike initiation threshold | Iθ | Theta-modulated current |
| GABA conductance | Ivel | Velocity current | |
| GABA reversal potential | Iplace | Place cell current | |
| gAMPA | AMPA conductance | τAMPA | AMPA time constant |
| GABA time constant | τNMDA | NMDA time constant | |
| gad | Adaptation conductance | τad | Adaptation time constant |
| AHP maximal value | Adaptation conductance increase | ||
| Aθ | θ-current amplitude | fθ | θ-current frequency |
| ϕθ | θ-current phase | – | – |
| wAMPA | AMPA synaptic weight | wNMDA | NMDA synaptic weight |
| GABA synaptic weight | – | – |
-
For the exact values used in the simulations, refer to Appendix tables 1, 3–5.
Appendix table 3
Single neuron parameter values for all cells
| Name | Units | Value (E cells) | Value (I cells) |
|---|---|---|---|
| Cm | pF | 211.389 | 227.3 |
| EL | mV | −68.5 | −60 |
| VT | mV | −50 | −45 |
| Vr | mV | −68.5 | −60 |
| gL | nS | 22.73 | 22.73 |
| ΔT | mV | 0.4 | 0.4 |
| EAHP | mV | −80 | × |
| τAHP | ms | 20 | × |
| nS | 5 | × | |
| τad | ms | × | 7.5 |
| nS | × | 22.73 |
Appendix table 4
Parameter values for external inputs
| Name | Units | Value (E cells) | Value (I cells) |
|---|---|---|---|
| Iconst | pA | 300 | 200 |
| Aθ | pA | 375 | 25 |
| ϕθ | rad | −π/2 | −π/2 |
| fθ | Hz | 8 | 8 |
Appendix table 5
Parameter values for synaptic profiles
| Name | Units | Value |
|---|---|---|
| μ | normalised | 0.433 |
| σexc | normalised | 0.0834 |
| σinh | normalised | 0.0834 |
| C | normalised | 0.03 |
| λgrid | cm | 60 |
Additional files
-
Supplementary file 1
Examples of spatial firing fields. (A-L) Top: Gridness score in the parameter space of the E and I synaptic strength scaling parameters (gE and gI respectively). Bottom: Firing fields of a single cell obtained by simulating animal movement, in the parameter region highlighted by black rectangle in the parameter space plot. Above each firing field is the estimated gridness score (left) and maximal firing rate in the firing field (right). Blank (white) locations in the parameter space are simulations that did not finish in the pre-specified time limit (5 hr). Noise level used in each set of simulations is shown by σnoise. Color scale in the firing field plots ranges from 0 Hz (dark blue) to the maximal firing rate for each of the firing fields (dark red).
- https://doi.org/10.7554/eLife.06444.036
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Noise promotes independent control of gamma oscillations and grid firing within recurrent attractor networks
eLife 4:e06444.
https://doi.org/10.7554/eLife.06444
