Optogenetic feedback control of neural activity
- Massachusetts Institute of Technology, United States
- Georgia Institute of Technology, United States
- Emory University School of Medicine, United States
- Axion Biosystems, United States
Figures
Figure 1 with 2 supplements
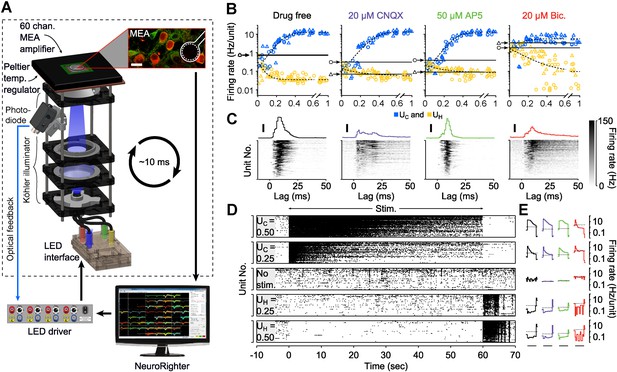
Optogenetic modulation of network activity in vitro.
(A) Multichannel recording, processing, and stimulation system. A 59-channel amplifier detects spiking activity produced by cells close to electrodes (white outline). Neurons express ChR2R-mCherry (red) and eNpHR3.0 under the CaMKllα promoter (green: immunoreactivity for CaMKllα; scalebar: 20 μm). Electrode voltages are processed in real-time and can be used to update an LED stimulator feeding a homogeneous Köhler illuminator below the MEA. An optical feedback circuit (blue line) ensures distortion free blue stimulus waveforms. (B) Time-averaged firing rates of two cultures (△ and ○) in response to 60-s applications of randomly valued UC and UH during different forms of synaptic blockade. Black horizontal bars indicate the cultures' spontaneous firing levels. Blue and yellow symbols indicate the mean firing level over a single trial at the corresponding value of UC and UH, respectively. The dotted lines are least-squares fits used to estimate the UC and UH saturation points provided in the text. (C) PSTH of individual units (grey scale) and the unit-averaged PTSH in response to 1 millisecond 5 mW mm−2 blue light pulses for each drug condition. Scale bars, 50 Hz/unit. (D) Raster plots for 87 detected units during 60-s applications of UC and UH. The firing rate evoked by stimulation using a particular value of UC and UH decays over the course of the protocol. (E) The trial-averaged firing rate profiles for the stimulus levels presented in (D) across drug conditions. Black horizontal lines indicate the 60 s stimulation period. Dotted lines indicate spontaneous firing levels. Note the log scale. In (C) and (E), line colors indicate the drug conditions above each panel in (B).
Figure 1—figure supplement 1
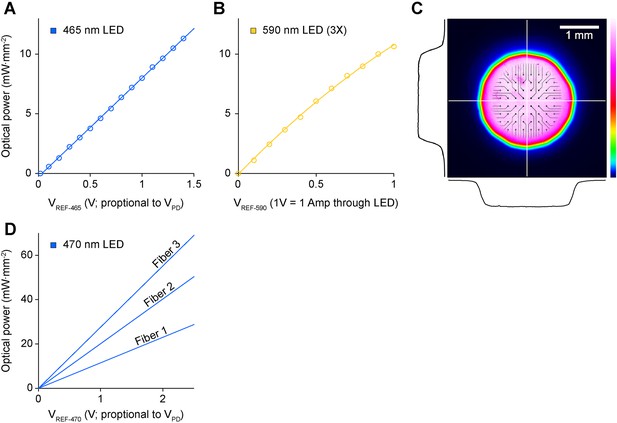
Optical characteristics of the in vitro stimulator and in vivo fiber.
(A, B) Optical power density at the culture as a function of the reference voltage sent to the LED driver from NeuroRighter's digital to analog converters for the in vitro stimulator. (A) For the blue (465 nm) LED, we used optical feedback to completely linearize the relationship between the reference voltage and optical power (Figure 1A in the main text; https://github.com/jonnew/cyclops; ‘Materials and methods’). This enabled the delivery of complex, distortion-free stimulus waveforms, such as sinusoidal and triangle waves (Figure 4). (B) For the yellow LEDs (590 nm) we used current regulation mode to control optical intensity. (C) Colormap indicating the uniform spatial light intensity profile projected onto the MEA surface using a Köhler illuminator (Figure 1A in the main text). The black lines show cross sectional intensity profiles through the horizontal and vertical center of the illuminated region (white lines). The MEA image is superimposed on the profile to provide an indication of scale. (D) Power density at the tip of the three 125 μm diameter fibers used for in vivo stimulation as a function of a reference voltage provided by the real-time controller. Differences in power across fibers are due to disparities in fiber coupling efficiency along with circuit tuning that was performed to ensure linearity over the reference voltage range prior to each experiment.
Figure 1—figure supplement 2
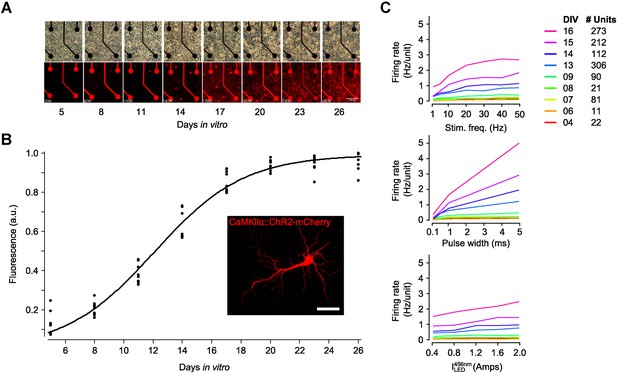
Expression time course of AAV2-CaMKIIα-ChR2(H134R)-mCherry.
(A) Phase-contrast and confocal imaging of a single region of interest (ROI), containing 4 microelectrodes, performed over the first 26 days in vitro (DIV). Cultures were transduced at 1 DIV. (B) To quantify the expression time course, three or four ROIs were imaged in three cultures over the first 26 DIV. For each ROI and DIV, the integrated intensity of 600–690 nm light through the emission filter was calculated and then normalized by the maximal integrated intensity over the 26 day imaging period (black dots). A sigmoid of the form was fit to the resulting data using nonlinear regression (r2 = 0.98; MATLAB curve-fit toolbox). The half maximal expression point occurred at ∼12 DIV. (C) The time-course of ChR2R function was measured by recording the evoked network spiking response in three networks over the first 16 DIV. Each experiment applied 140 trains of 30 s stimulation periods, each consisting of a random combination of pulse frequency (1, 5, 10, 20, 30, 40, and 50 Hz), pulse width (0.1, 0.5, 1.0, and 5.0 ms), and 465 nm LED intensity (0.2, 0.4, 0.6, 0.8, and 1.0 Amps; current regulation was used because these experiments were performed prior to the creation of the linear LED driver shown in Figure 1—figure supplement 1). Stimulus bouts were separated by 30 s and were applied in random order. Colored lines show the average neuronal firing rate, across all three networks, at a set value for particular stimulation parameters. For example, the average network firing rate, , for a stimulus frequency of 20 Hz is.
where indicates the average over time and units. The legend indicates the number of units used to produce each line for each DIV. The monotonicity of these functions across development (except for high stimulus frequencies) indicates the achievable evoked firing levels at different developmental points and the potential of each of the stimulus parameters to be effective control inputs.
Figure 2 with 6 supplements
PI optical feedback allows precise control of network firing levels over 1-min epochs.
(A) (Top) Network firing rate during different trials (colors). Target firing levels (black lines) ranged from 0 to 10 Hz and were applied in random order. (Bottom) Control signals, UC and UH, required during closed-loop control. For this network, the controller saturated while attempting to clamp network firing at 10 Hz/unit, resulting in a control failure (grey trace). (B) Time-averaged firing rates for seven different networks during PI control (left axis, colors). The dotted line is identity representing perfect closed-loop control. The spontaneous firing rates of each network are indicated by black arrows. The RMS error between the measured and target firing for each network is shown as a function of the target rate (right axis, black markers). A trial was considered successful if the RMS error between the target and achieved firing rate was less than 0.5 Hz/unit (red line). (C) Time- and culture-averaged successful control signals vs target firing rates. The shaded areas indicate the minimum and maximum value across networks. All temporal averages in this figure were taken over the final 30 s of the control epoch.
Figure 2—figure supplement 1
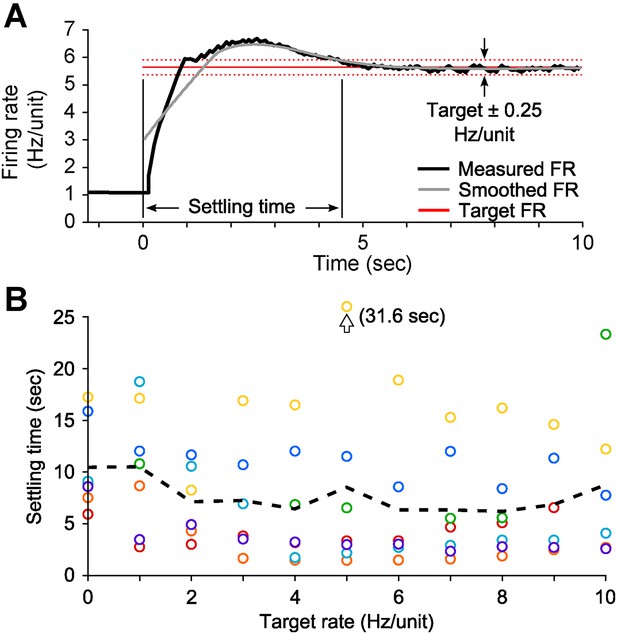
PI settling time in vitro.
(A) The settling time was defined as the time-point at which the smoothed firing rate (grey line; LOWESS with a 2.5 s smoothing window and a tri-cube weight function) entered and stayed within the boundaries defined by the target rate ± 0.25 Hz/unit (dotted red lines). (B) The settling time did not have a strong relationship with the target firing rate and was variable across cultures (mean ± SD: 7.8 ± 6.0 s, 7 cultures). Colors denote different cultures and the dotted black line indicates the mean across cultures for each target rate.
Figure 2—figure supplement 2
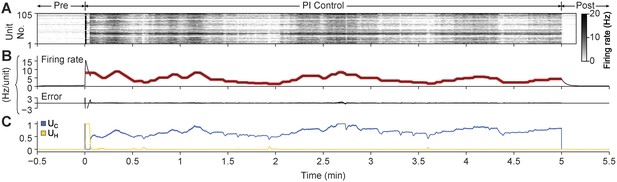
PI feedback permits control during a continuously changing target rate.
(A) Firing rate of detected units. Each row displays the firing rate of a particular unit, encoded by the grey-scale to the right (1 s bins). (B) The average firing rate of the network (black) and the target firing rate (red) and the error signal during different control periods. The target firing rate was moved up and down manually by the experimenter via mouse clicks on NeuroRighter's graphical interface for the duration of the 5-min control epoch. (C) Optical control signals delivered by the PI controller during the control epoch.
Figure 2—figure supplement 3
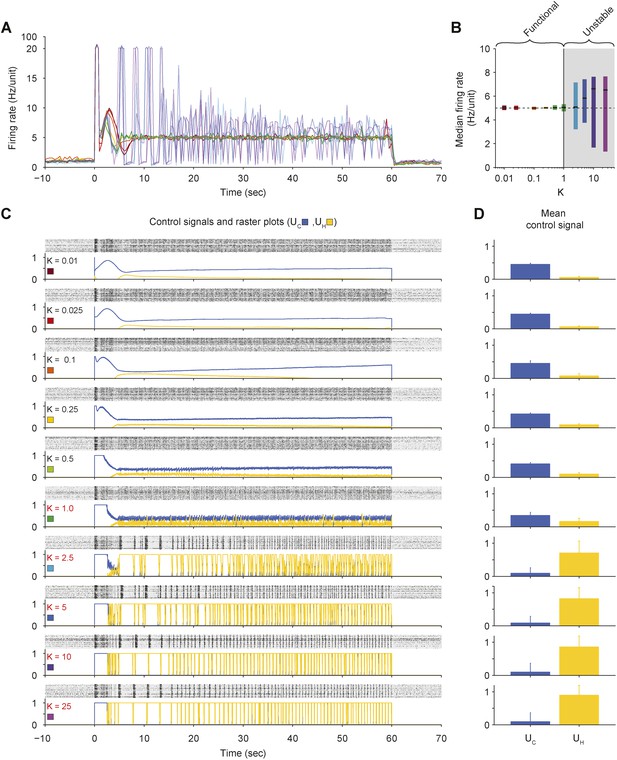
Effects of proportional gain (K) on closed-loop stability of PI control in vitro.
(A) The network firing rate is shown during control using different values of K (Ti = 1.0 s and τ = 2.5 s). Different values of K were used in random order and correspond to the colors shown in (C). Firing rates were calculated using a bin size of 1 s instead of the exponential moving average used by controller (Equation 1) to facilitate comparison with Figure 2—figure supplement 5 since the firing-rate filter time constant is manipulated in that experiment. (B) The median network firing rate (black lines) is shown with the interquartile range (colored bars) taken over each firing rate time series. Values of K greater than ∼1 cause the controller to become unstable, leading to large firing rate variance. (C) Firing rasters for individual units along with corresponding control signals for all values of K tested. Ineffective values of K are printed in red. (D) Mean control signals ± standard deviation over time.
Figure 2—figure supplement 4
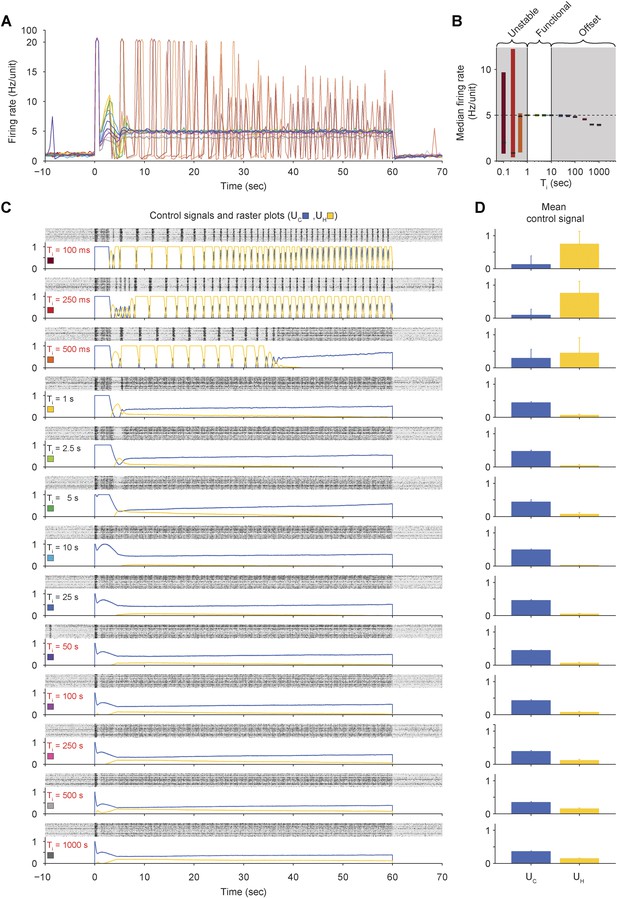
Effects of integral time-constant (Ti) on closed-loop stability and accuracy of PI control in vitro.
(A) The network firing rate is shown during control using different values of Ti (K = 0.1 and τ = 2.5 s). Different values of Ti were used in random order and correspond to the colors shown in (C). Firing rates were calculated using a bin size of 1 s instead of the exponential moving average used by controller (Equation 1) to facilitate comparison with Figure 2—figure supplement 5 since the firing-rate filter time constant is manipulated in that experiment. (B) The median network firing rate (black lines) is shown with the interquartile range (colored bars) taken over each firing rate time series. Values of Ti less than ∼1 s caused the controller to become unstable, leading to large firing rate variance. Values of Ti greater than ∼25 s introduced an offset. (C) Firing rasters for individual units along with corresponding control signals for all values of Ti tested. Non-functional values of Ti are printed in red. (D) Mean control signals ± standard deviation over time.
Figure 2—figure supplement 5
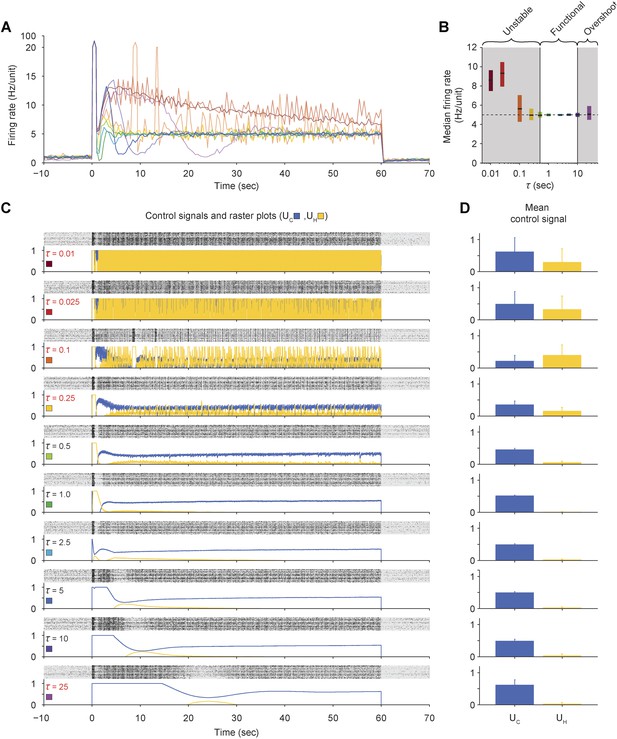
Effects of the firing-rate estimation time-constant (τ) on closed-loop stability of PI control in vitro.
(A) The network firing rate is shown during control using different values of τ (K = 0.1 and Ti = 1.0 s). Different values of τ were used in random order and correspond to the colors shown in (C). Firing rates were calculated using a bin size of 1 s so that different firing rate time-constants could be compared using a common time-scale. (B) The median network firing rate (black lines) is shown with the interquartile range (colored bars) taken over each firing rate time series. Values of τ less than ∼0.5 s caused the controller to become unstable, leading to large firing rate variance. Values of Ti greater than ∼10 s introduced large, slow oscillations that caused significant target overshoot. (C) Firing rasters for individual units along with corresponding control signals for all values of τ tested. Non-functional values of τ are printed in red. (D) Mean control signals ± standard deviation over time.
Figure 2—figure supplement 6
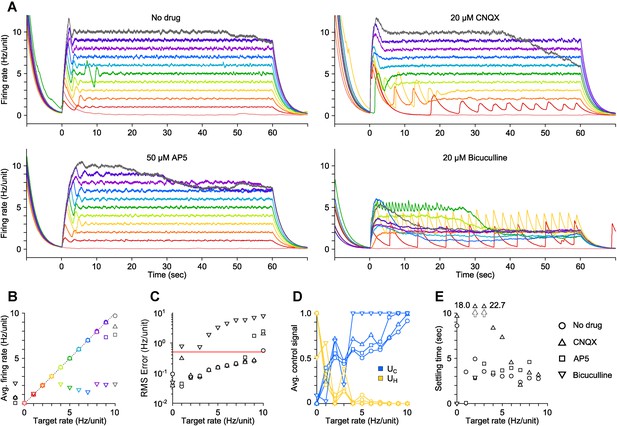
PI control of firing levels during synaptic blockade in vitro.
(A) Network firing rate for different trials (colors) in the presence of various competitive neurotransmitter receptor antagonists (○ no drug, △20 μM CNQX, □50 μM AP5, ▽20 μM bicuculline). Trials were presented in a random sequence that was repeated across drug conditions. (B) Time-averaged network firing rates during PI control, for each drug tested. Spontaneous firing rates of the network during each pharmacological condition are represented by black symbols to the left of the ordinate axis. The dotted line represents perfect clamping of mean activity to the target rate. (C) RMS tracking error between the measured and target firing for each pharmacological condition as a function of the target rate. Control failure occurred for each point above the red line, which was defined as RMS tracking error > 0.5 Hz/unit. CNQX, which blocks AMPARs, destabilized the network somewhat, likely though the removal of recurrent inhibition, and resulted in a control failure for the 2 Hz/unit target. AP5, which blocks NMDARs, reduced the dynamic range of evoked activity and slowed the rise-time of the population response (compare to control onset in (A)). Bicuculline, which blocks GABAARs, strongly destabilized network activity and resulted in control failure for all but two target rates: 0 and 2 Hz/unit. In the presence of bicuculline, average network firing levels could not be pushed higher than ∼2 Hz/unit. Interestingly, the only successful non-zero target rate was the one closest to the spontaneous network firing rate in the presence of bicuculline. (D) Time-averaged control signals and (E) settling times (Figure 2—figure supplement 1) vs target rate for each pharmacological condition. All data in this figure are from a single culture. All temporal averages in this figure were taken over the final 30 s of the control epoch.
Figure 3
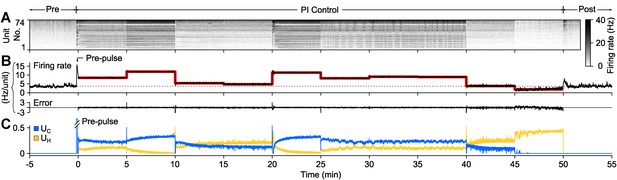
PI feedback control to track a changing target rate.
(A) Firing rate of detected units. Each row displays the firing rate of a particular unit, encoded by the grey-scale to the right (1 s bins). (B) The average firing rate of the network (black), the target firing rate (red), and the error signal during different control periods. The pre-control firing rate is indicated by a dotted line. (C) Optical control signals delivered by the PI controller during the control epoch.
Figure 4
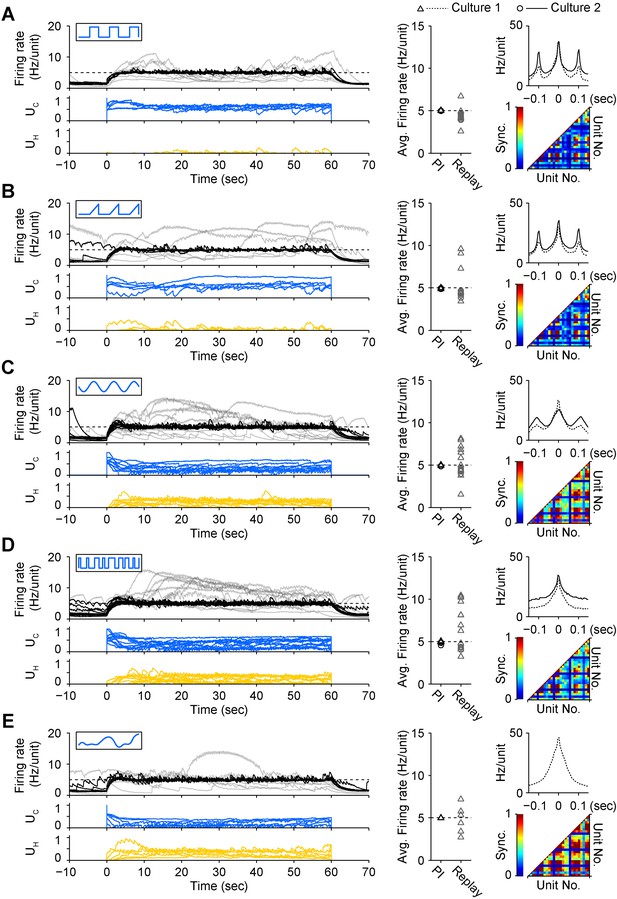
A diverse set of optical input signals can be used to clamp network firing rate, and accurate firing rate control requires closed-loop stimulation.
(A) Left, network firing rates during closed-loop control (black) and during replay of closed-loop control signals in open-loop (grey), along with corresponding control inputs UC (blue) and UH (yellow). These time series data were derived from culture 1. Note that in all instances, open-loop replay of input signals recorded from previous successful closed-loop control failed to clamp firing levels and resulted in erratic activity levels over the control epoch. Middle, time-averaged firing rates for both cultures during closed-loop control (black) and during subsequent replay of control signals in open-loop (grey). Right, average unit-to-unit cross-correlogram for both cultures (top, bin = 5 ms) and unit-to-unit synchronization structure for culture 1 (bottom) during optogenetic feedback control. Synchronization was defined as,
where Ncc is number of correlated events within ± 10 ms, and Ni and Nj are the number of spikes from units i and j used to calculated the cross-correlogram.
(B) Same as (A) for triangle optical stimuli modulated according to.
(C) Same as (A) for sinusoidal optical stimuli modulated according to.
(D) Same as (A) for pseudo-random binary sequence of optical pulses modulated according to.
(E) Same as (A) for continuous optical stimuli modulated according to.
Each protocol was performed in the same culture.
Periodic stimuli (panels A–C) were applied at 10 Hz so that the periodicity of evoked activity would be apparent in the correlation functions. In all cases, the 590 nm light was modulated according the standard control scheme (Equation 10 of ‘Materials and methods’). Note that each input type evokes a unique correlation and synchronization structure while still achieving accurate firing rate control.
Figure 5 with 2 supplements
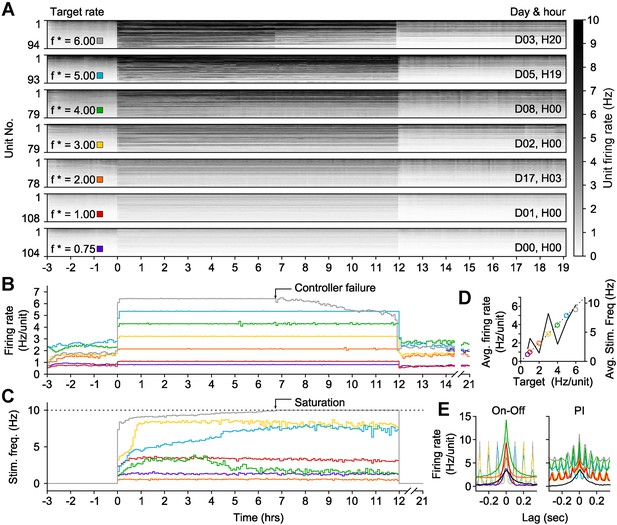
On-off feedback control of population firing rate over 12-hr epochs.
(All data presented in this figure were obtained from a single culture over the course of ∼3 weeks.) (A) Firing rates of detected units during 12-hr control periods are represented using the grey-scale to the right. At time 0, the on-off controller was engaged and the average network rate was clamped firing to the target rate indicated to the left of each chart. The day and hour of each protocol, relative to the first experiment, is shown to the right. Units are sorted by their mean firing rate during the 3-hr period prior to closed-loop control. (B) The network firing rate during each control epoch (5-min bins). The color map corresponds to the target rates shown in (A). (C) Closed-loop stimulation frequency over the course of the 12-hr clamp. For a target rate of 6 Hz/unit, the controller saturated at the maximal frequency of 10 Hz at around 7 hr into the control epoch, and target tracking failed as a result. (D) Time- and unit-averaged firing rates (colors, left axis) and control signal (black, right axis) across each 12-hr clamping period. The dotted line is identity. (E) The average cross-correlation function between 30 randomly selected units during on-off or PI control are plotted for each target rate. The correlation function for spontaneous activity is shown in black. When low stimulation frequencies were required, the unimodal correlation structure of spontaneous activity was preserved using on-off control.
Figure 5—figure supplement 1
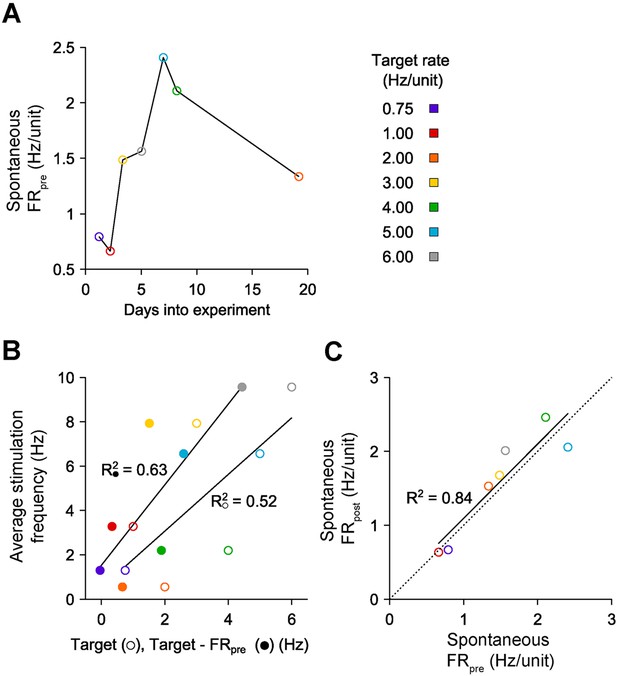
Characteristics of on-off control over weeks in vitro.
(A) Spontaneous, pre-stimulation firing rates over the course of 7 long-term excitatory on-off control experiments with a single culture. Spontaneous excitability changes smoothly across the ∼20 days during which 12-hr firing rate control experiments were conducted. (B) The average stimulation frequency required to achieve firing rate control is plotted against the target rate (○) and the difference between the target rate the pre-stimulation spontaneous firing level (●). A linear fit is improved when the spontaneous excitability is taken into account, indicating that ongoing changes in network excitability influence the intensity of stimulation required to achieve firing rate control. (C) The spontaneous firing rate before each 12-hr protocol vs the spontaneous firing rate following each protocol exhibits a strong linear relationship (black line) that is not significantly different from identity (dashed line). This indicates the absence of a homeostatic decrease in network activity that might have resulted from chronically elevated firing levels in the absence of pharmacological agents.
Figure 5—figure supplement 2
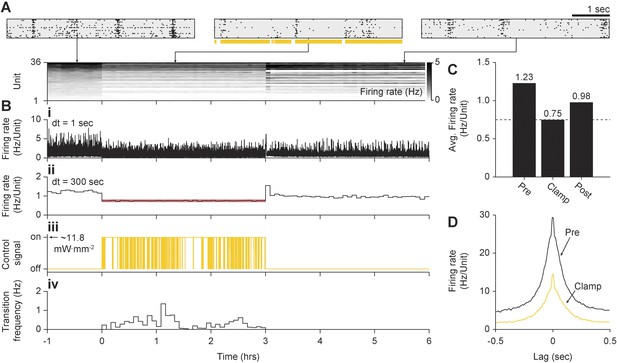
In vitro inhibitory on-off control using Arch3.0.
(A) Summary of unit spiking activity. (Top) Rastergrams show zoomed portions of spiking activity taken from the pre-clamp, clamp, and post-clamp periods of the experiment. Arrows indicate the time during the experiment that each reastergram was derived from. (Bottom) Firing rate histogram for the duration of the 7-hr recording for each unit, using 5-min bins. Firing levels are indicated by the grey-scale to the right. (B) Summary of network firing rates and the corresponding control signal. (B.i) Network firing rate calculated using 1 s bins and (B.ii) 5-min bins. The red line indicates the 0.75 Hz/unit target rate. (B.iii) Raw on-off control waveform. (B.iv) On-to-off transition frequency histogram calculated using 5-min bins. (C) Time-averaged firing rates for each epoch of the experiment with numerical values written above the bars. Note that post-clamp firing levels did not show a homeostatic increase due to 3-hr of firing rate suppression. (D) Average unit-to-unit spike correlogram during the pre-clamp and clamp period. Note that the correlation time and structure were very similar in both conditions. The correlogram derived from the clamp period appears to be a scaled version of the pre-clamp correlogram due to decreased firing levels.
Figure 6
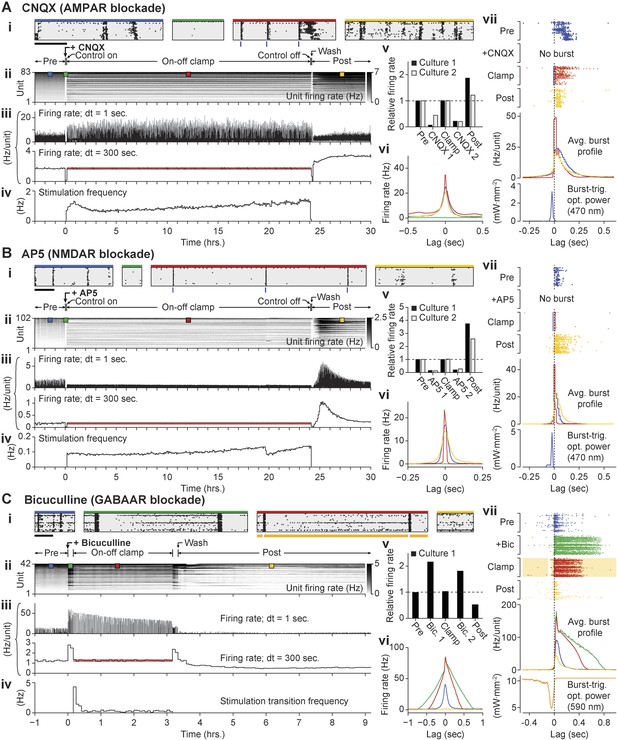
Decoupling spiking and neurotransmission using on-off feedback control.
(A) Summary of a 24-hr AMPAergic neuortransmission/spiking decoupling protocol. (A.i) Rastergrams show zoomed portions of spiking activity taken from discrete times during the experiment. Top color bars indicates recording epoch. Blue bars beneath indicate stimulus times. Horizontal scale bar, 1 s (A.ii) Firing rate histogram for the duration of the 33-hr recording for each unit, using 5-min bins. Firing levels are indicated by the grey-scale to the right. CNQX (AMPAergic receptor antagonist) was added at time 0 and removed 24 hr and 10 min later. Closed-loop stimulation began 5 min after CNQX addition and lasted 24 hr. Colored boxes indicate the location of the data used in the zoomed rastergrams, crosscorrelograms, and burst profiles. (A.iii) The average unit firing rate using 1-s bins and 5-min bins. The red line indicates the target rate. (A.iv) Closed-loop stimulation frequency. (A.v) Time- and unit-averaged firing rates for each epoch, normalized to the pre-drug firing level. The ‘post’ firing rate was evaluated over 6 hr following the drug wash. (A.vi) The average unit to unit crosscorrelogram for each control epoch. (A.vii) Example burst ratergrams, average burst profiles, and burst-triggered stimulus optical intensity for each control epoch. The location of the data used to calculate (A.vi) and (A.vii) is indicated by the matching colored boxes in (A.ii). (B, C) Same as (A) but using AP5 (B) or bicuculline (C) to block NMDAergic and GABAergic neurotransmission, respectively. For bicuculline, the firing rate was clamped over a 3 hr period. The changes in spontaneous firing levels before on-off control for each culture were: CNQX, −93.8 and −56.3%; AP5, −87.3 and −84.5%; bicuculline, +116.2%, and upon relief from on-off control: CNQX, −78.7 and −80.0%; AP5, −73.0 and −80.4%; bicuculline: +81.3%.
Figure 7 with 3 supplements
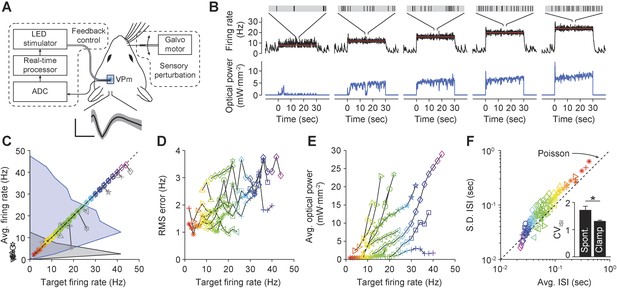
Firing rate control of isolated thalamic units, in vivo.
(A) Single unit extracellular recordings were performed in thalamic VPm and used to update the optical power of the LED stimulator. The primary vibrissa could be deflected along the rostral–caudal plane using a galvanometer-based scanning motor to provide sensory perturbations during closed-loop control. A representative TCU waveform is shown (black line is the mean and the shaded region is ± 1 SD). Vertical and horizontal scale bars represent 100 μV and 1 ms, respectively. (B) Single-trial closed-loop firing rate control in the absence of sensory input. Traces show the target firing rate (red), measured firing rate (black), and light power (blue). Inset spike trains display 1 s of activity for each target rate. (C) Time-averaged firing rates vs target rates for 10 TCUs (symbols). Data points are color coded according to the target rate. Black symbols at left indicate spontaneous firing levels prior of closed-loop control. Grey symbols indicate control failure. Data points derived from a single TCU are connected with a line. Shaded areas are peak-normalized histograms of spontaneous firing rates (black) and successfully controlled firing rates (blue) across units. (D) RMS tracking error for each target rate. (E) Average light power required for each target rate. (F) Mean vs standard deviation of the ISI distribution for each target rate. The dotted identity line indicates Poisson firing statistics. Inset bar chart shows the mean CVISI across units during spontaneous and clamped firing. *p = 0.043; t-test.
Figure 7—figure supplement 1
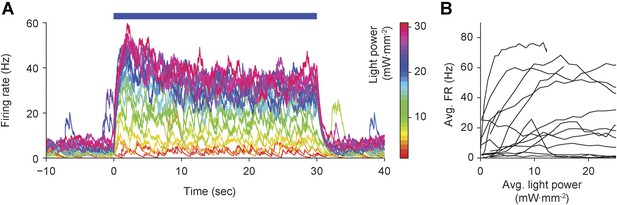
Open-loop application of precisely defined optical stimuli results in highly variable, non-stationary evoked firing levels in the intact rat vibrissa system.
(A) Continuous, 30-s optical stimuli (blue bar) of linearly increasing intensity across trials (scale bar at right) were applied to 13 TCUs. Although evoked firing, as measured by the optrode in VPm thalamus, tended to increase monontonically with light power (as indicated by the preservation of color ordering in the time-series overlay), evoked firing was non-stationary and highly variable during each 30-s stimulation epoch. (B) Time-averaged evoked firing rates were highly variable for a given light intensity across TCUs, reflecting differences in channel expression, depth of anesthesia, and other uncontrolled variables affecting neuronal excitability.
Figure 7—figure supplement 2
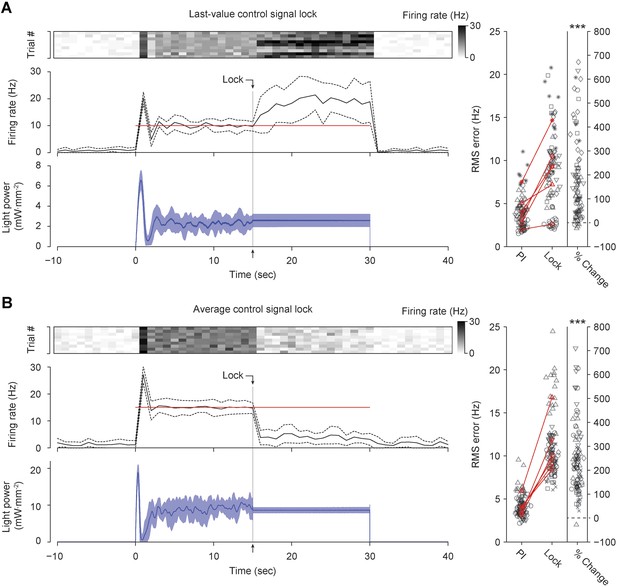
Continuous real-time update of optical intensity is required for accurate firing rate control in the intact rat vibrissa system.
(A) 15 s into each 30-s control epoch, the control signal (blue) was locked at its most recent value. (Top) The firing rate of a single TCU, encoded by the scalebar at right, is shown for 10 control trials (columns). (Middle) The trial-averaged firing rate (black) line, and target rate (red line). Dotted lines indicate ± standard deviation. Bin size, 1 s (Bottom) Trial-averaged optical control signal. Shading indicates ± standard deviation. (Right) The RMS tracking error during functional integral control and during the locking period are shown for 6 TCUs (symbols). Black symbols represent individual trials and red symbols are trial-averages. Red lines connect means derived from the same unit. The rightmost column indicates the percent change in RMS tracking error during the control lock compared to the functioning integral control for each trial. The mean RMS error increased 204 ± 227% during the locking period compared to integral control (*** p = 1.07 × 10−15, Wilcoxon signed-rank test). (B) Same as (A) except that the control signal was locked at the average value taken during the first 15 s of control. The mean RMS tracking error increased 240 ± 145% during the locking period compared to integral control (*** p = 1.25 × 10−17, Wilcoxon signed–rank test).
Figure 7—figure supplement 3
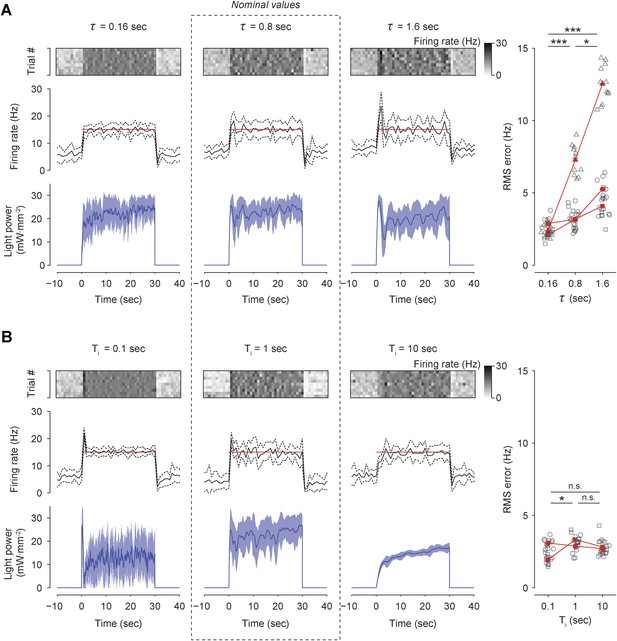
Effects of firing-rate filter time-constant (τ) and integral time-constant (Ti) on performance of integral control in vivo.
(A) The firing rate was controlled in three TCUs using 3 different values of τ: 0.16 s, 0.8 s (nominal), and 1.6 s (Top) The firing rate of a single unit, encoded by the scalebar at right, is shown for 10 optoclamp trials (rows). (Middle) The trial-averaged firing rate (black) line, and target rate (red line). Dotted lines indicate ± standard deviation. Bin size, 1 s (Bottom) Trial-averaged optical control signal. Shading indicates ± standard deviation. (Right) The RMS tracking error during integral control for each value of τ is shown for each unit (symbols). Black symbols represent individual trials and red symbols are trial-averages. Red lines connect means derived from the same unit. *p = 0.010, **p = 1.4 × 10−6, and ***p = 1.2 × 10−10. (B) Same as (A) except that firing rate was controlled in two TCUs using 3 different values of Ti: 0.1 s, 1.0 s (nominal), and 10 s. *p = 0.019. For both (A) and (B), a Kruskal–Wallis one-way analysis of variance was followed by post-hoc Mann–Whitney U tests, using a Bonferroni correction to control the familywise error rate. Adjusted p values are reported.
Figure 8 with 1 supplement
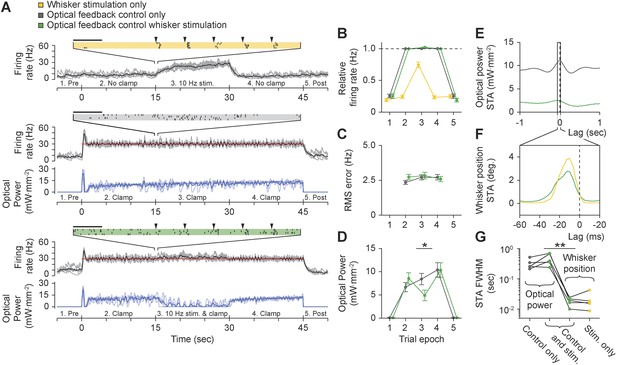
Using optogenetic feedback to control thalamic activity state during ongoing sensory input.
(A) Real-time control of thalamic firing levels during external sensory drive. The firing rate of a single TCU cell (grey lines: single trials; black lines, average) is shown for three interleaved protocol types: 15-s trains of whisker stimuli (yellow), 45-s closed-loop control periods in the absence of whisker input (grey), and closed-loop control during concurrent whisker stimulation (green). (Top) 10 Hz whisker deflections occurred from 15–30 s within each trial (black triangles). Inset raster plot shows spikes times for 4 trials at the onset of whisker stimulation. (Middle) TCU firing was clamped at 30 Hz (red line) for the duration of each trial. Blue lines show the optical control signal (light blue: single trials; dark blue: average). (Bottom) TCU firing was clamped at 30 Hz (red line) for the duration of each trial and whisker stimuli were delivered from 15–30 s within each trial. Horizontal scale bars on the firing rasters indicate 100 ms. (B) mean relative (measured/target) firing rates, (C) mean RMS tracking errors, and (D) mean optical power across trials and units. Values are shown for each of the 5 trial epochs indicated on the abscissa axis of each time series in (A). Error bars indicate ± SEM. (E) Spike-triggered average (STA) optical power and (F) STA whisker position for the TCU shown in (A). Note the difference in time scales between (E) and (F). (G) FWHM of the STA for each TCU across trial types. Sample sizes: 5 TCUs, 3 to 5 applications of each protocol type per unit. *p = 0.024, **p = 0.0079; Mann–Whitney U Test.
Figure 8—figure supplement 1
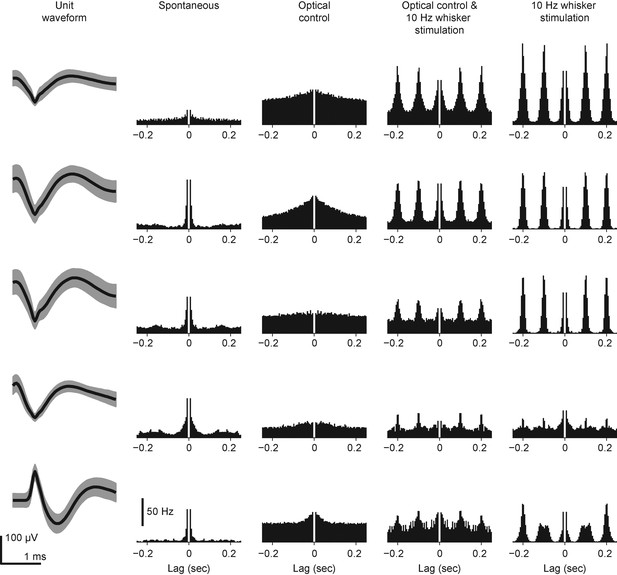
Spike waveforms and autocorrelograms of TCUs used for concurrent optogenetic feedback control and whisker stimulation in intact rats.
Shown for each of the 5 TCUs are the spike waveform and autocorrelogram of spiking activity during different portions of the control epoch. For the spike waveform, the thick black line represents the mean and shading is ± 1 standard deviation. The bin size used to calculate the autocorrelogram was 5 ms. The autocorrelogram histogram was normalized by the bin size and number of spikes to arrive at a firing rate.
Figure 9
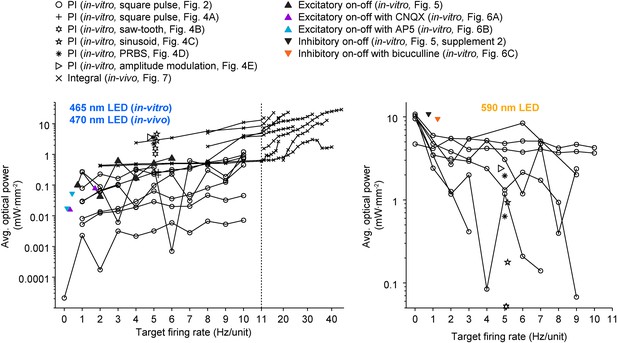
A wide range of optical power was required during successful closed-loop control in vitro and in vivo.
The time-averaged power density of blue (left plot) and yellow (right plot) light vs the corresponding target firing rate is shown for all control algorithms and experimental preparations used in the paper. Lines connect data points derived from the same culture (in-vitro data) or unit (in-vivo data; note the log scales). Only successful control trials are shown. The light intensity required during closed-loop control varied across orders of magnitude and depended on the target rate, control algorithm, stimulus waveform, type of neural preparation being controlled, and variability in cell-to-cell and culture-to-culture excitability. This highlights the ability of closed-loop control to compensate for the experimental variability across preparations, equipment, and algorithms, as well as the intrinsic variability in neural circuits, to achieve a target activity level.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Optogenetic feedback control of neural activity
eLife 4:e07192.
https://doi.org/10.7554/eLife.07192
