Rate and timing of cortical responses driven by separate sensory channels
- University of Chicago, United States
- Vanderbilt University Medical Center, United States
Figures
Figure 1 with 2 supplements
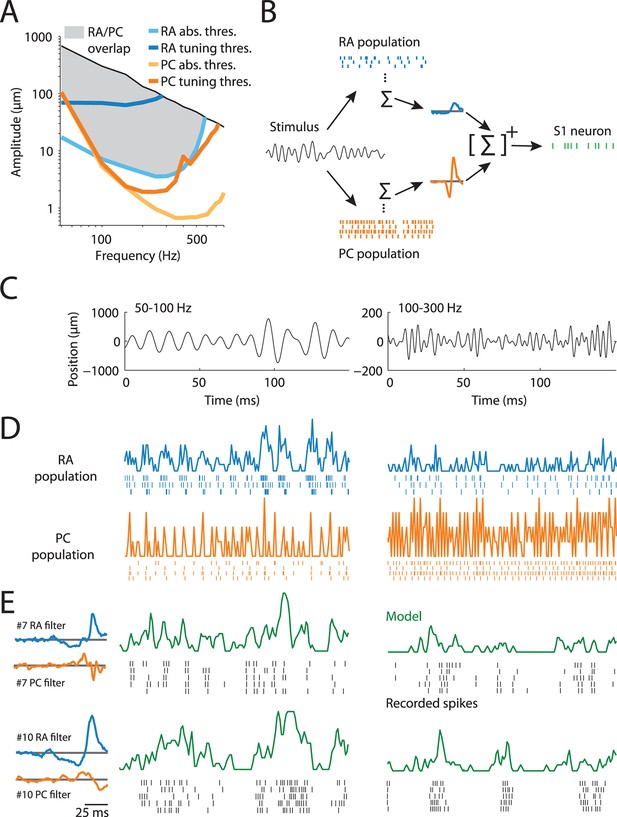
Characterizing the transformation between peripheral and cortical responses.
(A) Frequency–amplitude pairs that elicit responses in rapidly adapting (RA) and Pacinian (PC) afferents. Light blue and orange lines indicate absolute response thresholds for RA and PC afferents (as determined by the peripheral model), respectively, while the dark blue and orange lines denote tuning thresholds (i.e., eliciting one spike on each stimulus cycle). The black line corresponds to the highest amplitude the stimulator could deliver at a given frequency and likely exceeds the maximum amplitude that one is liable to encounter during every day tactile experience. While RA and PC afferents are maximally sensitive at different frequencies, most frequency–amplitude pairs elicit responses from both afferent classes (indicated by the shaded region). (B) Illustration of the model that describes the transformation from peripheral to cortical responses. A broadband noise stimulus activates both RA and PC afferents. RA and PC population responses are each convolved with a temporal filter, then summed and rectified to culminate in the responses of individual S1 neurons. (C) Two examples of vibratory stimuli. (D) Simulated RA (blue) and PC (orange) population firing rates along with spike trains of a subset of neurons in the population. See Figure 1—figure supplement 1 for details on how the peripheral population models were validated. (E) Recorded spikes (black ticks) over five stimulus repeats and model predictions (green traces) for two cortical neurons, whose RA and PC filters (plotting filter magnitude over time) are shown on the left. Cortical neurons differ in their response properties, such as burstiness and temporal precision, and the model captures these broad differences with different RA and PC filters. See Figure 1—figure supplement 2 for assessment of the general predictive power of our model.
Figure 1—figure supplement 1
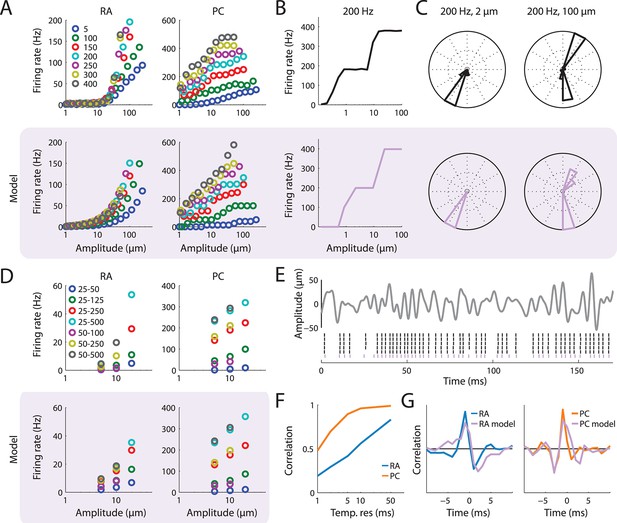
Simulation of populations of RA and PC afferents.
(A) Recorded (top) and simulated (bottom) responses of RA and PC populations to sinusoidal skin vibrations of different amplitude and frequency. The model predictions closely approximate measured firing rates. (B) Rate-intensity function for a recorded (top) and simulated (bottom) PC afferent stimulated with 200 Hz sinusoidal vibrations. Both the recorded and modeled PC afferent exhibit entrainment plateaus. (C) Cycle histograms for a recorded (top) and a simulated (bottom) PC afferent. At low amplitudes, a single spike is elicited per cycle, which is precisely timed to occur at the same phase within the cycle (left column). At higher amplitudes, more than one spike per cycle can occur in complex but repeatable patterns (right column) (Whitsel et al., 2000). Both of these effects are captured by the model. (D) Mean rate-intensity functions for recorded (top) and simulated (bottom) populations of RA and PC fibers stimulated with bandpass noise skin vibrations of different amplitudes and frequency composition (legend denotes frequency ranges in Hz). The model predictions closely approximate recorded firing rates. (E) Reproducing precise spike timing for bandpass noise stimuli. Top: Example of a noise trace. Bottom: Recorded (black) and simulated (lavender) response a single PC fiber to stimulus. The simulated spike train matches the recorded ones with high temporal precision. (F) Correlation between recorded and simulated RA (blue) and PC (orange) population response for noise stimuli at different temporal resolutions. The lower correlation for the RA responses at the finest temporal resolution reflects the fact that RA responses are not very repeatable at those timescales (Mackevicius et al., 2012). (G) Mean spike triggered averages (STA) for RA (left) and PC (right) fibers calculated from both the recorded (blue and orange) and modeled (lavender) data with respect to the stimulus trace. The STA for the model and the recorded peripheral data agree well.
Figure 1—figure supplement 2
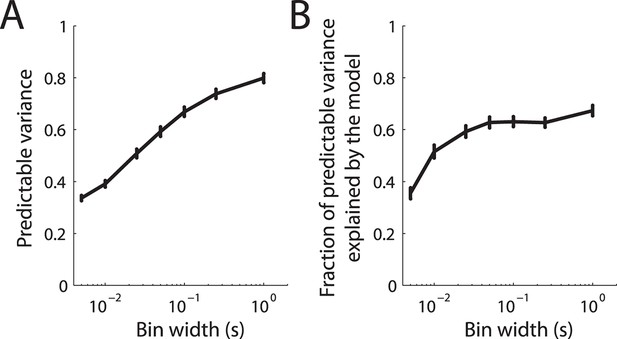
Prediction accuracy of fitted LNP model.
(A) Predictable variance in the recorded cortical spike trains as a function of bin width. The solid line denotes the mean over the cortical population and the error bars denote the standard error of the mean. Due to jitter in the recorded spike trains, the predictable variance decreases for finer bin sizes. (B) Fraction of predictable variance explained by the model as a function of bin width. The solid line denotes the mean over the cortical population and the error bars denote the standard error of the mean.
Figure 2 with 1 supplement
Rapidly adapting (RA) and Pacinian (PC) input is integrated differently.
(A) Fraction of neurons in areas 3b and 1 that receive input from both RA and PC populations (grey bar) or from only the RA population (blue) as assessed by whether input from the respective class is weighted more highly than might be expected by chance. Most S1 neurons receive input from both RA and PC afferents. (B) Mean RA and PC filters (solid lines) and the 5th and 95th percentile of filter values across all S1 neurons indicated by the light-shaded regions. RA and PC filters are systematically different. (C) Ratios of RA and PC filter magnitudes for neurons integrating information from both afferent classes. RA input tends to be weighted more strongly. (D) Width of RA and PC filters. RA input tends to be integrated over longer timescales than does PC input. Insets show example filters that are close to the population average (over 100 ms). (E) Excitation indices for all RA and PC filters, where 1 denotes purely excitatory input, 0 balanced input, and -1 purely suppressive input. RA filters almost always lead to a net positive excitation of the cortical neurons, while the PC filters are more diverse, on average balanced, and often suppress cortical response. Insets show example filters that are close to the population average (over 100 ms). See Figure 2—figure supplement 1 for validation of the analysis.
Figure 2—figure supplement 1
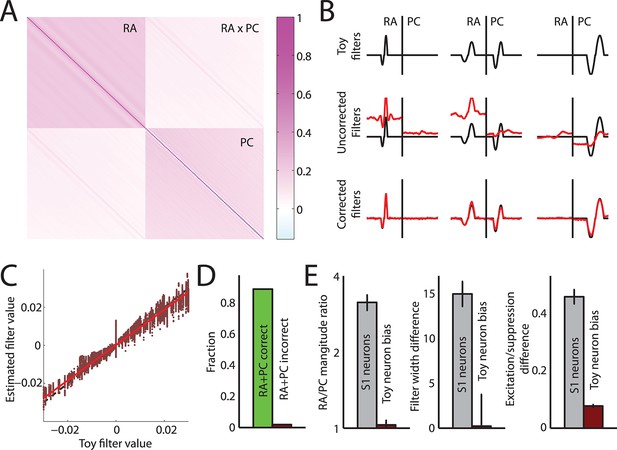
Accuracy of linear filter estimation.
(A) Autocorrelation matrix of RA and PC population responses from our data set to bandpass noise stimuli. (B) Examples of estimated linear filters from simulated neuronal responses. Top row: Three different filter sets. Middle row: Recovered filters assuming RA/PC populations responses are uncorrelated, leading to biases in the estimated filters. Bottom row: Recovered filters after correcting for autocorrelations in the RA/PC population input. The corrected filters closely match the actual filters. (C) Estimated filter value versus actual filter value across all filters and time points obtained from simulated neuronal responses. Estimated values closely match the actual values. (D) Fraction of simulated neurons correctly classified as having both RA and PC input (green bar) or incorrectly classified as having both RA and PC input when they had only input from one population (red bar). Neurons are classified correctly in the vast majority of cases; importantly in only 3% of cases were neurons misclassified as having both RA and PC input when in fact they only received input from one of the two. (E) Comparison of differences reported between RA and PC filters (grey bars) as reported in the main text (cf. Figure 2) and biases when calculating the same metrics from the simulated neuronal responses (red bars). In all cases, any biases are much smaller than the reported effects and are therefore unlikely to affect the results reported in Figure 2.
Figure 3
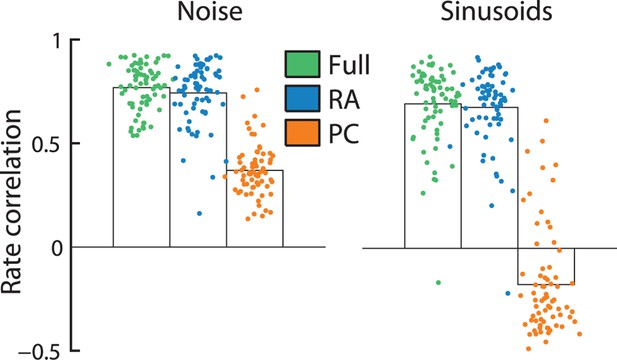
Rapidly adapting (RA) input determines cortical firing rates.
Reconstruction accuracy of the full model compared to one that includes only RA or Pacinian (PC) input as measured by correlation between actual and predicted firing rates (measured over the duration of the trial, namely 1 s). Error bars denote the standard error of the mean across neurons. Firing rates elicited by both noise and sinusoidal stimuli are well predicted by the full model. While the performance of RA-only filters is almost as good as the full model, reconstruction accuracy drops dramatically if only PC input is included.
Figure 4 with 1 supplement
Precise spike timing of S1 neurons is driven by Pacinian (PC) input.
(A) Responses to noise stimuli from two example neurons with particularly precise responses. Spiking probabilities derived from the full model (green traces) are much more temporally precise than are those derived from a rapidly adapting (RA)-only model (blue traces), reflecting the importance of PC input in shaping the response at fine timescales. Five repetitions of the recorded cortical spike trains are shown below the model traces in black. (B) Fraction of the explained variance (R2) by either the RA (blue) or PC (orange) model relative to the full model across different temporal resolutions for the two neurons shown in A. PC input is important to explain responses on fine timescales. (C) Fraction of explained variance (R2 fraction) relative to the full model by RA and PC input for all neurons at two different temporal resolutions. While RA input can explain most of the observed variance at coarse temporal resolutions (left panel), PC input is needed to explain the timing of cortical responses at fine temporal resolutions (right panel). See Figure 4—figure supplement 1 for further analysis. (D) Vector strengths predicted by RA (blue) and PC (orange) models relative to their measured counterparts at different frequencies across all neurons. RA input accounts for entrainment to sinusoidal stimuli at low frequencies, while PC input is needed at higher frequencies.
Figure 4—figure supplement 1
Fraction of variance explained as a function of timing precision of cortical neurons.
Fraction of variance explained by the RA-only model as a function of neural timing precision (as assessed by the highest frequency, the neurons reliably phase-locked) for two different bin sizes. At coarse temporal resolution, RA input explains almost all variance explained by the model independent of whether the neuron's spiking was precise or not. At fine temporal resolutions, RA input alone cannot explain the model's performance. The more precise a neuron's response, the less RA input alone could account for its response, indicating that the PC input accounts for more precise cortical responses.
Figure 5
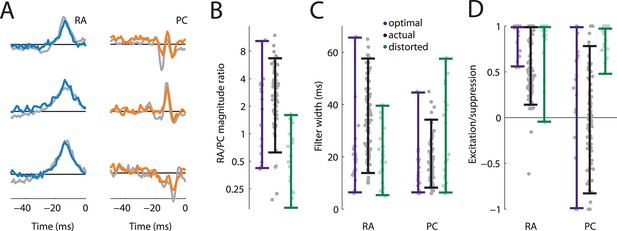
Rapidly adapting (RA) and Pacinian (PC) input is integrated optimally.
(A) Three examples RA and PC filters, each optimized for a different natural texture (colored traces) and paired with a filter from a cortical neuron that most closely matches it (gray traces). (B–D) Comparison of filter statistics for actual (black) and optimized (lavender), and distorted (green) filters for the RA/PC magnitude ratio (B), filter width (C), and excitation/suppression index (D). For the optimized filters, bars denote the range covered by the filters optimized for different textures. For the actual filters, bars indicate the range between the 10th and the 90th percentile.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Rate and timing of cortical responses driven by separate sensory channels
eLife 4:e10450.
https://doi.org/10.7554/eLife.10450
