Simple biophysics underpins collective conformations of the intrinsically disordered proteins of the Nuclear Pore Complex
- University of Toronto, Canada
- University of Pittsburgh, United States
- University of Basel, Switzerland
- Institute for Biomaterials and Biomedical Engineering, University of Toronto, Canada
Figures
Figure 1
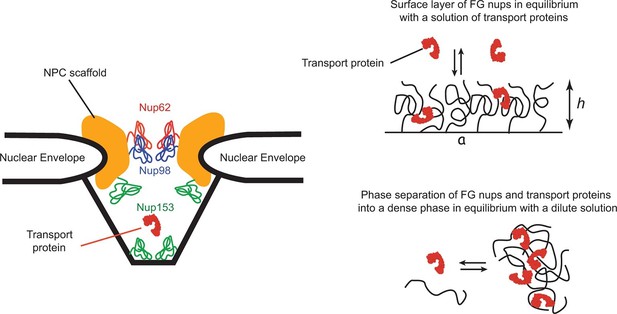
Schematic illustration of spatial arrangements of the FG nups in the NPC and in vitro models.
Left: schematic rendering of the NPC geometry (not to exact scale). The vertebrate FG nucleoporins discussed in this paper (Nup62, Nup98 and Nup153) and their approximate locations within the NPC are highlighted in color (Chatel et al., 2012; Krull et al., 2004; Chug et al., 2015). Other FG nups are not shown. Yeast NPC has an overall similar architecture but smaller dimensions. Vertebrate FG nucleoporins discussed in the paper have yeast analogues: Nsp1 is analogous to Nup62, while Nup100 and Nup116 are analogous to Nup98 in their sequence and the biophysical and functional properties. Right upper panel: schematic depiction of one typical in vitro experimental setup of a grafted FG nup layer in equilibrium with a solution of transport proteins. Right lower panel: some FG nups, such as Nup98, phase separate at high concentration and form a dense phase in equilibrium with a dilute solution.
Figure 2 with 1 supplement
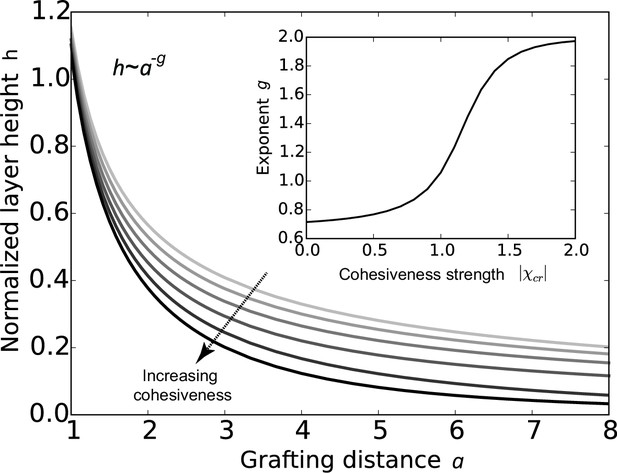
Cohesion makes FG nup layers more compact: theoretical predictions.
Layer height normalized by the chain length as a function of the normalized grafting distance for increasing cohesiveness ( varies from to ). For any value of , the curve is well approximated by the dependence . The inset shows that the exponent increases from to as the absolute value of the cohesion strength .
Figure 2—figure supplement 1
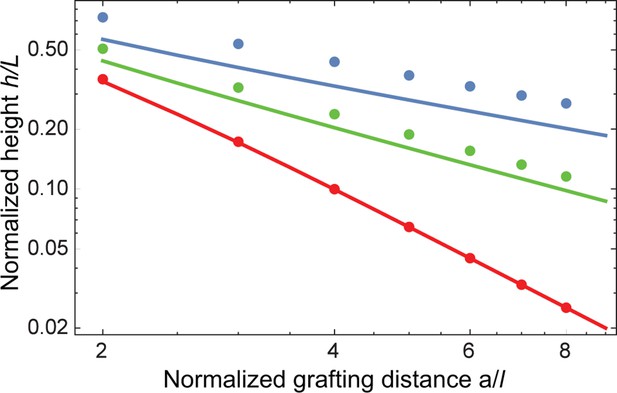
Effect of density non-uniformity on the model predictions.
The continuous lines show the model predictions assuming step density profile, for (blue), (green) and (red); the corresponding predictions without the step function profile assumption, calculated with SCFT are shown in dots of the same color (Opferman et al., 2012; 2013). Despite small numerical differences, the trends predicted by the two models are the same. Similarly, the step density profile does not affect the pertinent theory predictions in the presence of nanoparticles in relevant regime (Opferman, 2014).
Figure 3
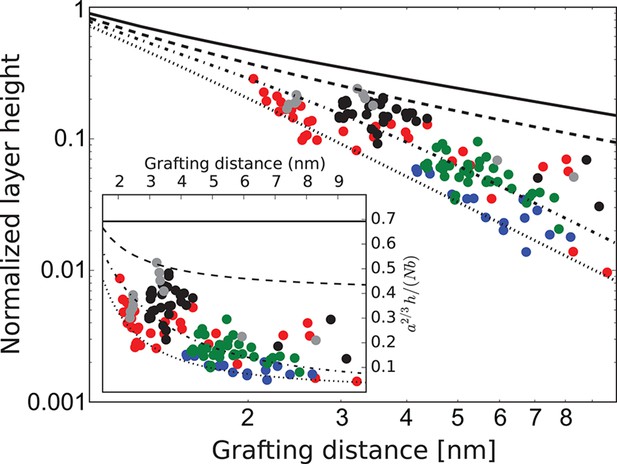
FG nup layer height depends on the grafting distance: theory vs. experiment.
The dots are the experimentally measured layer heights from Kapinos et al. (2014) and Wagner et al. (2015) normalized by the FG nup length. Red, blue, green and black: grafted layers of Nup62, Nup98, Nup153 and Nsp1, respectively; gray dots belong to a short Nsp1 segment. Solid line: is the ideal brush () behavior obtained from the model. Dotted line: is the behavior of a strongly collapsed brush with . All the FG Nups lie between these two regimes, indicating a significant amount of cohesion for all FG nups; the dashed line is for ; the dashed-dotted line is for . To enhance the contrast, inset shows the same data with the height normalized by the ideal brush height. nm, nm.
Figure 4 with 1 supplement
Characteristic responses of FG nup layers to the transport proteins: experimental results.
Upper panel: change in the layer height relative to the unperturbed layer as a function of the transport protein concentration in the outside solution. Lower panel: number of the transport proteins in the layer per unit length of the FG nup chain. Each line corresponds to a different run with a different initial layer height and grafting distance. Different colors correspond to different FG nups, which all exhibit qualitatively similar behavior. Color coding. Red, blue, green and black: Karyopherin- interacting with Nup62, Nup98, Nup153 and Nsp1, respectively; magenta: NTF2 interacting with Nsp1. The corresponding average grafting distances are nm, nm, nm, nm. The data are from Refs. (Kapinos et al., 2014; Wagner et al., 2015)
Figure 4—figure supplement 1
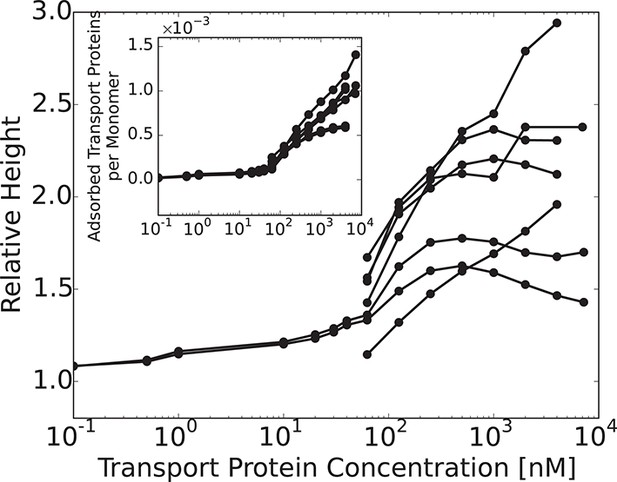
Nup214.
Experimentally obtained normalized height of Nup214 layer vs. Kap- concentration in the solution. The inset shows the number of adsorbed Kap- molecules per monomer as a function of their concentration in solution. Data from Ref. (Kapinos et al., 2014). Behavior of Nup214 qualitatively obeys the same 'bi-phasic' pattern as the rest of the studied FG nups and lies within the landscape of behaviors predicted by the model. However, it is plotted separately because the experimental data is sparse at low concentrations and is highly variable at high concentrations. Multiple reasons can possibly account for this behavior, analysis of which lies outside the scope of the present work.
Figure 5
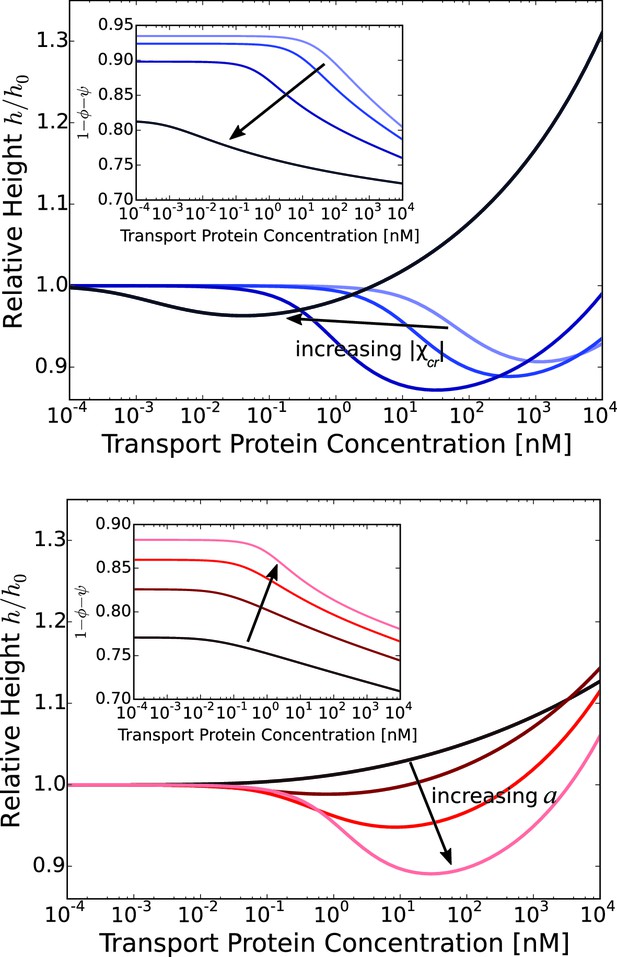
Layer collapse and swelling: effect of cohesion and of the grafting distance.
Upper panel: Theoretical curves show that FG nup cohesion can convert layer collapse to swelling. The cohesion strengths are for nm and . Lower panel: Increasing grafting distance increases the magnitude of the layer compaction. The lines correspond to model predictions for nm for and . The insets show that the fraction of free space in the layer, calculated as , decreases with the addition of the transport proteins. nm, nm in both panels.
Figure 6 with 1 supplement
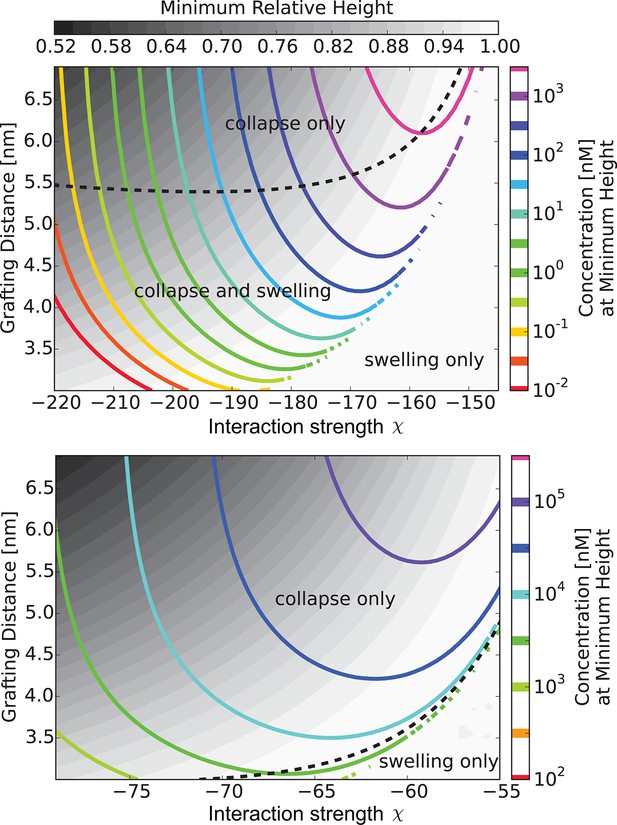
The 'phase diagram' of predicted behaviors: conformational transitions of the layer.
The grayscale color denotes the degree of layer compaction, , relative to the unperturbed layer (color legend is on top). The colored contour lines indicate the corresponding bulk concentration at which the minimal layer height is achieved (legend on the right side). There is no layer swelling above the dashed line (up to 1 M transport protein concentration). Upper panel: , roughly corresponding to Karyopherin-; Lower panel: , roughly corresponding to NTF2. The overall phase diagram topology is similar in both cases, but for smaller protein the collapse is more pronounced and occurs at lower interaction strengths . In both panels nm, corresponding to the 'monomer' size of roughly four amino acids.
Figure 6—figure supplement 1
Model predictions are robust with respect to the monomer size estimate.
We have performed extensive sensitivity analysis of the model with respect to the choice of the molecular parameters. It is illustrated in the phase diagram as a function of the grafting distance and the interaction strength with a different parameter choice, . The topology of the phase diagram is the same as in Figure 6, and the same qualitative trends are observed in both cases, with three regions of behaviour: 'collapse only', 'collapse and swelling', and 'swelling only'; the agreement with the experimental data is also of a similar quality.
Figure 7
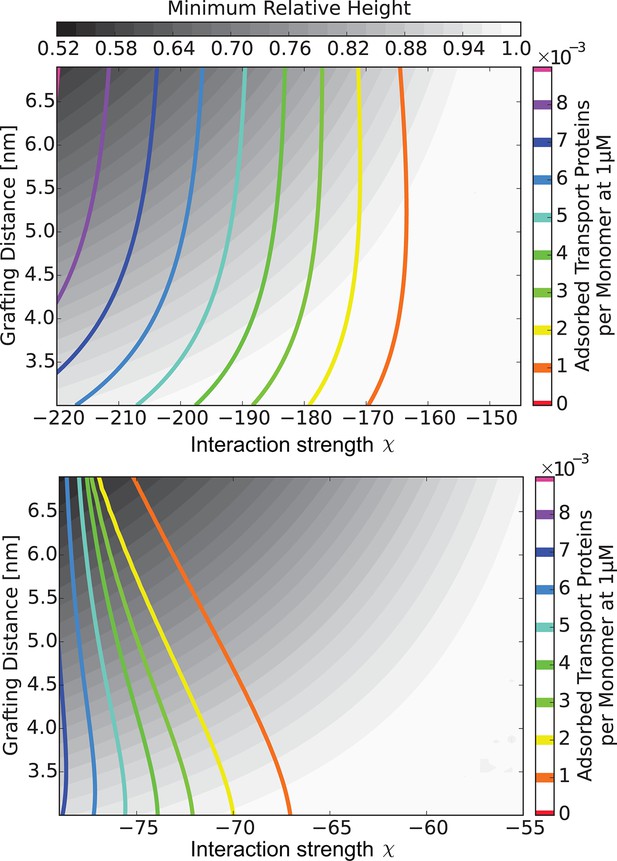
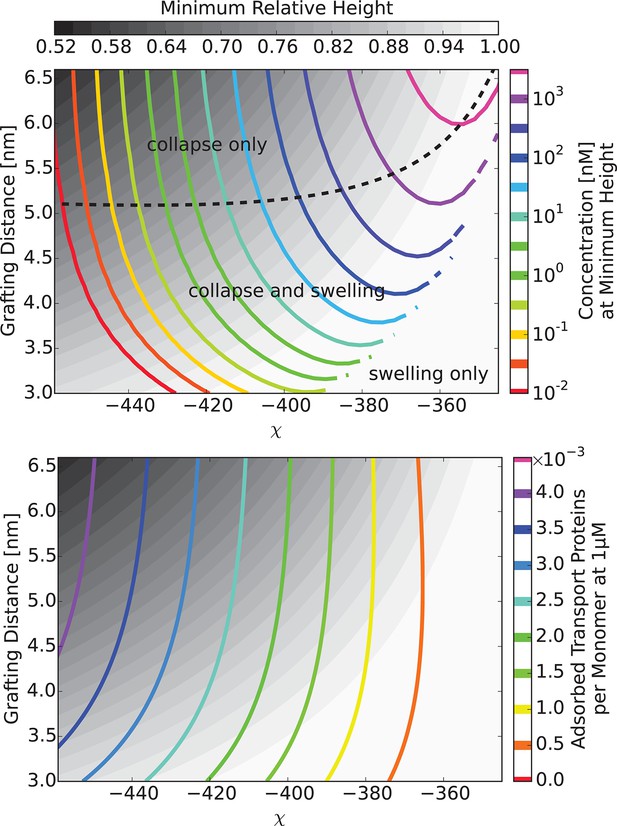
The 'phase diagram' of predicted behaviors: amount of transport protein in the layer.
The grayscale color denotes the degree of layer compaction, , relative to the unperturbed layer (color legend is on top). The colored contour lines show the amount of adsorbed proteins in the layer per chain monomer. Higher degree of collapse is correlated with higher accumulation of the proteins in the layer. Upper panel: , roughly corresponding to Karyopherin-; Lower panel: , roughly corresponding to NTF2. In both panels nm.
Figure 8 with 1 supplement
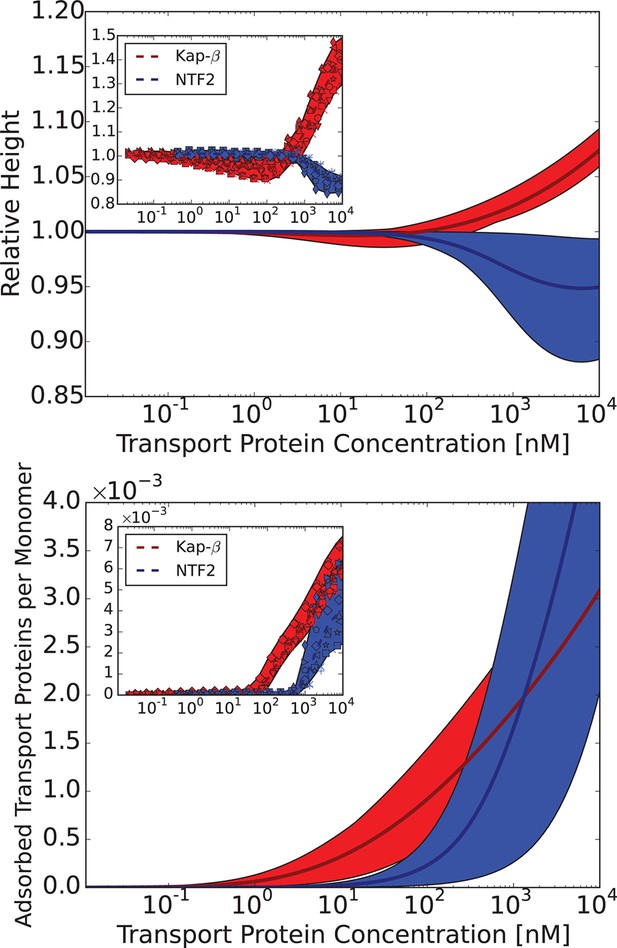
Comparison of the theoretical predictions with the experimental data in the layer geometry.
Theoretical predictions for the range of the parameter values approximately corresponding to the experimental ones for Nsp1 layers infiltrated by Karyopherin- and NTF2. Upper panel: layer height vs bulk concentration of the transport protein. Red: Karyopherin-, Blue: NTF2. Lower panel: amount of adsorbed transport protein in the layer as a function of the concentration in the solution. Red: Karyopherin-, Blue: NTF2. The shaded regions correspond to nm and for NTF2 and for Karyopherin- . For all lines, nm and . The insets show the corresponding experimental data from Wagner et al. (2015).
Figure 8—figure supplement 1
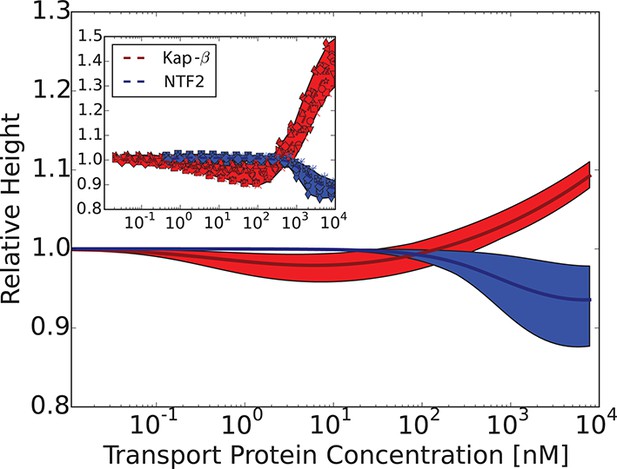
Model predictions are robust with respect to the monomer size estimate.
We have performed extensive sensitivity analysis of the model with respect to the choice of the molecular parameters. As an illustration, predictions of the theory for are compared with the experimental data from Kapinos et al. (2014); the agreement is of a similar quality.
Figure 9
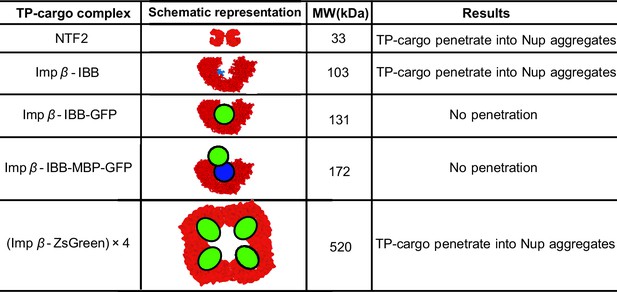
Partitioning of transport proteins into dense FG nup phase: summary of experimental results.
Experimentally, partitioning of the transport proteins (TP) complexes with various cargoes into the dense FG nup phase depends on the cargo size and the overall interaction strength of the complex with the FG nups. Both Importin- (vertebrate homologue of Kap-) and NTF2 penetrate the dense phase, but the Importin- with either medium (IBB-GFP) or large (IBB-MBP-GFP) cargo does not. However, the very large complex of four Importin- complexed with four ZsGreen proteins partitions into the dense phase. The results are for the dense phase of TtNup98 of Tetrahymena Thermophila recombinantly expressed in bacteria, adapted from Schmidt and Görlich (Schmidt and Görlich, 2015).
Figure 10 with 1 supplement
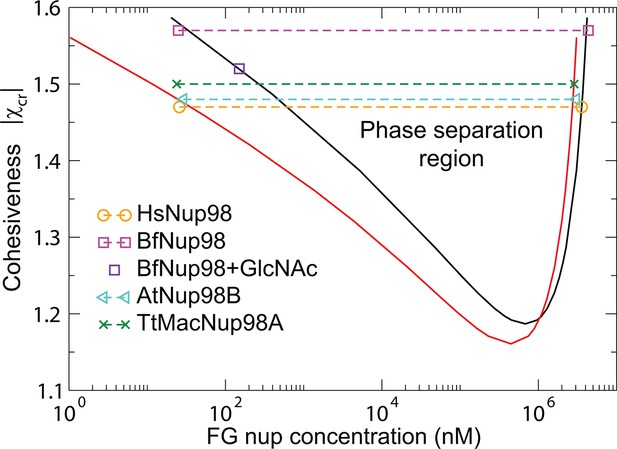
Phase separation in FG nucleoporin solutions: theory vs. experiment.
For combinations of and FG nup concentrations that lie above the phase separation boundaries shown in solid lines, the system undergoes a phase separation into the dilute and the dense phases that lie on the boundaries of the phase separation region. The symbols show the experimentally estimated concentrations of Nup98 from different species in the co-existing dilute and dense phases from Schmidt and Görlich (2015). The phase separation boundaries are calculated with the following parameters: N=125 monomers (black) and N=167 monomers in the chain (red), nm3, nm, corresponding to approximately four amino acids per monomer.
Figure 10—figure supplement 1
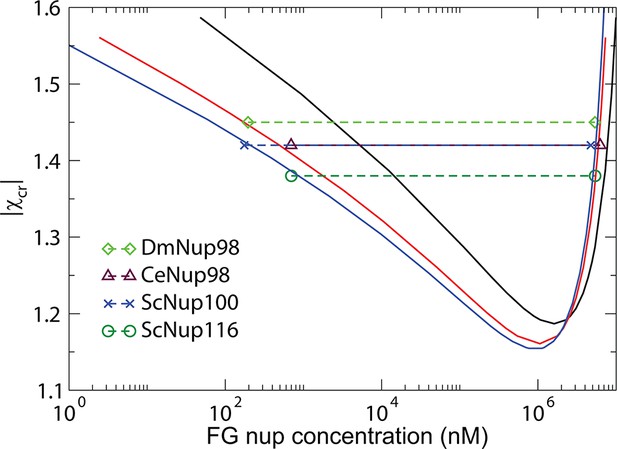
Phase separation of Nup98s from the remaining two species as well as of yeast nucleoporins ScNup100/ScNup116 from Schmidt and Görlich (2015) can also be accommodated within the theoretical model, with slightly different packing fraction and monomer volume.
These differences reflect potentially different morphologies and structures of the dense phase that are currently unknown. Molar concentrations of the dilute and the dense phases of the FG nup constructs constructs are from Table 1 of Ref. Schmidt and Görlich (2015). Black, red and blue curves are the theoretically predicted coexistence curves, computed with , corresponding to roughly - amino acids per monomer for the corresponding FG nups. Monomer volume and the maximal packing fraction is .
Figure 11 with 1 supplement
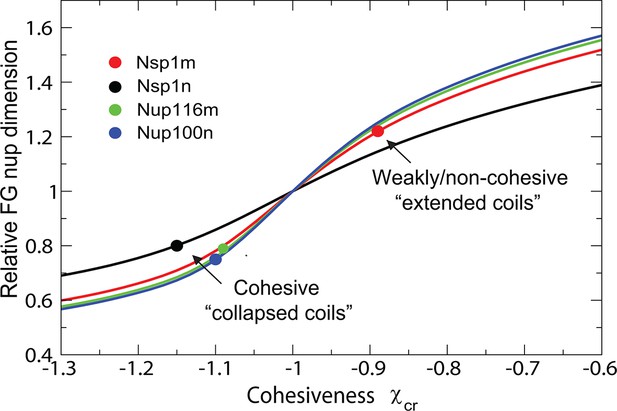
Dimensions of individual FG nucleoporins in solution: theory vs. experiment.
Comparison of the model predictions for the dimensions of individual FG nups with the observations of Yamada et al (Yamada et al., 2010). Dimensions of the individual FG nup coils are normalized by the dimensions of the Gaussian chain of the same length ('relaxed coil' for the experimental data). Solid black, red, green and blue lines are the theoretical model predictions for corresponding to four amino acids per monomer for the respective FG nups. The model predictions are independent of the choice of the monomer size . Circles: experimental measurements of the FG nup dimensions from Yamada et al. (2010). Polymer model captures the bimodal distribution of 'extended' and 'collapsed' FG nups. This behavior, known as the coil-globule transition in polymer literature, reflects physically the same phenomenon as the decrease in the grafted layer height with increase in cohesiveness strength shown in Figure 2.
Figure 11—figure supplement 1
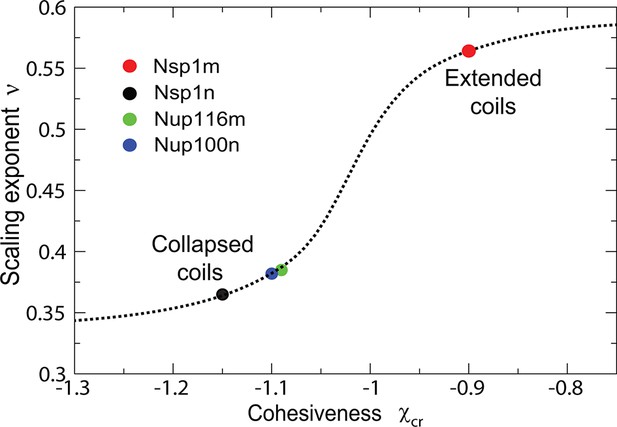
Classification of individual FG nucleoporins according to their scaling exponent.
Intrinsically disordered proteins can be classified into different types based on the effective scaling exponent of the scaling relationship of the chain dimension with the chain length, (Tcherkasskaya et al., 2003). Cohesiveness determines the scaling exponent and allows categorization of the FG nups into into 'extended' vs 'collapsed' coils as a function of the cohesiveness ; for extended coils while for collapsed globules (Tcherkasskaya et al., 2003). Dotted line: theoretical model prediction; circles: data from Yamada et al. (2010). Theoretical model assumes four amino acids per monomer and its predictions are independent of the value of the monomer size .
Figure 12 with 1 supplement
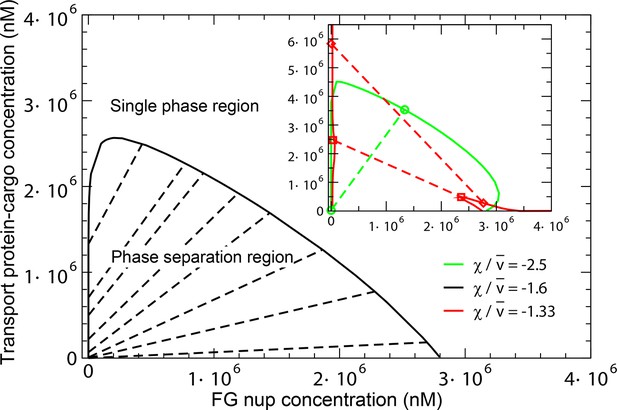
Phase separation in solutions of FG nups mixed with transport proteins: theoretical predictions.
For high enough values of the ratio , mixtures of FG nucleoporins and the transport proteins phase separate into a dense aggregate containing both nups and transport proteins, and a dilute solution. The black line encloses the predicted phase separation region approximately corresponding to a mixture of Imp- and Nup98 calculated at , , , and . The oblique lines connect the coexisting phases that lie on the boundary of the region. Outside of this region, FG nups and transport proteins are homogeneously mixed and no phase separation occurs. Inset: Increasing the transport protein size or decreasing hinders their penetration into the dense phase and eventually leads for their complete exclusion as shown in the red dashed lines connecting the co-existing phases: concentration of the transport proteins in the dense phase is lower than outside. Vice versa, increasing enhances the penetration of the transport proteins into the dense phase as shown in the green lines.
Figure 12—figure supplement 1
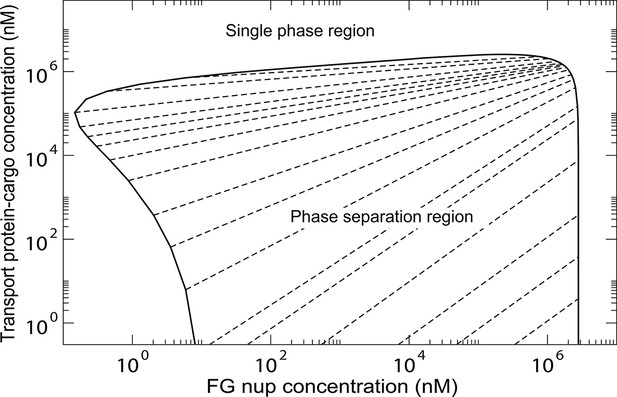
Phase separation region of Figure 12 in a double logarithmic scale.
The oblique dashed lines connect the coexisting phases that lie on the boundary of the region. Outside of this region, FG nups and transport proteins are homogeneously mixed and no phase separation occurs.
Figure 13 with 1 supplement
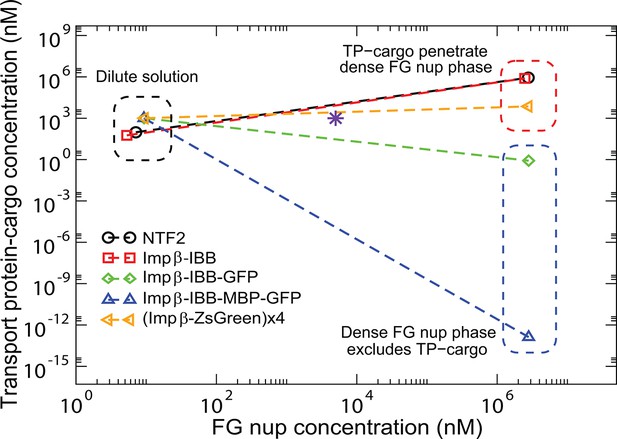
Transport protein partitioning into dense FG nup phase: theory vs.
experiment. Theoretical model captures the pattern of partitioning of the transport proteins into the dense phase. Symbols connected with dotted lines show the theoretically predicted co-existing dilute and dense phases of TtNup98 at varying sizes of transport protein-cargo complexes corresponding to those used in Schmidt and Görlich (2015) and summarized in Figure 9. Transport proteins Importin- and NTF2 partition into the dense phase, while larger complexes of Importin- with different cargoes do not. Even a large cargo can be configured to penetrate the dense phase as illustrated by the example of a tetramer of Imp--ZsGreen complexes. All theoretical solutions are for the initial concentrations of M of Nup98A and M of the transport protein-cargo complexes (indicated by the pink star symbol). Parameters used to generate these solutions are established from the analysis of Nup98 phase separation in the absence of the transport proteins, described in Figure 10: N=167, nm3, ; see text for the interaction parameters of the transport proteins with the FG nups .
Figure 13—figure supplement 1
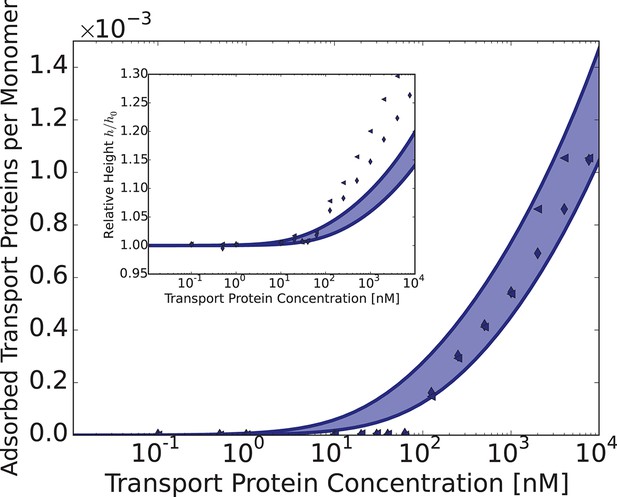
Adsorption of Karyopherin- into Nup98 layer and the layer height (inset) vs. bulk concentration of Kap-.
The shaded region corresponds to theoretical predictions at nm, , and nm, nm. The points show the corresponding experimental data for human Nup98 from Kapinos et al. (2014). The surface layer of Nup98, studied in Kapinos et al. (2014) is described by a very close set of parameters as the phase separation in bulk solutions of Nup98 described in Schmidt and Görlich (2015). Small differences in the value of are expected and can be attributed to the differences in experimental conditions.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Simple biophysics underpins collective conformations of the intrinsically disordered proteins of the Nuclear Pore Complex
eLife 5:e10785.
https://doi.org/10.7554/eLife.10785
