Distinct functional determinants of influenza hemagglutinin-mediated membrane fusion
- University of Colorado, United States
- Harvard Medical School, United States
- Brandeis University, United States
- Howard Hughes Medical Institute, Harvard Medical School, United States
Figures
Figure 1
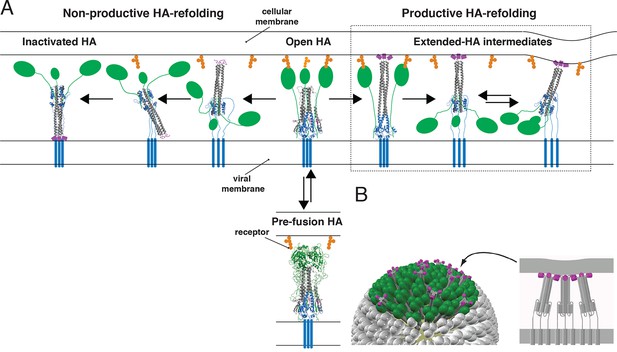
Productive and non-productive HA refolding, and membrane fusion by cooperative action of multiple, stochastically triggered HAs.
(A) Proton binding increases the relative time HA spends in the ‘open’ conformation allowing fusion peptides to project toward the target membrane. HA1 is shown in green and HA2 in magenta (fusion peptides), gray (N-terminal ‘half’) and blue (C-terminal ‘half’). Right-hand arrow: Productive HA refolding proceeds through an extended-intermediate state with fusion peptides inserted in the target membrane (Ivanovic et al., 2013). We illustrate a possibility that membrane-engaged HAs might represent an ensemble of folded-back conformations; the corresponding distance between the two membranes might fluctuate around a different value depending on how many HAs are cooperating. Left-hand arrow: Non-productive HA-refolding event occurs if HA assumes the low-pH form without target membrane engagement, resulting in loss of that HA as a potential fusion participant. (B) Individual-HA triggering and membrane insertion occur at random within a larger virion area that contacts the target membrane (~50 HAs shown in green are contained within this interface for a small, spherical influenza virion [Ivanovic et al., 2013]). Fusion ensues once a sufficient number of HAs – as needed to overcome the resistance of membranes to bending and apposition – are pulling jointly on the same membrane region (Ivanovic et al., 2013). 3D coordinates (PDB ID) used for displayed HA cartoons: the pre-fusion HA (2HMG), inactivated HA (1QU1); depicted intermediates are derived from a subset of either or both sets of coordinates (2HMG and/or 1QU1).
Figure 2 with 1 supplement
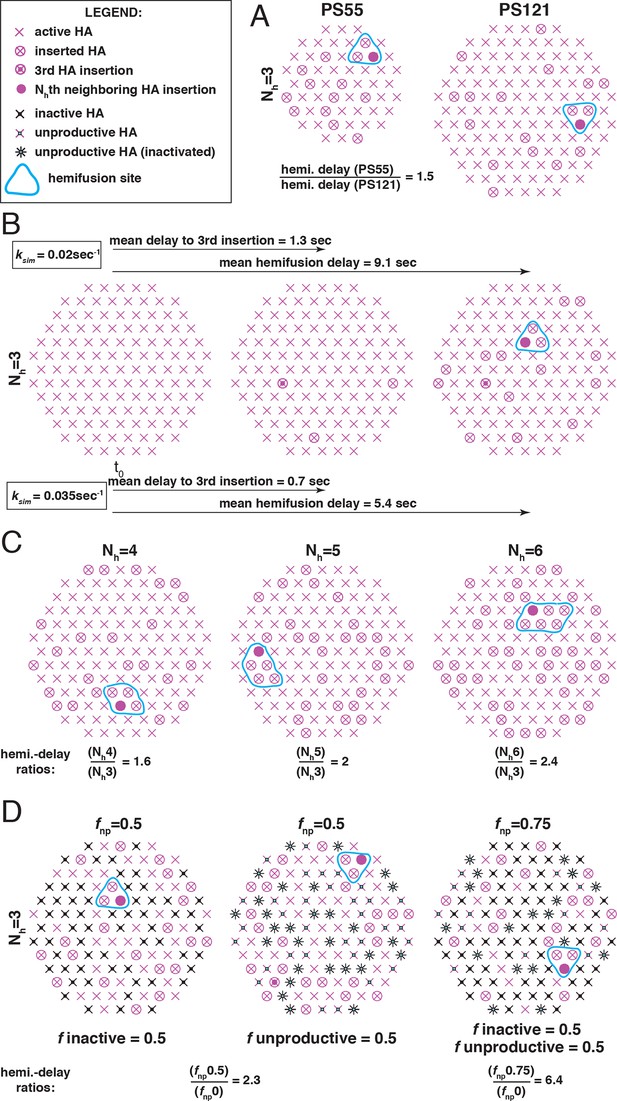
The functional variables of influenza membrane fusion modeled in this work.
We modeled the kinetics and the extent of membrane fusion with the following parameters: (A) the number of HAs in contact with the target membrane (patch size, PS), (B) the rate (ksim) of stochastic HA triggering, (C) the required number (Nh) of cooperating HA neighbors during fold-back (see Figure 2—figure supplement 1 for the complete definition of six-mers (Nh = 6) in the simulation), and (D) the frequency of inactive (left) or unproductive (middle) HAs, combined in the common parameter fnp (right) as described in Materials and methods. Illustrations represent sample contact patches at the times of hemifusion except in panel B (left and middle), where they represent earlier time points. We compare the effects of various functional variables by either showing the ratios of mean hemifusion delays (ksim-independent values) (A, C and D), or by directly showing mean hemifusion delays for two ksim values, and PS = 121, Nh = 3 and fnp = 0 (B). Our fusion model predicts that smaller patch size, lower ksim, higher Nh, or higher fnp, will each increase hemifusion delay, and, with the exception of ksim, will also, under certain conditions, reduce the theoretical fusion yield (see Figure 3).
Figure 2—figure supplement 1
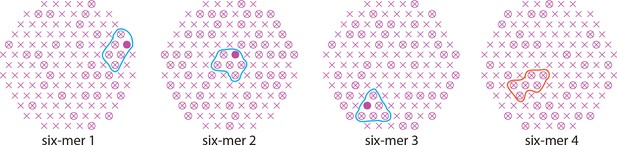
Definition of six-mers (Nh = 6) in the simulation.
Since multiple HAs must fold back cooperatively, possible six-mers have distinct properties: two groups of three HAs that can join around either two adjacent or one wider target-membrane deformation (six-mers 1 and 2); HAs that all surround the same central target-membrane deformation (six-mer 3). Because HAs must fold away from the membrane deformation (see illustration in Figure 1, the productive path), six-mer 4 will tend to act as two isolated groups of three HAs or, more likely, as a tetramer with two nearby HAs that are not close enough to join their efforts in pulling on the same target-membrane area.
Figure 3 with 3 supplements
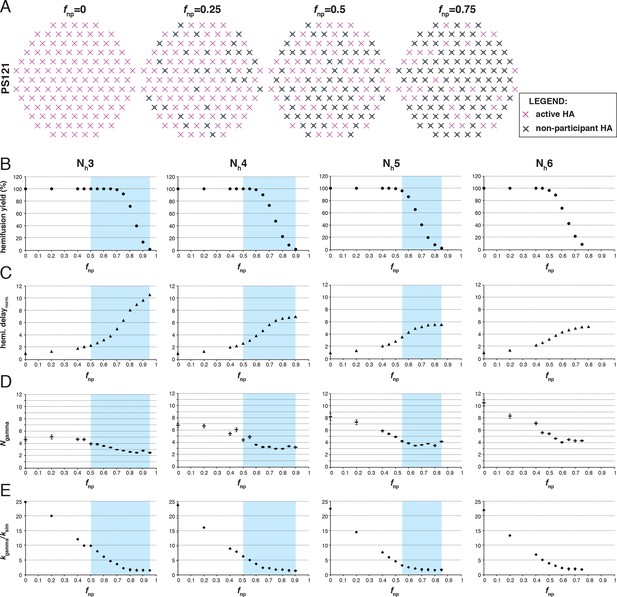
Effects of fnp on hemifusion yield and kinetics for Nh = 3–6 (PS = 121).
(A) Illustration of simulated contact patches. (B) Hemifusion yield as a function of fnp. (C) Mean hemifusion-delay times normalized to fnp = 0. (D) Parameter N derived from fitting hemifusion delay distributions with the gamma probability distribution. Errors are 95% confidence intervals for the fit-derived values. (E) Parameter k derived from fitting hemifusion delay distributions with the gamma probability distribution expressed as ratio with ksim. By normalizing mean hemifusion-delay times and kgamma, we obtained general trends, independent of the ksim value used in simulations. Plotted results are derived from simulations that yielded 1000–3000 hemifusion events. Blue shaded regions are estimates for the range of fnp values consistent with Ngamma values derived from experiment. The corresponding results for PS = 55 are shown in Figure 3—figure supplement 1. Refer to Figure 3—figure supplement 2 for the simulation results for Nh = 2 and both patch sizes. Refer to Figure 3—figure supplement 3 for Ngamma values derived from our previously published experimental datasets (Ivanovic et al., 2013).
Figure 3—figure supplement 1
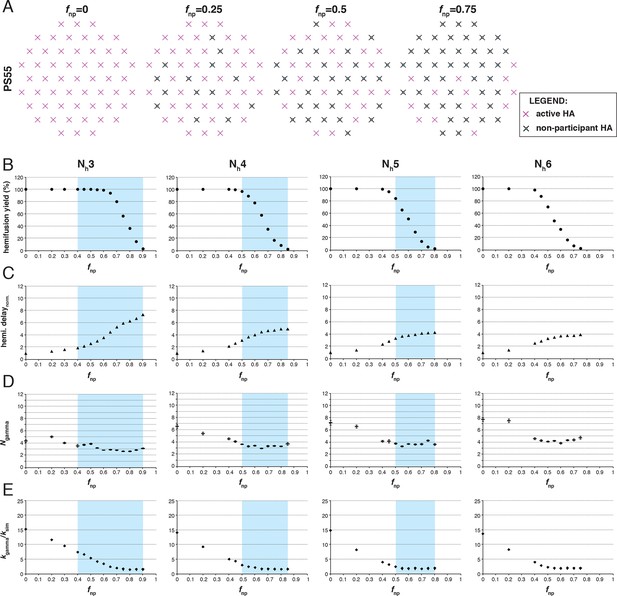
Effects of fnp on hemifusion yield and kinetics for Nh = 3–6 (PS = 55).
Refer to the main Figure 3 legend, which shows results of an analogous set of simulations using PS = 121 instead of PS = 55.
Figure 3—figure supplement 2
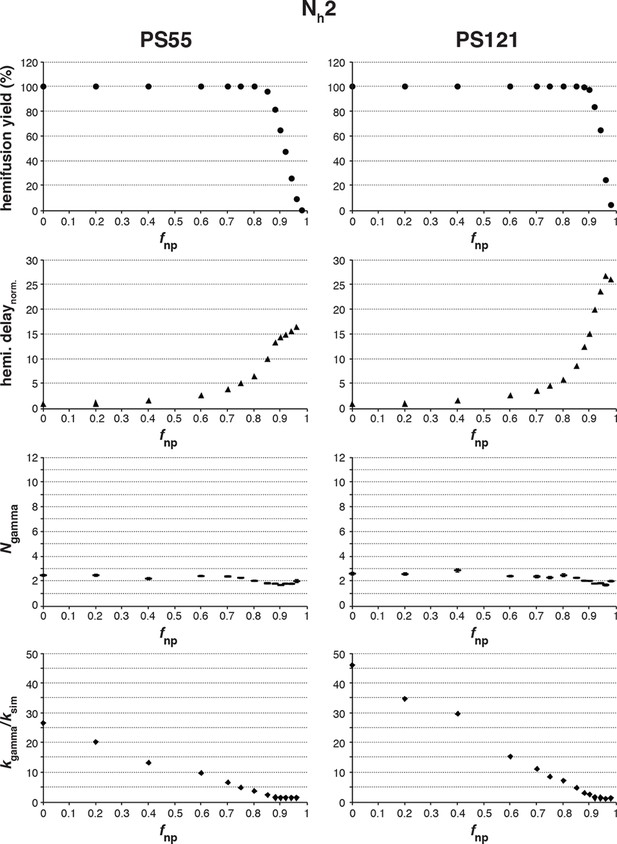
Effects of fnp on hemifusion yield and kinetics for Nh = 2.
Simulation results for both PS = 55 and PS = 121 are shown. Hemifusion yield (top row), mean hemifusion-delay times normalized to fnp = 0 (second row), parameter N derived from fitting hemifusion delay distributions with the gamma probability distribution (third row), and parameter k derived from fitting hemifusion delay distributions with the gamma probability distribution expressed as ratio with ksim (bottom row). The simulation results for Ngamma when Nh = 2 are inconsistent with previous experiments that routinely report values of 3 or higher (please refer to Figure 3—figure supplement 3). This comparison further validates our original conclusion that Nh > 2, from experimental data that appeared to rule it out (Ivanovic et al., 2013).
Figure 3—figure supplement 3
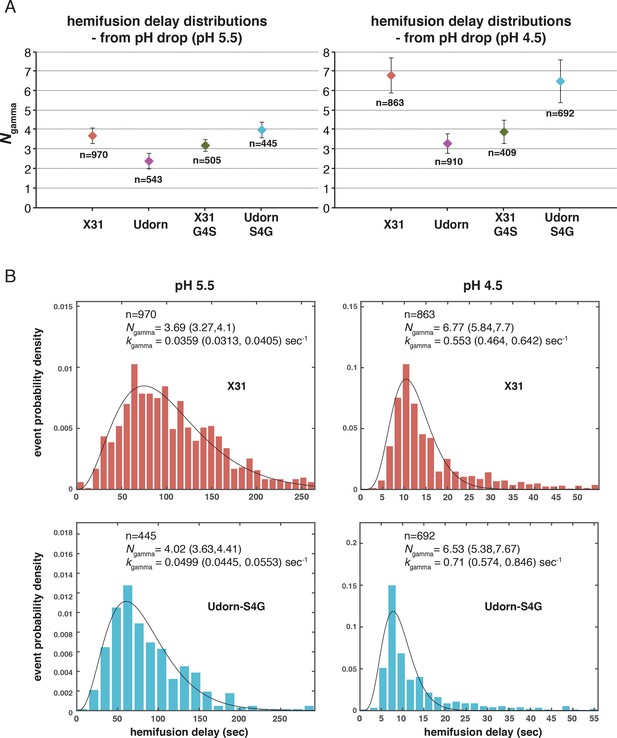
Ngamma for pH-drop-to-hemifusion frequency distributions from previously published experiment data (Ivanovic et al., 2013).
Udorn and X31-G4S are previously published values. X31 and Udorn-S4G are newly determined values from those published datasets. (A) Ngamma values with 95% confidence intervals (error bars) for the fit-derived values. (B) Frequency distributions for the newly derived values fitted with the gamma distribution. 95% confidence intervals for the fit-derived values are shown as a range of values in parentheses. Samples that resulted in larger Ngamma values (Ngamma>4) also yielded poorer fits.
Figure 4 with 1 supplement
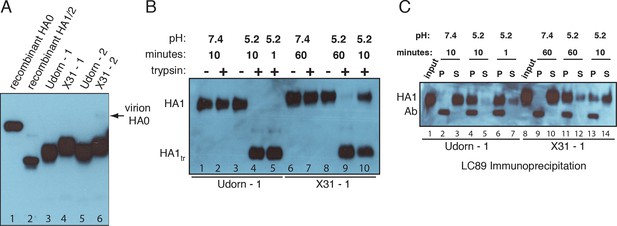
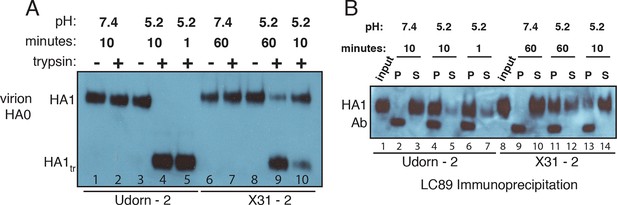
Complete processing of virion-associated HAs and complete conformational change at low pH.
We show WT UdornHA-Udorn and X31HA-Udorn virions used in our previous single-virion fusion experiments (Ivanovic et al., 2013). SDS-PAGE and western blot of virions probed with HA1-specific antibody that detects both HA0 and HA1 alone. (A) Recombinant X31 HA0 and HA1:HA2 are included as a reference. The various HA forms appear to show varying levels of glycosylation resulting in different gel migration patterns. A trace amount of unprocessed HA0 is apparent in only one of two X31HA-Udorn preparations (lane 6, band location marked with an arrow). (B,C) Virions were incubated in either neutral or pH5.2 buffer for indicated times at 37°C. (B) Virions were either loaded directly onto the gel or treated with trypsin prior to loading. Resistance to trypsin digestion of virion-HA incubated in neutral buffer is a control for pre-fusion HA integrity. HA1tr is the trypsin-resistant fragment of HA1 (C) Virions were immunoprecipitated with LC89 antibody (specific for the low-pH form of HA2 [Wharton et al., 1995]), and the entire bead-associated fraction (P) and the supernatant (S) were loaded onto separate lanes of the gel. Ab refers to the band corresponding to the heavy chain of the antibody used for immunoprecipitation, detected with the secondary antibody used in the western blot. Complete HA conversion to trypsin-sensitive form or to a form that can be immunoprecipitated with LC89 antibody is apparent by 1 min for Udorn HA and by 60 min for X31 HA. The conversion kinetics for X31-HA are disproportionately slower than its fusion kinetics (Ivanovic et al., 2013); see the Discussion for consideration of the consequences of these observations for the fusion mechanism. An analogous set of results for the second UdornHA-Udorn and X31HA-Udorn clones are shown in Figure 4—figure supplement 1.
Figure 4—figure supplement 1
Complete processing of virion-associated HAs and complete conformational change at low pH.
See main Figure 4, panels (B,C) legend, showing an analogous experiment performed with a different set of UdornHA-Udorn and X31HA-Udorn clones.
Figure 5 with 1 supplement
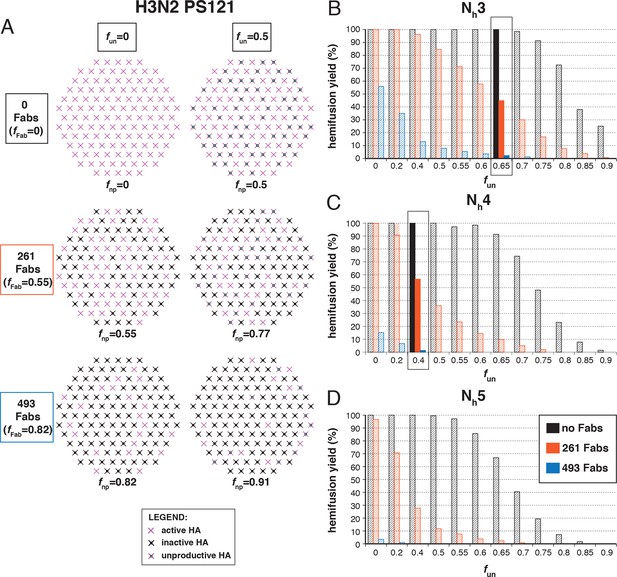
Hemifusion yield as a function of the fraction of unproductive HAs (fun) for virions with no bound antibody and for those with 261 or 493 bound Fabs (PS = 55).
(A) Illustrations of simulated contact patches. The frequency of Fab-bound HAs (fFab) and fun were combined in the parameter fnp as described in Materials and methods. (B–D) The results for Nh = 3 (B), Nh = 4 (C), and Nh = 5 (D) were derived from simulations that yielded 1000-3000 hemifusion events. Non-zero fun values (boxed out regions in (B) and (C) are required to explain the experimentally observed number of Fabs required for half-maximal (261) and maximal (493) inhibition of H3N2 X31 influenza virus hemifusion (Otterstrom et al., 2014). Experimental data are inconsistent with Nh = 5. The corresponding results for PS = 55 are shown in Figure 5—figure supplement 1.
Figure 5—figure supplement 1
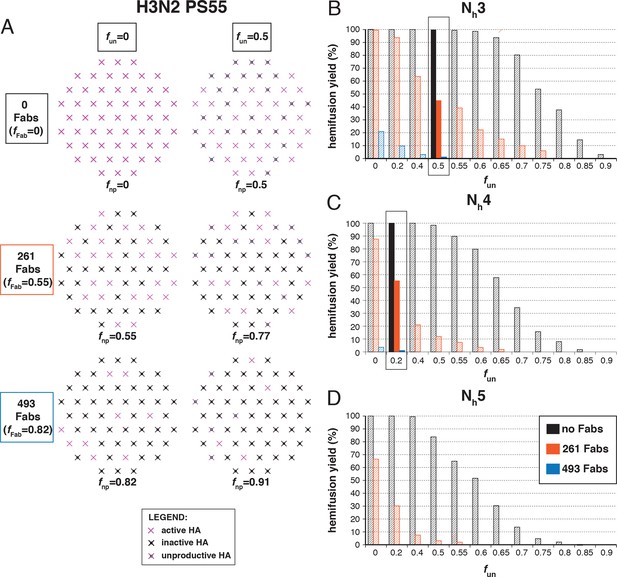
Hemifusion yield as a function of the fraction of unproductive HAs (fun) for virions with no bound antibody and for those with 261 or 493 bound Fabs (PS = 121).
See main Figure 5 legend which shows results of an analogous set of simulations using PS = 121 instead of PS = 55.
Figure 6 with 3 supplements
Effects of Fab binding on hemifusion yield and kinetics for given pairs of Nh and fun (PS = 121).
(A) Illustrations of simulated contact patches at the time of hemifusion for several fnp values (fun was kept constant while fFab was increased). (B–E) Comparison of simulation-derived results (1000–3000 hemifusion events) for hemifusion yield (B), hemifusion delay (geometric mean) (C), Ngamma (D) and kgamma (E) with experimental data for H3N2 X31 influenza from Otterstrom et al. (2014) (black triangles). Experimental hemifusion yield data in (B) (their Figure 2C) were scaled so that the highest measured hemifusion yield value became 100% (i.e. each data point was multiplied by 4/3). The corresponding results for PS = 55 are shown in Figure 6—figure supplement 1. For simulations testing the effect of sample size on variability in Ngamma, see Figure 6—figure supplement 2. For a further test of the robustness of the conclusions derived from this figure, see Figure 6—figure supplement 3.
Figure 6—figure supplement 1
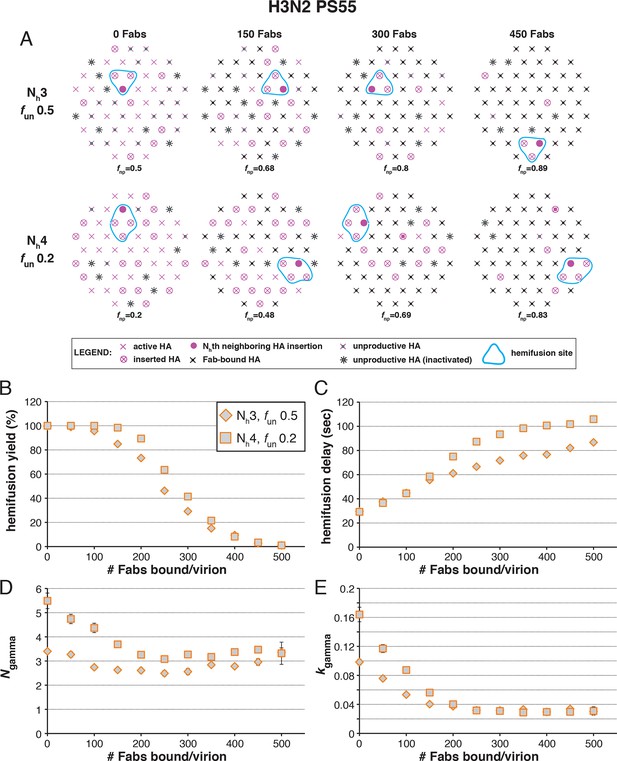
Effects of Fab binding on hemifusion yield and kinetics for given pairs of Nh and fun (PS = 55).
See main Figure 6 legend, which shows results of an analogous set of simulations using PS = 121 instead of PS = 55. For the adjusted values of fun, PS = 55 data are indistinguishable from PS = 121 data.
Figure 6—figure supplement 2
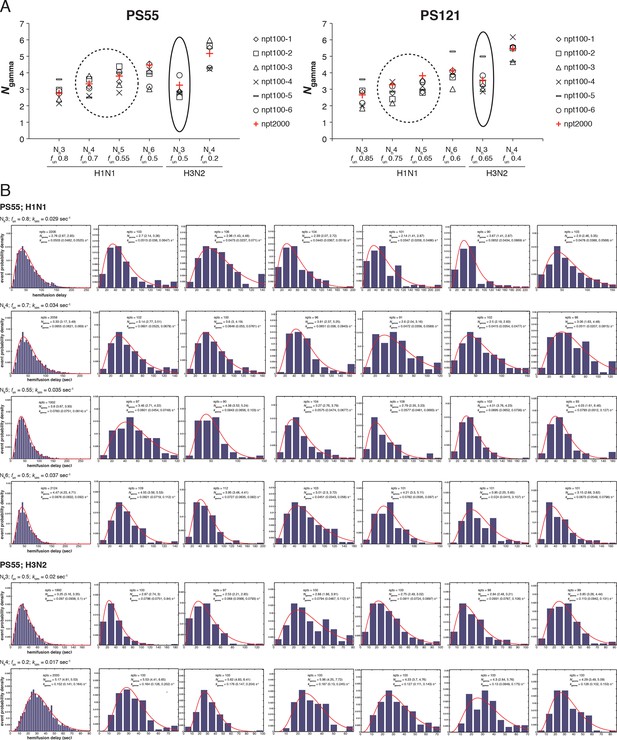
Effect of sample size on variability in Ngamma.
We derived Ngamma values for 6 small datasets and a single large data set for both PS = 55 and PS = 121 and for each pair of Nh and fun identified for H3 X31 and H1 PR8 HAs in Figure 5 and 7, respectively. (A) Plots showing derived Ngamma values for small datasets (black symbols, n~100) and large datesets (red pluses, n~2000). Circled results are derived using the functional parameters (Nh and fun) that best agree with Otterstrom et al. (2014) data. (B) Individual histograms for PS = 55 data that went into plots shown in (A).
Figure 6—figure supplement 3
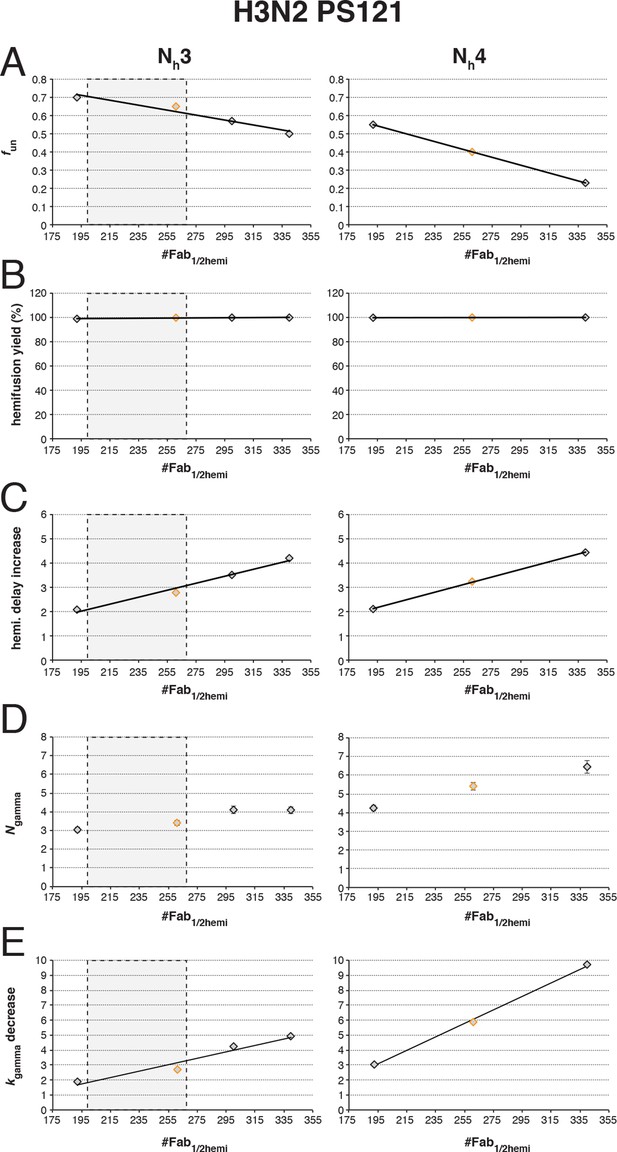
Effects on our conclusions of potential error in the measurement of the number of Fabs needed for 50% hemifusion inhibition (#Fab1/2hemi) for H3N2 X31 influenza virions.
For the simulation results shown, we included several #Fab1/2hemi values covering the entire 95% confidence interval for this measurement (Otterstrom et al., 2014). (A) fun required to give half-maximal inhibition in the hemifusion yield. Each data point on this plot represents the result of a separate analysis, either shown as red bars in Figure 5 (orange diamonds) or an analogous result derived for each new #Fab1/2hemi value (black diamonds). (B–E) Subsequent analyses then used the fun:Nh pairs determined in (A) to repeat simulations shown in Figure 6 – fun was kept constant, while fFab was increased. We expressed results from Figure 6, panels (B-E) (orange diamonds) and from these new analogous titrations (black diamonds) each as a single value: (B) hemifusion yield for virions with no bound Fab, (C) increase in hemifusion-delay over the entire range of bound Fabs, (D) Ngamma for virions with no bound Fab, and (E) decrease in kgamma over the entire range of bound Fabs. We found that even the lowest value for #Fab1/2hemi did not include the possibility of 4 HAs participating in hemifusion, as the value of Ngamma (D) and decrease in kgamma (E) from simulations fit poorly (compare to experimentally derived values shown in Figure 6, black triangles). The results for the increase in hemifusion delay (C) and the kgamma drop (E) limit the acceptable range of #Fab1/2hemi for Nh = 3 to the lower half of the 95% confidence interval (the boxed-out shaded region) (see Figure 6, black triangles). We thus conclude that 3 stochastically triggered HA neighbors cooperate during fold-back, and that fun is between 0.6 and 0.7 (PS = 121). An analogous set of analyses for PS = 55 yielded indistinguishable main conclusions and yielded values for fun between 0.5 and 0.6 (not shown).
Figure 7 with 1 supplement
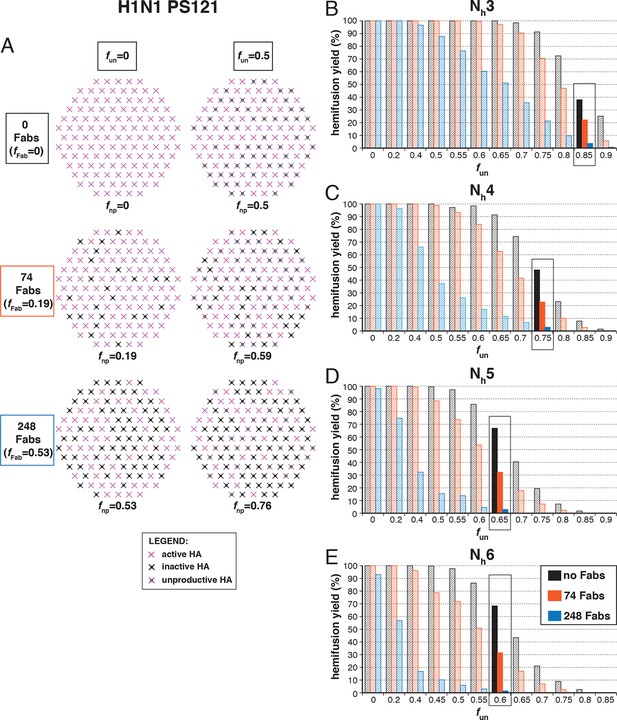
Hemifusion yield as a function of fun for virions with no bound antibody or those with 74 or 248 bound Fabs (PS = 121).
(A) Illustrations of simulated contact patches. (B–E) The results for Nh = 3 (B), Nh = 4 (C), Nh = 5 (D), and Nh = 6 (E) were derived from simulations that yielded 1000 to 3000 hemifusion events. Non-zero fun values (boxed-out regions) are required to explain the experimentally derived number of Fabs required for half-maximal (74) and maximal (248) inhibition of H1N1 PR8 influenza virus hemifusion (Otterstrom et al., 2014). For different fun values, data are consistent with Nh = 3–6. The corresponding results for PS = 55 are shown in Figure 7—figure supplement 1.
Figure 7—figure supplement 1
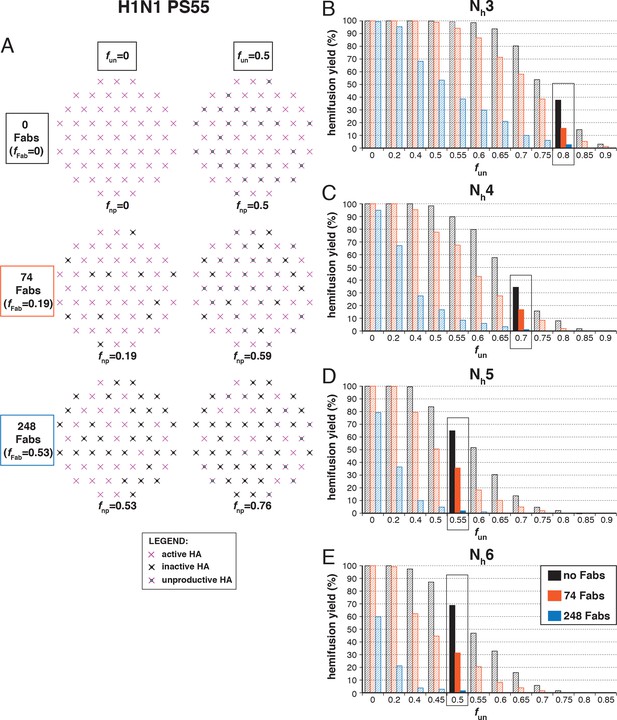
Hemifusion yield as a function of fun for virions with no bound antibody or those with 74 or 248 bound Fabs (PS = 55).
See main Figure 7 legend, which shows results of an analogous set of simulations using PS = 121 instead of PS = 55.
Figure 8 with 2 supplements
Effects of Fab binding on hemifusion yield and kinetics for given pairs of Nh and fun (PS = 121)
(A) Illustrations of simulated contact patches at the time of hemifusion for several fnp values (fun was kept constant while fFab was increased). (B–E) Comparison of simulation-derived results (1000–3000 hemifusion events) for hemifusion yield (B), hemifusion delay (geometric mean) (C), Ngamma (D) and kgamma (E) with experimental data for H1N1 PR8 influenza from Otterstrom et al. (2014) (black pluses). Experimental hemifusion yield data in (B) (their Figure 2C) were scaled using the same factor as in Figure 6B (each data point was multiplied by 4/3). The corresponding results for PS = 55 are shown in Figure 8—figure supplement 1. For a further test of the robustness of the conclusions derived from this figure, see Figure 8—figure supplement 2.
Figure 8—figure supplement 1
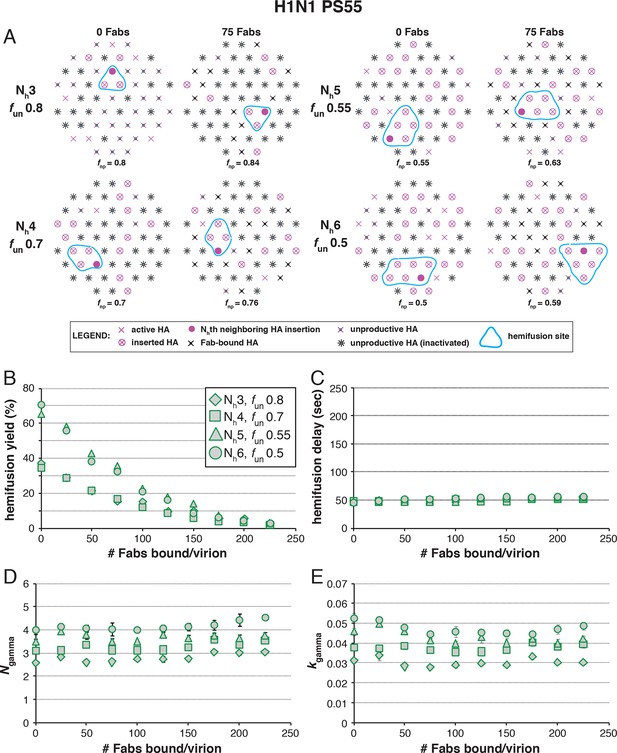
Effects of Fab binding on hemifusion yield and kinetics for given pairs of Nh and fun (PS = 55).
See main Figure 8 legend, which shows results of an analogous set of simulations using PS = 121 instead of PS = 55. For the adjusted values of fun, PS = 55 data are indistinguishable from PS = 121 data.
Figure 8—figure supplement 2
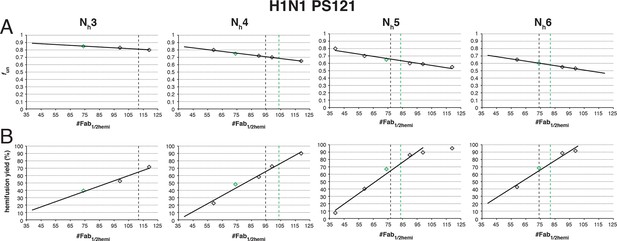
Effects on our conclusions of potential error in the measurement of the number of Fabs needed for 50% hemifusion inhibition (#Fab1/2hemi) for H1N1 PR8 influenza virions.
For the simulation results shown, we included several #Fab1/2hemi values covering the entire 95% confidence interval for this measurement (Otterstrom et al., 2014). (A) fun required to give half-maximal inhibition in the hemifusion yield for each #Fab1/2hemi value. Each data point on this plot represents the result of a separate analysis, either shown as red bars in Figure 7 (green diamonds) or an analogous result derived for each new #Fab1/2hemi value (black diamonds). (B) For each fun:Nh pair determined in (A), we determined the hemifusion yield for virions with no bound Fab. The highest experimentally derived values for the hemifusion yield (65%, black vertical dotted line) (Otterstrom et al., 2014) and the scaled value (75%, green dotted line, see Results for detailed reasoning) are shown where included in the tested range of #Fab1/2hemi values. For Nh = 3, the exclusion of the scaled hemifusion-yield value rules out the interpretation that 3 neighbors cooperate during hemifusion of H1N1 virions. While we cannot exclude Nh = 4 as a possible interpretation, the data are more consistent with Nh = 5 or 6. An analogous set of analyses for PS = 55 yielded indistinguishable main conclusions (not shown).
Figure 9 with 1 supplement
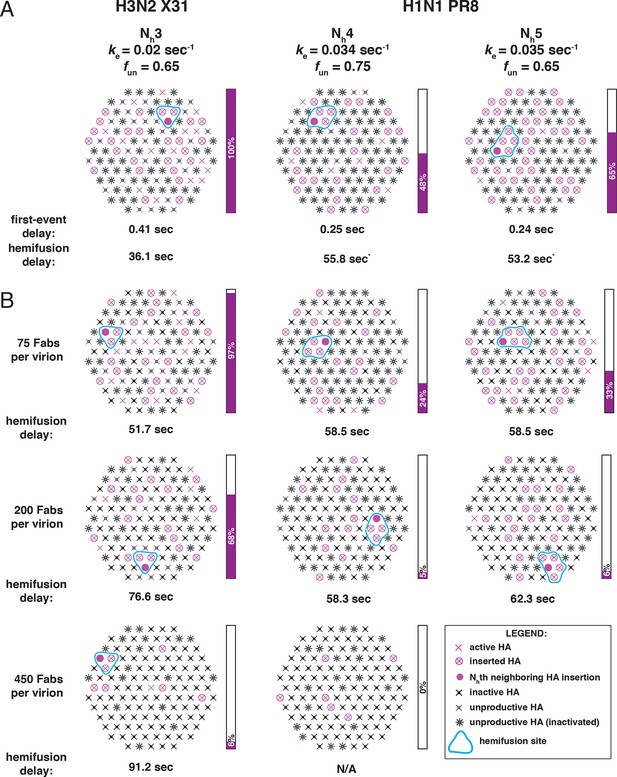
Independent functional determinants of HA-mediated membrane fusion and their effects on the influenza virus susceptibility to neutralization.
Conclusions are presented in the context of the PS = 121 contact patch. (A) The rate of irreversible HA extension (ke) and the frequency of unproductive or inactive HAs determine the rate of target membrane engagement by individual HAs. First-event delay – the average time to the first HA conversion, either productive or non-productive – is determined solely by the ke and the patch size. (See Figure 9—figure supplement 1 for the corresponding model that uses PS = 55). Stochastic HA triggering dictates that small changes in the number (Nh) of HAs required for fold-back have significant effects on the kinetics of fusion. Small increases in Nh significantly reduce the extent of fusion (purple bars) in the context of the large fun values. Compensatory differences in ke, fun and Nh between X31 H3N2 and PR8 H1N1 influenza result in similar overall rates of hemifusion (delay of about 36 and 58 sec, respectively). *Note that by exchanging the ke values between the H3 and H1 functional variables (i.e. compare results for ke = 0.034 sec-1, Nh = 3, fun = 0.65 and ke = 0.02 sec-1, Nh = 4 or 5, fun = 0.75 or 0.65), we obtain ‘extreme’ values for hemifusion delay or ~20 and ~100 sec, respectively. (B) Illustration of the effects of Fab binding on fusion kinetics (mean hemifusion delay) and the theoretical hemifusion yield (purple bars) in the context of functional variables revealed for H3N2 X31 and H1N1 PR8 influenza virions. Our conclusions reveal an intricate link between the molecular features of the evolved fusion mechanism and its susceptibility to neutralization.
Figure 9—figure supplement 1
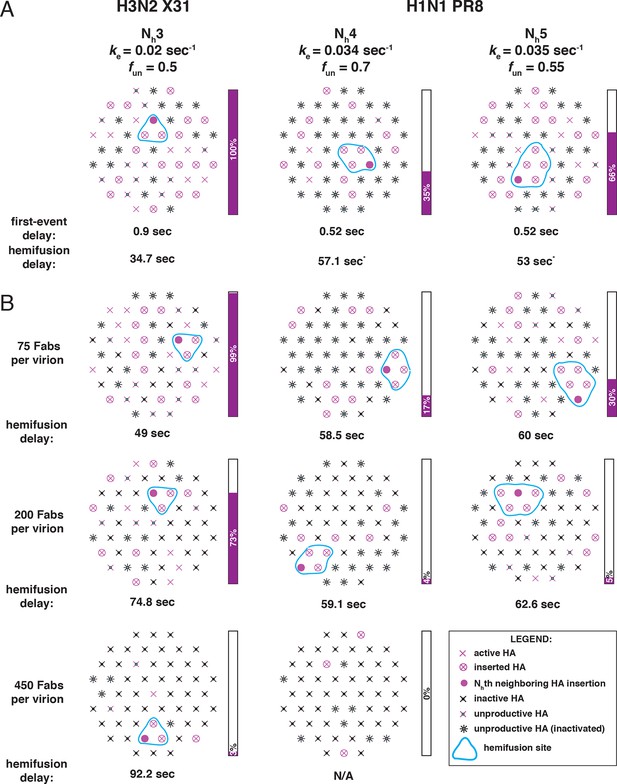
Independent functional determinants of HA-mediated membrane fusion and their effects on the influenza virus susceptibility to neutralization.
Conclusions are presented in the context of the PS = 55 contact patch. See main Figure 9 legend.
Additional files
-
Source code 1
The simulation model of fusogenic molecular events at the virus target-membrane interface.
The code consists of the main code text and four functions written in MATLAB (version R2015a). The main code script is titled s_arrest_hemifusion_simulation_eLife2015resubmission.m, and the functions are generate_patch.m, s_randomdist.m, isaN2tuplet6AllGeos.m, and findFlippedNeighbors.m. The simulation process is outlined within the main code text and in the Computer Simulation subsection of the Materials and methods. The code was adapted from Ivanovic et al (2013) to include a possibility of Nh=6 and the unproductive HA population, and to measure hemifusion delay from the start of the simulation rather than from the arrest intermediate.
- https://doi.org/10.7554/eLife.11009.025
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Distinct functional determinants of influenza hemagglutinin-mediated membrane fusion
eLife 4:e11009.
https://doi.org/10.7554/eLife.11009
