Integrative neuromechanics of crawling in D. melanogaster larvae
- Harvard University, United States
- Simons Foundation, United States
- The University of Liverpool, United Kingdom
Figures
Figure 1
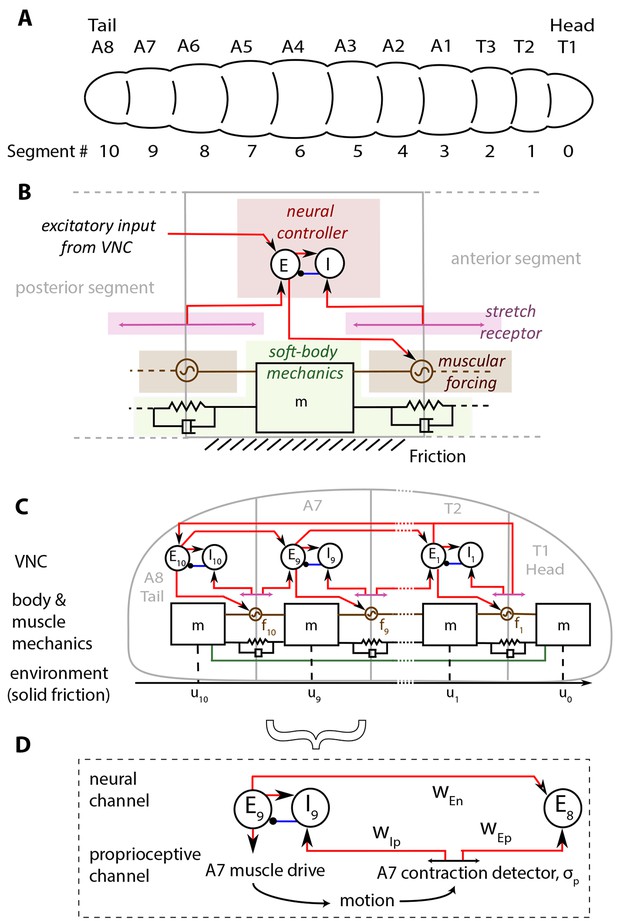
Schematic of the model.
(A) Drosophila larvae have segmented bodies. (B) An overview of the model for one segment. Only input neural and proprioceptive signals are shown to the neural controller, its output is not shown. Shades mark subsystems. Red lines show excitatory neural synapses, blue denotes inhibitory synapses. (C) The larva body is modeled as a linear chain of masses, connected by damped linear springs. Head and tail segments are coupled mechanically, denoted by the green line. Each segment feels friction due to contact with the substrate. Body segments are actuated with muscular forces, , that are excited by input from the larva VNC. VNC is modeled as a chain of excitatory, , and inhibitory, , neural populations. Self-coupling of populations are not shown. VNC gets proprioceptive input that signals contraction of a particular segment, shown by lines with arrows on both ends. (D) Segment-to-segment propagation of neural activity happens through neural () and proprioceptive () couplings. Detailed description and model equations are given in the Model section.
Figure 2
Sustained crawling.
Time is in units of . Model is simulated for , only first is shown. All simulations were based on Equations (1–5), with parameter values as specified in the Table 1. Shade shows the duration of an example peristaltic wave. (A) Kymograph of body segments. Distance is measured in units of . (B) Muscular forces in segments. Same color code is used as in the A). (C) Neural activity in segments. Solid line denotes excitatory neuron population activity, and dashed lines denote inhibitory population. Same color code is used as in the A)
Figure 3
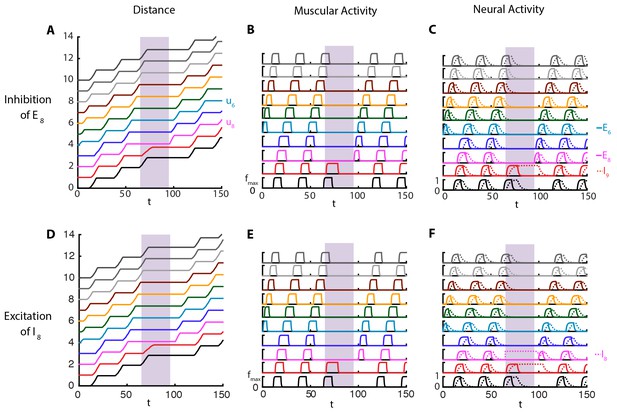
Perturbations of VNC.
Top row: is inhibited for , shown in purple. Bottom row: is maximally excited in the range , shown in purple. Color code and parameters are the same as Figure 1. (A) and (D) Kymograph of body segments. (B) and (E) Muscular forces in segments. (C) and (F) Neural activity in segments. We note that in these simulations, crawling is started at with an excitatory pulse applied to of the stationary larva, demonstrating that our model allows for the peristaltic wave to start at any segment.
Figure 4
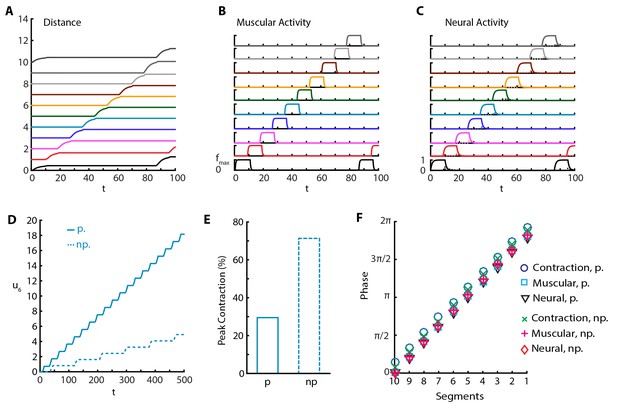
Sustained crawling without proprioception.
The absence of proprioception induces slower crawling. In the lower panels, “p.” denotes crawling with proprioception, 'np.' denotes crawling without proprioception. (A) Kymograph of body segments. (B) Muscular forces in segments. (C) Neural activity in segments. (D) Kymograph of A4 segment () in the full model vs. the model without proprioceptive feedback. (E) Peak contraction of A3-A4 () segmental distance averaged over waves. Here, we plot only one segment interval as in (Hughes and Thomas, 2007) to ease comparison. (F) Phases of (excitatory) neural, muscular and contraction activity in different segments within a wave, with respect to excitatory neuron activity in tail segment. To calculate phases, first Discrete Fourier Transform of the relevant signal is obtained. Phase is the negative complex phase of the fundamental frequency. Contraction of a segment is the difference between its and next anterior neighbor segment’s center of mass displacements.
Figure 5
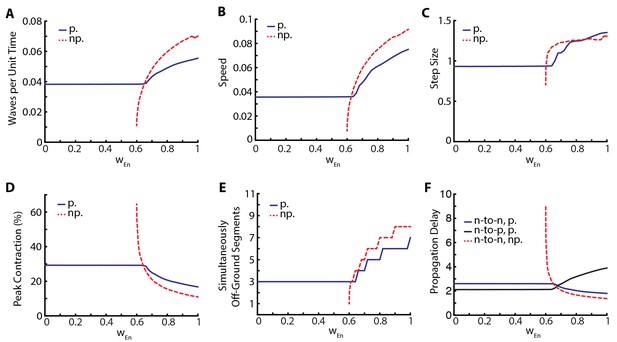
Proprioception increases robustness of crawling.
Crawling metrics as a function of . In dashed-red, we show the results from the model without proprioceptive feedback (np.), while in blue and black, we show the results with proprioception (p.) based on Equation (1–5) with parameter values as described in the Table 1. (A) Peristaltic waves per unit time (). (B) Speed of crawling in units of . (C) Step size, defined as the tail displacement divided by number of waves. It is measured in units of (L) D) Peak contraction in a segment, averaged over segments and waves. E) Number of simultaneously off-ground segments. This number is calculated at each time step, and the median number across time steps are plotted. (F) Propagation delays through neural and proprioceptive channels (see text for a detailed discussion) are shown. 'n-to-n' denotes neuron propagation delay. 'n-to-p' denotes proprioceptive propagation delay.
Figure 6
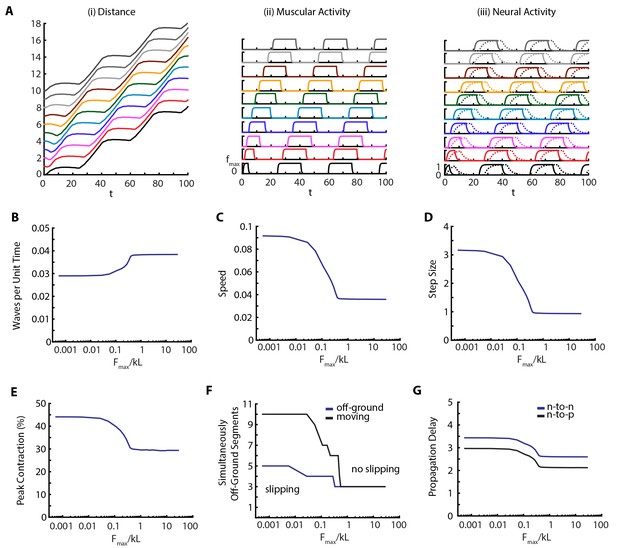
Decreasing friction leads to slippage.
(A) Kymograph, muscular forces and neural activity as a function of time for . See Figure 2 and text for explanation of plots. (B,C,D,E) Crawling metrics as a function of . See Figure 5 and text for explanation of plots.
Appendix 1—figure 1
Crawling in a model with only head-tail neural coupling.
(A) Schematic of modified model. (B) Perfectly synchronous driving of and . A full kymograph, muscular activity and neural activity. Below the kymograph, the changes in total length of the larva is shown. Color code is the same as Figure 1. (C) Delayed forcing of tail by 0.2 radians. Same figures as B).
Appendix 2—figure 1
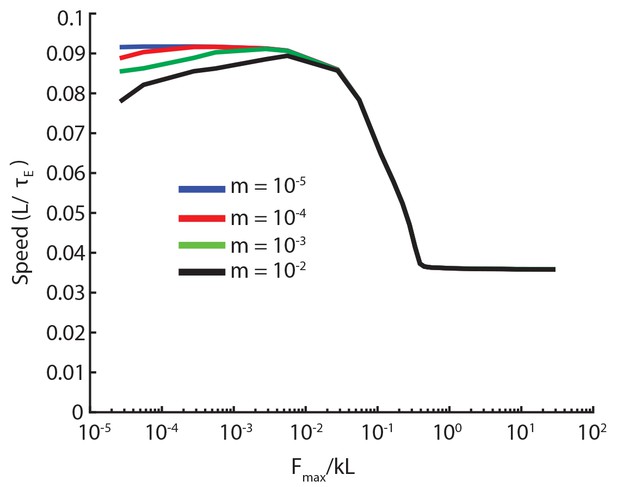
Speed vs. friction force for different values of inertia.
https://doi.org/10.7554/eLife.11031.016Videos
Video 1
GFP imaging of Drosophila larva forward crawling body segment and gut movements.
Courtesy of Ellie Heckscher. See also reference (Heckscher et al., 2012). Original video is available at: https://www.youtube.com/watch?v=1d7zMYWLjLI
Video 2
Crawling simulations of full model larva.
To illustrate the changes in friction, body segments are drawn off the ground when exceeds in Equation (5).
Video 3
Crawling simulations of full model larva.
Cycle is started at A4 and temporarily stopped at A6 by inhibiting the excitatory population.
Video 4
Crawling simulations of full model larva.
Cycle is started at A4 and temporarily stopped at A6 by exciting the inhibitory population.
Video 5
Crawling simulations of larva with silenced proprioception.
https://doi.org/10.7554/eLife.11031.011
Video 6
Crawling simulations of larva with low friction.
https://doi.org/10.7554/eLife.11031.014Tables
Table 1
Dimensionless parameters of our model and their default values used in numerical simulations.
| 3.5 | 5/6 | 0.4 | |||
| 25/3 | 5/12 | 3 | |||
| 1 | -2 | 0.6 | |||
| 0 | 0.6 | 1.95 | |||
| 1.95 | 0.4 | 0.6 | |||
| -17/18 | 40000 | 1000 |
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Integrative neuromechanics of crawling in D. melanogaster larvae
eLife 5:e11031.
https://doi.org/10.7554/eLife.11031
