Neural evidence accumulation persists after choice to inform metacognitive judgments
- Trinity College Dublin, Ireland
- Leiden University, The Netherlands
Figures
Figure 1 with 1 supplement
Go/No-Go task and associated behavior.
(a) Subjects’ primary task was to make a speeded manual response (‘A’) to all incongruent color/word stimuli and to withhold from responding to congruent stimuli or when the same word was presented on consecutive trials. Following any commission errors, they were instructed to signal error detection as quickly as possible by pressing a secondary response button (‘B’). (b) Distribution of trial types averaged across subjects. C = correct withhold, E = error, D = detected error, U = undetected error. Error bars = s.e.m. (c) Histograms representing stimulus onset and detection response time (RTd) distributions on detected error trials, aligned to error commission and pooled across all subjects.
Figure 1—figure supplement 1
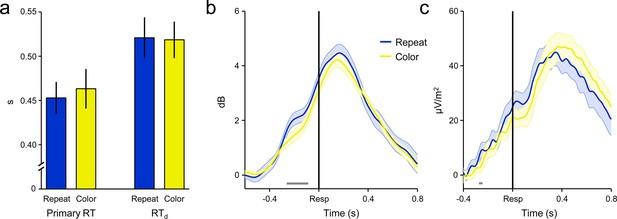
‘Repeat’ and ‘color’ No-Go stimuli did not differentially affect primary RT, RTd or decision signal morphology on detected error trials.
(a) Group-averaged median primary RT (left) and RTd (right) for detected errors to repeat and color No-Go stimuli. There was no effect of stimulus-type on either metric (both p > 0.3). (b) FCθ power aligned to the primary response on detected error trials, separately for both No-Go stimulus-types. (c) Detected-error CPP waveforms aligned to the primary response for both No-Go stimulus-types. Only subjects with ≥8 trials per stimulus-type were included in b and c (n = 24). Gray running markers at bottom indicate significant stimulus-type effect (p < 0.05, paired t-test for repeat vs color). Error bars and shaded error regions = s.e.m.
Figure 2 with 2 supplements
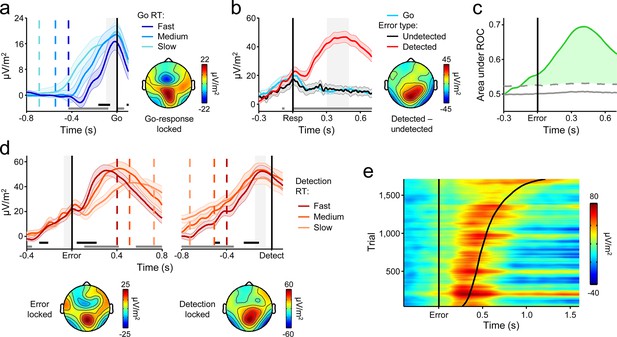
A centro-parietal decision signal for first- and second-order decision-making.
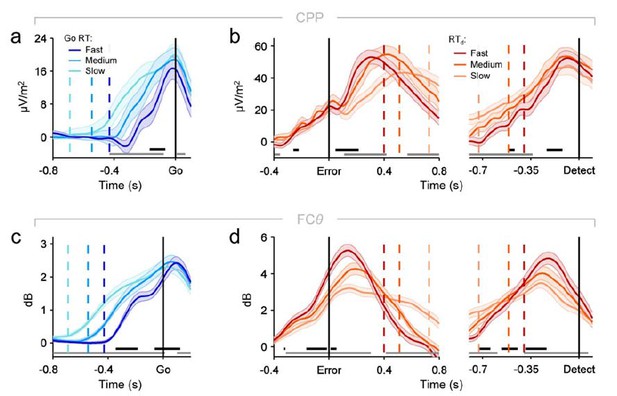
(a) Go-trial CPP waveforms aligned to primary task response and sorted by RT into three equal-sized bins, and associated scalp topography. (b) CPPs again aligned to primary response, but separately for Go trials and detected and undetected errors; gray running marker indicates significant detection effect (p < 0.05, paired t-test for detected vs. undetected). Topography illustrates scalp distribution of error detection effect. (c) Time-course of detection-predictive activity estimated as the area under the ROC curve. Permutation mean and significance threshold (1.96 s.d.) are marked as solid and dashed gray lines, respectively. (d) Detected-error CPP, aligned to primary task response and subsequent error detection report; waveforms were sorted and binned by RTd. (e) Single-trial surface plot showing temporal relationship between the CPP and RTd (curved black line); waveforms were pooled across subjects, sorted by RTd and smoothed over bins of 50 trials with Gaussian-weighted moving average. Vertical dashed lines in a and d represent median RTs. Gray markers at bottom of these plots indicate time points when linear regression of RT on signal amplitude reached significance (p < 0.05); black markers indicate center of 150 ms time windows in which regression of RT on signal slope reached significance (p < 0.05; one-tailed predicting steeper slope for faster RTs). Shaded gray areas show latencies of all associated scalp topographies. All traces were baselined to pre-stimulus period. Shaded error bars = s.e.m.
Figure 2—figure supplement 1
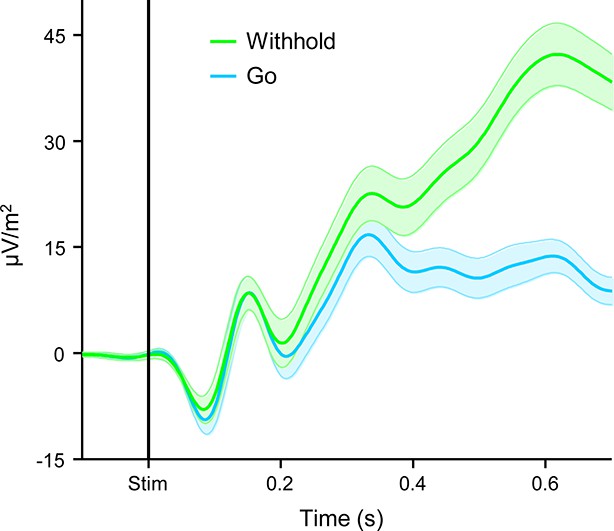
The CPP aligned to stimulus onset, separately for Go and correctly withheld No-Go trials.
The plot illustrates that the first-order CPP traces the emerging decision regardless of its outcome. The delayed peak latency and large amplitude of the CPP on correct withhold trials (green) are consistent with the biased decision-making context created by our task design: No-Go trials were rare relative to Go trials (ratio of approximately 1:8) which, in models of bounded evidence accumulation, manifests in slower decision times and a greater distance-to-threshold for committing to a No-Go decision. Shaded error regions = s.e.m.
Figure 2—figure supplement 2
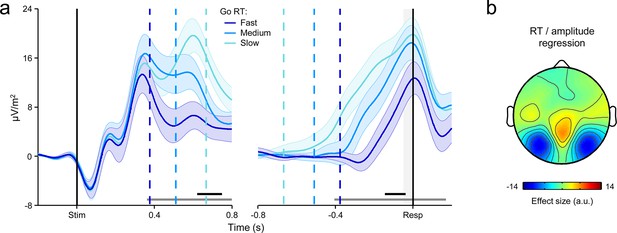
Early stimulus-evoked deflections affect first-order CPP amplitude on fast Go trials.
(a) Grand-average stimulus- (left) and response-aligned (right) CPPs derived from all Go trials and sorted per-subject by primary RT into three equal-sized bins. Vertical dashed lines show median RTs per bin. Gray markers at bottom indicate time points at which a linear regression of RT on signal amplitude reached significance (p < 0.05); black markers indicate the center of 150 ms time windows in which a regression of RT on signal slope reached significance (p < 0.05; one-tailed based on prediction of steeper slope for faster RTs). First-order CPP amplitude appeared to increase as a function of RT in the response-aligned waveforms. Shaded error bars = s.e.m. (b) Scalp map showing the topographic distribution of the single-trial relationship between response-aligned signal amplitude (latency of measurement indicated by shaded gray region in a, right) and primary RT on Go trials (within-subjects robust regressions; effect size = regression coefficient/s.e.m.). The distribution of the RT/amplitude effect was very similar to that observed for visual-evoked potentials, thus suggesting contamination of decision signals on fast trials by these early deflections and motivating our exclusion of Go trials with RT <350 ms from analyses reported in the main manuscript.
Figure 3 with 3 supplements
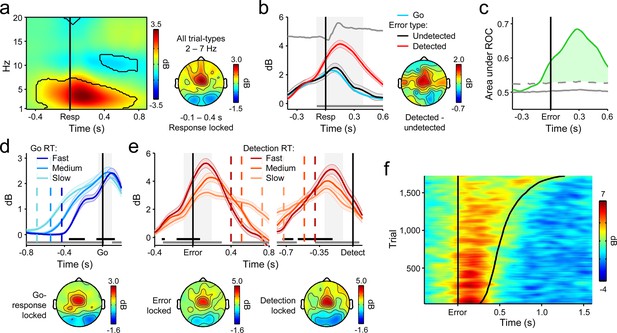
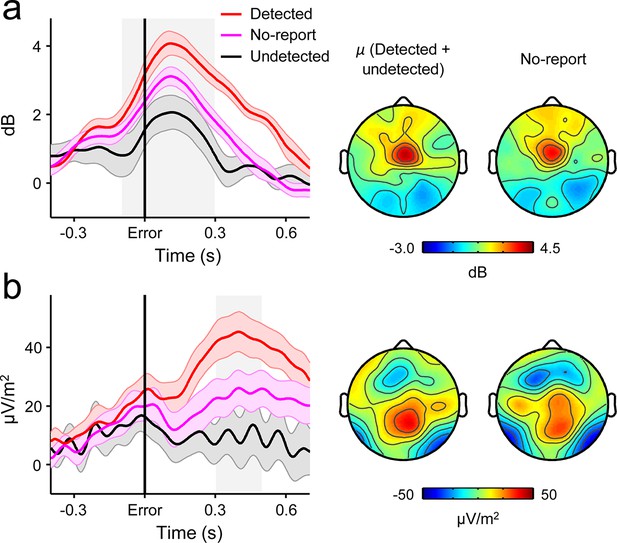
Fronto-central θ-band (2–7 Hz) oscillatory power predicts the accuracy and timing of error detection reports.
(a) Time-frequency plot of fronto-central power, aligned to the primary task response and averaged across detected error, undetected error and RT-matched go trials; black lines enclose regions of significant power change relative to a pre-stimulus baseline (p < 0.01, paired t-test). Scalp topography shows θ power averaged over all trial types. (b) Response-aligned FCθ waveforms separately for each trial type; gray trace is the condition-averaged ERP (arbitrarily scaled). Topography illustrates scalp distribution of error detection effect. (c) Time-course of FCθ detection-predictive activity quantified by the area under the ROC curve. (d) Go-trial FCθ waveforms and associated scalp topography, aligned to primary task response; single-trial waveforms were sorted by primary RT and divided three equal-sized bins. (e) Detected-error FCθ waveforms and topographies, aligned to both the primary task response (left) and the subsequent error detection report (right); waveforms were sorted and binned by RTd. (f) Single-trial surface plot showing the temporal relationship between the FCθ power and RTd (curved black line). Conventions for b–f are the same as in Figure 2. All traces were again baselined to the pre-stimulus period. Plots in a were calculated via wavelet convolution; all other plots show filter-Hilbert transformed data (see Materials and methods).
Figure 3—figure supplement 1
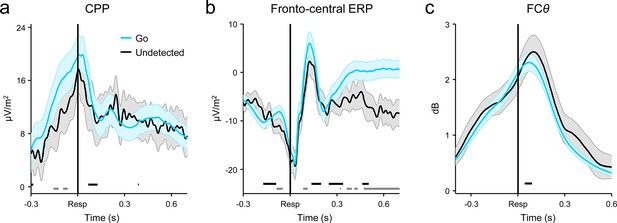
Comparison of response-aligned CPP (a), fronto-central ERP (b) and FCθ (c) signals on correct Go trials and undetected errors.
Fronto-central ERPs were averaged over electrodes FCz, F1 and F2 (see also Figure 3—figure supplement 2). Gray running markers at bottom indicate latencies of significant amplitude differences, while black markers indicate center of 150ms time windows within which signal slope differed between trial-types (both comparisons were paired t-tests, p < 0.05, two-tailed). Shaded error regions = s.e.m.
Figure 3—figure supplement 2
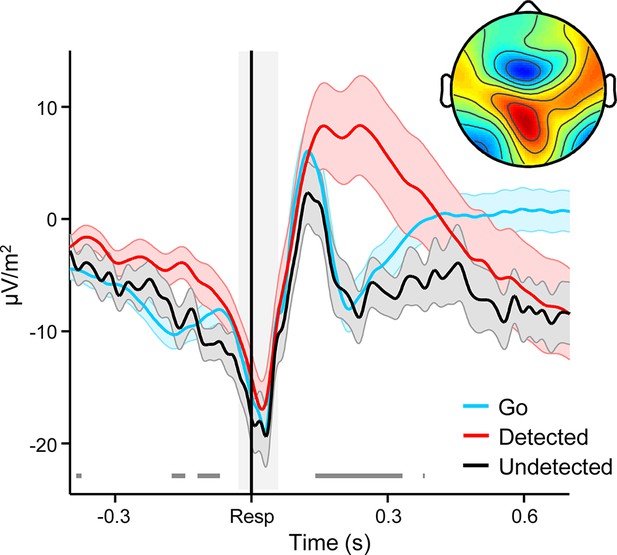
Broadband ERPs averaged over fronto-central electrodes FCz, F1 and F2 and aligned to the primary response, separately for Go trials and detected and undetected errors.
The prominent peri-response negativity corresponds to the error-related negativity (ERN) component. Shaded gray area shows latency of associated scalp topography, collapsed across trial-types (inset). Selected channels for ERN analysis accorded with the topographic location of the fronto-central minimum. Gray running markers at bottom indicate latencies of significant error detection effects (p < 0.05, paired t-test for detected vs undetected errors). Shaded error regions = s.e.m.
Figure 3—figure supplement 3
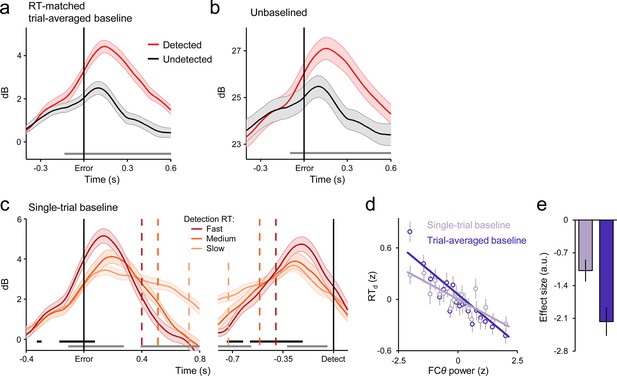
Robustness of the FCθ effects to primary RT differences and baselining regimes.
(a) Error-aligned FCθ waveforms for detected and undetected errors using subsets of trials that were matched for primary RT; persistent of error detection effect indicates robustness to condition-related differences in RT. (b) Error-aligned FCθ waveforms without application of any baseline; combined with Figure 3b of the main manuscript, indicates robustness of error detection effect to different baselining regimes. (c) Detected-error FCθ waveforms baselined at the single-trial level, and aligned to both error commission (left) and subsequent error detection report (right) after sorting and binning by RTd. Compare to Figure 3e of main manuscript. (d) Scatterplot illustrating the linear relationship between FCθ power and RTd when trial-by-trial variation in baseline power is either intact (darker purple) or removed (lighter purple); data were z-scored within subjects, pooled across subjects and grouped into 20 five-percentile bins. (e) Estimated effect sizes from within-subjects robust regressions of RTd on FCθ using both baselining regimes depicted in d; effect was qualitatively weaker when variation in baseline power was eliminated. Shaded regions in a-c and vertical lines in d and e = s.e.m. Gray running markers at bottom of a-c indicate latencies of significant error detection effects (p < 0.05, paired t-test for detected vs undetected errors) in a and b and latencies of at which a linear regression of RTd on signal amplitude reached significance (p < 0.05) in c. Black markers in c indicate center of 150ms time windows in which regression of RTd on signal slope reached significance (p < 0.05; one-tailed predicting steeper slope for faster RTs).
Figure 4 with 1 supplement
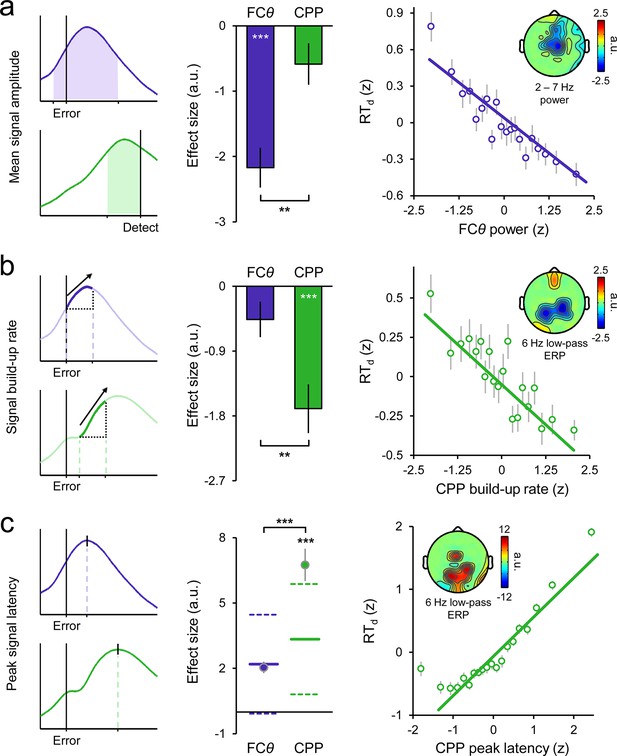
Variance in the timing of error detection reports is explained by distinct single-trial metrics of FCθ and CPP morphology.
(a) Schematic depicting the single-trial measurement windows for FCθ power (purple) and CPP amplitude (green; left). Bar graphs (middle) show estimated effect sizes from within-subjects robust multiple regressions of RTd on both amplitude metrics (error bars = s.e.m.), and the associated topography (inset right) indicates the scalp distribution of the theta power effect. Scatterplot (right) illustrates the linear relationship between FCθ power and RTd; points and error bars are mean ± s.e.m. of data that were z-scored within subjects, pooled across subjects and grouped into 20 five-percentile bins. (b) Measurement approach, regression-estimated effect sizes, topographic distribution and scatterplot representing the single-trial relationships between RTd and signal build-up rates. (c) Similar plots representing the relationships between RTd and peak signal latencies. Points in the effect size plot (middle) indicate observed effect sizes, solid and dashed lines highlight the mean and 95% confidence intervals, respectively, of permuted distributions used for significance testing (see Materials and methods). Topographies are thresholded at p < 0.005 (a, b) and p < 0.0001 (c) for effect visualization. The solid lines in all scatterplots are simple linear robust regression fits to the unbinned data. **p < 0.01; ***p < 0.001.
Figure 4—figure supplement 1
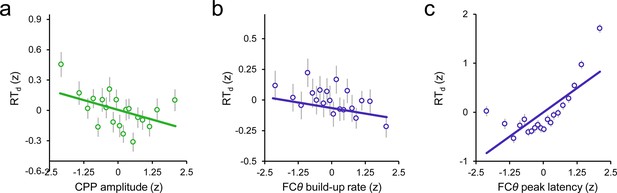
Scatterplots illustrating the linear relationships between RTd and second-order CPP amplitude (a), FCθ build-up rate (b) and FCθ peak latency (c).
Points and error bars are mean ± s.e.m. of data that were z-scored within subjects, pooled across subjects and grouped into 20 five-percentile bins. Solid lines are simple linear robust regression fits to the unbinned data.
Figure 5 with 1 supplement
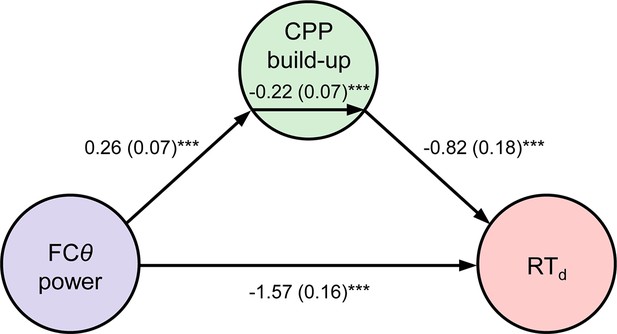
Mediation analysis.
Path diagram depicts the relationships between nodes in a mediation model that tested whether CPP build-up rate mediated the negative relationship between FCθ power and RTd. Lines are labeled with path coefficients, with s.e.m. shown in parentheses. FCθ power (predictor, left) predicted CPP build-up rate (mediator, middle), which in turn predicted RTd (outcome, right) controlling for FCθ power. The upper-middle coefficient indicates the formal mediation effect. The significant direct path between FCθ power and RTd, calculated controlling for the mediator, indicates partial mediation: CPP build-up rate did not explain all of the shared variance between FCθ and RTd. ***p < 0.001, bootstrapped.
Figure 5—figure supplement 1
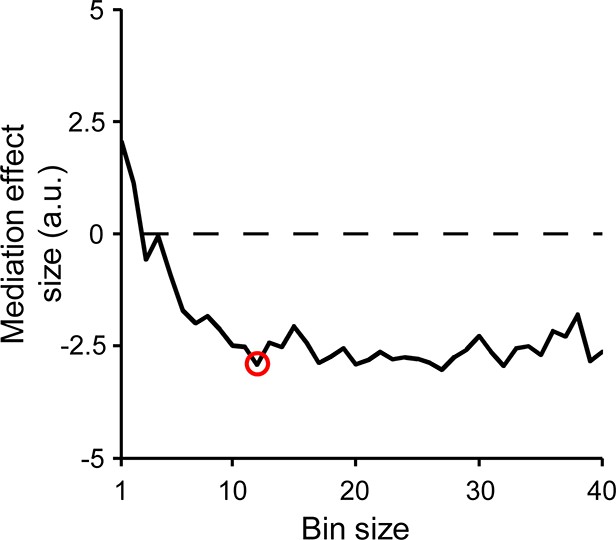
Effects of trial binning on CPP build-up rate mediation effect.
Plot depicts effect size (mediation coefficient/s.e.m.) of the mediation of the relationship between FCθ and RTd by second-order CPP build-up rate, across a range of bin sizes. The strength of the effect strongly increased as bin size increased initially, indicating the desired enhancement in signal-to-noise by trial binning. Red marker indicates bin size used for the analysis depicted in Figure 5 of the main manuscript.
Figure 6 with 2 supplements
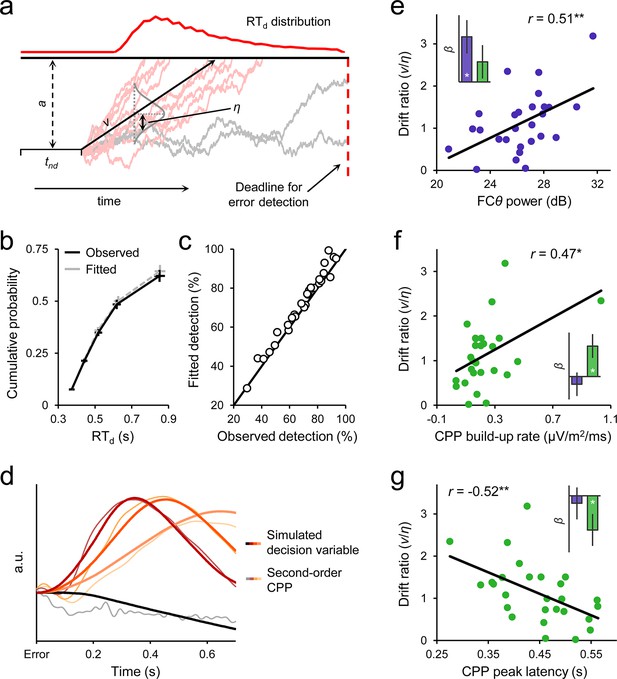
Diffusion modelling of error detection behavior.
(a) Schematic representation of the one-choice drift diffusion model. Noisy error evidence accumulates over time at mean drift rate v until a threshold a is reached (light red traces) or a deadline on detection expires (gray traces). Drift rate is normally distributed across trials with standard deviation η, and non-decision-related processing time is captured by tnd. Within-trial noise s is fixed at 0.1 (not shown). (b) Group-level model fit. Points from left to right represent the 0.1, 0.3, 0.5, 0.7 and 0.9 RTd quantiles, estimated from the data (black) and generated by the model fit (gray). (c) Observed versus fitted error detection accuracy. Diagonal line is the identity line. (d) Group-average decision variables reflecting the accumulation of error evidence, simulated using the best-fitting model parameters for each subject and overlaid on the grand-average second-order CPP signals. Detected error traces are sorted by RTd into three equal-sized bins. CPPs are baselined to the 50 ms preceding error. (e) Between-subjects relationship between FCθ power and model-estimated drift ratio (v/η). Bar graph (inset) shows standardized regression coefficients from a multiple regression that included CPP amplitude as an additional predictor. (f, g) Scatterplots and bar graphs highlighting between-subjects relationships between drift ratio and signal build-up rates (f) and peak latencies (g). Although one extreme data point is apparent in f, this did not exert disproportionate influence over the fitted regression line (studentized deleted residual < 1) and the correlation remained marginally significant when it was removed (r = 0.37, p = 0.06). Error bars = s.e.m. *p < 0.05; **p < 0.01.
Figure 6—figure supplement 1
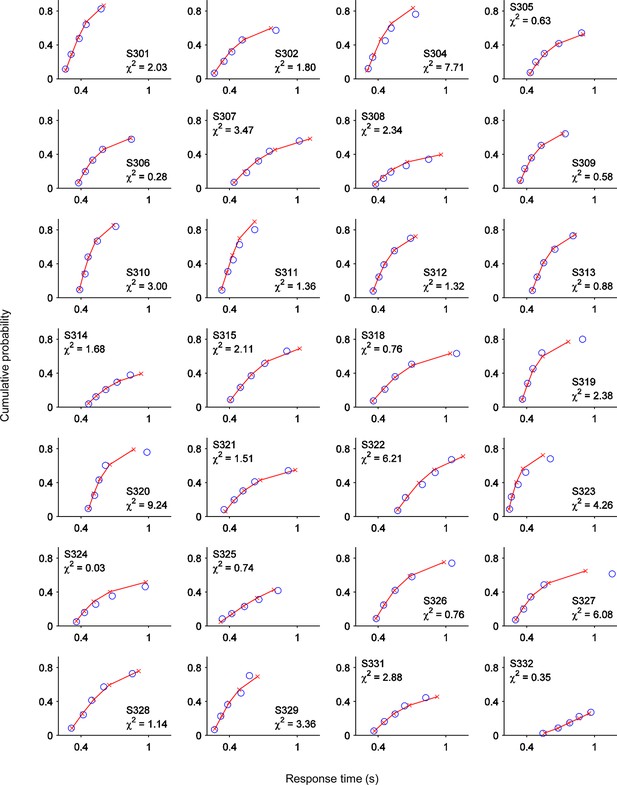
One-choice diffusion model fits for single subjects.
Points from left to right represent the 0.1, 0.3, 0.5, 0.7 and 0.9 RTd quantiles, estimated from the data (red lines and crosses) and predicted by the model (blue circles). Text at inset of each plot indicates subject number and χ2 error term for that subject.
Figure 6—figure supplement 2
Between-subjects relationship between FCθ power and model-estimated drift ratio (v/η) when a trial-averaged baseline was applied to FCθ.
Compare to Figure 6e of main manuscript.
Figure 7
Second-order decision signals persist in the absence of error reporting demands.
(a) Time-courses and topographic distributions of FCθ power from a new cohort that performed half of task blocks without any explicit instruction to self-monitor performance (‘no-report’ blocks). Left topography is the average topographic distribution of θ-power after pooling all detected and undetected error trials from blocks with self-initiated error detection reporting; right topography is θ distribution averaged across all errors in no-report blocks. (b) Time-courses and topographies of the second-order CPP component from the same cohort. Conventions are the same as in (a). Shaded gray areas in left show latencies of associated scalp topographies. Shaded error bars = s.e.m.
Author response image 1
Re-plotting of panels from figures 2A, 2D, 3D and 3E from the main manuscript, using two-tailed rather than one-tailed tests on signal build-up rates (significance indicated by black running markers).
https://doi.org/10.7554/eLife.11946.021Tables
Table 1
Parameter estimates and goodness-of-fit of error detection diffusion model.
| a | tnd | v | η | χ2 | |
|---|---|---|---|---|---|
| Mean | 0.21 | 0.20 | 0.45 | 0.45 | 2.46 |
| s.d. | 0.12 | 0.08 | 0.30 | 0.30 | 2.33 |
-
χ2 degrees of freedom = 1, critical value = 5.024.
-
24 of 28 χ2 values were below the critical value.
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Neural evidence accumulation persists after choice to inform metacognitive judgments
eLife 4:e11946.
https://doi.org/10.7554/eLife.11946
