RETRACTED: A mathematical model explains saturating axon guidance responses to molecular gradients

Abstract
eLife digest
Introduction
Results
Discussion
Materials and methods
References
Article and author information
Metrics

Abstract

Correct wiring is crucial for the proper functioning of the nervous system. Molecular gradients provide critical signals to guide growth cones, which are the motile tips of developing axons, to their targets. However, in vitro, growth cones trace highly stochastic trajectories, and exactly how molecular gradients bias their movement is unclear. Here, we introduce a mathematical model based on persistence, bias, and noise to describe this behaviour, constrained directly by measurements of the detailed statistics of growth cone movements in both attractive and repulsive gradients in a microfluidic device. This model provides a mathematical explanation for why average axon turning angles in gradients in vitro saturate very rapidly with time at relatively small values. This work introduces the most accurate predictive model of growth cone trajectories to date, and deepens our understanding of axon guidance events both in vitro and in vivo.

https://doi.org/10.7554/eLife.12248.001

eLife digest

For your brain to work, millions of nerve cells have to be connected together precisely. To achieve this, growing nerve fibres navigate through the developing brain by following chemical cues. One important such cue is how the concentration of a chemical varies with distance across the brain. This variation is known as a chemical gradient. However we still don't fully understand exactly how nerve fibres use such gradients to steer themselves.

Nguyen et al. have built a mathematical model that accounts for the way that nerve fibres respond to chemical gradients, and showed that the model closely matched new experimental data on the growth of nerve fibres from the rat brain. The model implies that, under some conditions, nerve fibres turn surprisingly little in response to a chemical gradient.

Nguyen et al.’s model can now be used to predict nerve fibre responses in many other situations, and could help researchers to understand more about how the brain becomes wired up during development. The model could also reveal more about the conditions that are needed to cause nerve fibres to turn sharply in response to chemical gradients.

https://doi.org/10.7554/eLife.12248.002

Introduction

For the brain to function correctly, it must be wired correctly. Indeed, many neurodevelopmental disorders are likely the result of wiring defects (Yaron and Zheng, 2007; Geschwind and Levitt, 2007; Lin et al., 2009; Stoeckli, 2012). Axon guidance, where axons grow and navigate to their targets, occurs primarily via the sensing of molecular cues in the environment. A critical mechanism by which such cues act is believed to be concentration gradients, causing axons to be attracted or repelled in particular directions (Mortimer et al., 2008; Lowery and Van Vactor, 2009). However, despite major advances in understanding which molecules are involved in this process (Tessier-Lavigne and Goodman, 1996; Dickson, 2002; Chilton, 2006; Kolodkin and Tessier-Lavigne, 2011), an accurate quantitative model describing how axon trajectories are influenced by such guidance cues is still lacking.

In vivo, axon trajectories may potentially be influenced by many cues. In vitro assays allow individual influences, such as that from the concentration gradient of a single guidance factor, to be isolated and quantified. A substantial mystery posed by in vitro axonal chemotaxis assays is the relatively weak turning produced, even over long periods of time. The naive prediction that axons would promptly turn until they become fully aligned with the gradient turns out not to be true. In an early study of chemotactic responses of chick sensory neurons to a gradient of nerve growth factor in a diffusion chamber, only 60% of nerve tips were preferentially directed toward the gradient direction after 46 hr of growth (Letourneau, 1978). The growth cone turning assay over 1–2 hr produces average turning angles typically ranging from 10 to 25°, with high variability (Song et al., 1997; Höpker et al., 1999; Xiang et al., 2002; Ming et al., 2002; Thompson et al., 2011). A similarly weak response is observed in the Dunn chamber (Kent et al., 2010; Dudanova et al., 2012; Ruiz de Almodovar et al., 2011; Dudanova et al., 2010; Yam et al., 2009). More recent studies using microfluidic technologies over timescales ranging from hours to days have also elicited average axon turning angles only up to 10–15° (Wang et al., 2008; Morel et al., 2012; Taylor et al., 2015; Sloan et al., 2015). Why average turning angles are so small, and what this means for axon guidance in vivo, are unclear.

One of the key properties of in vitro axon growth that might explain this mystery is that it is often very straight (Katz et al., 1984; Katz, 1985). Axons are under mechanical tension from the pull of the growth cone (Bray, 1973; Bray, 1979), and this tension stimulates the elongation of the axon by stretching (Bray, 1984; Zheng et al., 1991). Traction forces generated in the growth cone arise from the coupling of the continuous retrograde flow of actin to the substrate through adhesion receptors (Franze and Guck, 2010; Betz et al., 2011; Athamneh and Suter, 2015). For reasons which are not clear, axons tend not to bend and follow the highly random movements of their growth cones. Rather, they usually form a straight line between their tip and a location where they are firmly attached to the substrate (i.e. a focal adhesion (Kaverina et al., 2002)). We call such locations anchor points; they can be at the soma, at a branch point, or at some other seemingly sporadic location along the axon. Although it is not clear how this tension leads to elongation, the growth cone advances largely in the stretch direction along the axon, resulting in relatively straight paths.

To determine quantitatively what effect this might have on axonal trajectories requires mathematical modelling. Growth cone movements were first analyzed in detail in (Katz et al., 1984; Katz, 1985). Subsequently, various phenomenological models have been built that differ as to how they treat stochasticity, and mechanisms for directional preference, namely turning or growth rate modulation. One set attempted to fit the dynamics of growth cone movement to a random walk with drift (Buettner et al., 1994; Odde and Buettner, 1995; Maskery et al., 2004; Pearson et al., 2011). Li et al. simulated trajectories by assuming the turning angle of the growth cone is in proportion to the angle between the neurite and the resultant filopodial tension (Li et al., 1995). In (Borisyuk et al., 2008), the axon growth angle depends on the tendency to turn toward the gradient angle and noise. The noise term is small (2–5°), leading to straight paths that resemble axon growth in the tadpole spinal cord. Another set of models has concentrated on how asymmetric receptor binding across the growth cone might be used as the basis of a turning signal (Goodhill et al., 2004; Xu et al., 2005; Mortimer et al., 2010), but without considering the consequence for whole trajectories. A third group of models considers the possibility that the velocity of the growth cone is influenced by an attractive gradient from the target cells, and chemoattractants and chemorepellants released from other growth cones and itself (Hentschel and Ooyen, 1999; Krottje and van Ooyen, 2007). However, none of these models has been closely compared with the details of experimentally measured trajectories in gradients, and parameters such as variability in step sizes, the distribution of instantaneous turning angles, and straightness of real paths, have not been addressed. Thus, the question of whether there is a model that can adequately capture all these characteristics of real trajectories remains open. Without such a model, it is difficult to determine if trajectories observed in vivo are in fact consistent with gradient guidance.

Here, we present a new computational model for axonal trajectories based on the combined influence of anchor points, a tendency to turn toward the gradient direction, and random noise. We found experimentally that the gradient had no effect on the step sizes; thus, we only model the turning angles. Critically, the model predicts rapid near saturation of average turning angles with time. To test this model quantitatively, we then introduce a new microfluidics assay for studying axonal response to gradients, and using timelapse imaging characterize the behavior of axons over several hours of growth in both attractive and repulsive gradients. We find that our model fits the behavior observed very closely. We then investigate by simulation the effect of increasing the number of anchor points, and find that this increases the average fidelity of turning but at the cost of higher variability. Together, this work both explains why turning response to gradient saturates so rapidly and reveals the quantitative principles that are required to reproduce accurately in vitro axonal trajectories in response to chemotactic gradients. The model identifies straightness as a limiting factor on how much axons can turn and suggests that the frequency of anchor points plays a key role in the axonal turning response to a gradient.

Results

A mathematical model of growth cone trajectories

We modelled three basic influences on the direction of axon growth: a tendency to grow straight, the effect of a chemotactic gradient, if present, and random movement noise. In a fixed coordinate system with arbitrary zero angle direction, we define θ(t) as the bearing of the growth cone at time step $t$ , ϕ( $t$ ) as the angle of the vector connecting the growth cone to its anchor point, and Ψ as the gradient direction (terminology is summarized in Table 1). We define ‘bearing change’ as Δθ( $t$ ), the change in θ(t) at time step $t$ , distinct from ‘turning angle’ ψ_turn, the total change in θ from the initial direction of growth over long periods of time. For simulations we identify each timestep as 5 min of real time. The model (Figure 1) is then

Table 1

Summary of model parameters (GC: growth cone).

https://doi.org/10.7554/eLife.12248.003

Symbol	Meaning
$θ$	GC’s current bearing
$Φ$	GC’s overall angle
$Ψ$	Gradient direction
$Δ θ$	Bearing change
$ψ_{t u r n}$	Turning angle after 80 min
$a$	Persistence strength
$b$	Bias strength
$ξ$	Noise in bearing change
$σ$	Standard deviation of $ξ$
$s$	Step size every 5 min
$L$	Distance from origin to GC
$S$	Straightness index
$r$	Anchoring rate

Figure 1

Download asset Open asset

Model set-up and the noiseless case.

(A) The axon starts growing from the soma (black segment) at initiation angle ϕ(0). At each time point, the bearing is *θ(t),* and the bearing change between t and t + 1 is Δθ( $t$ ). ϕ( $t$ ) is the angle of the vector connecting the current position of the growth cone with the anchor point. Ψ is the fixed gradient direction. (B) The turning angle ψ*_turn* at time $t$ is the angle between the initial direction of growth, and the line joining the initial and current positions of the growth cone. (C) Simulation of the growth cone angle using Equation (1) in the noiseless case (ξ = 0) with the same $a$ = 1 and different values of b. The dashed line is the power law $ϕ (t) \propto t^{\frac{- b}{a + b}}$ . In the long time limit, this law accurately describes the angle of the growth cone. (D) Simulations of the trajectories for different combinations of $a$ and $b$ in the absence of noise. Larger $b$ leads to stronger turning. When $a$ = 0, the growth cone very rapidly aligns with the gradient. The persistence term ( $t$ > 0) leads to incomplete turning.

https://doi.org/10.7554/eLife.12248.004

Figure 1—source code 1 The code to simulate the trajectories based on Equation 1 in the noiseless case.: https://doi.org/10.7554/eLife.12248.005
Download elife-12248-fig1-code1-v2.zip

∆ θ (t) = a ∠ (ϕ (t), θ (t)) + b ∠ (Ψ, θ (t)) + ξ

where $a$ scales persistence to move in the same direction as the overall direction of the axon, $b$ scales the bias due to the gradient, and ξ is random noise in the bearing changes. The symbol ∠( $x, y$ ) denotes the signed angle between the unit vectors with angles $x$ and $y$ , and constrains the resultant angle to be between −π and π. The step size is the distance moved after one time step and will later be estimated empirically.

We consider first the noiseless case (ξ = 0) in long- and finite-time regimes, and then consider the effects of noise. Figure 1C shows the results of setting ξ = 0, with a fixed step size of $s$ = 3 μm, and simulating the model for long times with the same $a$ = 1 and different values of $b$ (0.1, 0.2 and 0.3). Turning angles rapidly saturate, which can be understood analytically (see 'Materials and methods'): in the $t \to \infty$ limit, the growth cone angle follows a power law with respect to time $ϕ (t) \propto t^{(α - 1)}$ or $\log (ϕ (t)) = c o n s t + (α - 1) \log (t)$ (where $α = a / (a + b)$ ) (Figure 1C). This relationship generally holds for $t > \exp (4) \approx 4$ h, meaning that for long times, the rate of change of angle decreases and this rate is determined by the power law exponent $b$ /( $a$ + $b$ ). Since comparison with empirical data (see later) shows that the biologically relevant regime is $b$ ≪ $a$ , the exponent is generally small. Thus, while ultimately axons in the model do eventually align with the gradient, this process takes an exceedingly long time. This explains the slow and decreasing change in the turning angle over time in the noiseless case.

The finite $t$ regime of this equation is difficult to solve analytically, since $ϕ (t)$ depends on the entire history of growth cone movements. Simulations using different combinations of $a$ and $b$ are shown in Figure 1D. For the cases of $a \neq 0$ , after 150 time steps (12.5 hr of real time), the resultant turning angle was far from completely aligned with the gradient. Although the bias term bent the trajectory in the direction of the gradient, there was a straightening effect due to the persistence term, constantly pulling the growth cone toward the overall growth direction of the axon. As expected, the pull due to the gradient increased with larger b (Figure 1D). Thus, the persistence term prevented the axon from completely aligning with the gradient. Also apparent is that without noise, the trajectories were all very straight (with straightness index [see 'Materials and methods'] greater than 0.98). Thus, the microscopic constraint imposed by the persistence term leads to the macroscopic phenomenon of incomplete turning.

When we introduced Gaussian noise into the bearing changes (in radians) $(ξ ~ N (0, σ), σ = π / 4)$ with the same parameters and initial conditions as above for 1000 axons, the behavior was qualitatively similar: after an initial period of relatively rapid turning, turning angles tended to an almost steady state which was not aligned with the gradient even after a long time. However, the average final turning angle was even less than that of the noiseless case. This is because the noise created more random wandering of the growth cone, further reducing the directional effect of the gradient (Figure 2A–B). After 20–40 min, for $b$ = 0.1, the turning angle distribution of the population was 7 ± 25° (mean ± std). Assuming a normal distribution of turning angles, this means that many of the axons were no longer roughly perpendicular to the gradient, and thus only continued to turn extremely slowly. Therefore, over time the influence of the gradient on the whole population of axons weakened. The persistence term also created a resistance against large turns due to the gradient. Increasing $b / a$ increased the turning angle, but did not alter its rapid saturation with time (Figure 2C). Lastly, we examined the effect on the straightness by varying the standand deviation of the noise σ from 0 to π radians. As the steps became more noisy, the paths became less straight (Figure 2D).

Figure 2

Download asset Open asset

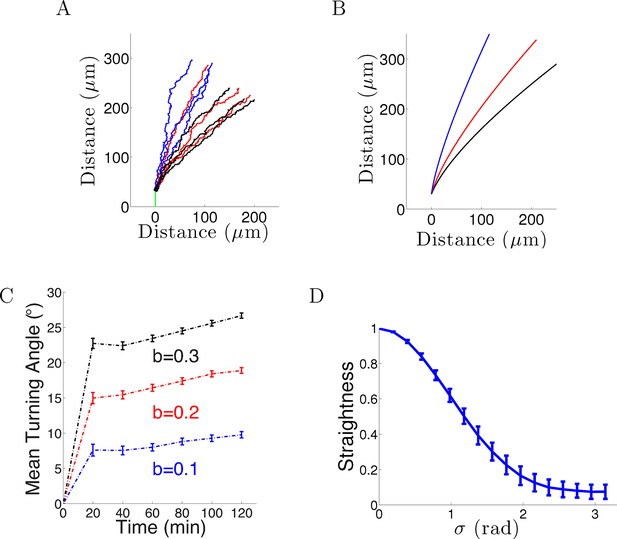
Model results with noise.

(A) Long-term behavior of growth cones: Simulation of 9 axons with fixed growth rate and noise in bearing changes (ξ ∼ N(0, *π/4*) radians) starting at ϕ(0) = 90° subject to the gradient direction Ψ = 0 with persistence $a$ = 1 and bias $b$ = 0.1 (blue), $b$ = 0.2 (red) and $b$ = 0.3 (black) after 150 steps (12.5 hr of real time). (B) The trajectories with the same parameters without noise. (C) The turning angles over time (mean ± SEM) of 1000 axons for different values of $b$ (0.1,0.2, 0.3) and $a$ = 1. (D) Straightness (mean ± std) decreases as the noise variance increases.

https://doi.org/10.7554/eLife.12248.006

Figure 2—source code 1 The code to simulate the trajectories based on Equation 1 in the noisy case.: https://doi.org/10.7554/eLife.12248.007
Download elife-12248-fig2-code1-v2.zip

In summary, the noiseless case generated very straight axons and growth cone angles that followed power laws with respect to time in the long time limit. Similarly, in the noisy case, the rate of change of the average turning angle was initially rapid and then slowed down even more rapidly with time. In both cases, the persistence term was a limiting factor on how much and how fast the axons could turn. Thus, this model captures, at least qualitatively, the behavior that axons turn only slightly in gradients, and even for long times do not generally become completely aligned with the gradient.

Stable gradient generation for guidance assays

Having established the basic behaviour of the model, we then asked whether it could reproduce in detail real axon trajectory statistics. We therefore analyzed the trajectories of superior cervical ganglion neurons in a new microfluidics device (Figure 3A–C). This device generated linear gradients, by the mixing of high and low solutions of a chemotropic factor. The gradient was visualized using 40 kDa dextran-tetramethylrhodamine (Figure 3D), and gradients were stable for at least 20 hr (Figure 3E,F).

Figure 3

Download asset Open asset

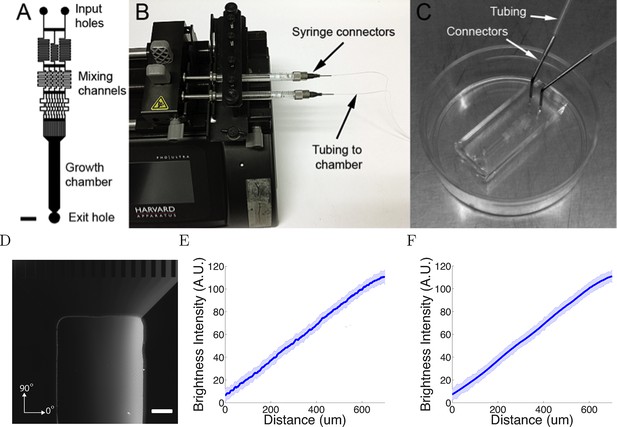
The microfluidic assay.

(A) The design of the chamber: the two solutions were pumped into the inlets and mix in the mixing channels before flowing into the growth chamber where the cells are plated. The mixing channels were of height 50 μm and width 50 μm. Scale bar 1 mm. (**B, C**) Photo of the experimental setup: two glass syringes attached to a Harvard pump injected the solutions into the chamber bonded on a 35 mm plastic plate. (D) Two solutions, one of which contained 0.1% (v/v) dextran fluorescently labelled with tetramethylrhodamine, were used to visualize the gradient. Brighter regions indicate higher concentrations. Scale bar 200 μm. (**E, F**) Line-scan measurements of fluorescence intensity across the device show a linear gradient which persists for at least 20 hr ( $t$ = 0h (E) and $t$ = 20h (F) ). The shaded errorbars show standard deviations across 10 chambers.

https://doi.org/10.7554/eLife.12248.008

Figure 3—source data 1 The average brightness intensity and noise in the microfluidic chamber at 0 and 20 hr. The average and noise were estimated from 5 min interval timelapse imaging over an 1-hr period.: https://doi.org/10.7554/eLife.12248.009
Download elife-12248-fig3-data1-v2.xlsx

SCG neurons were guided in the microfluidic assay

We measured the response to nerve growth factor (NGF) gradients of axons from dissociated P1-P3 SCG neurons. We chose this model system because almost 100% of these neurons express the NGF receptor TrkA (Wetmore and Olson, 1995; Verge et al., 1992).

Three conditions were investigated: a control without flow or gradient, an attractive gradient of nerve growth factor (NGF), and a gradient of NGF with added KT5720, which converts attraction to repulsion by lowering levels of cAMP in the growth cone (Song et al., 1997). Cells were injected into the growing chambers and grown for 2 hr before gradient onset. In the control condition, cells were grown over several hours with 0.3 nM NGF. In the NGF gradient condition, two solutions of concentrations 0 nM and 10 nM NGF were pumped into the growing chamber through the two inlets. Previous work using Scatchard analysis estimated that K_d = 0.9 ± 0.3 nM (Wehrman et al., 2007) and showed that SCG neuronal outgrowth is severely inhibited at the saturating NGF concentration of 40 nM (Ohta et al., 1990). Given the healthy growth in our assay, it is clear that the concentration in the gradient condition was below saturation point. We analyzed trajectories for 300 axons per condition. These were obtained from 23 individual chambers in the control case, 27 chambers in the NGF gradient case, and 24 chambers in the NGF gradient plus KT5720 case. In most experiments, 2 chambers were run in parallel, so the total numbers of experiments in each case were 12, 15, and 13, respectively. For the measurement of turning angles, we selected only axons that started growing between 70° and 110° relative to the gradient (when present). An asymmetric concentration field of guidance cue across the growth cone leads to turning (Song et al., 1997; Hentschel and Ooyen, 1999; Xiang et al., 2002; Ming et al., 2002) and axons growing in this range experienced between 94% (i.e. sin 70°) to 100% (i.e. sin 90°) of the maximum possible concentration difference across the growth cone. Thus, we expected the impact of the gradient would be strongest on these axons (Figure 4A). We tracked the growth cones every 5 min for as long as possible until they collapsed or branched or collided with other cells, axons or the edges of the chamber. The SCG axons were clearly attracted in the NGF gradient (Figure 4B). When the protein kinase A inhibitor KT5720 was added to the high and low solutions at concentration 70 nM, attraction was converted into repulsion as previously described (Song et al., 1997; Forbes et al., 2012) (Figure 4B). These results confirm that the gradient in the microfluidic assay elicited a guidance response in SCG axons. From the timelapse imaging data, we then selected the subset of axons that did not branch or retract following growth for several hours in the attractive NGF gradient, and measured the turning angles of the population over time. The average turning angle reached the steady state quickly and did not increase significantly with time, matching the prediction of the model (Figure 4C).

Figure 4

Download asset Open asset

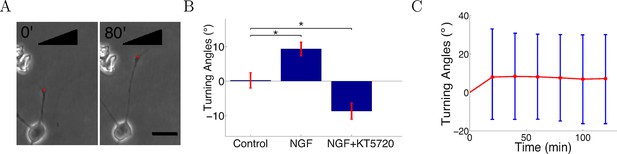
Turning in microfluidic gradients.

(A) Images of a representative axon initially almost perpendicular to the gradient at the beginning and end of the measurement after 80 min. Scale bar 20 μm. The red dots are the positions of the growth cone. (B) Summary of turning angles in the three conditions (mean ± SEM): control 0.2 ± 2.1° (n=120), NGF gradient (0–10 nM) 9.3 ± 1.9° (n=143), NGF gradient (0–10 nM) + KT5720−8.8 ± 2.2° (n=112). *: p < 0.01 t-test in both cases. (C) The means (red) and standard deviations (blue) of turning angles of 143 axons over time for the attractive case.

https://doi.org/10.7554/eLife.12248.010

Figure 4—source data 1 The turning angles at different time points from the start of the experiment.: https://doi.org/10.7554/eLife.12248.011
Download elife-12248-fig4-data1-v2.xlsx

The gradient did not affect axon branching

One possible way that the gradient could affect the axons is by causing biased branching [c.f. (Simpson et al., 2013)], or changes in branching rates. To test whether the NGF gradient changed the branch extension and retraction rates, we compared the number of branches per cell after 5 hr of growth and did not detect any difference (p = 0.9 Kolmogorov–Smirnov test, Figure 5A). We measured the intervals between successive branching events in the same cell in each condition and did not find any difference in the branching rate (p = 0.7 Kolmogorov–Smirnov test, Figure 5B). Similarly, the lifetimes of the branches were unaffected by the gradient (p = 0.2 Kolmogorov–Smirnov test, Figure 5C). We counted the number of branches pointing up and down the gradient per cell and did not find any difference (p = 0.8 Kolmogorov–Smirnov test, Figure 5D). Thus, the gradient had no effect on axon branching and retraction.

Figure 5

Download asset Open asset

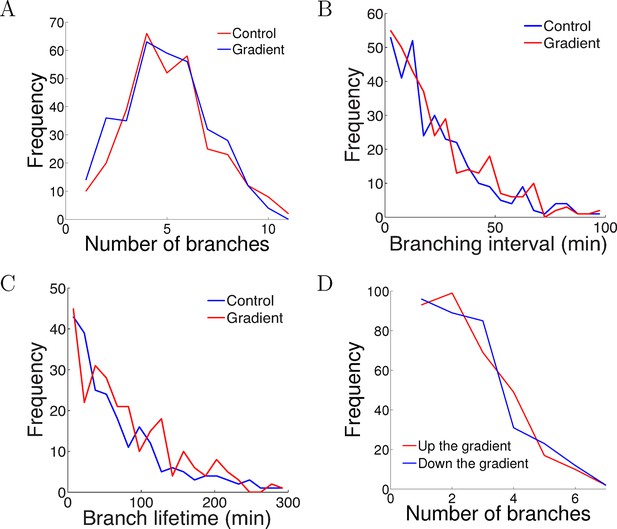
The gradient did not affect branch extension and retraction rates.

(A) Histogram of the number of cells with different numbers of branches after 5 hr of growth. The number (mean ± std) of branches per neuron in the control condition was 4.2 ± 1.8 (n=324 cells) and in the gradient condition was 4.4 ± 1.9 (n=297 cells), p = 0.9 Kolmogorov–Smirnov test. (B) The distribution of interval times between two successive branching events of the same cell. The interval (mean ± std) in the control condition was 23.1 ± 22.8 min (n=315 intervals) and in the gradient condition was 24.1 ± 23.5 min (n=287 intervals), p = 0.7 KS test. (C) Branch lifetime (mean ± std) in the control condition was 87 ± 79 min (n=245 branches) and in the gradient condition was 92 ± 81 min (n=213 branches), p = 0.2 KS test. (D) Histogram of the number of branches pointing up the gradient vs down the gradient (p = 0.8, KS test).

https://doi.org/10.7554/eLife.12248.012

Figure 5—source data 1 The number of branches per cell after 5 hr of growth in the control and NGF gradient (Columns A,B). In the gradient, we counted the number of branches pointing up and down the gradient (Columns C,D). We measured the time intervals between successive branching events in the same cell in the control and NGF gradient over 5 hr (Columns E-F). For branches that retracted in the 5 hr imaging time, we measured their lifetimes in the control and NGF gradient (Columns G,H).: https://doi.org/10.7554/eLife.12248.013
Download elife-12248-fig5-data1-v2.xlsx

Flow did not affect the statistics of steps

To test whether fluid flow in the chamber biased the statistics of the steps, axons growing in the gradient condition with fluid flow were divided into four quadrants with different relative angles to the fluid flow: two quadrants growing perpendicular to the flow, one quadrant growing with the flow, and the other growing against the flow (Figure 6A). Comparing the distribution of bearing changes between the four quandrants, and with axons from the control condition without any flow, showed no influence of the flow (p = 0.7 in Figure 6B and p = 0.4 in Figure 6C, Kruskal-Wallis test). The means of the bearing changes in quadrants 2 and 4 were non-zero, and the bearing changes accumulated over time to result in a non-zero average turning angle of the population. However, these differences in means were very small (approximately 1°), and there were no significant statistical difference among the distributions. Therefore, the positive turning angles in the NGF gradient (and negative turning angles in the NGF gradient + KT5720) were due to the effect of the gradient, not bias from the flow.

Figure 6

Download asset Open asset

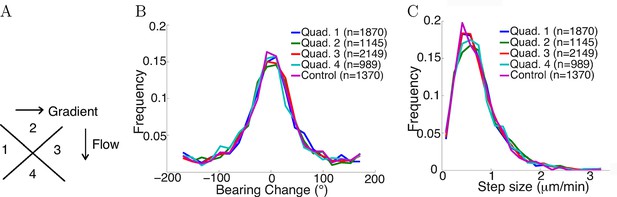
Flow did not affect step statistics.

(A) Axons growing in different directions were grouped into four quadrants. (B) Growth cones’ step sizes in different quadrants. n values refer to the number of steps in each quadrant. There was no significant difference between the quadrants (p = 0.7 Kruskal-Wallis test). (C) Grow cones’ bearing changes in different quadrants (p = 0.4 Kruskal-Wallis test).

https://doi.org/10.7554/eLife.12248.014

Figure 6—source data 1 We divided the axons into four quadrants as explained in Figure 6 and measured the bearing changes and stepsizes in each quadrant. This file contains the step sizes (Sheet 1) and and bearing changes (Sheet 2) in the control condition (Column A) and in each quadrant of the NGF gradient condition (Columns B-E).: https://doi.org/10.7554/eLife.12248.015
Download elife-12248-fig6-data1-v2.xlsx

Growth cone trajectories were generally straight

Axon growth is shown in Videos 1–3 and Figure 7A–C. The growth cone often wandered quite randomly, but nevertheless usually the axon segment remained very straight from the growth cone to the cell body or last axon branch point (Figure 7A–C). This implies that often the entire axon segment was pulled sideways across the substrate (as can be seen directly in the movies). Thus, despite the irregular trajectory of the centre of the growth cone, the tension force on the growth cone from the axon was usually pointing directly back to the last anchor point, consistent with the assumptions of the model. To quantify this further, we measured the angle of this 20 μm segment and the angle to the anchor point ϕ and found them to be almost the same (Figure 7D,E). Thus, we can understand the term ϕ as the tension due to the most distal segment.

Figure 7

Download asset Open asset

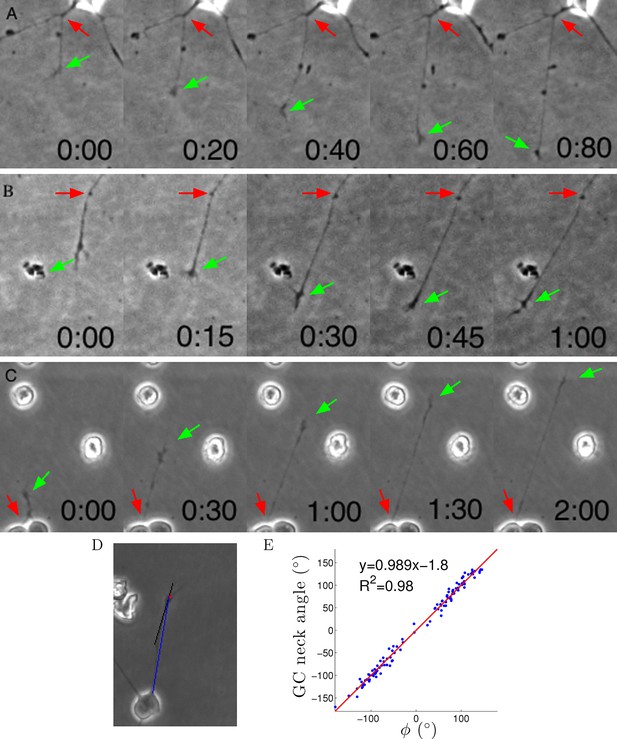
Axons were dragged by growth cones.

(**A–C**) Timelapse images of three example growth cones. Red arrows point to the putative anchor points and green arrows point to the growth cones. Time is shown in hours and minutes. (D) We measured the angle of the neck of the growth cone (the last 20 μm, black line) and the overall growth cone angle (blue line) after 1 hr from the start of the experiment. (E) The two angles were highly correlated, due to the straightness of the axon.

https://doi.org/10.7554/eLife.12248.016

Figure 7—source data 1 We measured the angle of the growth cone from its putative anchor point (Column A) and compared with the angle of the most distal 20 μm segment of the axon (Column B) 1 hr after the start of the experiment.: https://doi.org/10.7554/eLife.12248.017
Download elife-12248-fig7-data1-v2.xlsx

Video 1

Download asset

posterframe for video — Timelapse images of an example growth cone.

One-minute interval phase contrast timelapse imaging of a growth cone in a microfluidic chamber.

https://doi.org/10.7554/eLife.12248.018

Video 2

Download asset

Video 3

Download asset

The trajectories (i.e. the locus of the centre of the growth cone) in three conditions are plotted in Figures 8–10. Note that these paths are not the same as the final image of the axon, which generally pointed straight back from the final position of the growth cone to the anchor point. Visually, the paths appear mostly straight with occasional large turns, consistent with a long tail for the bearing change distribution. The mean straightness index for the trajectories was S = 0.72 (Figure 11A).

Figure 8

Download asset Open asset

Trajectories of 300 axons growing over 80 min in the control condition, ordered by the initial angle.

The red segments indicate the initial direction of the axon and the blue segments show the traces of the growth cones’ trajectories. Scale bar = 100 μm.

https://doi.org/10.7554/eLife.12248.021

Figure 9

Download asset Open asset

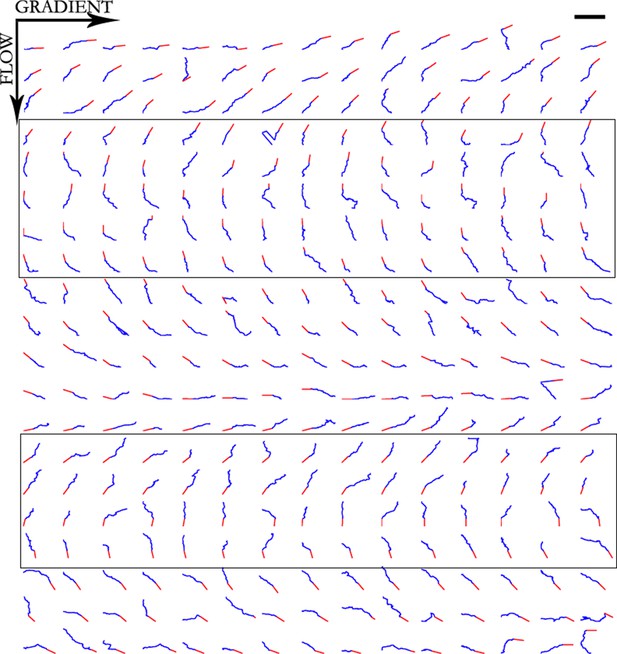
Trajectories of 300 axons growing over 80 min in the NGF gradient, ordered by the initial angle.

Only axons in the box were selected for turning angle measurements as they were almost perpendicular to the gradient, hence most affected by it. Scale bar = 100 μm.

https://doi.org/10.7554/eLife.12248.022

Figure 10

Download asset Open asset

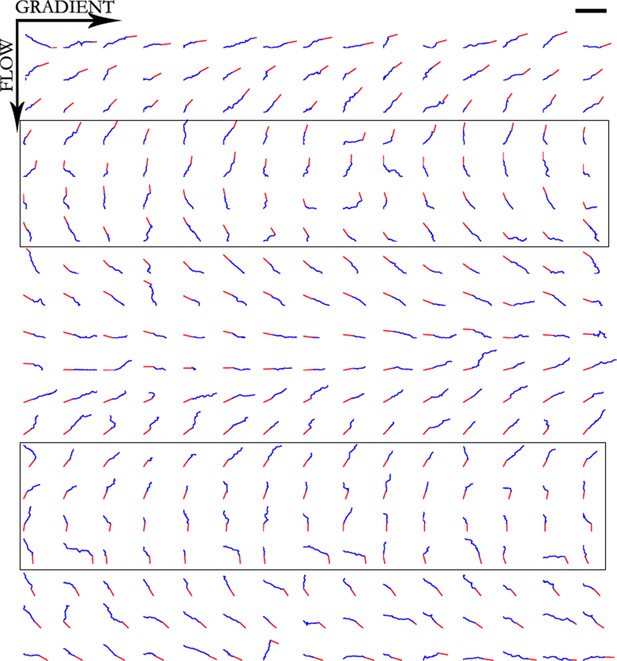
Trajectories of 300 axons growing over 80 min in the NGF gradient with 70 nM KT5720 added, ordered by the initial angle.

Only axons in the box were selected for turning angle measurements. Scale bar = 100 μm.

https://doi.org/10.7554/eLife.12248.023

Figure 11

Download asset Open asset

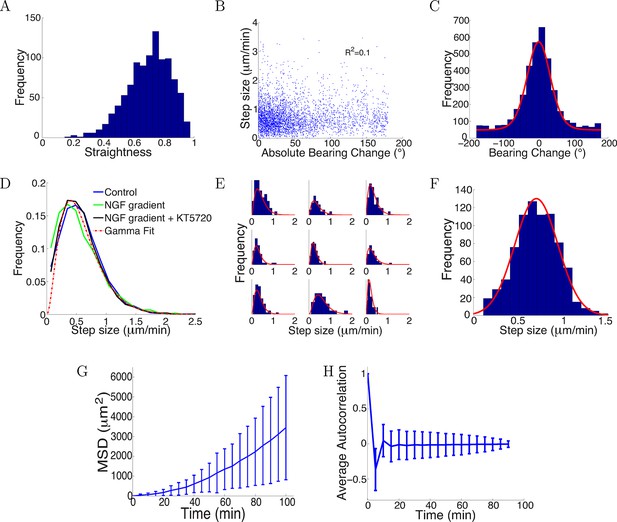
Trajectories were straight with step sizes and bearing changes independent of each other.

(A) Distribution of straightness indices of all paths with mean straightness of 0.72. (B) There was no correlation between bearing change and step size (R² = 0.1, p = 0.7). (C) The distribution of bearing changes (blue) in radians in the control condition can be fitted to a mixture of two von Mises distributions (red) $P (x) = 0.5 \frac{\exp (3 \cos (x))}{2 π I_{0} (3)} + 0.03$ . (D) Step sizes in the control, attractive and repulsive gradients conditions were similar and well-fitted by the gamma distribution P(x) ∝ x² exp(−x/24) (red). (E) Step sizes of individual growth cones (blue) can be described by gamma distributions (red) (9 examples shown). (F) This distribution of the average step sizes (blue) of individual growth cones was well-fitted by a Gaussian distribution N(0.7, 0.24) (red). (G) Mean square displacement and standard deviation of 300 growth cones growing over 100 mins in the control condition was super-linear, indicating that growth cone trajectories were straighter than predicted by a simple random walk. (H) Autocorrelation of bearing changes (mean ± std) showed that successive bearing changes were anti-correlated.

https://doi.org/10.7554/eLife.12248.024

Figure 11—source data 1 From our 5-min interval tracings, we measured the bearing changes and step sizes in the control condition (Columns A, B), the mean step sizes of all the growth cones (Column C) and the step sizes in the NGF gradient and NGF gradient + KT5720 conditions (Columns D,E).: https://doi.org/10.7554/eLife.12248.025
Download elife-12248-fig11-data1-v2.xlsx

Step size and bearing change distributions were similar across conditions

There was little correlation between the bearing change magnitude and step size (Figure 11B). The distribution of bearing changes in radians was well fitted by a mixture of a von Mises and a uniform distribution (−π < x < π) (Figure 11C). That is there was a great deal of randomness in bearing changes, but with a peak in probability near the forward direction. Thus, growth cones tended to move in a straight line instead of turning uniformly randomly. This is inconsistent with the assumptions of several previous models (Buettner et al., 1994; Odde and Buettner, 1995; Maskery et al., 2004).

Accumulating across all the growth cones, the distributions of step sizes over 5 min were statistically indistinguishable across the three conditions (Kruskal-Wallis test p = 0.35), and were well fitted by a gamma distribution (Figure 11D). That is, the most likely step size was around 0.5 μm/min, but the distribution had a long tail, so that longer step sizes were also seen. The distribution of step sizes for each individual growth cone were also well fit by gamma distributions (Figure 11E). However, individual growth cones had idiosyncratic mean values. The distribution of these mean values could be well fitted by a Gaussian distribution (Figure 11F).

Nevertheless, the mean square displacement was clearly not linear, implying that a simple random walk is not suitable to describe the movement (Figure 11G). Successive steps were anti-correlated (Figure 11H), which was not accounted for in a previous model (Pearson et al., 2011). This helps the paths remain relatively straight: if successive steps were positively correlated, the paths would become more bent over time. Due to large noise in the bearing changes, bearing changes more than one step apart were uncorrelated.

Turning angles over time were well predicted by the model

Having established the key statistics of steps from the data, we now asked if the simple model in Equation (1) could replicate the observed trajectories and explain the phenomenon of saturated turning. We sampled the mean speed $v_{m e a n}$ of each growth cone from a truncated Gaussian distribution of mean 0.7 μm/min and standard deviation 0.24 μm/min. At each time point (5-min interval), the growth cone sampled a step size from the gamma distribution $Γ (4 ∕ u, v_{m e a n} * u ∕ 4)$ where u was a uniform random number. The bearing changes evolved according to Equation (1). We found that the random noise ξ in bearing changes (in radians) could be well fit by the mixture von Mises distribution

P (ξ) = c \frac{\exp (d \cos (ξ))}{2 π I_{0} (d)} + (1 - c)

where $c$ and $d$ are parameters to be fit. This distribution is not necessarily the same as that of the bearing changes in Figure 11F. As the bearing change is the sum of three random terms, its distribution is broader than the distribution of the noise term. To estimate the four free parameters $a, b, c, d$ , we input the initiation angles $ϕ (0)$ and used the model to generate the distribution of turning angles $ψ_{t u r n}$ . We then estimated the likelihood function that the turning angle data was generated from the model with the given parameters $L (ψ_{t u r n} | a, b, c, d, ϕ (0))$ .

We found the values of $a, b, c, d$ that maximized the likelihood (the parameters mostly likely to have generated our empirical turning angle data) were $a$ = 0.7, $b$ = 0.09, $c$ = 0.75, $d$ = 6. The statistics over 5000 simulated trajectories using these parameters are shown in Figure 12, and some example trajectories are shown in Figure 13. Similarly, we fitted the model to the control data and repulsive gradient and found $b$ = 0.002 and $b$ =−0.08, respectively, with other parameters remaining at very similar values as before. Notably, the simulated turning angles changed little over time (Figure 12A), consistent with our preliminary prediction and the data (Figures 1E, 4C). Thus, with realistic step sizes and bearing change noise distributions, the model was able to capture the phenomenon of saturated turning with quantitatively accurate means and variances over time. The distribution of turning angles and step sizes also closely matched the real data (Figure 12B,C). The simulated straightness distribution was also very smilar to the real distribution (p = 0.2, t-test) (Figure 12D). The model also captured the distribution of bearing changes, the mean square displacement and the anticorrelation between successive bearing change, which was a consequence of the persistence term straightening the paths (Figure 12D–F). If successive steps were positively correlated, the paths would become more bent over time. This correlation was rapidly lost beyond one time lag because of the large noise.

Figure 12

Download asset Open asset

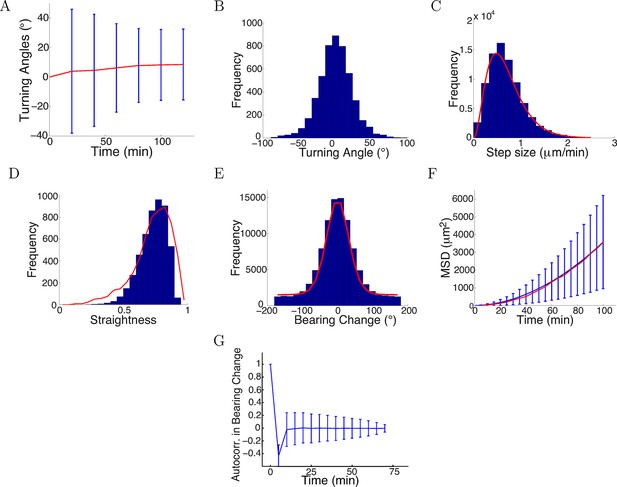
Model captured key statistics of trajectories.

(A) The evolution of simulated turning angles (mean ± std) of n=5000 growth cones over time in the attractive gradient condition. (B) Simulated turning angles after 16 steps (80 min) had mean 9.8° and standard deviation of 24.2°, similar to the empirical data in red in Figure 4B. (C) Distribution of simulated step lengths (blue), fitted with the empirical distribution (red). (D) Straightness of simulated trajectories (mean 0.75, blue), compared with empirical distribution (red) (p = 0.2, t-test). (E) Simulated bearing changes (blue) fitted with the mixture of von Mises distributions given in Figure 11D (red). (F) Mean square displacement of simulations (blue) and data (red). (G) Autocorrelation of simulated bearing changes.

https://doi.org/10.7554/eLife.12248.026

Figure 12—source code 1 The code to simulate the trajectories based on Equation 1 with the step sizes and bearing changes described in Section Turning angles over time were well predicted by the model.: https://doi.org/10.7554/eLife.12248.027
Download elife-12248-fig12-code1-v2.zip

Figure 13

Download asset Open asset

Simulated trajectories from three conditions.

(A) control, (B) NGF gradient, (C) NGF gradient + KT5720.

https://doi.org/10.7554/eLife.12248.028

Unlike previous models, we did not assume constant steps or a uniform distribution of bearing changes but rather derived these from empirical data. The model was then able to predict the evolution of the average turning angle over time, the straightness profile and the anticorrelation in bearing changes. Most importantly, it could explain the phenomenon of slow and saturated turning, due to a weak bias term relative to the persistence term. A microscopic factor in each step led to a macroscopic phenomenon of limited, variable turning and straight paths. This often overlooked feature of axon growth turned out to be critical in our model in limiting the overall turning. We also found little difference between the attractive and repulsive case, indicating that attractive and repulsive gradients employed similar mechanisms and could not reduce the variability of axon trajectories.

Multiple anchor points achieved sharp turns but also increased variability

The in vitro data we have presented here was well-fitted by assuming the only anchor point is where the axon emerges from the soma or the branch point. However, the in vivo environment is much more complex, and axons may establish anchor points with the substrate at multiple positions as they extend. We therefore investigated in the model what effect this would have on turning angles. We assumed that at each timestep, the probability of that point becoming a new anchor point was fixed, while leaving the evolution at each step as before. The average number of anchor points per timestep (i.e. 5 min) is denoted by r. We analyzed two cases: anchoring probabilistically at each time step (Figure 14A–C), and anchoring at regular intervals (Figure 14D–F). We simulated the trajectories for T = 150 timesteps with the same parameters as Figure 2A ( $a$ = 1, $b$ = 0.1, ξ = 0 or ξ ∼ N (0, π/4) radians). In both cases, more anchor points led to sharp turns in the trajectories and larger mean turning angle (Figure 14G), since the growth cone now was more free from its initial position. However, it increased the variability in the turning (Figure 14G). Given the same rate of anchoring, whether the growth cone put down new anchor points probabilistically or regularly made little difference to the mean turning. We compared the mean square final angle $⟨ ϕ {(T)}^{2} ⟩$ which is the sum of the bias ${⟨ ϕ (T) ⟩}^{2}$ and the variance $(ϕ (T))$ . Ideally, the growth cone should completely align with the gradient, that is $ϕ (T) = 0$ . Figure 14H shows the bias/variance trade off. Although more anchor points introduced larger variance in the final angle, they achieved greater turning, that is smaller $ϕ (T)$ . Figure 14I shows that in the case without movement noise (ξ = 0) and regular anchoring, the growth cone angle $ϕ (t)$ also followed a power law in the large t limit, similarly to the case without anchoring (Figure 1C). However, the exponent of this power law was larger, demonstrated by a steeper slope between log( $t$ ) and log(ϕ( $t$ )), meaning that the growth cone aligned with the gradient faster with more anchor points. Thus, increasing the rate of anchoring leads to stronger turning, but increases the variance of the responses.

Figure 14

Download asset Open asset

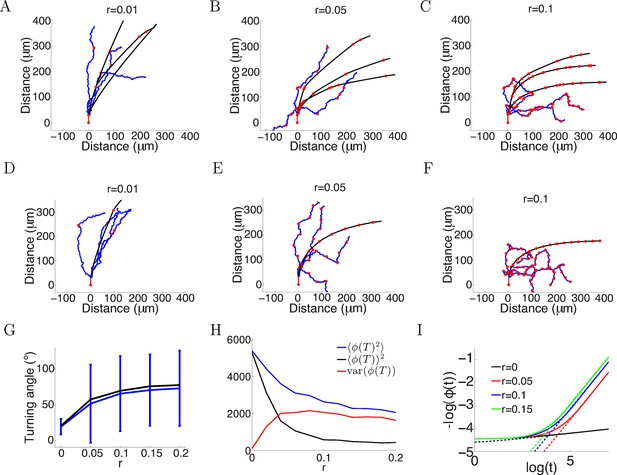
More variability with more anchor points.

(**A–C**) Trajectories of growth cones with probability of putting down a new anchor r= 0.01, 0.05, 0.1 at each timestep and the same parameters as Figure 2A (a = 1, b = 0.1, T = 150 timesteps). The black plots are without noise in the bearing changes, the blue plots are with noise $ξ ~ N (0, π / 4)$ radians in the bearing changes and the red dots are the anchor points. More anchor points lead to higher variability but also stronger turning. The means and standard deviations of turning angles and the values for the noiseless versus the noisy case in brackets for r = 0.01, 0.05, 0.1 are 32 ± 9° (30 ± 36°), 55 ± 8° (49 ± 57°) and 67 ± 5° (60 ± 56°), respectively. (**D–F**) Trajectories of growth cones with the same rate of putting down new anchor points as A-C but at regular intervals. The means and standard deviations of turning angles and the values for the noiseless versus the noisy case in brackets are 27° (24 ± 17°), 57° (54 ± 51°), 69° (66 ± 51°). (G) The means and standard deviations of turning angles after 150 timesteps as a function of the anchoring rate at regular intervals in the noiseless and the noisy case. (H) The mean square of the final growth cone angle (in degrees) $⟨ ϕ {(T)}^{2} ⟩$ for different anchoring rates r after 150 steps. $⟨ ϕ {(T)}^{2} ⟩$ is the sum of the bias term ${⟨ ϕ (T) ⟩}^{2}$ and the variance term var( $ϕ (T)$ ). Although more anchor points add more variance to the final angle (red curve), they achieve stronger turning $ϕ (T) \approx 0$ (black curve). (I) The evolution of $ϕ (t)$ over time, for the case of anchoring at regular intervals and no noise in the movement (ξ = 0). With more anchor points, $ϕ (t)$ also follows the power law but with steeper slope, meaning that $ϕ (t) \to 0$ at a faster rate than the case without anchor points.

https://doi.org/10.7554/eLife.12248.029

Figure 14—source code 1 The code to simulate the trajectories based on Equation 1 with normally distributed noise in bearing changes described in Section Multiple anchor points achieved sharp turns but also increased variability. In the regular anchoring case, the growth cone position after every 1/r steps becomes a new anchor point. In the probabilistic anchoring case, each growth cone position has a probability of r to become a new anchor point. growth-cone-tracker-5min. Growth cone tracking code. The code tracks the position of the growth cone centre every 5 mins from timelapse AVI files. extract-GC-positions. Growth cone position extraction code. The code to extract the position of the growth cone from the tracings.: https://doi.org/10.7554/eLife.12248.030
Download elife-12248-fig14-code1-v2.zip

Discussion

Here, we presented a model of axon trajectories in gradients and helped resolve the mystery of why axon turning angles in gradients saturate over time in vitro, revealing an important factor limiting axon turning. We found that the movement of the growth cone was strongly influenced by the axon’s tendency to maintain a straight trajectory forward, limiting the directional effect of the gradient and preventing the axon from aligning with the gradient even after a long time. Our model predicted that, averaged over a large population of axons, the initial rate of turning drops rapidly over a short period of time (20–40 min). The model shows that adding more anchor points can give the growth cone more flexibility and produce larger average turning, but also increases the variability. Thus, we predict that different substrates, producing different densities of anchor points, could result in different trajectories for the same the gradient conditions.

The application of forces to axons can induce rapid elongation without axonal thinning, and thus stretch can stimulate growth (Suter and Miller, 2011). Furthermore, stretch can also regulate the mode of growth. When axons are tightly bound to a sticky substrate, stretching only happens at the tip and axons elongate by tip growth. In contrast, if axons grow relatively unattached to the substrate, they will lengthen by stretching due to the pull of the growth cone (Chang et al., 1998; O'Toole et al., 2008), which appears to be the case in our experimental condition. The tension along the axon will cause stimulation of growth in the existing direction producing straighter trajectories. The stiffness of axons is also important (Rajagopalan et al., 2010), and stiffer axons will likely have higher persistence due to their more limited ability to bend.

This tension results from cytoskeletal coupling with adhesive interactions to the substrate and is critical to growth cone migration (Heidemann et al., 1997; Spire, 2009). Although anchor points are an abstraction in our model, their biological implementation may be focal adhesions. Only at these points is the axon firmly attached to the substrate. There is a number of ways in which anchor points could be investigated experimentally in future work. Axons could be stained for proteins such as integrins (Kaverina et al., 2002) to test whether their distribution is strongly localized to particular points along the axon. We also predict that applying force orthogonal to the direction of axon growth, for instance by using a pipette to puff liquid at different locations along the axon, would cause a deflection of the axon of a size related to the distance from the nearest anchor point. A similar experiment was performed using a glass needle to tow axons (O'Toole et al., 2008). It was observed that the distal region of the axon was free of the substrate, while the proximal region was firmly attached. In addition, it could be possible to determine the internal stress field of an axon, as has been done for growth cones (Betz et al., 2011): we would expect the stress to in general be different on the two sides of an anchor point. The density of anchor points will depend on the components of the extracellular matrix (ECM). In our experiments, on laminin, they appeared to be rare. This might be because adhesion points are expensive to produce and the axon can grow faster when it is not attached to the substrate (Chang et al., 1998). However, the biological factors governing when new anchor points are generated are unknown.

Tension is also dependent on cell type and two main properties of the substrate: stiffness and ECM components. Our data comes from peripheral nervous system (PNS) neurons growing on a laminin substrate that is hard rather than gel-like, and other cell types of different substrates might have different behaviours. Central nervous system (CNS) and PNS neurons have different sensitivities to substrate stiffness due to adaptation to their natural environments (Koch et al., 2012), and traction force in vitro increased on stiffer substrates (Koch et al., 2012). Substrates with different ECM components differentially promote growth cone motility and point contact formation. For example, growth cones are more highly motile and neurites extend more rapidly on laminin than fibronectin because point contacts have higher turnover rate (Robles and Gomez, 2006).

Overall, our work suggests that without many anchor points, cues additional to gradients may be necessary for axons to reliably find their targets in vivo (unless the motility noise is for some reason much lower in vivo than in vitro). These could include mechanical cues and axon-axon interactions. To understand such interactions, it is important to generate assays with realistic substrates suitable for different cell types. Recent 3D culture models, in which cells are grown with a protein scaffold, can capture some aspects of the tissue environments instead of hard surfaces (Cullen et al., 2007). It will be interesting to see how different ECM properties lead to changes in trajectories and whether they can facilitate more reliable turning.

In conclusion, we have presented a simple mathematical model which gives accurate quantitative predictions of the properties of axonal trajectories in a microfluidics-based in vitro gradient assay. The model identifies the key importance of anchor points in controlling turning and provides an explanation for why axonal turning in gradients in vitro tend to saturate rapidly at small turning angles. This model provides a predictive framework which can be used to test whether axonal trajectories observed in vivo can be explained purely in terms of gradient guidance, or whether additional guidance mechanisms are also required.

Materials and methods

Microfluidics chamber fabrication

Request a detailed protocol

The device was designed in AutoCAD 2013 based on the pattern in (Dertinger et al., 2001). The microfluidic master molds were prepared by standard soft photolithography techniques. The silicon wafer (M.M.R.C. Pty Ltd) was coated with a 50 μm thick layer of SU-8 2100 relief (MicroChem, Westborough, MA) with a spincoater (EVG). The master was printed onto high-precision photoplates (Konica-Minolta) with a photoplotter (EVG). Before replica moulding, the silicon master was silanized with vapour phase silane, under vacuum for 1 hr at room temperature to prevent polydimethylsiloxane (PDMS) adhering to the master.

PDMS base elastomer (Sylgard 184, Dow Corning, Midland, MI) and silicon elastomer curing agent in a 10:1 (m/m) ratio were thoroughly mixed and poured on the master to a depth of about 4 mm. The mold with PDMS was degassed in a vacuum chamber for 2 hr and baked at 80°C for 2 hr. The PDMS replica was then peeled from the silicon wafer and cut into individual chambers. Holes were cored in the PDMS chambers using a 0.75 mm corer (Harris Uni-Core). To bond the PDMS chamber to a plastic tissue-culture petri dish, the dish and the chamber were plasma treated at 100W at a pressure of 380 mTorr for 40 s. The plate was then covered with (3-Aminopropyl)triethoxysilane (APTES, Sigma-Aldrich) solution (5% APTES in 70% ethanol). The plastic dish was washed thoroughly with water, air dried, and the chamber was pressed onto the dish. To avoid air bubbles forming, the dish was filled with distilled water and degassed in the vacuum chamber for 10 min before use.

Primary superior cervical ganglion (SCG) cell culture

Request a detailed protocol

SCG neurons were harvested from postnatal day 1–3 Wistar rat pups. The SCGs were then cut into thirds, incubated in 0.25% trypsin (GIBCO) at 37°C for 30 min and then triturated through a flamed-polished Pasteur pipette for 5 min to dissociate individual cells. The growth solution was Opti-MEM solution (GIBCO) containing 1X penicillin/streptomycin, 10 μg/mL mouse laminin, 4% (v/v) fetal calf serum, 2% B-27 supplement (Life Technologies), and 0.3 nM NGF. The cells were suspended in the growth solution and injected in the microfluidic chamber using a 100-μL glass syringe (SGE Analytical Science).

Gradient generation and measurement

Request a detailed protocol

Two syringes were filled with either the high (10 nM) or low (0 nM) NGF solution. The high solution contained 0.1% (v/v) 40 kDa-dextran fluorescently labelled with tetramethylrhodamine to visualize the gradient. After the cells were seeded, the syringes containing the high and low solutions were connected to the chamber using polyethylene tubings. The chamber was moved to an incubated inverted microscope (Zeiss AxioObserver). The syringes were attached to a Harvard PHD pump and the flow rate was set at 10 μL/hr. After the flow had been started, fluorescent images of the chamber were taken in Zen software. Background intensity outside the chamber was subtracted from the images. The average brightness intensity and variations over time were then calculated across the chamber. A gradient of fluorescence confirmed that the NGF gradient had formed in the growth chamber. To generate a repulsive gradient, KT5720 (Alexis Biochemicals), a specific inhibitor of protein kinase A (PKA), was added into both the high and low solutions at a concentration of 70 nM.

Tracking growth cone trajectories

Request a detailed protocol

After the onset of the gradient, the axons were imaged every 5 min for 6 hr using Zeiss Zen software. After data acquisition, axons of 30 μm length, growing in all directions, that did not branch or retract in at least 80 min, were chosen for measurements. All axons were tracked manually using customized MATLAB software (The MathWorks) for as long as possible until they branched or retracted. A 5-min time interval was chosen because, for smaller intervals, variability in identifying the centre of the growth cone was larger than the net movement between frames. The point where the axon attaches to the cell body or the main branch was considered the anchor point.

The straightness index

Request a detailed protocol

The straightness index S is the inverse of tortuosity, and compares the overall net displacement G of a path with the total path length T (Codling et al., 2008). Consider a walk that starts at location $(x_{0}, y_{0})$ , and after n steps of lengths l_j (j = 1...n) finishes at $(x_{n}, y_{n})$ . The straightness index is given by:

S = \frac{G}{T} = \frac{\sqrt{(x_{n} - x_{0})^{2} + (y_{n} - y_{0})^{2}}}{\sum_{j = 1}^{n} l_{j}}

This index is between 0 and 1, where 1 corresponds to movement in a straight line and 0 corresponds to a walk that returns to the origin. The closer this index is to 1, the straighter the trajectory is. Obviously, $S$ depends on the time interval used for tracing but can be used to compare conditions, which all have the same time interval.

Modeling growth cone trajectories

Request a detailed protocol

All parameters of the model are summarized in Table 1. We consider a model which is a discretized random walk in which we separate the length and directions of the steps (Figure 1A). We discretized the axons at a timestep of 5 min, and, based on hypotheses we test later, only explicitly modelled the turning angles of the steps or ’bearing changes’. $Δ θ (t)$ , the ‘bearing change’ at time t depends on the current bearing of the growth cone $θ (t)$ , the angle $ϕ (t)$ of the vector connecting the growth cone to its anchor point, the gradient direction Ψ and the noise ξ according to Equation (1):

Δ θ (t) = a ∠ (ϕ (t), θ (t)) + b ∠ (Ψ, θ (t)) + ξ,

where two parameters $a$ and $b$ scale the contributions of the first term representing persistence and the second term representing the bias due to the gradient. The symbol $∠ (x, y)$ denotes the angle difference $x - y$ constrained to take values from −π to π. It is positive for an anticlockwise turn to get from $y$ to $x$ . As the bearing is biased by the gradient direction, the overall growth cone angle $ϕ (t)$ will also be biased by the gradient, coupled through the above equation.

We first assume there is only one fixed anchor point where the axon initially grew out of the cell body or the main branch. We will later relax this assumption and allow the growth cone to put down new anchor points along its path. We denote the rate of anchor point deposition as r, which is the inverse of the average number of steps per new anchor point.

We first assume an initial direction of $ϕ (0) = θ (0) = π ∕ 2$ , a gradient direction of Ψ = 0, and a fixed step size s every 5 min. In the idealized noiseless case (ξ = 0) as $t \to \infty$ , the equation reaches a steady state when $Δ θ = 0$ , that is:

∆ θ (t) = a (ϕ (t) - θ (t)) + b (0 - θ (t)) = 0 .

This gives:

θ (t) = \frac{a}{a + b} ϕ (t) = α ϕ (t)

with $α = \frac{a}{a + b}$ . Defining L to be the distance of the growth cone from its original position, and using the geometry in Figure 1A, we have:

\tan (ϕ (t + 1)) = \frac{L \sin ϕ (t) + s \sin (α ϕ (t))}{L \cos ϕ (t) + s \cos (α ϕ (t))} \approx \tan (ϕ (t)) + \frac{s \sin (α ϕ (t))}{L \cos ϕ (t)} - \frac{L \sin ϕ (t) s \cos (α ϕ (t))}{L^{2} \cos^{2} ϕ (t)}

The approximation above is due to $s$ ≪ $L$ and ϕ(t) → Ψ = 0 as t → ∞. Using the Taylor expansion f(x₀ + δx) ≈ f(x₀) + δxf’(x₀) and d tan⁻¹(x)/dx = 1/(x² + 1), we invert both sides of the above equation to obtain:

ϕ (t + 1) \approx \tan^{- 1} (\tan ϕ (t) + \frac{s \sin (α ϕ (t))}{L \cos ϕ (t)} - \frac{L \sin ϕ (t) s \cos (α ϕ (t))}{L^{2} \cos^{2} ϕ (t)}) \approx ϕ (t) + (\frac{s \sin (α ϕ (t))}{L \cos ϕ (t)} - \frac{L \sin ϕ (t) s \cos (α ϕ (t))}{L^{2} \cos^{2} ϕ (t)}) \cos^{2} ϕ (t) \approx ϕ (t) + s / L (\sin (α ϕ (t)) \cos ϕ (t) - \cos (α ϕ (t)) \sin ϕ (t)) \approx ϕ (t) + s \sin ((α - 1) ϕ (t)) / L

At $t \to \infty$ , $Δ θ (t) \to 0$ , meaning the growth direction aligns with the gradient, thus $ϕ (t) \to 0$ and $L \approx s t$ due to geometry (even for the $a$ = 0 case), so the above equation can be simplified as

\frac{d ϕ (t)}{d t} \approx \frac{(α - 1) ϕ (t)}{t}

\frac{d ϕ (t)}{ϕ (t)} \approx \frac{(α - 1) d t}{t}

\ln ϕ (t) = (α - 1) \ln t + const

Therefore, the long-term turning behaviour of axons in the model is given by the power law $ϕ (t) \propto t^{(α - 1)}$ .

References

1. Athamneh AI
2. Suter DM
(2015) Quantifying mechanical force in axonal growth and guidance
Frontiers in Cellular Neuroscience 9:359.

https://doi.org/10.3389/fncel.2015.00359
- Google Scholar
1. Betz T
2. Koch D
3. Lu Y-B
4. Franze K
5. Kas JA
(2011) Growth cones as soft and weak force generators
Proceedings of the National Academy of Sciences of the United States of America 108:13420–13425.

https://doi.org/10.1073/pnas.1106145108
- Google Scholar
(2008) Stochasticity and functionality of neural systems: mathematical modelling of axon growth in the spinal cord of tadpole
Bio Systems 93:101–114.

https://doi.org/10.1016/j.biosystems.2008.03.012
- Google Scholar
1. Boyden S
(1962) The chemotactic effect of mixtures of antibody and antigen on polymorphonuclear leucocytes
Journal of Experimental Medicine 115:453–466.

https://doi.org/10.1084/jem.115.3.453
- Google Scholar
1. Bray D
(1973)
Branching patterns of individual sympathetic neurons in culture

The Journal of Cell Biology 56:702–712.
- Google Scholar
1. Bray D
(1979)
Mechanical tension produced by nerve cells in tissue culture

Journal of Cell Science 37:391–410.
- Google Scholar
1. Bray D
(1984)
Axonal growth in response to experimentally applied mechanical tension

Developmental Biology 102:379–389.
- Google Scholar
(1994) A model of neurite extension across regions of nonpermissive substrate: simulations based on experimental measurement of growth cone motility and filopodial dynamics
Developmental Biology 163:407–422.

https://doi.org/10.1006/dbio.1994.1158
- Google Scholar
(1998)
Transport and turnover of microtubules in frog neurons depend on the pattern of axonal growth

The Journal of Neuroscience 18:821–829.
- Google Scholar
1. Chilton JK
(2006) Molecular mechanisms of axon guidance
Developmental Biology 292:13–24.

https://doi.org/10.1016/j.ydbio.2005.12.048
- Google Scholar
(2008)
Random walks models in biology

Journal of the Royal Society Interface 5:813–834.
- Google Scholar
(2007) Microfluidic engineered high cell density three-dimensional neural cultures
Journal of Neural Engineering 4:159–172.

https://doi.org/10.1088/1741-2560/4/2/015
- Google Scholar
(2001)
Generation of gradients having complex shapes using microfluidic networks

Analytical Chemistry 73:1240–1246.
- Google Scholar
1. Dickson BJ
(2002) Molecular mechanisms of axon guidance
Science 298:1959–1964.

https://doi.org/10.1126/science.1072165
- Google Scholar
(2010) GDNF acts as a chemoattractant to support ephrinA-induced repulsion of limb motor axons
Current Biology : CB 20:2150–2156.

https://doi.org/10.1016/j.cub.2010.11.021
- Google Scholar
1. Dudanova I
2. Kao TJ
3. Herrmann JE
4. Zheng B
5. Kania A
6. Klein R
(2012) Genetic evidence for a contribution of EphA:ephrinA reverse signaling to motor axon guidance
The Journal of Neuroscience 32:5209–5215.

https://doi.org/10.1523/JNEUROSCI.5707-11.2012
- Google Scholar
1. Dupin I
2. Dahan M
3. Studer V
(2013) Investigating axonal guidance with microdevice-based approaches
The Journal of Neuroscience 33:17647–17655.

https://doi.org/10.1523/JNEUROSCI.3277-13.2013
- Google Scholar
(2012) Calcium and cAMP levels interact to determine attraction versus repulsion in axon guidance
Neuron 74:490–503.

https://doi.org/10.1016/j.neuron.2012.02.035
- Google Scholar
1. Franze K
2. Guck J
(2010) The biophysics of neuronal growth
Reports on Progress in Physics 73:094601.

https://doi.org/10.1088/0034-4885/73/9/094601
- Google Scholar
1. Geschwind DH
2. Levitt P
(2007) Autism spectrum disorders: developmental disconnection syndromes
Current Opinion in Neurobiology 17:103–111.

https://doi.org/10.1016/j.conb.2007.01.009
- Google Scholar
(2004) Predicting axonal response to molecular gradients with a computational model of filopodial dynamics
Neural Computation 16:2221–2243.

https://doi.org/10.1162/0899766041941934
- Google Scholar
(1997) Cytomechanics of axonal development
Cell Biochemistry and Biophysics 27:135–155.

https://doi.org/10.1007/BF02738107
- Google Scholar
1. Hentschel HGE
2. Ooyen A. v.
(1999) Models of axon guidance and bundling during development
Proceedings of the Royal Society B: Biological Sciences 266:2231–2238.

https://doi.org/10.1098/rspb.1999.0913
- Google Scholar
(1999) Growth-cone attraction to netrin-1 is converted to repulsion by laminin-1
Nature 401:69–73.

https://doi.org/10.1038/43441
- Google Scholar
1. Kalil K
2. Li L
3. Hutchins BI
(2011) Signaling mechanisms in cortical axon growth, guidance, and branching
Frontiers in Neuroanatomy 5:62.

https://doi.org/10.3389/fnana.2011.00062
- Google Scholar
(1984)
Axonal elongation as a stochastic walk

Cell Motility 4:351–370.
- Google Scholar
1. Katz MJ
(1985)
How straight do axons grow?

The Journal of Neuroscience 5:589–595.
- Google Scholar
(2002) Regulation of substrate adhesion dynamics during cell motility
The International Journal of Biochemistry & Cell Biology 34:746–761.

https://doi.org/10.1016/S1357-2725(01)00171-6
- Google Scholar
1. Kent CB
2. Shimada T
3. Ferraro GB
4. Ritter B
5. Yam PT
6. McPherson PS
7. Charron F
8. Kennedy TE
9. Fournier AE
(2010) 14-3-3 proteins regulate protein kinase a activity to modulate growth cone turning responses
Journal of Neuroscience 30:14059–14067.

https://doi.org/10.1523/JNEUROSCI.3883-10.2010
- Google Scholar
1. Koch D
2. Rosoff WJ
3. Jiang J
4. Geller HM
5. Urbach JS
(2012) Strength in the periphery: growth cone biomechanics and substrate rigidity response in peripheral and central nervous system neurons
Biophysical Journal 102:452–460.

https://doi.org/10.1016/j.bpj.2011.12.025
- Google Scholar
1. Kolodkin AL
2. Tessier-Lavigne M
(2011) Mechanisms and molecules of neuronal wiring: a primer
Cold Spring Harbor Perspectives in Biology 3:a001727–14.

https://doi.org/10.1101/cshperspect.a001727
- Google Scholar
1. Krottje JK
2. van Ooyen A
(2007) A mathematical framework for modeling axon guidance
Bulletin of Mathematical Biology 69:3–31.

https://doi.org/10.1007/s11538-006-9142-4
- Google Scholar
(1989) Direct evidence that growth cones pull
Nature 340:159–162.

https://doi.org/10.1038/340159a0
- Google Scholar
1. Letourneau PC
(1978)
Chemotactic response of nerve fiber elongation to nerve growth factor

Developmental Biology 66:183–196.
- Google Scholar
Book
1. Letourneau PC
(2009)
Axonal pathfinding: Extracellular matrix role

In: Spire LR, editors. Encyclopedia of Neuroscience, vol 1. Oxford: Academic Press. pp. 1139–1145.
- Google Scholar
1. Li GH
2. QIn C
3. Wang LW
(1995)
Computer model of growth cone behavior and neuronal morphogenesis

Journal of Theoretical Biology 174:381–389.
- Google Scholar
(2009) Axon guidance and synaptic maintenance: preclinical markers for neurodegenerative disease and therapeutics
Trends in Neurosciences 32:142–149.

https://doi.org/10.1016/j.tins.2008.11.006
- Google Scholar
1. Lohof AM
2. Quillan M
3. Dan Y
4. Poo MM
(1992)
Asymmetric modulation of cytosolic cAMP activity induces growth cone turning

The Journal of Neuroscience 12:1253–1261.
- Google Scholar
1. López-Bendito G
2. Molnár Z
(2003) Thalamocortical development: how are we going to get there?
Nature Reviews. Neuroscience 4:276–289.

https://doi.org/10.1038/nrn1075
- Google Scholar
1. Lowery LA
2. Van Vactor D
(2009) The trip of the tip: understanding the growth cone machinery
Nature Reviews. Molecular Cell Biology 10:332–343.

https://doi.org/10.1038/nrm2679
- Google Scholar
1. Lu P
2. Tuszynski MH
(2008) Growth factors and combinatorial therapies for CNS regeneration
Experimental Neurology 209:313–320.

https://doi.org/10.1016/j.expneurol.2007.08.004
- Google Scholar
1. Lyuksyutova AI
2. Lu CC
3. Milanesio N
4. King LA
5. Guo N
6. Wang Y
7. Nathans J
8. Tessier-Lavigne M
9. Zou Y
(2003) Anterior-posterior guidance of commissural axons by wnt-frizzled signaling
Science 302:1984–1988.

https://doi.org/10.1126/science.1089610
- Google Scholar
(2004) Growth cone pathfinding: a competition between deterministic and stochastic events
BMC Neuroscience 5:22.

https://doi.org/10.1186/1471-2202-5-22
- Google Scholar
1. Millet LJ
2. Gillette MU
(2012) New perspectives on neuronal development via microfluidic environments
Trends in Neurosciences 35:752–761.

https://doi.org/10.1016/j.tins.2012.09.001
- Google Scholar
1. Ming GL
2. Wong ST
3. Henley J
4. Yuan XB
5. Song HJ
6. Spitzer NC
7. Poo MM
(2002) Adaptation in the chemotactic guidance of nerve growth cones
Nature 417:411–418.

https://doi.org/10.1038/nature745
- Google Scholar
1. Morel M
2. Shynkar V
3. Galas JC
4. Dupin I
5. Bouzigues C
6. Studer V
7. Dahan M
(2012) Amplification and temporal filtering during gradient sensing by nerve growth cones probed with a microfluidic assay
Biophysical Journal 103:1648–1656.

https://doi.org/10.1016/j.bpj.2012.08.040
- Google Scholar
(2008) Growth cone chemotaxis
Trends in Neurosciences 31:90–98.

https://doi.org/10.1016/j.tins.2007.11.008
- Google Scholar
1. Mortimer D
2. Pujic Z
3. Vaughan T
4. Thompson AW
5. Feldner J
6. Vetter I
7. Goodhill GJ
(2010) Axon guidance by growth-rate modulation
Proceedings of the National Academy of Sciences of the United States of America 107:5202–5207.

https://doi.org/10.1073/pnas.0909254107
- Google Scholar
1. Odde DJ
2. Buettner HM
(1995)
Time series characterization of simulated microtubule dynamics in the nerve growth cone

Annals of Biomedical Engineering 23:268–286.
- Google Scholar
1. Ohta H
2. Nishizuka M
3. Arai Y
4. Saito H
(1990)
Effect of nerve growth factor (nGF) on survival of superior cervical ganglion (sCG) transplanted into the third ventricle in rats japanese

Journal of Pharmacology 53:11–18.
- Google Scholar
(2008) A physical model of axonal elongation: force, viscosity, and adhesions govern the mode of outgrowth
Biophysical Journal 94:2610–2620.

https://doi.org/10.1529/biophysj.107.117424
- Google Scholar
(2011) Mathematical modeling of axonal formation. part i: geometry
Bulletin of Mathematical Biology 73:2837–2864.

https://doi.org/10.1007/s11538-011-9648-2
- Google Scholar
(2008) Analysis of the growth cone turning assay for studying axon guidance
Journal of Neuroscience Methods 170:220–228.

https://doi.org/10.1016/j.jneumeth.2008.01.014
- Google Scholar
(2009) Assays for eukaryotic cell chemotaxis
Combinatorial Chemistry & High Throughput Screening 12:580–588.

https://doi.org/10.2174/138620709788681952
- Google Scholar
(2010) Drosophila neurons actively regulate axonal tension in vivo
Biophysical Journal 99:3208–3215.

https://doi.org/10.1016/j.bpj.2010.09.029
- Google Scholar
1. Robles E
2. Gomez TM
(2006) Focal adhesion kinase signaling at sites of integrin-mediated adhesion controls axon pathfinding
Nature Neuroscience 9:1274–1283.

https://doi.org/10.1038/nn1762
- Google Scholar
(2004) A new chemotaxis assay shows the extreme sensitivity of axons to molecular gradients
Nature Neuroscience 7:678–682.

https://doi.org/10.1038/nn1259
- Google Scholar
1. Ruiz de Almodovar C
2. Fabre PJ
3. Knevels E
4. Coulon C
5. Segura I
6. Haddick PC
7. Aerts L
8. Delattin N
9. Strasser G
10. Oh WJ
11. Lange C
12. Vinckier S
13. Haigh J
14. Fouquet C
15. Gu C
16. Alitalo K
17. Castellani V
18. Tessier-Lavigne M
19. Chedotal A
20. Charron F
21. Carmeliet P
(2011) VEGF mediates commissural axon chemoattraction through its receptor Flk1
Neuron 70:966–978.

https://doi.org/10.1016/j.neuron.2011.04.014
- Google Scholar
(2013) A quantitative analysis of branching, growth cone turning, and directed growth in zebrafish retinotectal axon guidance
The Journal of Comparative Neurology 521:1409–1429.

https://doi.org/10.1002/cne.23248
- Google Scholar
1. Sloan TF
2. Qasaimeh MA
3. Juncker D
4. Yam PT
5. Charron F
(2015) Integration of shallow gradients of shh and netrin-1 guides commissural axons
PLoS Biology 13:e1002119.

https://doi.org/10.1371/journal.pbio.1002119
- Google Scholar
1. Song HJ
2. Ming GL
3. Poo MM
(1997) CAMP-induced switching in turning direction of nerve growth cones
Nature 388:275–279.

https://doi.org/10.1038/40864
- Google Scholar
1. Stoeckli ET
(2012) What does the developing brain tell us about neural diseases?
The European Journal of Neuroscience 35:1811–1817.

https://doi.org/10.1111/j.1460-9568.2012.08171.x
- Google Scholar
1. Suter DM
2. Miller KE
(2011) The emerging role of forces in axonal elongation
Progress in Neurobiology 94:91–101.

https://doi.org/10.1016/j.pneurobio.2011.04.002
- Google Scholar
(2015) Passive microfluidic chamber for long-term imaging of axon guidance in response to soluble gradients
Lab on a Chip 15:2781–2789.

https://doi.org/10.1039/c5lc00503e
- Google Scholar
1. Tessier-Lavigne M
2. Goodman CS
(1996)
The molecular biology of axon guidance

Science 274:1123–1133.
- Google Scholar
(2011) Cyclic nucleotide-dependent switching of mammalian axon guidance depends on gradient steepness
Molecular and Cellular Neurosciences 47:45–52.

https://doi.org/10.1016/j.mcn.2011.02.012
- Google Scholar
(2013) Measurement of tension release during laser induced axon lesion to evaluate axonal adhesion to the substrate at piconewton and millisecond resolution
Journal of Visualized Experiments 75:50477.

https://doi.org/10.3791/50477
- Google Scholar
1. Verge VM
2. Merlio JP
3. Grondin J
4. Ernfors P
5. Persson H
6. Riopelle RJ
7. Hökfelt T
8. Richardson PM
(1992)
Colocalization of NGF binding sites, trk mRNA, and low-affinity NGF receptor mRNA in primary sensory neurons: responses to injury and infusion of NGF

The Journal of Neuroscience 12:4011–4022.
- Google Scholar
1. Wang JC
2. Li X
3. Lin B
4. Shim S
5. Ming GL
6. Levchenko A
(2008)
A microfluidics-based turning assay reveals complex growth cone responses to integrated gradientsof substrate-bound ECM molecules and diffusible guidance cues

Lab Chip 586:227–237.
- Google Scholar
1. Wehrman T
2. He X
3. Raab B
4. Dukipatti A
5. Blau H
6. Garcia KC
(2007) Structural and mechanistic insights into nerve growth factor interactions with the TrkA and p75 receptors
Neuron 53:25–38.

https://doi.org/10.1016/j.neuron.2006.09.034
- Google Scholar
1. Wetmore C
2. Olson L
(1995) Neuronal and nonneuronal expression of neurotrophins and their receptors in sensory and sympathetic ganglia suggest new intercellular trophic interactions
The Journal of Comparative Neurology 353:143–159.

https://doi.org/10.1002/cne.903530113
- Google Scholar
1. Whitesides GM
(2006) The origins and the future of microfluidics
Nature 442:368–373.

https://doi.org/10.1038/nature05058
- Google Scholar
1. Xiang Y
2. Li Y
3. Zhang Z
4. Cui K
5. Wang S
6. Yuan Xiao-bing
7. Wu Chien-ping
8. Poo Mu-ming
9. Duan S
(2002) Nerve growth cone guidance mediated by g protein–coupled receptors
Nature Neuroscience 5:843–848.

https://doi.org/10.1038/nn899
- Google Scholar
1. Xu J
2. Rosoff WJ
3. Urbach JS
4. Goodhill GJ
(2005) Adaptation is not required to explain the long-term response of axons to molecular gradients
Development 132:4545–4552.

https://doi.org/10.1242/dev.02029
- Google Scholar
1. Yam PT
2. Langlois SD
3. Morin S
4. Charron F
(2009) Sonic hedgehog guides axons through a noncanonical, src-family-kinase-dependent signaling pathway
Neuron 62:349–362.

https://doi.org/10.1016/j.neuron.2009.03.022
- Google Scholar
1. Yaron A
2. Zheng B
(2007) Navigating their way to the clinic: emerging roles for axon guidance molecules in neurological disorders and injury
Developmental Neurobiology 67:1216–1231.

https://doi.org/10.1002/dneu.20512
- Google Scholar
(1991)
Tensile regulation of axonal elongation and initiation

The Journal of Neuroscience 11:1117–1125.
- Google Scholar
1. Zicha D
2. Dunn GA
3. Brown AF
(1991)
A new direct-viewing chemotaxis chamber

Journal of Cell Science 4:769–775.
- Google Scholar
1. Zigmond SH
(1977)
Ability of polymorphonuclear leukocytes to orient in gradients of chemotactic factors

The Journal of Cell Biology 75:606–616.
- Google Scholar

Article and author information

Author details

Huyen Nguyen
1. Queensland Brain Institute, The University of Queensland, St. Lucia, Australia
2. School of Mathematics and Physics, The University of Queensland, St. Lucia, Australia
Contribution
HN, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article

Competing interests
The authors declare that no competing interests exist.

"This ORCID iD identifies the author of this article:" 0000-0002-5775-7915
Peter Dayan

Gatsby Computational Neuroscience Unit, University College London, London, United Kingdom

Contribution
PD, Conception and design, Analysis and interpretation of data, Drafting or revising the article

Competing interests
The authors declare that no competing interests exist.

"This ORCID iD identifies the author of this article:" 0000-0003-3476-1839
Zac Pujic

Queensland Brain Institute, The University of Queensland, St. Lucia, Australia

Contribution
ZP, Conception and design, Acquisition of data, Analysis and interpretation of data, Drafting or revising the article

Competing interests
The authors declare that no competing interests exist.
Justin Cooper-White

Australian Institute for Bioengineering and Nanotechnology, The University of Queensland, St. Lucia, Australia

Contribution
JCW, Conception and design, Analysis and interpretation of data, Drafting or revising the article

Competing interests
The authors declare that no competing interests exist.
Geoffrey J Goodhill
1. Queensland Brain Institute, The University of Queensland, St. Lucia, Australia
2. School of Mathematics and Physics, The University of Queensland, St. Lucia, Australia
Contribution
GJG, Conception and design, Analysis and interpretation of data, Drafting or revising the article

For correspondence
g.goodhill@uq.edu.au

Competing interests
The authors declare that no competing interests exist.

"This ORCID iD identifies the author of this article:" 0000-0001-9789-9355

Funding

National Health and Medical Research Council (1083707)

Geoffrey J Goodhill

Gatsby Charitable Foundation

Peter Dayan

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Ethics

Animal experimentation: Experiments involving animals were conducted in accordance with the Animal Care and Protection Act Qld (2002) and the Australian Code of Practivce for the Care and Use of Animals for Scientific Purposes, 7th edition (2004). Ethics approval was obtained from The University of Queensland Ethics Committee, approval number AE02608.

Copyright

This article is distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use and redistribution provided that the original author and source are credited.