The size of the EB cap determines instantaneous microtubule stability
- The Francis Crick Institute, United Kingdom
- London Centre of Nanotechnology, United Kingdom
Figures
Figure 1 with 2 supplements
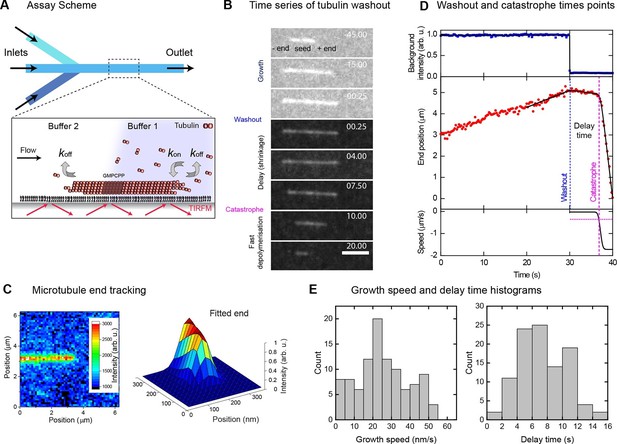
Momentary microtubule stability assayed by fast tubulin washout and nm precision plus end tracking.
(A) Schematic of the microfluidic TIRF microscopy setup. (B) TIRF microscopy image sequence of an Alexa568-microtubule before and after washout, with growth, delay and fast depolymerisation periods indicated. Tubulin concentration was changed from 20 to 0 μM at washout. Time in seconds, scale bar is 3 µm. (C) Illustration of sub-pixel precision microtubule end tracking using a 2D fitting procedure (Materials and methods, [Bohner et al., 2015]). (D) Plots of the background fluorescence intensity (top) and end position data (middle) of a washout experiment together with the fits (solid black lines) used to extract the derived parameter values (see Materials and methods). (E) Histograms of the growth speeds at tubulin washout (left) and of the subsequent delay times before catastrophe (right) (n = 101).
Figure 1—figure supplement 1
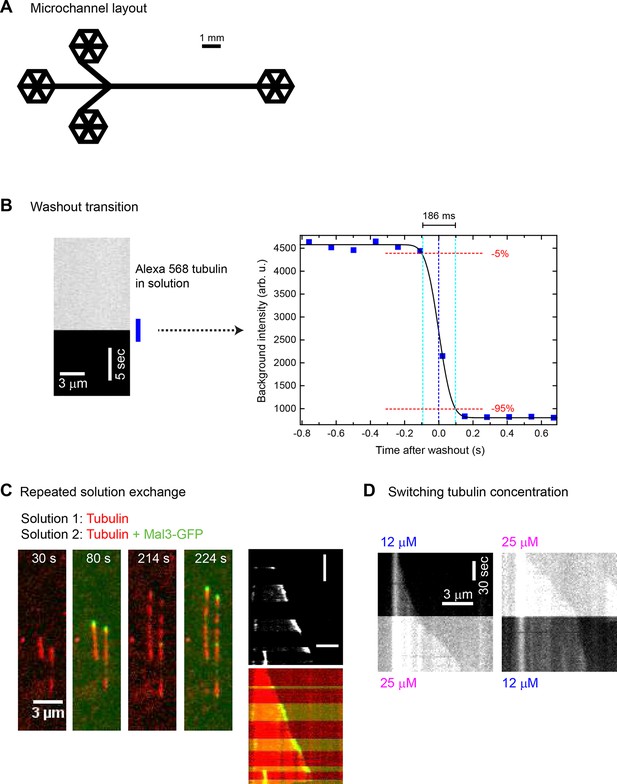
Fast and complete microfluidics-controlled solution exchange.
(A) Scaled layout of microfluidic channels used in this study. The channel width was 300 µm and the height was 95 ± 5 µm. (B) Representative kymograph (left) and a plot of the time course (right) of 20 µM Alexa568-tubulin (12.5% labelled; 2.5 µM in total) fluorescence intensity as measured by TIRF microscopy, showing fast and complete solution exchange (imaged at 7.7 Hz): from 9 experiments, the average time for 90% buffer exchange (5% - 95%) was 199 (± 32 s.e.m) ms. (C) Left: Time series of TIRF microscopy images showing microtubules (red) growing from a surface-immobilised seed during repeated sudden microfluidics-controlled exchanges between solutions containing 75 nM Mal3-GFP (green) and not containing any Mal3-GFP, in the constant presence of 15 µM Alexa568-tubulin. Right: a corresponding kymograph (top: GFP channel only, bottom: merge). Horizontal and vertical scale bars are 3 µm and 1 min, respectively. Persistent microtubule growth is not affected by solution exchanges. Time in seconds, recording frequency was 0.5 Hz. (D) Kymographs showing a Alexa568-microtubule growing from an immobilised seed; the growth speed changes abruptly in response to a sudden microfluidics-controlled change of the Alexa568-tubulin concentration from 12 μM to 25 μM (left) or from 25 μM to 12 μM (right), again demonstrating that solution exchange does not cause catastrophes
Figure 1—figure supplement 2
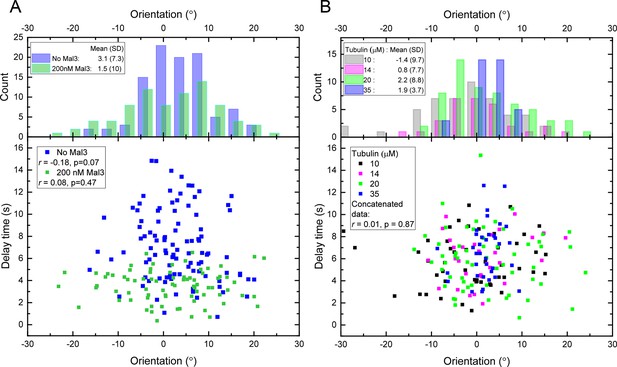
Delay times and microtubule orientations.
(A) Top: distribution of individual microtubule orientations, each averaged over 10 s growth before tubulin washout, for the conditions without Mal3 (Figures 1, 2) and with 200 nM Mal3-GFP (Figures 3, 4). The microchannel axis is 0° and corresponds to the flow direction. Bottom: Delay times after washout versus orientation before washout, for the individual microtubules shown in the top panel. (B) As (A) for the tubulin concentration variation datasets (Figure 6A). For each dataset, the Pearson’s r correlation coefficients were calculated using the magnitude of the orientations relative to the distribution mean.
Figure 2 with 1 supplement
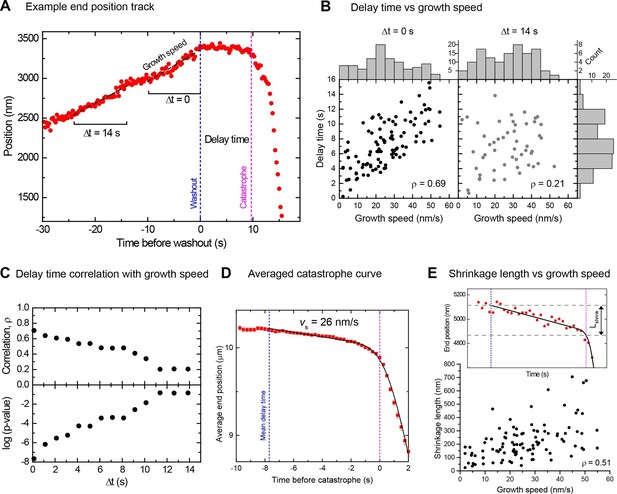
Momentary stability increases with growth speed at washout time.
(A) Example end position-time plot. Growth speeds were measured by linear fits over a 10 s time window directly before washout (Δt = 0) or for comparison also at earlier times up to 14 s before washout. (B) Scatter plots showing a positive correlation between delay times and growth speeds when measured directly before washout (Δt = 0); correlation strength (Spearman's rank correlation coefficient ρ) is significantly reduced for Δt = 14 s. Histograms of growth speeds (top) and delay times (right) are also shown. (C) Spearman's rank correlation coefficient ρ (top) and corresponding p-values (below) between delay time and growth speed indicate that the correlation strength decreases progressively when the time window over which speed is determined is shifted away from the washout time point. (D) Averaged microtubule end position trace after washout (alignment with respect to catastrophe times). Errors are s.e.m. (E) Top: Example trace of a shrinkage episode for an individual microtubule after washout, with fit (Materials and methods) illustrating the definition of shrinkage length. Blue and magenta lines indicate washout and catastrophe times, respectively. Bottom: scatter plot of the shrinkage lengths versus growth speeds.
Figure 2—figure supplement 1
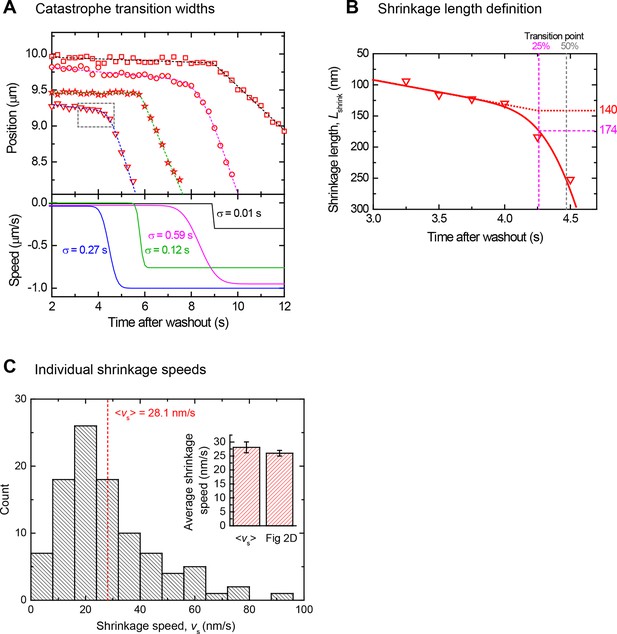
Determination of catastrophe and shrinkage parameters after tubulin washout.
(A) Top: End position - time plots showing four example catastrophes (offset in position) from the data set in Figure 2, with fits as described in the Materials and methods (dashed lines). Bottom: corresponding speeds and transition widths, σ, determined from the fits above. Good fits are produced for the end position traces for a large range of transitions between slow shrinkage to fast depolymerisation at catastrophe. (B) Enlarged view of a catastrophe transition (dashed box in panel A, illustrating the definitions of the shrinkage length between washout and catastrophe used in the text: the time point of 25% change in speed is defined as the catastrophe time (magenta dashed lines). The difference in microtubule end position between the washout time and the catastrophe time is defined as the measured shrinkage length (here 174 nm). In contrast, for simplicity the predicted shrinkage length (here 140 nm) is obtained from an extrapolated linear fit to the slow shrinkage episode between washout and catastrophe. For gradual transitions between slow shrinkage to fast depolymerisation, the predicted shrinkage length is systematically a few tens percent shorter than the measured shrinkage length, but nevertheless provides a good estimate of the range of lengths. (C) Distribution of individual shrinkage speeds after washout. Histogram of slow shrinkage speeds after washout as determined from a linear fit to the end position trace between tubulin washout and catastrophe, corresponding to the data set in Figure 2. The mean shrinkage speed obtained from a fit to the average when all tracks are aligned at the catastrophe time point (Figure 2D) is very similar to the mean speed from fits to all individual shrinking phases (bar graph, inset).
Figure 3
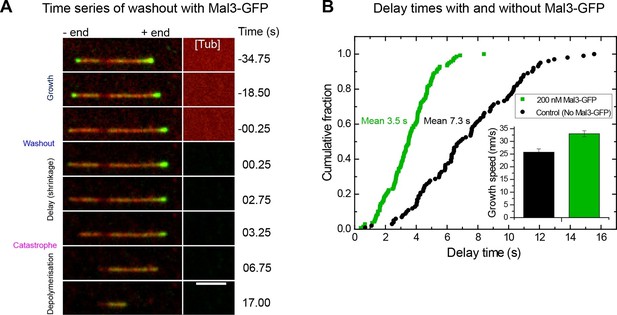
Mal3 shortens the delay between tubulin washout and catastrophe.
(A) TIRF microscopy image sequence of a Alexa568-microtubule (red) in a tubulin washout experiment in the constant presence of 200 nM Mal3-GFP (green). Tubulin was present at 20 µM before washout. Background has been subtracted; the raw background intensity of the tubulin/microtubule channel is depicted on the right hand side ([Tub]), indicating when tubulin is removed; other conditions are as in Figures 1 and 2. Time in seconds, scale bar is 3 µm. (B) Cumulative delay time distributions in the presence of 200 nM Mal3-GFP (green) and in its absence (black). Inset: bar graph of the corresponding mean growth velocities before washout; error bars are s.e.m.
Figure 4 with 2 supplements
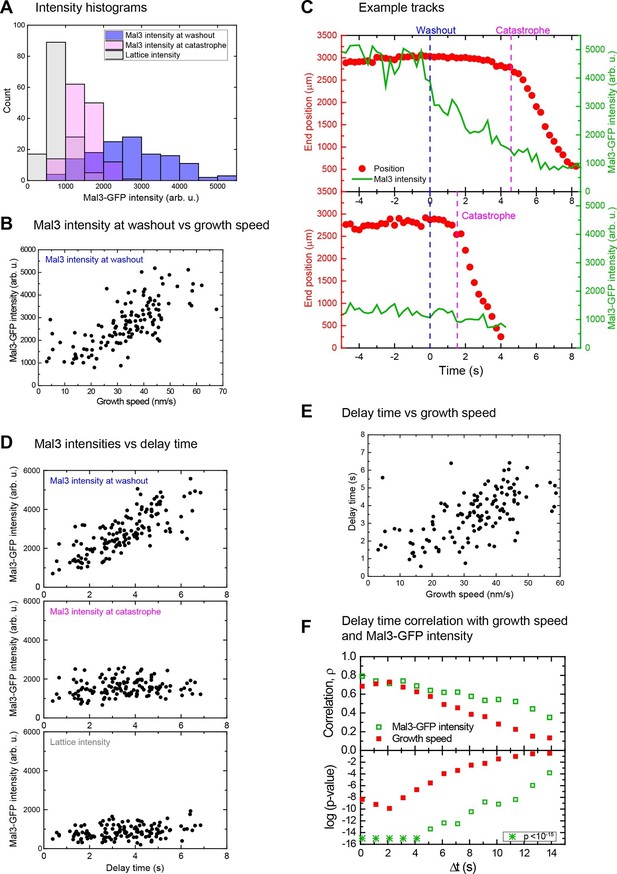
Microtubules with longer EB site caps are more stable.
(A) Histograms of the Mal3-GFP intensity at microtubule ends at the moment of tubulin washout (blue) and catastrophe (magenta) (n = 139). The corresponding lattice intensity at tubulin washout (grey) is also shown. Mal3-GFP was present at 200 nM throughout the experiment and tubulin at 20 µM before washout. (B). Scatter plot showing the positive correlation of Mal3-GFP intensities and growth speeds determined directly before washout. (C) Two representative end position time plots (red dots) with the corresponding Mal3-GFP signals (green line). The microtubule with an initially stronger Mal3-GFP signal at washout (top) has a longer delay time until catastrophe compared to the microtubule with weaker Mal3-GFP signal at washout (bottom). (D) Scatter plots of Mal3-GFP intensities at microtubule ends at the time of tubulin washout (top), at microtubule ends at the time of catastrophe (middle), and on the microtubule lattice (1.5 µm from the microtubule end) (bottom) versus the delay times. At the moment of catastrophe, on average 29% of the EB binding sites present at tubulin washout were left, calculated by comparing the Mal3-GFP intensity at washout and catastrophe, from each of which the lattice intensity was subtracted. (E) Scatter plot showing the positive correlation of delay times and growth speeds determined directly before washout. Delay times were independent of small variations of the microtubule orientation (Figure 1—figure supplement 2A, green data). (F) Decrease of correlation strength ρ between Mal3-GFP intensities and delay times (open green symbols) or growth speeds and delay times (solid red symbols) when the intensities/speeds were measured at earlier time points before washout, similar to Figure 2. Spearman's rank correlation coefficients ρ (top) and corresponding p-values (bottom, log scaled) are depicted.
Figure 4—figure supplement 1
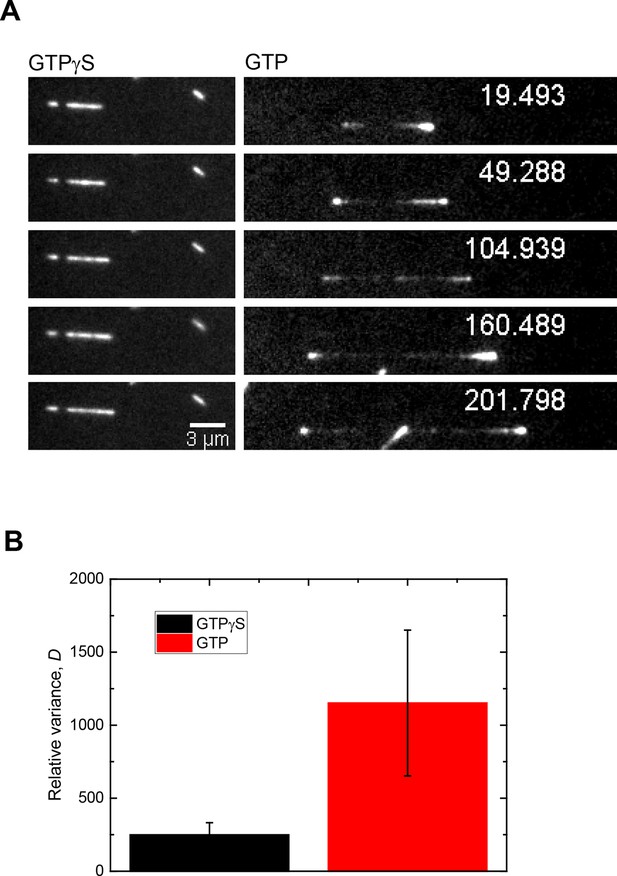
The main source of Mal3-GFP intensity fluctuations at microtubule ends growing in the presence of GTP are fluctuations of the size of the EB binding site cap.
(A) Time series of TIRF microscopy images (GFP channel only) of 75 nM Mal3-GFP binding to microtubules growing in the presence of either GTPγS (left) or GTP (right). GTPγS is a slowly hydrolysable GTP or GDP-Pi analogue, transforming the entire microtubule into a mimic of a microtubule end with a constant density of EB binding sites (Maurer et al., 2011). Tubulin concentration was 22 µM. Time is in seconds, the frame rate was 9.9 Hz. (B) Bar graph showing the relative variance, D, (see Materials and methods) of Mal3-GFP intensities at growing microtubule end for the conditions in A. Error bars are standard deviations. For each condition, 15,000 image frames were analyzed. Because the EB binding site density on GTPγS microtubules is maximal and constant, the larger relative variance measured at microtubule ends growing in the presence of GTP demonstrates that the broad distribution of Mal3-GFP intensities under this condition (data set in Figure 4) is largely due to the variability of the number of high affinity EB binding sites at growing microtubule ends and not to stochastic binding/unbinding events or measurement noise. Therefore, the measured Mal3-GFP intensities at growing microtubule ends are a good measure for the size of the EB binding region.
Figure 4—figure supplement 2
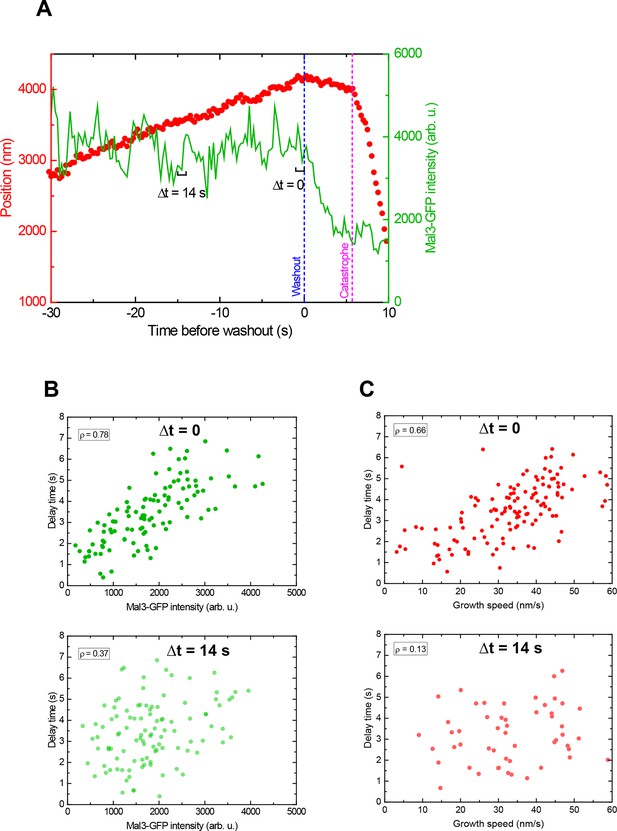
The instant EB cap length defines momentary stability.
(A) Example plot of a tubulin washout track with the microtubule end position in red and the corresponding Mal3-GFP intensity in green, from the data set in Figure 4. Mal3-GFP intensities were measured over time windows of 1 s, which were successively shifted away from the washout time point: (B) the intensity at Δt = 0 (directly before washout) shows a strong positive correlation with the delay time (top), which decreases at larger shifts (bottom Δt = 14 s). (C) The correlation between growth speed and delay time shows a similar trend with increasing shift, also consistent with the data presented in in Figure 2 in the absence of Mal3-GFP. The data in B top and C top are the same as in Figure 4D top and E. These data demonstrate that both the instantaneous EB cap length and growth speed are indicative of the 'momentary' stability of the microtubule.
Figure 5
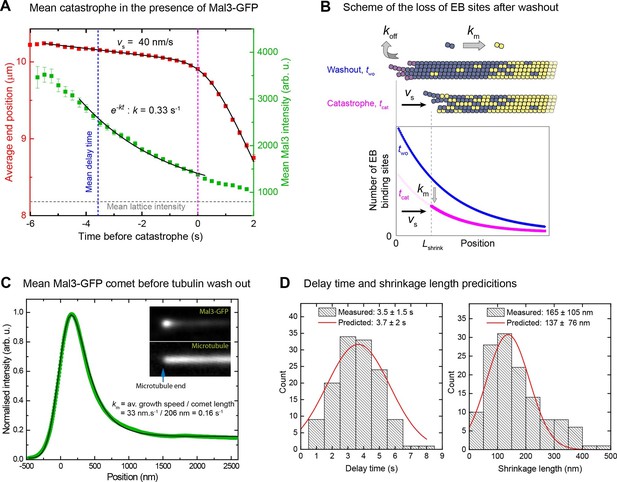
When an EB cap size threshold is reached catastrophe is induced.
(A) Averaged microtubule end position traces (red) and Mal3-GFP intensity traces (green) after tubulin washout (alignment with respect to the catastrophe time), and fits (black lines) (Materials and methods). Same data set as in Figure 4. (B) Top: Scheme illustrating the two processes leading to EB cap loss after tubulin washout: disassociation of tubulin from the end (koff) resulting in slow shrinkage (vs), and maturation of EB binding sites into mature lattice (km). Together these processes define the kinetics of the decay of EB binding sites (Materials and methods). Bottom: simple model of average distributions of the EB binding sites at washout (two) and catastrophe (tcat) times. (C) Comet analysis: Average (green) of 5500 Mal3-GFP intensity profiles aligned with respect to the microtubule end position as described in (Maurer et al., 2014) and a fit to the data (black) yielding the comet length, which together with the growth velocity provides the maturation rate (Materials and methods). (D) Histograms of the distribution of measured delay times (left) and shrinkage lengths (right) overlaid with theoretical estimates (red solid line) from an empirical kinetic model (Materials and methods) based on the measured GFP intensity distributions (Figure 4A) and the measured kinetic parameters from panel A and C.
Figure 6 with 3 supplements
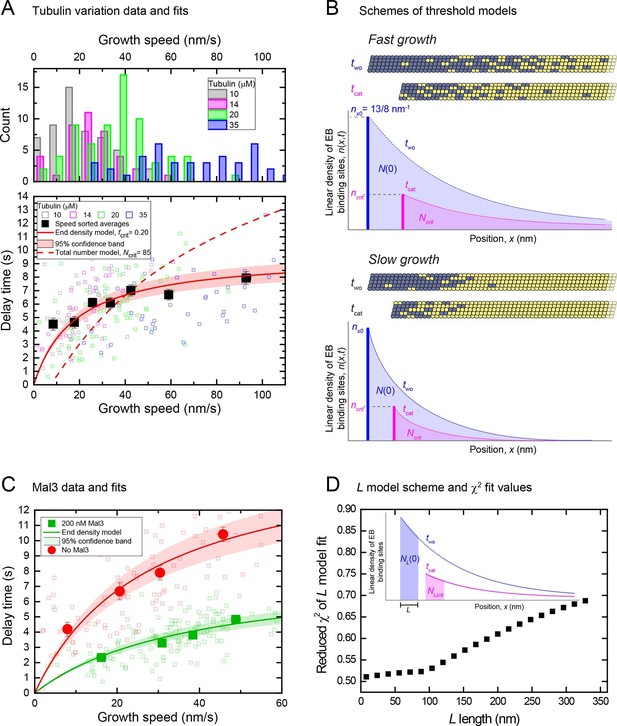
An end density threshold explains the dependence of the mean delay times on growth speed.
(A) Top: Histograms of overlapping growth speed distributions at tubulin washout for 10, 14, 20 and 35 μM tubulin. Bottom: Scatter plots of the corresponding individual delay times versus growth speeds (open symbols) and of the averages for 7 different speed groups (filled symbols) (see Figure 6—figure supplement 1A). Error bars are s.e.m. n = 210. Fits are shown for kinetic models assuming that catastrophe is induced when either a critical EB binding site density in the end region (solid line, Equation 11 in Materials and methods) or a critical total number of EB sites (dashed line, Equation 13 in Supplemental Materials and methods) is reached (Materials and methods). As for the other datasets, delay times were independent of small variations of the microtubule orientation (Figure 1—figure supplement 2B). (B) Schemes illustrating the two threshold scenarios for a fast (top) and slowly (bottom) growing microtubule. The total number of EB binding sites (shaded areas under the curves) is different for the two speeds when the same critical end density of sites (bold vertical lines indicating the maximum amplitude of the curves) has been reached. This illustrates that the threshold values of a kinetic model assuming a critical 'end density' threshold and of a model assuming a critical 'total number' threshold have different dependencies on the initial length of the EB binding region before tubulin washout. This leads to different predictions of the dependence of the delay times on the growth speed as shown in (A). (C) Scatter plots of the data previously shown in Figure 2B left and Figure 4—figure supplement 2C top, without and with Mal3-GFP (green and red symbols, respectively): individual delay times versus growth speeds (open symbols) and of the averages for 4 different speed groups (filled symbols). Error bars are s.e.m. Solid lines are fits to the data using the end density threshold model (Equation 11 in Materials and methods). The delay times of the data without Mal3 differ slightly from those shown in (A) as a consequence of different Mg concentrations. (D) Global fits to the speed-sorted data in A, C and the speed-sorted Mal3-GFP intensities at tubulin washout and catastrophe (from Figure 4D top and middle) using the L- model that considers as a threshold the number of EB cap sites within a region of length L behind the microtubule end. Reduced χ2 values are shown for a range of L values. Example fits at L = 8 nm, 80 nm and 320 nm are shown in Figure 6—figure supplement 2. Inset: Scheme showing the region considered in the L model and the number of EB sites within that region (Materials and methods).
Figure 6—figure supplement 1
Growth and shrinkage speeds and delay times of the data sets with varied tubulin concentrations.
(A) Illustration of speed-sorting: Histogram showing all growth speeds from the 4 data sets with different tubulin concentrations presented in Figure 6A. The data was then sorted into 7 groups each containing 31 microtubules, according to their measured speed before washout, irrespective of the original tubulin concentration. (B) Delay times as a function of tubulin concentration: box plots depicting the delay times of microtubules grown at different tubulin concentrations. Same data set as in Figure 6A. (C) Scatter plot of the slow shrinkage speed vs after washout against the growth speed vg before washout. A mild correlation was observed; the explicit relationship between vs and vg was necessary for the model fits to the experimental data in Figure 6A and Figure 6—figure supplement 2. This observation potentially supports earlier proposals that predict higher koff rates for faster and more tapered microtubule ends (Coombes et al., 2013; Gardner et al., 2011a).
Figure 6—figure supplement 2
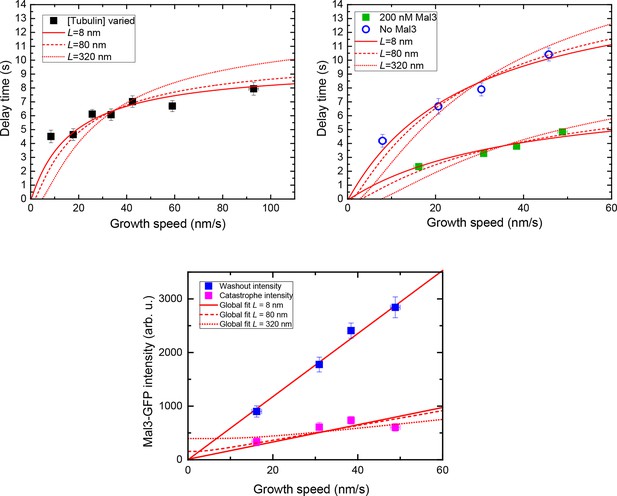
Threshold model fits considering the number of binding sites within a specific length, L.
Simultaneous fits to the delay times of the tubulin concentration variation data (left, top) in Figure 6A, the delay times of the data with and without Mal3-GFP (right, top) in Figure 6C, and speed-sorted and background-subtracted Mal3-GFP intensity data (bottom) from Figure 4D, using the L model shown in Figure 6D (Equation 17–19). Solid, dashed and dotted lines are for L = 8, 80, and 320 nm, respectively, supporting the idea that the front part of the cap – and not its entirety – is important for stability.
Figure 6—figure supplement 3
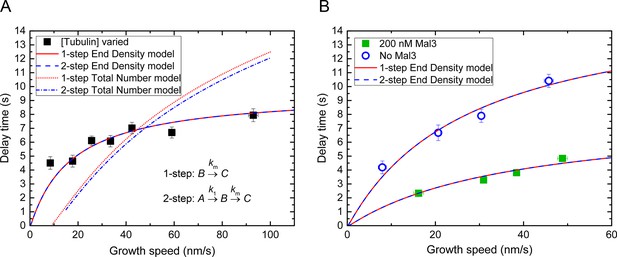
Threshold model fits considering 2-step maturation of the microtubule end.
(A) Averaged delay times as a function of microtubule growth speed as shown in Figure 6A (tubulin concentration variation dataset) are fitted using either an 'end density' or 'total number' threshold model, either assuming simple 1-step maturation of microtubule end regions, as throughout this study, or assuming 2-step maturation kinetics (Maurer et al., 2014), as indicated. Both end density models yield good fits, predicting thresholds of 0.20 and 0.25 for the 1-step and 2-step maturation model, respectively. Both 'total number' models yielded unsatisfactory fits. (B) Averaged delay times as shown in Figure 6C (Mal3 dataset and its control) are fitted using an 'end density' threshold model either assuming 1-step or 2-step microtubule end maturation, as indicated. Predicted thresholds: Mal3 data – 0.28 and 0.29 for the 1-step and 2-step model, respectively; control without Mal3 – 0.14 and 0.17 for the 1-step and 2-step model, respectively. For the fits of the data without Mal3, k1 = 5km; for the fits of the data with Mal3, k1 = 20km (Maurer et al., 2014). The other fit parameters were as in Figure 6A and 6C.
Author response image 1
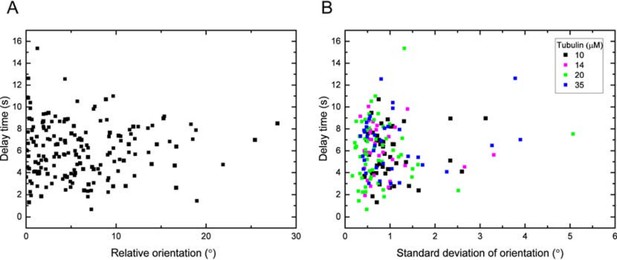
(A) Delay time vs. the magnitude of the orientation of the data in Figure 1—figure supplement 2B relative to the mean: for each data point of a specific tubulin concentration, the mean of the distribution has been subtracted and the magnitude of this relative orientation is plotted.
Statistical analysis shows no significant correlation (Pearson’s r =0.01). (B) Delay time vs. the standard deviation of the growth orientation measured over 10s before washout. Statistical analysis shows no significant correlation (Pearson’s r =0.1, p = 0.17).
Videos
Video 1
Tubulin washout experiment, corresponding to Figure 1.
A drop in background fluorescence marks the time point, when tubulin is removed. Microtubules undergo catastrophe with a delay. Time is in seconds, where 0 is set to the washout time point.
Video 2
Tubulin washout experiment in the presence of 200 nM Mal3-GFP (yellow), corresponding to Figure 3.
Microtubules are depicted in blue. The microtubule with the higher Mal3-GFP signal at the time point of washout exhibits a longer delay until catastrophe occurs. Time is in seconds, where 0 is set to the washout time point. To enhance clarity of presentation, background subtraction (imageJ, 30 pixel rolling ball plug-in) was applied to suppress the large difference between total intensities in the microtubule channel before and after washout.
Additional files
-
Supplementary file 1
(A) Fit parameters from analysis of comet profiles.
(B) Fit parameters for the various different threshold models. (C) Correlations between measured parameters.
- https://doi.org/10.7554/eLife.13470.019
-
Supplementary file 2
Numerical values for the data presented in Figures 4, 6A and C.
- https://doi.org/10.7554/eLife.13470.020
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
The size of the EB cap determines instantaneous microtubule stability
eLife 5:e13470.
https://doi.org/10.7554/eLife.13470
