Figures and data in Continuous lateral oscillations as a core mechanism for taxis in Drosophila larvae | eLife

Figures
Tables

9 figures and 1 table

Figures

Figure 1 with 1 supplement

Download asset Open asset

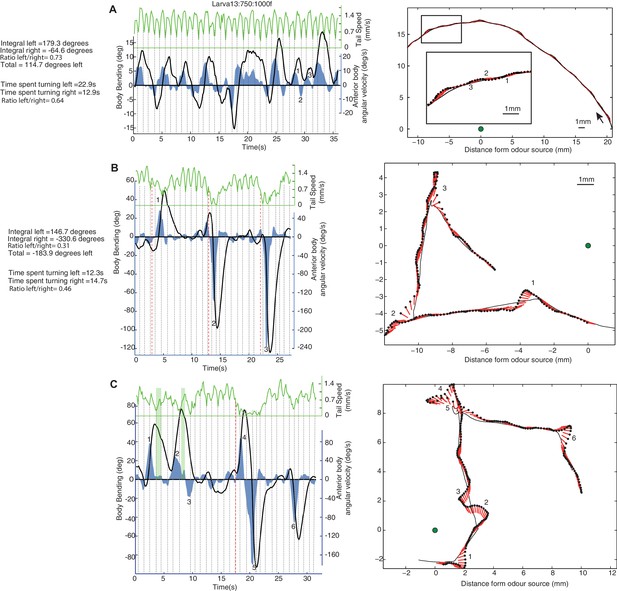
Examples of individual larva motion dynamics during chemotaxis show lateral oscillations.

Left side panels show the angular speed of the anterior part of the body (blue), body bending (black), and peristaltic steps (grey dotted lines) based on tail speed (green) corresponding to the paths shown on the right. Events of interest are labeled by numbers. (A) Path section with no peristalsis inhibition. The larva shows a continuous alternation between left and right, but turning is biased in both amplitude and duration towards positive angles, resulting in a left curve. (B) Path section with an intermediate (1) and two stronger (2 and 3) peristalsis inhibition events that do not interrupt the turning alternation. (C) Path section with a peristalsis inhibition event covering two successive turns (4 and 5). The green vertical bars (1 and 2) indicate moments at which the body bending decreases (from left to right) even though the larva anterior body is still slightly swinging towards the left. This is due to the simultaneous forward peristalsis motion bringing the posterior part of the body towards the axis of the anterior part. The angular speed of the anterior body provides thus a better proxy than body bend to infer the control commands involved. (B,C) Red dotted lines indicate the onset of peristalsis inhibition (conservatively late measure) which occurs before any strong changes in angular speed or body bending.

https://doi.org/10.7554/eLife.15504.002

Figure 1—figure supplement 1

Download asset Open asset

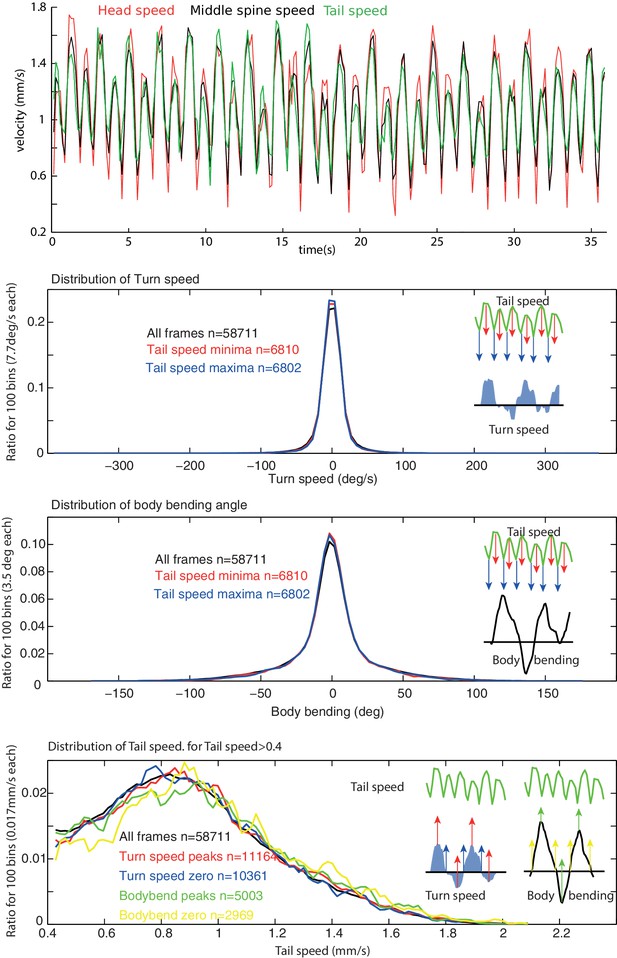
Peristalsis and lateral oscillation rhythms appear decoupled.

(A) During forward crawling, the speed of the tail, middle spine point and head show a strongly correlated rhythm characteristic of the peristalsis motion (note that some individuals display a continuous alternation between a strong and a weak step). We used tail speed to characterise peristalsis motion as it is the least sensitive to the lateral motion of the anterior body. (B,C) Anterior body angular velocity and, to a lesser extent body bending, are representative of the rhythmic activity of the continuous lateral oscillations displayed by the larva (see Figure 3). However, the distribution of anterior body angular velocities (B); and body bending angles (C) is similar whether sampled across all frames or during specific phases of the peristalsis rhythm, such as peaks of tail speed. (D) Similarly, the distribution of tail speed during forward motion (tail speed < 0.4) is similar whether sampled across all frames or during specific phases of the anterior body angular velocity and body bending activities. Together with the fact the mean frequencies of the two rhythms are not harmonics (Figure 3D), this suggests that that the peristalsis and lateral oscillation rhythms are generated independently.

https://doi.org/10.7554/eLife.15504.003

Figure 2 with 1 supplement

Download asset Open asset

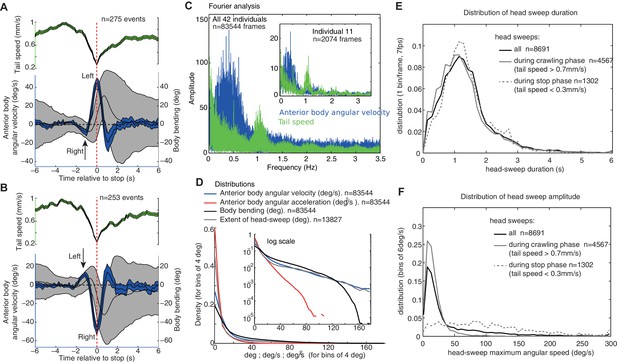
Group statistics of larva motion dynamics during chemotaxis support the existence of an intrinsic lateral oscillatory rhythm.

(A,B) Average (±95%CI) dynamics of the anterior body angular velocity (blue), body bending (black) and tail velocities (green) displayed before and after the onset of peristalsis inhibition events aligned at $t = 0$ (dashed red line, when tail speed drops to a minimum), and categorised according to whether the larva is sweeping towards the left (A) or right (B) at $t = 0$ . Drops in forward crawling speed tend to be accompanied by a large head sweep, as shown previously (Hernandez-Nunez et al., 2015) (see Figure 2—figure supplement 1). Large head sweeps are preceded by low-amplitude head casts in the opposite direction (arrows), suggesting the large head cast direction is dependent on the state of the oscillation. (C) Fourier analysis of the angular velocity of the anterior body (blue) and tail speed (green) across all larvae (see inset for a single individual). Tail speed (peristalsis) rhythm is fairly constant across larvae at around 1.0 Hz, with slight harmonics of the tail speed at 0.5 Hz, which results from the tendency of some larvae to alternate continuously between a weaker and stronger peristalsis wave (see Figure 1A's tail speed for an example). The angular velocity of the anterior body (blue) shows a slower rhythm than the peristalsis, with a higher variation across and within individuals. Note that the rhythms are not multiples of each other, suggesting that they are operating independently (see also Figure 1—figure supplement 1). (D) Distributions of markers of the anterior body sweeps (see inset for logarithmic scale) reveal no sign of bimodality, suggesting a continuum of turning modulations rather than the triggering of distinct specific actions. (E,F) Distributions of individual head-sweep’s duration (E) and maximum angular speed (F). Head sweeps are defined as the period between the two successive points in time where the anterior body angular speed crosses zero. (F) Head sweeps tend to reach higher angular velocity during stop phases (dash grey) than during crawling phases (grey) (i.e. when tail speed average during head sweep is <0.3 mm/s and >0.7 mm/s, respectively). (E) Head sweep durations can vary; however, the distributions of duration are similar during stop phases (dash grey) and forward crawling phases (grey), suggesting a shared underlying oscillatory rhythm (E).

https://doi.org/10.7554/eLife.15504.004

Figure 2—figure supplement 1

Download asset Open asset

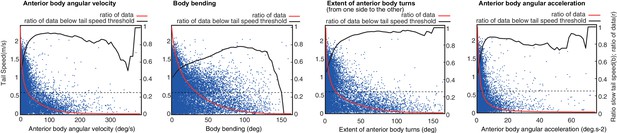
Correlation of head sweep statistics to tail speed.

Head sweep statistics [from left to right: anterior body angular velocity; body bending; extent of anterior body turns (i.e. angular extent from one side to the other) and anterior body angular acceleration] are plotted against tail speed for a random selection of points across all larvae track (blue). Full red line shows the ratio of data that are higher than the current $x$ value. Black line shows the ratio of such data (higher than current $x$ value) that are below the tail speed threshold (black dash line). Tail speed below the threshold is considered as a proxy for peristalsis inhibition. Peristalsis inhibition correlates well with high head-sweep velocity, acceleration, and angular extent. However, large body-bending is a less powerful predictor of peristalsis inhibition. This suggests that peristalsis inhibition is not a mere physical consequence of large body bending. Rather, peristalsis inhibition seems controlled by a signal sent simultaneously to the signal modulating lateral oscillations.

https://doi.org/10.7554/eLife.15504.005

Figure 3 with 1 supplement

Download asset Open asset

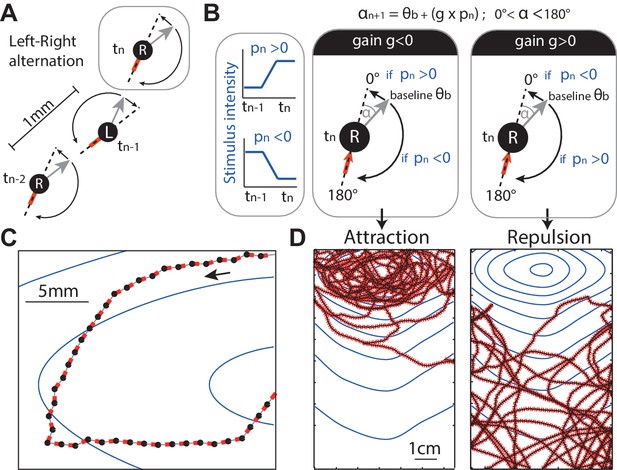
Discrete-time agent model.

(A) The agent consists of an oriented point (black dot) from which the odour concentration is sampled, the grey arrow indicates its orientation and the red line indicates the motion trail. At each time step, the agent performs a rotation ( $0 \leq α \leq 180$ deg) on the spot alternating between left and right rotations (‘L’ and ‘R’) so as to set a new orientation (grey arrow), and then moves forward by 1 mm. (B) In the absence of stimulation, the extent of this rotation is set according to a constant baseline $θ_{B}$ (typically $θ_{B}$ =10 deg), which is alternated between L and R causing movement in a zig-zag fashion. In the presence of stimulation, the extent of the rotation (e.g., towards the right) is modulated by the change of stimulus intensity (blue line, $p_{n - 1}$ ) perceived between the previous $t_{n - 1}$ and current $t_{n}$ position. The modulation is simplified down to a linear constant gain $g$ ; so that the extent of the rotation (here towards the right) is: $α = θ_{B} + g \times p_{n - 1}$ . As a result, when $g < 0$ , an increase in stimulus intensity perceived ( $p_{n - 1} > 0$ ) would decrease the extent of the rotation towards 0 degrees (i.e. the agent goes straight), whereas a decrease in stimulus intensity perceived ( $p_{n - 1} < 0$ ), would increase the rotation up towards 180 degrees (i.e. agent makes a U-turn). Effectively, a negative gain ( $g < 0$ ) yields attraction towards higher stimulus intensity. Inversely, a positive gain ( $g > 0$ ) yields aversion (D) ( $g = 0$ results in neither). (C,D) Section path examples from agent simulation in an odour gradient, with line colours as in (A). The underlying dark continuous line indicates the overall path taken by the agent. The blue lines indicate the isoclines of the odour concentration.

https://doi.org/10.7554/eLife.15504.006

Figure 3—figure supplement 1

Download asset Open asset

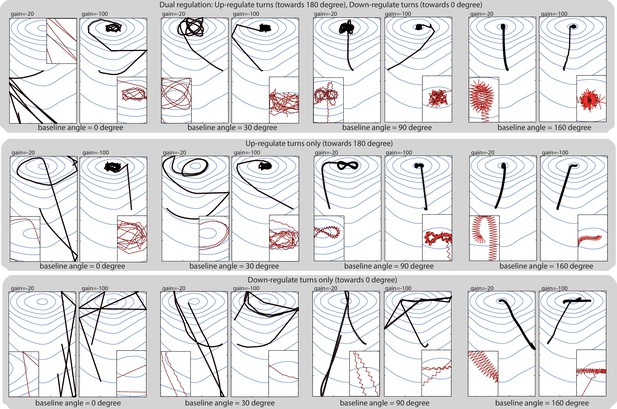
Model’s robustness to change in baseline angle.

The baseline angle corresponds to the extent of the spontaneous lateral oscillatory turns effected in the absence of sensory stimulation. In our abstract model, the baseline is set to 10 degrees to fit roughly the data observed in larvae, but taxis emerges even for extreme values such as 160 degrees, showing that the principle behind our model (i.e. sensory modulation of continuous lateral oscillation) provides a robust way of achieving taxis. Up-regulating turn towards 180 degrees (i.e. when a negative transient is perceived) appears more important than down-regulating turn towards 0 degrees (i.e. when a positive transient is perceived); however, taxis still emerges by only down-regulating turns when the baseline angle is large and leaves enough range for modulation. We have reasons to think that larvae achieve taxis by dual regulation, that is, by performing both up-regulation and down-regulation of turns (see for Discussion our supplemental text: ‘Depolarisation and hyperpolarisation rather than ON and OFF cells’).

https://doi.org/10.7554/eLife.15504.007

Figure 4

Download asset Open asset

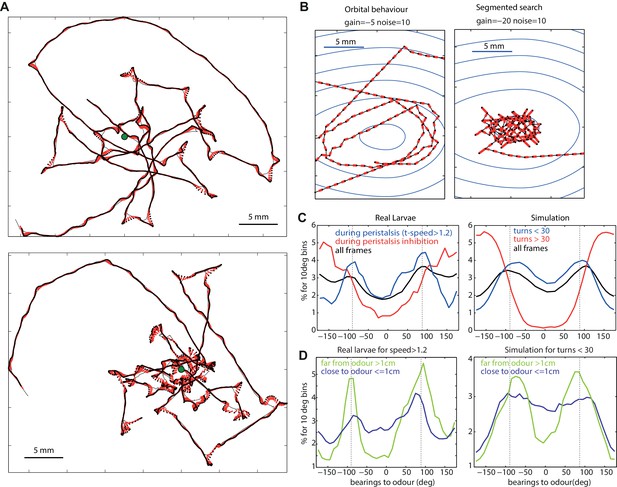
Typical path signatures for larvae and simulation.

(A,B) Example of paths. (C,D) Distributions of bearings to odour. Both larvae and simulated agents tend to spend most time with the odour located on their sides (−90 and 90 degrees), orbiting the source. In both larvae and simulation, orbital behaviour is emphasized during peristalsis forward motion (turn < 30 degrees for the model) (C blue curve), and when the larvae/agent is more than 1cm away from the odour (D green curve). Crossing-over trajectories, by contrast, are constituted of regular large turns that happen mostly while the larvae/agent is heading away from the odour (C red curve) and is rather apparent when the larvae/agent is close to the odour (D blue curve).

https://doi.org/10.7554/eLife.15504.008

Figure 5

Download asset Open asset

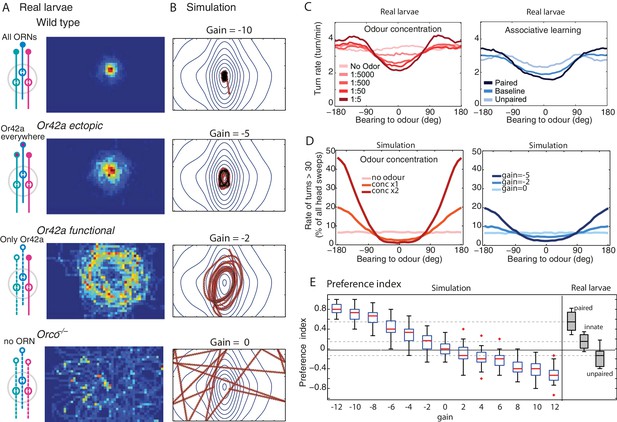
Modulation of the chemotactic response.

(A) Time occupancy spatial maps for genotypes with re-engineered peripheral olfactory circuits tested in the near-source paradigm (30 mM odour source): wild type (N = 42 flies), Or42a ectopically expressed in the 21 intact ORNs (all neuron pairs active, N = 38), Or42a single-functional ORN (one pair of neuron active, N = 37), and Orco null (anosmic flies, N = 55) adapted from Gomez-Marin et al. (2011). (B) The simulated agent can capture the patterns observed in larvae by changing $g$ , suggesting that OSN activity acts collectively to increase the turning modulation signal. (C) Effect of odour concentration and appetitive conditioning on turn-rate (larva data from Schleyer et al., 2015b). (D) In our simulation (shows mean $\pm$ std. dev.), turning events were categorised as large turns if > 30 degrees and not followed by another large turn. Changes in stimulus intensity were obtained by multiplying the gradient by a factor 0, 1 or 2. Learning was modelled as a change in gain ( $g = 0$ , $g = - 2$ or $g = - 5$ ). The same qualitative changes in turn-angle and turn-rate relative to odour bearing are observed. (E) Preference index ( $(N_{o d o u r - s i d e} - N_{o t h e r - s i d e}) / N_{t o t a l}$ ) for 30 simulated larvae after 3 min, for different gains (larva data from Schleyer et al., 2015b).

https://doi.org/10.7554/eLife.15504.009

Figure 6

Download asset Open asset

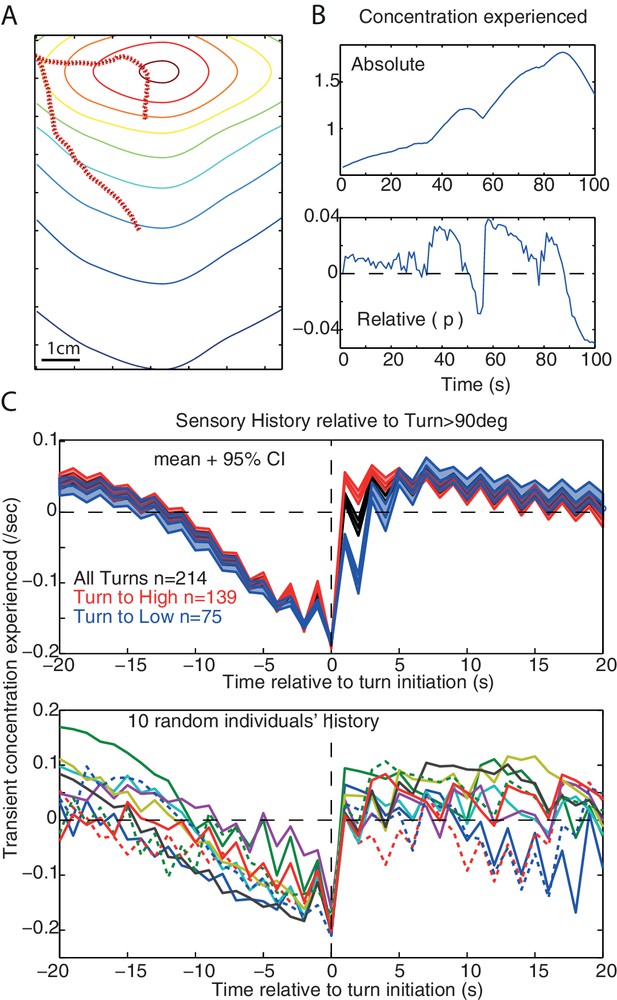
Sensory history and monotonic decrease in concentration.

(A,B) Example of simulated path and the associated sensory history given the absolute ( $s_{n}$ ) and relative ( $p_{n}$ ) odour concentration perceived. (C) Average (±95%CI) and individual’s example of the sensory history experienced before and after large turn events (>90 degrees) in our simulation, for all large turns (black), or only the large turns that result in experiencing a positive (red) or a negative $p_{n}$ (blue). A slow monotonic decrease in concentration precedes large turns even though turns are the consequence of the signal experienced during the previous step only.( $g = - 5$ , noise = 10 deg).

https://doi.org/10.7554/eLife.15504.010

Figure 7

Download asset Open asset

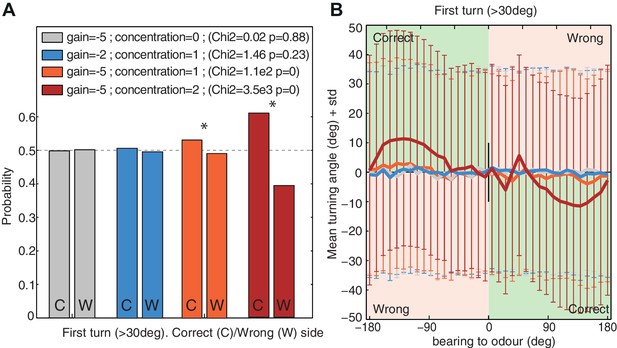
First turn bias towards the correct side.

The model's first turns were categorised as large turns (>30 degrees) that were not preceded by a large turn in the previous timestep. (A) Probability of turning to the correct side (i.e. towards the odour; 1st column ‘C’) and wrong side (second column ‘W’). Higher signals (i.e. increased concentration or stronger gain $g$ ) increase the bias. (B) Turning direction (mean ± standard deviation) given the bearing to odour. Green and red zones indicate turns towards (i.e. correct side) or away (i.e. wrong side) from the odour respectively. Noise $Z = 10$ . Time $t = 800$ . larvae ( $n > 25000$ for each group).

https://doi.org/10.7554/eLife.15504.011

Figure 8

Download asset Open asset

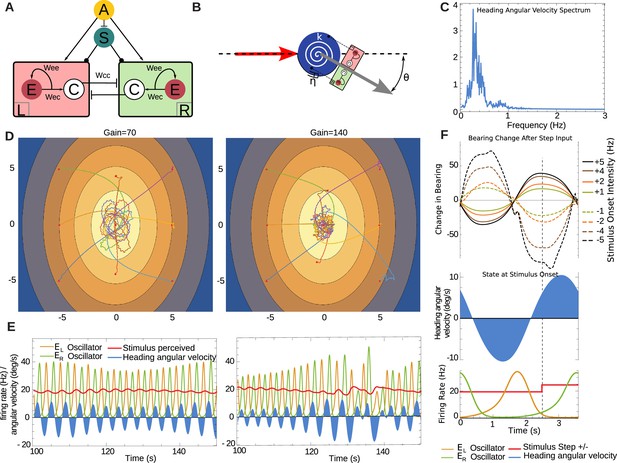
Neural model in continuous time.

(A) Central pattern generator modelled with neurons of mean firing rates (adapted from Wilson, 1999). Arrows indicate excitatory connections, a bar denotes an inhibitory connection and circle denotes a neuromodulatory connection. Cross inhibitory connections go to all neurons of the opposite compartment. The $A$ unit represents mean firing rate of an OSN, and it projects to both compartments. The $S$ unit represents a neuromodulatory neuron which modulates the half-response threshold of the $E$ and $C$ neurons to effectively imitate the effects of a slow adapting current. We denote the left and right $E$ as $E_{L}$ and $E_{R}$ respectively. (B) A torsional spring is acting on the agent heading change to represent the restoring viscoelastic forces of the larva body bends. The red arrow indicates the direction from which the agent is coming, and the grey arrow indicates its heading direction. (C) Frequency spectrum of heading velocity oscillations that are comparable to larval data. (D) Example taxis trajectories in a virtual odour gradient with different gain. (E) Sample oscillator dynamics during chemotaxis, showing $E_{L}$ and $E_{R}$ alternating, while the $A$ input as influenced zig-zag motion of the agent in the environment. Under high-gain the turns appear sharper as required. (F) Effects of unit-step perturbations on bearing angle across oscillator phase. Panels below show the simultaneous state of the heading angular velocity, an example step-up in the firing rate of $A$ and the respective state of neural bursts from $E_{L}$ and $E_{R}$ (here shown unperturbed by the step-input $A$ ).

https://doi.org/10.7554/eLife.15504.012

Figure 9

Download asset Open asset

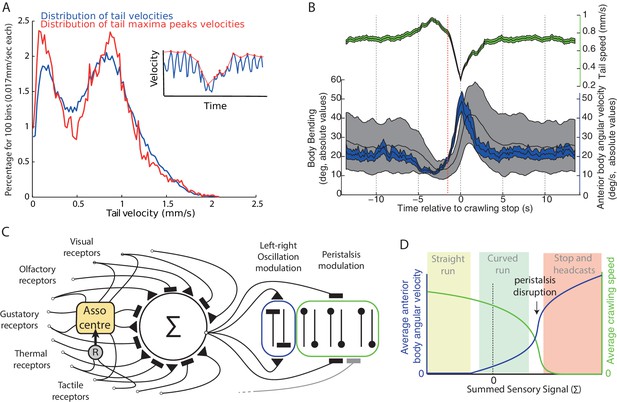
Oscillation and peristalsis modulation.

(A) Real larvae tail velocities show a bimodal distribution, with the first peak corresponding to peristalsis inhibition events. Inset illustrates the extraction of maxima peaks (red curve) of tail velocities. (B) Average (±95%CI) of the tail velocities (green) and absolute values for the anterior body angular velocity (blue) and body bending (black) displayed before and after peristalsis inhibition events (aligned at t = 0, when tail speed dropped to a minimum). Red line highlights that average tail speed velocity (green) starts dropping before the occurrence of a large increase in body bending (black) or anterior body angular velocity (blue). This suggests that tail speed is not a mere physical consequence of a large turning event. (C) Conceptual scheme illustrating our overall view: all modalities, innate and learnt, are integrated at the zone of convergence. The summed signal is sent to both the neural oscillator mediating turning of the anterior body (blue), and to neurons mediating peristalsis inhibition (green). Associative center (Asso center), such as the mushroom body, where signal weightings can be modulated given the co-activation of a reinforcer neuron (R). Note that our scheme allows for sensory inputs to bypass the zone of convergence, and send their signals directly onto local control of the oscillator and/or the peristalsis motion. (D) Qualitative depiction of how apparently distinct behaviours could emerge from a continuous modulation signal. Growing signal strength increases anterior body angular velocity (blue) and inhibits crawling speed (green) simultaneously. If the signal is sufficiently strong peristalsis disruption happens (arrow), leading to an abrupt drop of tail speed velocities. The relaxing of the peristaltic synchronous left-right body contraction enhances the reaction to the thoracic left-right asynchronous oscillatory contraction, thus resulting in sharp increase in head sweep amplitude. Peristalsis spontaneously resumes when the sensory command lowers below peristalsis disruption threshold. The combinations of these two parameters (blue and green) can lead to the emergence of straight runs (light green area), curved runs (light blue area) and the stop and head-casts (light red area) behaviours as observed in larvae.

https://doi.org/10.7554/eLife.15504.013

Tables

Table 1

CPG model parameter set and initial conditions. $M (x, y)$ is the multinomial distribution of Equation 25.

https://doi.org/10.7554/eLife.15504.014

Parameters
$W_{c c}, W_{e c}$	4
$W_{c e}$	1/10
$W_{e e}$	3
$b_{T}$	19
$τ$	1/10
$m$	$10^{2}$
$n$	$2$
$c$	$10^{3}$
$ρ$	1/5
$ζ$	1/2
$k$	1

Initial Conditions
$C_{L} (t \leq 0), C_{R} (t \leq 0)$	0
$E_{L} (t \leq 0)$	80
$E_{R} (t \leq 0)$	20
$H_{E L} (t \leq 0)$	0
$H_{E R} (t \leq 0)$	0
$H_{C L} (t \leq 0)$	0
$H_{C R} (t \leq 0)$	0
$θ (t \leq 0)$	0
$B (t \leq 0)$	0
$A (t \leq 0)$	$b_{T}$
$g (t \leq 0)$	$6 + {(9 A (0) / 100)}^{2}$
$τ_{H} (t \leq 0)$	$35 / (1 + 0.04 A {(0)}^{2})$
$C (t \leq 0)$	$M (x (0), y (0))$

Download links

A two-part list of links to download the article, or parts of the article, in various formats.

Downloads (link to download the article as PDF)

Open citations (links to open the citations from this article in various online reference manager services)

Mendeley

Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)

Antoine Wystrach
Konstantinos Lagogiannis
Barbara Webb

(2016)

Continuous lateral oscillations as a core mechanism for taxis in Drosophila larvae

eLife 5:e15504.

https://doi.org/10.7554/eLife.15504

Sign up for email alerts

Privacy notice