Community-level cohesion without cooperation
- Harvard University, United States
Figures
Figure 1
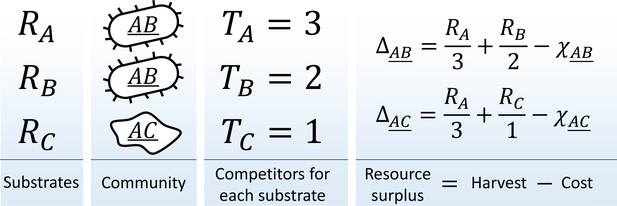
The metagenome partitioning model.
Organisms are defined by the pathways they carry. The benefit from each substrate is equally partitioned among all organisms who can use it, and population growth/death of each species is determined by the resource surplus it experiences.
Figure 2
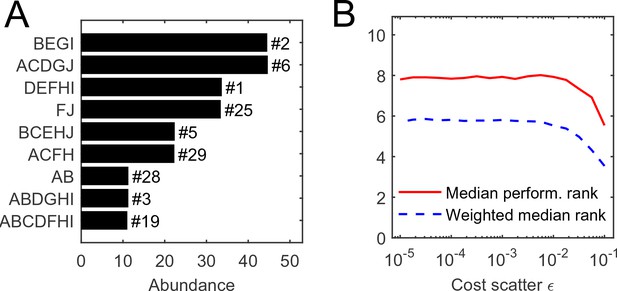
The individual performance rank of a species (its cost per pathway) is predictive of its survival and abundance in a community.
(A) Community equilibrium for substrates with abundance and one particular random realization of organism costs with scatter . Species are ordered by abundance and labeled by the pathways they carry. Also indicated is the individual performance rank; all surviving species were within the top 30 (out of 1023). (B) The median individual performance rank of survivors, weighted (dashed) or not weighted (solid) by abundance. Curves show mean over 100 random communities for each value of cost scatter ; the standard deviation across 100 instances is stable at approximately 40% of the mean for both curves, independently of (not shown to reduce clutter).
Figure 3
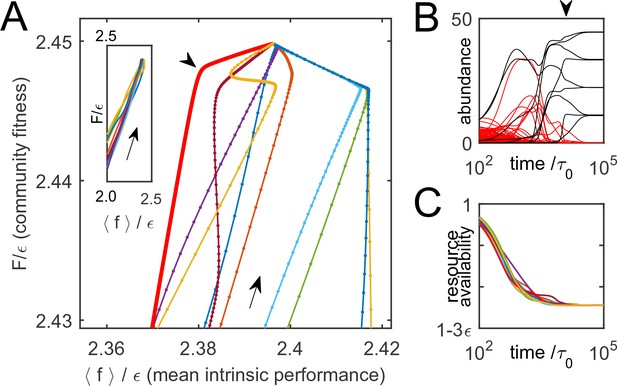
Community dynamics maximize a global objective function.
(A) 10 trajectories of an example system, starting from random initial conditions and converging to the equilibrium depicted in Figure 2A. Direction of dynamics indicated by arrows. Far from equilibrium, mean intrinsic performance of members (weighted by abundance) and the community-level function increase together (inset; data aspect ratio as in the main panel). Close to equilibrium, intrinsic performance loses relevance. (B) Time traces of species’ abundance for one community trajectory (thick red line in A). Arrowheads in panels A and B indicate matching time points. Species that eventually go extinct shown in red; many enjoy transient success. (C) The complex dynamics of panel B is driven by the simple objective to efficiently deplete all substrates simultaneously, encoded in . Shown is mean availability of the 10 substrates, for each trajectory of panel A.
Figure 4
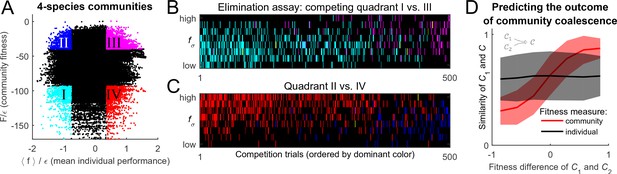
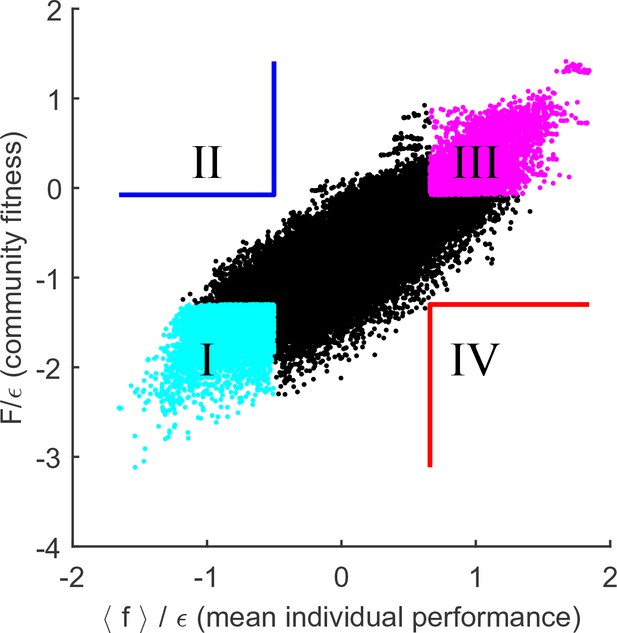
Community fitness is more predictive of competition outcome than the intrinsic performance of its members.
(A) Community fitness vs mean intrinsic performance of its members, measured in units of cost scatter , for 104,006 communities with four species (see text). Communities in which both characteristics are in the top or bottom 10% are highlighted. (B) Elimination assay competing quadrants I (cyan) vs III (magenta). Five hundred randomly drawn community pairs (columns) were jointly equilibrated, with up to eight species each time (rows; ordered by ). For each species that went extinct during equilibration, the corresponding cell in the table is colored by the species’ provenance. As expected, most eliminated species were from the less fit cyan communities (there are more cyan cells than magenta). These species also had lower (most colored cells are in the lower half of the table). (C) Same, competing quadrants II (blue) vs IV (red). The dominant color is now red: most eliminated species were from red communities, and went extinct despite having higher (most colored cells are in the upper half of the table). Columns ordered by dominant color. (D) Community similarity for a coalescence event depicted in the cartoon (inset), computed for random community pairs, as a function of fitness difference between competing communities. Fitness difference scaled to the maximum of 1 so both fitness measures can be shown in same axes. Shown is binned mean (7 bins) over communities with similar fitness difference (solid line) standard deviation (shaded).
Figure 5
Cost scatter tunes the magnitude of community cohesion.
Same as Figure 4A, for larger . Increasing the scatter of intrinsic costs reduces the relative importance of environment in determining the performance ranking of species. As a result, collective fitness of a community and the mean individual performance of its members remain strongly coupled. Defining quadrants as in Figure 4A leaves the blue and red quadrants empty.
Additional files
-
Supplementary file 1
Technical details, numerical procedures, and relation to the model of MacArthur.
- https://doi.org/10.7554/eLife.15747.008
-
Supplementary file 2
MatLab scripts reproducing all figures (optional data files with pre-computed simulation results included for faster figure plotting).
- https://doi.org/10.7554/eLife.15747.009
Download links
A two-part list of links to download the article, or parts of the article, in various formats.
Downloads (link to download the article as PDF)
Open citations (links to open the citations from this article in various online reference manager services)
Cite this article (links to download the citations from this article in formats compatible with various reference manager tools)
Community-level cohesion without cooperation
eLife 5:e15747.
https://doi.org/10.7554/eLife.15747
